16.1 屏幕到投影窗口的变换
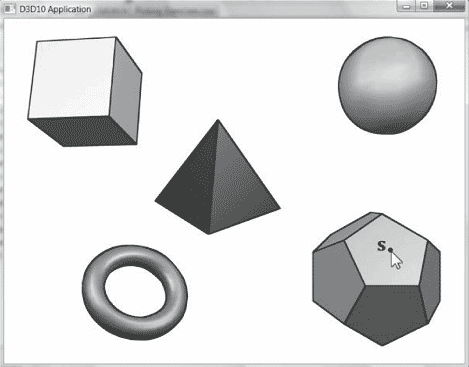
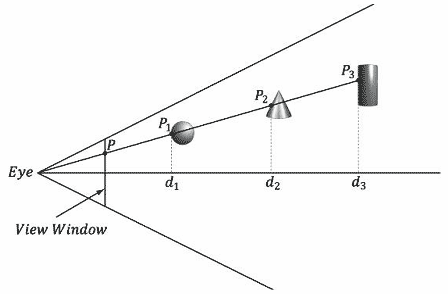
在本章中,我们要讨论如何对用户使用鼠标拾取的3D物体或图元进行测定(参见图16.1)。换言之,当给定鼠标的2D屏幕坐标时,我们是否能够推断出位于该投影点上的3D物体?从某种意义上说,我们要解决这一问题就必须做一些与之前相反的工作;也就是说,我们通常都是从3D空间变换到屏幕空间,而这里我们要从屏幕空间变换回3D空间。当然,我们还必须解决另外一个小问题:不存在一个与2D屏幕点唯一对应的3D点(即,可以有任意多个3D点投影在同一个2D点上——参见图16.2)。所以,在测定实际拾取的物体时存在一些不确定性。不过,这不是什么大问题,因为通常与摄像机距离最近的物体就是我们实际拾取的物体。
考虑图16.3所示的视域体。这里,p是屏幕坐标s在投影窗口上的位置。现在,如果我们从观察点引出一条穿过点p的拾取射线,那该射线将会与所有投影到点p上的物体相交,在本例中与射线相交的是圆柱体。所以,我们的实现思路是:只要我们计算出一条拾取射线,就可以遍历场景中的每个物体,测试物体是否与该射线相交。与射线相交的物体就是被用户选中的物体。前面提到,射线可能会与场景中的多个物体相交(当然,也有可能不会与任何物体相交)。如果我们沿着射线的路径观察物体,那么就会发现它们具有不同的深度值。既然这样,我们就可以将与摄像机距离最近的相交物体作为最终的拾取物体。
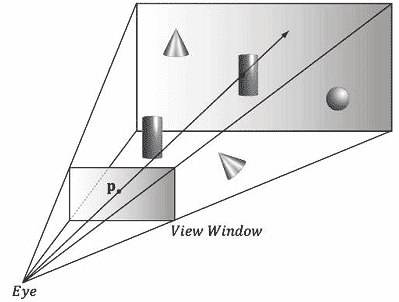
注意,投影点p是屏幕坐标s在投影窗口上的位置。学习目标学习如何实现拾取算法,理解拾取算法的工作原理。我们将拾取算法分解为如下4个步骤:
1.给定屏幕坐标s,求出它在投影窗口上的对应点p。
2.在观察空间中计算拾取射线。该射线从观察空间的原点射出,并穿过点p。
3.把拾取射线和模型变换到同一个空间,测试模型是否与拾取射线相交。
4.确定与射线相交的物体。(与摄像机距离)最近的物体就是用户拾取的屏幕物体。
第一步是把单击的屏幕坐标变换为规范化设备坐标(参见5.6.3.3节)。回顾前文,视口矩阵(viewport matrix)可以把顶点从NDC空间变换到屏幕空间:
\[{\bf{M}} = \left[ {\begin{array}{*{20}{c}}{\frac{{Width}}{2}}&0&0&0\\0&{ - \frac{{Height}}{2}}&0&0\\0&0&{MaxDepth - MinDepth}&0\\{TopLeftX + \frac{{Width}}{2}}&{TopLeftY + \frac{{Height}}{2}}&{MinDepth}&1\end{array}} \right]\]
视口矩阵中的这些变量由D3D11_VIEWPORT结构体指定:
typedef struct D3D11_VIEWPORT {
FLOAT TopLeftX;
FLOAT TopLeftY;
FLOA Width;
FLOA Height;
FLOAT MinDepth;
FLOAT MaxDepth;
} D3D11_VIEWPORT;
对于游戏来说,视口通常是整个后台缓冲区,深度缓冲区的取值范围是[0,1]。所以,该结构体的成员应分别设置为:TopLeftX = 0、TopLeftY = 0、MinDepth = 0,MaxDepth = 1,Width = w,Height = ℎ,其中w和ℎ是后台缓冲区的宽度和高度。此时的视口矩阵可简化为:
\[{\bf{M}} = \left[ {\begin{array}{*{20}{c}}{\frac{w}{2}}&0&0&0\\0&{ - \frac{h}{2}}&0&0\\0&0&1&0\\{\frac{w}{2}}&{\frac{h}{2}}&0&1\end{array}} \right]\]
现在,设pndc = (xndc,yndc,zndc,1)是NDC空间中的一个点(即,−1≤xndc≤1、−1≤yndc≤1、0≤zndc≤1)。将pndc变换到屏幕空间后的结果为:
\[\left[ {{x_{ndc}},{y_{ndc}},{z_{ndc}},1} \right]\left[ {\begin{array}{*{20}{c}}{\frac{w}{2}}&0&0&0\\0&{ - \frac{h}{2}}&0&0\\0&0&1&0\\{\frac{w}{2}}&{\frac{h}{2}}&0&1\end{array}} \right] = \left[ {\frac{{{x_{ndc}}w + w}}{2},\frac{{ - {y_{ndc}}h + h}}{2},{z_{ndc}},1} \right]\]
坐标zndc只由深度缓冲区使用。在拾取中,我们不需要考虑任何深度坐标。2D屏幕坐标ps = (xs,ys)仅与pndc变换后的x、y坐标有对应关系:
\[\begin{array}{l}{x_s} = \frac{{{x_{ndc}}w + w}}{2}\\{y_s} = \frac{{ - {y_{ndc}}h + h}}{2}\end{array}\]
上述方程说明,只要给定规范化设备坐标pndc和视口大小,我们就可以得到屏幕坐标ps。不过,在拾取过程中我们最初得到的是屏幕坐标ps和视口大小,想要求出的是pndc。所以,由上述方程解得:
\[\begin{array}{l}{x_{ndc}} = \frac{{2{x_s}}}{w} - 1\\{y_{ndc}} = - \frac{{2{y_s}}}{h} + 1\end{array}\]
我们现在有了NDC空间中的屏幕坐标。不过,在计算拾取射线时,我们实际想要的是观察空间中的屏幕坐标。回顾5.6.3.3节,我们通过将x坐标除以横纵比r,使投影点从观察空间变换到NDC空间:
\[\begin{array}{l} - r \le x' \le r\\ - 1 \le \frac{{x'}}{r} \ge 1\end{array}\]
那么,要回到观察空间,我们只需要将NDC空间中的x坐标乘以横纵比r。现在,观察空间中的屏幕坐标为:
\[\begin{array}{l}{x_v} = r\left( {\frac{{2{x_s}}}{w} - 1} \right)\\{y_v} = - \frac{{2{y_s}}}{h} + 1\end{array}\]
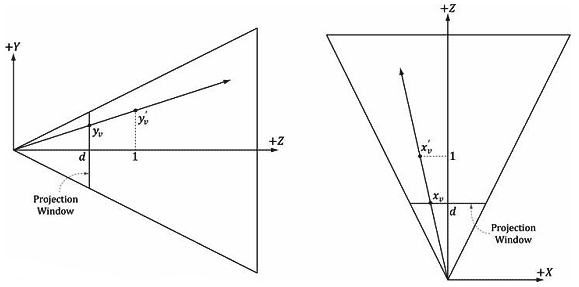
注意:观察空间和NDC空间中的y坐标相同。这是因为我们把观察空间中的投影窗口高度限定在了[−1,1] 区间内。现在回顾5.6.3.1节,投影窗口与原点的距离为d = cot(α/2) ,其中α为垂直视域角。这样我们可以引出一条穿过投影窗口上的点(xv,yv,d)的拾取射线。不过,这需要我们计算d = cot(α/2) 。图16.4给出了一种更简单的方法:
\[\begin{array}{l}{x_v}^\prime = \frac{{{x_v}}}{d} = \frac{{{x_v}}}{{\cos \frac{\alpha }{2}}} = {x_v}\tan \frac{\alpha }{2} = \left( {\frac{{2{x_s}}}{w} - 1} \right)r\tan \frac{\alpha }{2}\\{y_v}^\prime = \frac{{{y_v}}}{d} = \frac{{{y_v}}}{{\cos \frac{\alpha }{2}}} = {y_v}\tan \frac{\alpha }{2} = \left( { - \frac{{2{y_s}}}{h} + 1} \right)\tan \frac{\alpha }{2}\end{array}\]
回忆一下,在投影矩阵中\({{\bf{P}}_{00}}{\rm{ = }}\frac{1}{{r\tan \frac{\alpha }{2}}}\)和\({{\bf{P}}_{11}}{\rm{ = }}\frac{1}{{\tan \frac{\alpha }{2}}}\)。我们可以将上述方程改写为:
\[\begin{array}{l}{x_v}^\prime = \left( {\frac{{2{x_s}}}{w} - 1} \right)/{\bf{P}}{}_{00}\\{y_v}^\prime = \left( { - \frac{{2{y_s}}}{h} + 1} \right)/{{\bf{P}}_{11}}\end{array}\]
这样,我们可以引出一条穿过点(xvʹ , yvʹ ,1)的拾取射线,它与穿过点(xv , yv ,d)的拾取射线是同一条射线。下面给出了在观察空间中计算拾取射线的代码:
void PickingApp::pick(int sx, int sy)
{
XMMATRIX P = mCam.Proj();
// 在视空间中计算拾取射线
float vx = (+2.0f*sx/mClientWidth - 1.0f)/P(0,0);
float vy = (-2.0f*sy/mClientHeight + 1.0f)/P(1,1);
// 视空间中的射线定义
XMVECTOR rayOrigin = XMVectorSet(0.0f, 0.0f, 0.0f,1.0f);
XMVECTOR rayDir = XMVectorSet (vx, vy, 1.0f,0.0f);
注意,该射线的起点是观察空间的原点,因为观察点位于观察空间的原点上。
文件下载(已下载 1282 次)发布时间:2014/8/16 下午8:27:42 阅读次数:5195
