第四章 机械能参考资料

1．机械能转化与守恒定律是怎样被发现的

1755年至1807年间，瑞士物理学家欧拉（L. Euler）提出了与速度和重力有关的“力函数”、“速度势”概念，法国物理学家拉格朗日（J.L.Lagrange）则给出了“重力势函数”；1807年英国著名物理学家托马斯•扬（T.Young）在《自然哲学与机械技术》讲义中，最先提出了能量的概念，指出产生运动所需要的功等于“物体的质量和速度的二次方积”；1829年，法国物理学家科里奥利建议将托马斯•扬提出的“能量”乘以$\frac{1}{2}$，标为动能，这很快得到了公认；同年，物理学家庞斯莱明确提出了动能定理。

1834年至1835年间，爱尔兰数学物理学家哈密顿（W.R.Hamilton）提出了哈密顿原理，阐明了保守力场中动能和势能的转化及它们的总和保持不变。这就是机械能转化与守恒定律。

（摘自上海科技出版社出版的《普通高中实验教科书物理2》）

2．著名科学家谈“不变性”和“守恒律”

自然过程千变万化，却总按一定的规律进行，科学就是要在那万般变化的自然界里找出“不变性”，即各种各样的“守恒律”。诺贝尔物理学奖获得者，德国物理学家劳厄（M.von Laue，1879～1960）曾经指出：“物理学的任务是要发现普遍的自然规律，而且又因为这样的规律性的最简单的形式之一，是它表明了某神物理量的不变性，所以对于守恒量的寻找不仅是合理的，而且也是极为重要的研究方向。”

诺贝尔物理学奖获得者，美国物理学家费恩曼（R.P.Feynman，1918～1988）曾说过：“有一个事实，或如果你愿意，也可以说一条定律，支配着至今所知的一切自然现象……。这条定律称作能量守恒。它指出有某一个量，我们称它为能量，在自然界经历的多种多样的变化中它不变化。那是一个最为抽象的概念……”

3．涉及弹性势能的机械能守恒定律的应用

弹性势能的表达式为E_p＝$\frac{1}{2}$kx²，即弹簧的弹性势能等于它的劲度系数跟它的伸长（或压缩）的平方的乘积的一半。弹性势能的零势能点是弹簧的未形变时的端点位置，无论弹簧被压缩还是拉长，其弹性势能总是增大的。

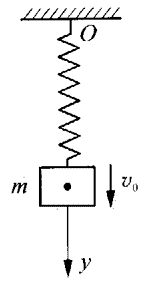
如图4-4所示，一劲度系数为k的轻弹簧，上端固定于O点，下端挂一质量为m的物体。先将物体提起，使弹簧处于自由状态。然后给予物体以向下的速度v₀，忽略空气阻力，求物体所能下降的最大距离。

如果以地球、弹簧和物体组成的系统为研究对象，因只有作为保守力的重力和弹力作功，系统的机械能守恒。取弹簧处于自由状态时物体的位置A为弹性势能和重力势能的零点。考虑到物体下降到最大距离y时，其速度为零。于是有

$\frac{1}{2}$mv₀²＝$\frac{1}{2}$ky²－mgy

解得

y＝$\frac{mg}{k}(1+\sqrt{1+\frac{k{v}_0^2}{m{g}^2}})$。

（以上摘自赵凯华等著<新概念高中物理读本•第一册》）

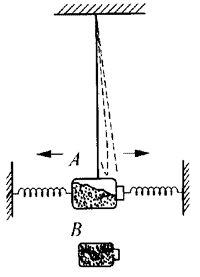
4．内摩擦导致机械能不守恒的演示实验

如图4-5所示，取一个塑料瓶A，内部盛有$\frac{3}{4}$的水，将其悬挂起来，瓶的两边用固定的弹簧系住，做成一个振子，使其偏离平衡位置后放手，发生振动。发现瓶内水在不停晃动，振动的振幅迅速递减下来，水的内摩擦使机械能损耗了。如果更换一个塑料瓶B，它比A小，使水恰好能充满瓶子（水和瓶的质量与A相同），使其同样偏离平衡位置后发生振动，发现振动延续时间明显增大，此时可以认为机械能是守恒的。

发布时间：2013/12/31 上午8:46:47  阅读次数：1676