第四章B 机械能守恒定律的应用教学建议

（一）学习目标

1．熟练掌握机械能守恒定律，以合理的步骤运用机械能守恒定律解决简单的实际问题。

2．通过对若干实际问题的讨论，经历建模、状态分析与综合运用相关知识的过程。

3．领略机械能守恒定律在解决水力资源利用、列车编组等实际问题中的重要应用价值。

（二）重点和难点

本节的重点是以正确的步骤运用机械能守恒定律，难点是建立物理模型、状态分析和寻找物理量之间的关系。

（三）教学建议

本节从荡船、瀑布情景中引入，它们包含了机械能守恒定律应用的内容，一开始就进入了如何应用、如何建模的问题。接着课本指出了解题的要点和步骤，只有结合实例才能认识这些步骤是必要的、重要的。

课本所举的3个示例中，示例1驼峰编组是单个物体的应用，后2个示例是2个物体组成的系统的应用。示例3中2个物体速度不同，要联系角速度、线速度关系问题（在基础型课程中周期运动先于机械能教学，因此是有学习基础的）。最后还可以回到本节引入的情景问题作一些分析。

本节建议安排2课时，第1课时学示例1、示例2，第2课时学示例3及练习部分的示例等。

1．关于引入部分的说明

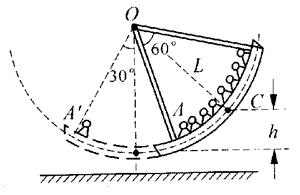
课本图4-7中的荡船，在运用机械能守恒定律时，首先要对它进行抽象，将船看作为重心在C，绳长为L的一个摆球。若摆动时重心最大升起高度为h（如图4 -2），则至最低点每个人（包括船体）的最大速度v＝$\sqrt{2gh}$，如果船身所对应圆心角为60°，则船左侧那个人A的速度最大位置是在他偏离竖直方向30°的Aʹ处，不是在最低点。

课本图4-8所示的“神龙瀑”，欲求其每秒钟获得的动能，也是一个建模的过程。这里不计阻力，也不计算初速度，因此水看作是自由下落的，水的每秒钟具有的动能，是由每秒钟变化的势能转化而来的，而每秒变化的势能又是由每秒钟流出水的质量、高度和重力加速度g所决定的。由水的流量可知每秒流出水的质量为Δm＝18.13×10³kg，于是ΔE_k＝－ΔE_p＝mgh＝18.13×10³×10×56J＝1.02×10⁷J，如果这些水全部用来发电，可提供大约10⁴kW的功率。

在课开始时这两个问题仅仅用来引出问题，具体解决可留在课的最后。

2．关于课本第46页示例1的说明

“驼峰”是铁路编组站用来解体和组编货物列车的主要设施，最早建于1876年德国。19世纪90年代开始，一些铁路发达国家纷纷修建驼峰。1924年首先使用安装减速器的机械化驼峰，现在又建起运用计算机控制的自动化驼峰。课本中图4 – 9（c）是一个侧视图，它只是示意图，实际上峰顶后面的第一斜坡其陡度不会这么大，示例1中算出的峰高仅3.1m，实际上由于滑行轨道上都安装有减速器，因此驼峰高度会高许多，这样可以缩短溜放的时间。

3．关于课本第47页示例2的教学建议

本题是由2个物体组成的物体系的机械守恒定律的应用。在分析本题时应指出，竖直槽壁与水平槽的转角处是圆弧形的，A球不会在此发生撞击和弹跳。

学完示例2，可让学生做自主活动（课本第47页图4-11），它的类型与示例2是相似的，但在解题方法上有繁简之分。最简单的解法是，当2m球转过180°后，系统势能变化是减少mg2R，这时四个球的速度大小是相同的，均为v，则2mgR＝$\frac{1}{2}$5mv²，v＝$\sqrt{\frac{4}{5}gR}$。

4．关于课本第47页示例3的教学建议

课本采用“势能的总减少量等于动能的总增加量”来求解，也可以采用机械能总量保持不变的办法来求解，设课本中图4-12为第1状态，课本图4-13为第2状态。求解小题（1）时取第2状态的A位置为零势能参考平面，则各状态的动能和势能可写作：

第1状态E_k1＝E_k1A＋E_k1B＝0，E_p1＝E_p1A＋E_p1B＝mgr＋mg$\frac{r}{2}$。

第2状态E_k2＝$\frac{1}{2}$mv_A2²＋$\frac{1}{2}$mv_B2²，E_p2＝E_p2A＋E_p2B＝0＋mgr，其中v_A2＝2v_B2。

根据机械能守恒定律有

E_k1＋E_p1＝E_k2＋E_p2，

mgr＋mg$\frac{r}{2}$＝$\frac{1}{2}$mv_A2²＋$\frac{1}{2}$m（v_A2/2 ）²＋mgr，

同样解得

v_A2＝$\sqrt{\frac{4}{5}gR}$。

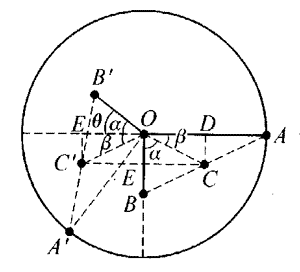
本示例的小题（2）也可以有另一种解答方法，如图4-3所示，在初始状态，A、B两球的重心在AB连线的中点C处，设∠COB＝α，∠COD为β，在转动过程中C相对于AB的位置是不变的。当盘转动后向左边升起最大高度时，重心位置应达Cʹ，Cʹ与C完全对称，即高度应相同，这时系统的动能又全部转化为重力势能。这时两球分别处在Aʹ和Bʹ位置。设OBʹ与水平线的夹角为θ，也就是OAʹ偏过竖直方向的夹角，即所求的θ角。这时α角，β角均到达左边。由几何关系可知：

tanβ＝$\frac{r}{4}$/$\frac{r}{2}$＝$\frac{1}{2}$，β＝26.56°。

tanα＝$\frac{r}{2}$ /$\frac{r}{4}$＝2，α＝63.45°。

θ＝α－β＝37°。

得到的答案与课本上是一致的。这里所用的方法是求等效重心位置变化。

（四）作业说明

本节的练习部分中共有14题，如果安排2课时教学，第1课时课内可使用第1至第3题，课外使用第4、5、6及8、9题；第2课时可使用其余6题，其中第14题可机动处理。

参考答案

A组

1．BD

2．2gL²/v²

3．v_A＝$\sqrt{\frac{2}{5}gh}$，v_B＝2$\sqrt{\frac{2}{5}gh}$

4．H＝0.45m

5．2$\sqrt{gh}$

6．不计能量损失MgH应与mgh相当，因M≫m，所以h≫H，故跳得很高

7．BCD

B组

8．m下降高度h＝$\frac{s}{\cos \theta }$－stanθ，m至最低点时速度为零，则mgh＝$\frac{1}{2}$Mv²，v＝$\sqrt{\frac{2m}{M}(\frac{1-\sin \theta }{\cos \theta })gs}$，如果存在滑轮b，则M做往复运动，m上下运动

9．D

10．$\sqrt{\frac{26}{7}gl}$

11．v_B＝$\frac{2v_A}{\sqrt{3}}$，mgh＝$\frac{1}{2}$mv_A²＋$\frac{1}{2}$（2m$\frac{4}{3}$v_A²），v_A＝$\sqrt{\frac{6}{11}gh}$

12．v＝$\sqrt{\frac{4Mg\pi nr}{M+6m\frac{l^2}{r^2}}}$

13．S₁v₁＝S₂v₂，v₂＝v₁$\frac{S_1}{S_2}$，mgh＝$\frac{1}{2}$mv₁²－$\frac{1}{2}$mv₂²，得v₁＝$\sqrt{\frac{2gh{S}_2^2}{S_2^2-S_1^2}}$

发布时间：2013/12/30 上午10:57:56  阅读次数：1546