第三章 牛顿运动定律参考资料
1.关于摩擦力
(1)关于摩擦力产生的机理
摩擦力来源于两个接触表面之间相互的力的作用,一个固体表面,用肉眼看是光滑的,但放大来看却是凹凸不平,好像布满千峰万谷。车床上车制的金属表面,峰高可达5×10-6m,经过仔细研磨,峰高可减至0.1×10-6m,但相对于原子尺度仍然是很大的,所以两个物体接触时,真正接触的只是表面上的峰点。在这些真正的接触区域内,两个接触表面(图3-9中的ΔAr)的原子非常接近,原子间有强烈的相互作用力。这些真正接触的区域称为粘结点。上图表示表面间的接触和粘结点的形成情形。在其他区域,两个表面的原子之间距离较大,从几个埃到几十个埃[1埃(Å)=10-10m]。这些相距较远的表面原子之间也有很弱的相互作用力,但可忽略不计,粘结点面积之和是真正的接触面积A,它比表观接触面积A小得多。
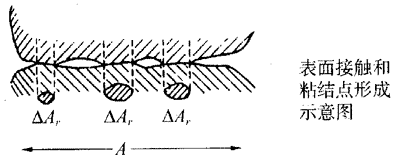
要使这样接触的两个表面发生相对滑动,势必以剪切方式破坏所有的粘结点。平行于接触表面使粘结点破坏所需要的剪切力,就等于摩擦力,如果粘结点的平均剪切强度为τ,则摩擦力为:
F=τAr。
机械加工后的金属表面布满峰和谷,两个表面在接触初期实际上只是点接触,在法向压力FN的作用下,这些点的载荷很大,使凸出部分发生弹塑性变形,从而使接触面积增大,形成图中所示的粘结点。坚硬的材料较难变形,即发生等量的变形需要更大的载荷,所以真正的接触面积A,与法向压力FN成正比,而与材料的硬度H成反比。这里所说的硬度H是指用压入法测定的硬度。理论分析表明,真正的接触面积Ar以近似地表示为:
Ar=FN/H。
根据动摩擦因数的定义,从式(3)和式(4)可求得动摩擦因数μ:
μ=F/FN=τ/H。
这说明动摩擦因数是同接触表面硬度和粘结点的抗剪强庋有关的材料常数,而同法向压力、表观接触面积和滑动速度等因素无关。两个接触物体的材料,如果一个较硬,另一个较软,则粘结点的剪切破坏将发生在材料较软的一侧,因此,动摩擦因数决定于较软材料的抗剪强度和硬度等性能参量。
实验结果证明,对于一般机械加工的表面,动摩擦因数同表面粗糙度无关;对于很粗糙的表面,因接触面上的峰和谷交错啮合,会使动摩擦因数增大;对于非常光滑的表面,尤其是特别清洁的表面,由于真正接触面积增大和粘结点粘结强度提高,所以动摩擦因数更大,表面越光洁,动摩擦因数越大,这是和直觉不同的。
大气中的金属表面,常附有氧化物薄膜,同时还可能吸附其他物质(例如水蒸气),使表面受到沾污。这层薄膜阻碍接触表面的金属原子直接接触,降低粘结点的粘结力,使动摩擦因数减小,在大气中,金属间的动摩擦因数一般均小于1,例如钛对钛的动摩擦因数μ为0.45~0.65,对于少数在大气中稳定的软金属(如铟),动摩擦因数可高达1.5~2.0。
将金属放在10-5~10-6毫米汞柱(1毫米汞柱=133.322Pa)的真空中加热到一定温度,并保持一段时间,除去表面沾污,冷却后测定动摩擦因数μ可达5~6。非常清洁的表面互相接触并受到一定的压力,甚至发生粘连,不能滑动,在工业生产中把这种现象通俗地称为咬卡。铁在发生粘连时,粘结点的强度可达63千克力/毫米2(1千克力=9.80665N),约为铁本体的强度,这又证明摩擦力确是来源于接触表面原子之间的相互力学作用。
有两种常见的摩擦特低的情况:一是在高速滑动时利用流体动力润滑,使相对滑动的两个表面被一层完整的流体膜所分隔,摩擦因数通常是0.001~0.003;另一个是利用滚动代替滑动,例如,滚珠轴承的滚动摩擦因数一般在0.002~0.005范围之内。
(摘自《中国大百科全书,力学卷》)
(2)关于滑动摩擦力通常与接触面积无关的解释
对于两个给定表面,滑动摩擦实际上与接触表面面积的大小无关,对这个事实也许有人觉得奇怪。按照目前较流行的一种理论认为,这是因为实际接触面积是属于原子尺度的,它只占总的几何接触面积的一个极微小的部分,而摩擦力的出现是由子在原子接触的这些微小区域内原子之间的相互作用力,原子接触面积占几何接触面积的比例,正比于法向力除以几何接触面积,因此,当法向力增大一倍,原子接触面积也增大一倍,摩擦力便增大一倍,这就是摩擦力正比于正压力的原因。但是,如果几何接触面积增加一倍,而法向力保持不变,则原子接触面积占几何接触面积的比例减小一半,即原子接触面积的实际面积不变,因而摩擦力也不变,对于非刚性的物体,例如汽车轮胎等,摩擦力的情况更为复杂。
(3)关于静摩擦力和静摩擦因数
设有两个物体A和B(如货物和地板)相互接触,如图3-10所示。我们推货物时如果用力F较小就推不动。A不动的事实表明,B对A的摩擦力和外力F大小相等,方向相反,这种摩擦力是在A和B相对静止但却具有相对运动趋势的情况下发生的,称为静摩擦力,当外力逐渐增大时,静摩擦力也增大。但当外力达到某一数值时,A开始移动。可见静摩擦力增到一定数值后就不能再增大了,这一数值的静摩擦力叫做最大静摩擦力,实验证明:最大静摩擦力Ff0与接触面间的正压力FN成正比,即
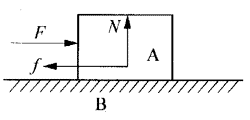
Ff0=μʹFN,
式中的μʹ叫做静摩擦因数,它由相互接触物体的质料和表面情况(如粗糙程度、干湿程度)决定,表3-1列举某些μʹ的数值。
| 相互接触的物体对 | μʹ |
| 钢—钢(干面) | 0. 15 |
| 钢—钢(涂油面) | 0. 12 |
| 金属—木材(干面) | 0.5 |
| 金属—木材(涂油面) | 0.1 |
| 金属—皮带(干面) | 0. 56 |
必须注意,静摩擦力的大小由外力的大小决定,可随外力的增大取0到Ff0之间的各个数值。当外力F≥Ff0时,物体A相对于B发生运动。
2.牛顿定律应用中的一些参考实例
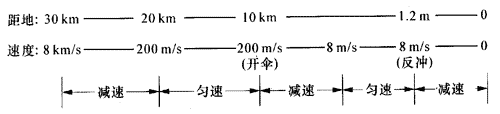
【实例1】神舟号飞船在返回时返回舱以近8km/s的速度进入大气层,当它距离地面30km时,返回舱完成一系列返回准备,当返回舱距地面20km以下的高度后,速度减为200m/s而且匀速下降,此段过程中返回舱所受空气阻力为Ff=
(1)试写出返回舱速度为200m/s时的质量表达式。
(2)分析从打开降落伞到反冲发动机点火前,返回舱的加速度和速度变化情况。
(3)求反冲发动机点火后返回舱受到的阻力为多大?
【分析】本问题文字较长,不妨将其全过程画一个示意图(图3 - 11)。
(1)速度达200m/s后,返回舱做匀速运动,则mg-Ff=0,即mg-
(2)打开降落伞后,合外力方向向上,加速度向上,加速度的大小,先增大后减小,速度不断减小,做减速运动,直到以8m/s做匀速运动时,加速度减小到0。
(3)设反冲发动机点火后,返回舱受到总阻力为F,若最后阶段看作匀变速运动,根据牛顿第二定律F-mg=ma,a=

【实例2】图3 -12是某报纸报道香港新建的一种让人体验落体感觉的“跳楼机”,其中列出了如下一些数据:
(1)极速30s;
(2)总高度60m;
(3)时速45英里(1英里=1609m,此速度相当于20m/s);
(4)乘载12人;
(5)只有1min时间。
请判断一下,哪些数据是明确的?哪些是不太明确的?有没有矛盾之处?整个运动过程究竟是如何进行的?
【分析】该跳楼机的运动过程可能是非匀变速运动。报道时数据采集本身可能有差错,因此只要根据信息作出一个能自圆其说的、与实际相接近的结论就可以了,上述数据中比较明确的是总高度60m,乘载12人。而“极速30s”“速度20m/s,以及“1min时间”均不太明确,下落过程30s显得太长。20m/s若是全程平均速度又太大,因此这里的速度应当是下降过程中的最大速度。开始下降阶段加速度接近重力加速度,达到最大速度之后即做减速运动,抵达地面,根据这一分析可以作出许多具体的估计。
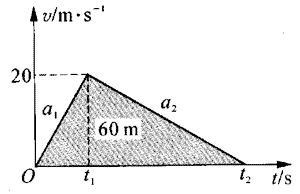
大致画出下降过程的v-t图,如图3- 13所示,t1是“跳楼机”以接近g的加速度下降的时间,设a1≈9.2m/s2,则
t1=vt/a1 =20/9.2 s≈2.2 s。
其减速过程也看作匀减速运动,则全过程总时间为
t2=2s/v =60×2/20 s=6s,即减速时间为3.8s。
由此可算出跳楼机箱体做减速运动时的加速度为a2=-vt/t2 =-20/3.8 m/s=-5.3m/s,从而可估计出做减速运动时钢索对箱体的拉力F(设箱体和人总质量为1t)。
根据牛顿第二定律,F-mg=ma,即F=m(g+a)=103×(10+5.3)N=1.53×105N。
若文中所说“极速时间”30s,指的是牵引上升加下降的总时间,那么将游客匀速向上提升的时问应是30-6=24s,所以上升的速度
v=s/t =60/24 m/s=2.5m/s。
最后要解释的是“1min”指的是什么,那么就应该是指游客从上机到下机的时间也是30s,两段时间相加即1min。这是一道开放性题目,上述提供的是一种解释,还可以作出其他解释。
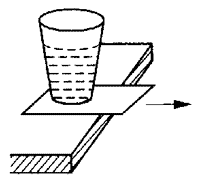
【实例3】如图3 -14所示,玻璃杯底压一张纸,用手将纸以很大的均匀速率抽出,由于作用时间短,玻璃杯只有很小的位移,如果抽纸的速率相同,压纸的位置也相同,而杯中水质量不同,试分析杯子的位移大小与杯中盛水多少的关系。
有的同学根据质量是物体惯性大小的量度,所以得出杯子中水越多,质量越大,惯性也越大,所以运行的值移就会越小。
还有的同学认为生活中的感受告诉我们:质量越大的物体动作越迟缓,运动后不容易停下来,所以杯子中水越多,则位移也越大,究竟哪一种说法对呢?
【分析】其实,上面两种分析方法都是错误的,原因是他们没有采用科学的方法进行分析,一种方法是片面的分析问题,另一种方法是受到生活中的感觉影响,他们的思维都偏离正确的、科学的思维方法,所以得出错误的结论。
要正确得出杯子的位移与杯子总质量的关系,首先要弄清楚杯子为什么发生位移?也就是要找出问题的根源;其次要分析这个位移是怎么发生的?也就是要弄清楚杯子的运动的物理过程;最后运用物理规律进行求解。
杯子之所以发生位移是因为开始时纸对杯子有摩擦力作用使其做匀加速运动,当纸被抽出后,摩擦力的作用使其又做匀减速直线运动,最后停止下来。设杯子与纸之间的动摩擦因数为μ,则由牛顿运动定律得:
μ1mg=ma1,a1=μ1g。
则杯子在匀加速运动中的位移为:
s1=
因为压住纸的位置相同,抽纸的速率也相同,所以所用的时间也相同,因此s1相同,s1与质量m无关。
在杯子做匀减速直线运动的过程中,初速度v0=a1t,加速度a2=μ2g(μ2是玻璃杯与桌面间的动摩擦因数)。
则匀减运动的过程中的位移s2=v02/2a2 =a12t2/2μ2g 。
由此得s2与质量m也无关。
综上所述,杯子的位移大小与质量没有关系,只与动摩擦因数有关,所以位移相同。
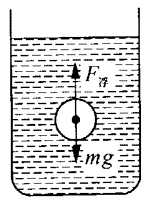
【实例4】如图3 -15所示,一个密度为ρ的木球浸没于密度为ρ0的水中,由于ρ<ρ0,木球将向上加速浮起。木球上浮的加速度多大(不计上浮时受到的阻力)?有人采用的计算方法是:
F浮-mg=ma。
设木球体积为V,则应有
ρ0gV-ρgV=ρVa,
得a=
这样的计算方法是否正确呢?试加以判断。
【分析】对于上面的结论,让我们举几个特殊例子来看一看。
(1)当木球的密度是水的密度的一半时,即ρ=
a=
木球的向上加速度与自由落体的加速度相当。
(2)当木球的密度是水密度的
a=
木球的向上加速度可达到重力加速度的3倍。
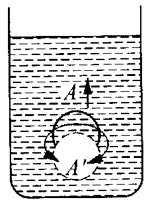
若密度更小的话,加速度将更大,这是可能的吗?这种计算方法明显不符合实际情况,实际上木球上浮的加速度是很难达到g的,我们不妨设想木球变成一个气泡(图3 - 16所示),它上升时实质上是有相同体积的水在下降,即使不计任何阻力,水下降的加速度只能等于g。而按前面的算法,a将趋于无穷大,这当然是不可能的。
实质上木球上升时必定有相同体积的水在下降,它们之间一定有相互作用,不能只简单考虑木球的运动。因此本问题的计算方法是不正确的,至于加速度应当如何计算则比较复杂,此处不再作定量讨论。
文件下载(已下载 181 次)发布时间:2013/12/26 上午8:09:07 阅读次数:2588
