第二章 力矩 有固定转动轴物体的平衡参考资料
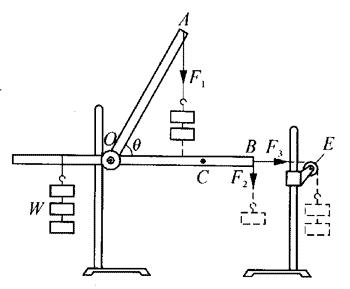
1.演示力臂和力矩的自制三臂杠杆
用木条自制一个有三个共轴于O点的刚性臂的杠杆,如图1所示。为便于讲解,可以令OA=OB,θ=60°。在左臂加配重W,先在A点挂钩码施力F1使杠杆平衡,然后在A点去掉F1,而将F1改施于C点,却不能平衡,改为在B点施力F2才又达到平衡。上述现象表明:F1和F2对物体的转动有相等的效果,这是因为F1和F2产生的力矩是相同的。继续用上述仪器做演示:用力F1或F2施力矩使杠杆平衡后,通过定滑轮E对杠杆施加沿OB方向的力F3,可以看到无论F3多大,对杠杆的平衡都不产生影响,表明F3不产生力矩,进一步完善对力臂的认识。
2.伦敦塔桥
英国伦敦泰晤士河上的桥梁中最为著名的是伦敦塔桥,它的造型独特而雄伟,采用哥特式的建筑风格。塔桥桥身由四座塔楼连接而成,两侧的两座小塔楼建在岸上,两座主塔楼高42.7m,建在桥墩上,塔楼内设有博物馆、展览厅、商店、酒吧等。两座主塔楼之间为双层桥,上层为固定的步行桥,下层为可以开合的活动桥,平常供行人和车辆行走,如有大型海轮通过时,桥面便会缓缓从中间断开,然后向上立起,待船通过后,再缓慢放下桥面,恢复原样。两块活动桥面,各重1000t。伦敦塔桥建于19世纪末期,历时9年,1894年6月30日对公众开放。

3.一般的物体平衡条件
正如本章B节课本第20页的“拓展联想”栏目中所说,一般的物体平衡条件包括“力平衡条件”和“力矩平衡条件”,一个物体若处于(力学)平衡状态,则作用在该物体上的所有外力之和为零;所有外力矩之和为零。这平衡条件可用公式表示为:
\(\sum\limits_i {{F_{ix}} = 0} ,\sum\limits_i {{F_{iy}} = 0} ,\sum\limits_i {{M_i} = 0} \)。
其中Fix,Fiy分别为第i个外力的x分量和y分量,M为第i个力矩,且规定逆时针方向力矩为正,顺时针方向力矩为负。可见,在高中物理基础型教材中介绍的“共点力平衡条件”和本章中讨论的“有固定转动轴的物体的(力矩)平衡条件”是上述一般物体平衡条件的两种特例。
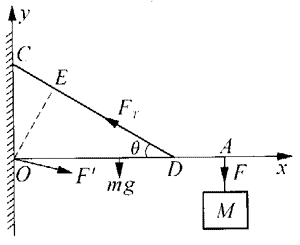
例如,本章B节示例1中只需应用力矩平衡条件,对物OA受力分析时,不必考虑其作用线通过转轴的力,实际上,此时墙壁对横杆OA有作用力,如图3所示,不过这个力的作用点在转轴O上,它的力臂为零,因此力矩为零。利用力平衡条件,可计算该题中作用在O点的力Fʹ。根据该示例的结果,钢丝的拉力FT=170N。它的x方向分量为FTx=-FTcosθ=-147N;y方向分量FTy=FTsinθ=85N。因此Fʹ的x方向分量Fxʹ=-FTx≈147N;y方向分量Fyʹ=-[FTy-mg-Mg]≈-16.4N。
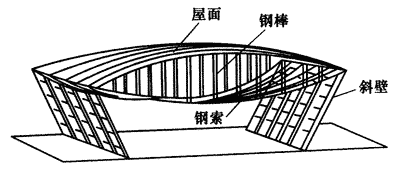
4.一个关于上海浦东国际机场候机楼设计中的力学问题
上海浦东国际机场候机楼的设计与众不同,它的侧壁是倾斜的,用钢索将两边斜壁系住,在钢索上竖有许多短钢棒将屋面支撑在钢索上,甚为壮观(见图4)。

候机楼结构可简化如图5所示。这种设计的优点是,利用两侧斜壁向外倾倒的趋势,将钢索拉紧,而拉紧的钢索能承重,从而将屋面托住。下面,我们做一些假设,请你通过计算了解其设计的巧妙之处。
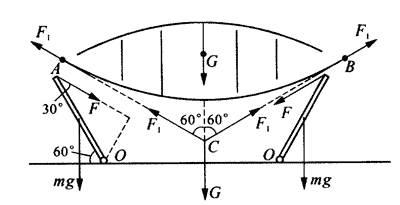
假设一面斜壁质量为m,分布均匀,在地面处有一固定转轴O(图6),斜壁可绕O点转动,此时斜壁与地面夹角为60°,斜壁上端所有钢索的总拉力为F,与斜壁夹角为30°,设屋面通过短钢棒支撑在钢索上。
(1)求所有钢索的总拉力F的大小。
(2)钢索能承担多重的屋面?
【分析】图6已画出了斜壁和屋面的受力图,求钢索的总拉力F,可以用力矩平衡的原理,对AO壁来说,顺时针方向的拉力矩等于逆时针方向的重力矩。对屋面来说可以看作共点力的平衡,设OA与OB的长度为l,两边钢索总拉力F的反作用力F1与屋面的重力G交汇于C点,处于三力平衡状态。
【解答】(1)mg•\(\frac{l}{2}\) •cos60°=F•l•sin30°,
F=\(\frac{{mg}}{2}\)
(2)2Fsin30°=G,
G=F=\(\frac{{mg}}{2}\)
所以钢索总拉力为\(\frac{{mg}}{2}\),能承受屋面重力也为\(\frac{{mg}}{2}\)。
【讨论】实际上斜壁底部不是固定在转轴上,而是固定在坚固地基上的,因此它能承担的屋面重力还可以更大一些。浦东国际机场候机楼的设计巧妙地利用了力和力矩的平衡条件。
文件下载(已下载 188 次)发布时间:2013/12/19 上午7:41:17 阅读次数:2711
