第二讲动能定理参考资料

1．变力做功情况下动能定理的推导

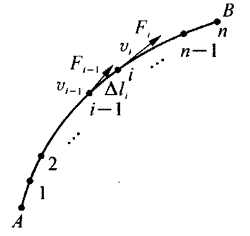
如果物体在变力F作用下沿图1所示的曲线AB运动，我们就可照过去已使用过的办法，把从A到B的运动路径分成n段，每一小段位移Δl_i可以近似认为是在恒力F_i作用下做直线运动，如果物体在起始点A处的速度为v_A，在终点B处的速度为v_B，可有

$\begin{array}{l} W_{1} = \frac{1}{2} m v_{1}^{2} - \frac{1}{2} m v_{A}^{2}, \\ W_{2} = \frac{1}{2} m v_{2}^{2} - \frac{1}{2} m v_{1}^{2}, \\ \dots \\ W_{i} = \frac{1}{2} m v_{i}^{2} - \frac{1}{2} m v_{i - 1}^{2}, \\ \dots \\ W_{n} = \frac{1}{2} m v_{B}^{2} - \frac{1}{2} m v_{n - 1}^{2} . \end{array}$

将所有这些式子相加，并取极限，即令n→∞，则在物体从A到B的整个过程中外力所做的功为

$W = lim_{n \to \infty} \sum_{i = 1}^{n} W_{i} = \frac{1}{2} m v_{B}^{2} - \frac{1}{2} m v_{A}^{2}$ 。

这表明动能定理在这种情况下也是成立的。

2．物体系的动能定理

物体系统，或简称为物体系，就是由两个或两个以上的物体组成的研究对象。当物体系统中的相互作用力是保守力时，物体系统具有势能，系统内各物体之间具有相互作用是它们的基本特点。

如果我们以某一物体系作为研究对象，则该物体系内所有物体之间的各种相互作用力统称为内力，其他物体对系统内物体的作用力称为外力。

当研究对象改变时，同一对物体间的作用力就可能从内力变为外力或从外力变为内力。例如，若以太阳系作为一个物体系来研究，则太阳对地球的引力为内力；若以地球及其上的物体作为一个物体系统来研究，则太阳对地球的引力就是外力。

物体系内各物体的动能之和，称为物体系的动能。设由n个质量分别为m₁、m₂、…、m_n的物体组成的物体系，在某一时刻t₁，各物体的速度分别为v₁₁、v₂₁、…、v_n1，则该物体系此时具有的动能为

$E_{k} = \frac{1}{2} m_{1} v_{11}^{2} + \frac{1}{2} m_{2} v_{21}^{2} + \dots + \frac{1}{2} m_{n} v_{n 1}^{2} = \sum_{i = 1}^{n} \frac{1}{2} m_{i} v_{i 1}^{2}$ 。

当物体系的运动状态发生变化后，根据单一物体的动能定理，对物体系中的第i个物体有

$\frac{1}{2} m_{i} v_{i 2}^{2} - \frac{1}{2} m_{i} v_{i 1}^{2} = W_{i}$ ，

式中v_i2为第i个物体在时刻t₂时的速度，W_i为发生这一状态变化的过程中，第i个物体受到的所有力对它所做的功。这里说的所有力包括两部分，一部分是物体系内其他物体对第i个物体的作用力之和，即所谓内力；另一部分是物体系以外的其他物体对第i个物体的作用力之和，即所谓外力，相应地，功W_i也可以分为内力的功W_i外和外力的功W_i内。于是上式可写为

$\frac{1}{2} m_{i} v_{i 2}^{2} - \frac{1}{2} m_{i} v_{i 1}^{2} = W_{i} 外 + W_{i} 内$ 。

W_i外与W_i内分别代表所有外力对第i个物体做功之和与所有内力对第i个物体做功之和，对物体系内所有的物体均可写出类似关系，求和可得

$(\frac{1}{2} m_{1} v_{12}^{2} + \frac{1}{2} m_{2} v_{22}^{2} + \dots \frac{1}{2} m_{n} v_{n 2}^{2}) - (\frac{1}{2} m_{1} v_{11}^{2} + \frac{1}{2} m_{2} v_{21}^{2} + \dots \frac{1}{2} m_{n} v_{n 1}^{2}) = (W_{i} 外 + W_{i} 外 + \dots W_{n} 外) + (W_{i} 内 + W_{i} 内 + \dots W_{n} 内)$ ，

即

$\sum_{i = 1}^{n} \frac{1}{2} m_{i} v_{i 2}^{2} - \sum_{i = 1}^{n} \frac{1}{2} m_{i} v_{i 1}^{2} = \sum_{i = 1}^{n} W_{i} 外 + \sum_{i = 1}^{n} W_{i} 内$ 。

于是有

E_k2－E_k1＝W_外＋W_内，

式中E_k1和E_k2分别为物体系始、末两态的动能，W_外是所有外力对物体系所有物体做的功的代数和，简称外力的总功，W_内是内力对所有物体做的功的代数和，简称内力的总功。

上式表明，物体系的动能增量等于外力的总功和内力的总功的代数和，这称为物体系的动能定理。所谓动能的增量是指末态的动能减去初态的动能，并非一定意味着动能要增加，增量可以是负值，那就意味着减小，在物理学中，经常使用增量这个词，其含义与动能的增量相同。

（摘编自赵凯华《新概念中学物理读本》）

文件下载（已下载 185 次）

发布时间：2013/12/2 上午11:52:41 阅读次数：1770

第二讲 动能定理参考资料

1．变力做功情况下动能定理的推导

2．物体系的动能定理

评论

第二讲动能定理参考资料