1．电磁波与机械波具有的共同性质是（    ）

（A）都是横波                                     （B）都能传输能量

（C）都能在真空中传播                     （D）都具有恒定的波速

【答案】

B

 

2．当用一束紫外线照射锌板时，产生了光电效应，这时（    ）

（A）锌板带负电                         （B）有正离子从锌板逸出

（C）有电子从锌板逸出             （D）锌板会吸附空气中的正离子

【答案】

C

 

3．白光通过双缝后产生的干涉条纹是彩色的，其原因是不同色光的（    ）

（A）传播速度不同             （B）强度不同

（C）振动方向不同             （D）频率不同

【答案】

D

 

4．做简谐振动的物体，当它每次经过同一位置时，可能不同的物理量是（    ）

（A）位移             （B）速度             （C）加速度         （D）回复力

【答案】

B

 

5．液体与固体具有的相同特点是（    ）

（A）都具有确定的形状                     （B）体积都不易被压缩

（C）物质分子的位置都确定             （D）物质分子都在固定位置附近振动

【答案】

B

 

6．秋千的吊绳有些磨损。在摆动过程中，吊绳最容易断裂的时候是秋千（    ）

（A）在下摆过程中                     （B）在上摆过程中

（C）摆到最高点时                     （D）摆到最低点时

【答案】

D

 

7．在一个 ²³⁸₉₂U 原子核衰变为一个 ²⁰⁶₈₂Pb 原子核的过程中，发生 β 衰变的次数为（    ）

（A）6 次              （B）10 次            （C）22 次            （D）32 次

【答案】

A

 

8．如图，质量 m_A ＞ m_B 的两物体 A、B 叠放在一起，靠着竖直墙面。让它们由静止释放，在沿粗糙墙面下落过程中，物体 B 的受力示意图是 （     ）

【答案】

A

【解析】

A、B 在竖直下落过程中与墙面没有弹力，所以也没有摩擦力，A、B 均做自由落体运动，均只受重力，故 A 正确。

 

9．小行星绕恒星运动，恒星均匀地向四周辐射能量，质量缓慢减小，可认为小行星在绕恒星运动一周的过程中近似做圆周运动。则经过足够长的时间后，小行星运动的（      ）

（A）半径变大             （B）速率变大             （C）角速度变大            （D）加速度变大

【答案】

A

 

10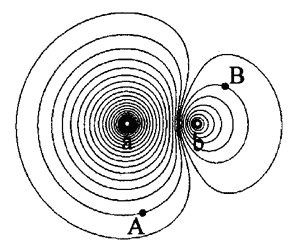．两异种点电荷电场中的部分等势面如图所示，已知 A 点电势高于 B 点电势。若位于 a、b 处点电荷的电荷量大小分别为 q_a 和 q_b，则 （      ）

（A）a 处为正电荷，q_a ＜ q_b

（B）a 处为正电荷，q_a ＞ q_b

（C）a 处为负电荷，q_a ＜ q_b

（D）a 处为负电荷，q_a ＞ q_b

【答案】

B

 

11．如图，通电导线 MN 与单匝矩形线圈 abcd 共面，位置靠近 ab 且相互绝缘。当 MN 中电流突然减小时，线圈所受安培力的合力方向（      ）

（A）向左                             （B）向右

（C）垂直纸面向外             （D）垂直纸面向里

【答案】

B

 

12．在车门报警电路中，两个按钮开关分别装在汽车的两扇门上，只要有开关处于断开状态，报警灯就发光。能实现此功能的电路是（      ）

【答案】

D

 

13．如图，足够长的直线 ab 靠近通电螺线管，与螺线管平行。用磁传感器测量 ab 上各点的磁感应强度 B，在计算机屏幕上显示的大致图像是（      ）

【答案】

C

 

14．一列横波沿水平绳传播，绳的一端在 t ＝ 0 时开始做周期为 T 的简谐运动，经过时间 t（$\frac{3}{4}$T ＜ t ＜ T），绳上某点位于平衡位置上方的最大位移处。则在 2t 时，该点位于平衡位置的 （     ）

（A）上方，且向上运动    （B）上方，且向下运动

（C）下方，且向上运动    （D）下方，且向下运动

【答案】

A

 

15．已知湖水深度为 20 m，湖底水温为 4 ℃，水面温度为 17 ℃，大气压强为 1.0×10⁵ Pa。当一气泡从湖底缓慢升到水面时，其体积约为原来的（取 g ＝ 10 m/s²，ρ_水 ＝ 1.0×10³ kg/m³ ）（      ）

（A）12.8 倍    （B）8.5 倍    （C）3.1 倍    （D）2.1 倍

【答案】

C

 

16．汽车以恒定功率沿公路做直线运动，途中通过一块沙地。汽车在公路及沙地上所受阻力均为恒力，且在沙地上受到的阻力大于在公路上受到的阻力。汽车在驶入沙地前己做匀速直线运动，它在驶入沙地到驶出沙地后的一段时间内，位移 s 随时间 t 的变化关系可能是 （      ）

【答案】

A

 

17．某半导体激光器发射波长为 1.5×10⁻⁶ m，功率为 5.0×10⁻³ W 的连续激光。已知可见光波长的数量级为 10⁻⁷ m，普朗克常量 h ＝ 6.63×10⁻³⁴ J•s，该激光器发出的 （       ）

（A）是紫外线                                     （B）是红外线

（C）光子能量约为 1.3×10⁻¹⁸ J         （D）光子数约为每秒 3.8×10¹⁶ 个

【答案】

BD

 

18．两个共点力 F₁、F₂ 大小不同，它们的合力大小为 F，则 （      ）

（A）F₁、F₂ 同时增大一倍，F 也增大一倍

（B）F₁、F₂ 同时增加 10 N，F 也增加 10 N

（C）F₁ 增加 10 N，F₂ 减少 10 N，F 一定不变

（D）若 F₁、F₂ 中的一个增大，F 不一定增大

【答案】

AD

 

19．如图，轰炸机沿水平方向匀速飞行，到达山坡底端正上方时释放一颗炸弹，并垂直击中山坡上的目标 A。已知 A 点高度为 h，山坡倾角为 θ，由此可算出 （      ）

（A）轰炸机的飞行高度             （B）轰炸机的飞行速度

（C）炸弹的飞行时间                 （D）炸弹投出时的动能

【答案】

ABC

 

20．右图为在平静海面上，两艘拖船 A、B 拖着驳船 C 运动的示意图。A、B 的速度分别沿着缆绳 CA、CB 方向，A、B、C 不在一条直线上。由于缆绳不可伸长，因此 C 的速度在 CA、CB 方向的投影分别与 A、B 的速度相等，由此可知 C 的 （      ）

（A）速度大小可以介于 A、B 的速度大小之间

（B）速度大小一定不小于 A、B 的速度大小

（C）速度方向可能在 CA 和 CB 的夹角范围外

（D）速度方向一定在 CA 和 CB 的夹角范围内

【答案】

BC

 

21．放射性元素 ²¹⁰₈₄Po 衰变为 ²⁰⁶₈₂Pb，此衰变过程的核反应方程是__________；用此衰变过程中发出的射线轰击 ¹⁹₉F，可得到质量数为 22 的氖（Ne）元素和另一种粒子，此核反应过程的方程是 ________。

【答案】

²¹⁰₈₄Po→²⁰⁶₈₂Pb ＋ ⁴₂He，¹⁹₉F ＋ ⁴₂He→²²₁₀Ne ＋ ¹₁H

 

22．质量为 M 的物块静止在光滑水平桌面上，质量为 m 的子弹以水平速度 v₀ 射入物块后，以水平速度 $\frac{2}{3}$v₀ 射出。则物块的速度为________，此过程中损失的机械能为 _______。

【答案】

$\frac{m}{3M}$v₀，$\frac{1}{18}$（5 − $\frac{m}{M}$）mv₀²

 

22．若两颗人造地球卫星的周期之比为 T₁∶T₂ ＝ 2∶1，则它们的轨道半径之比 R₁∶R₂ ＝_______，向心加速度之比 a₁∶a₂ ＝ ________。

【答案】

$\sqrt[3]{4}$∶1，1∶$\sqrt[3]{16}$

 

23．如图，在半径为 2.5 m 的光滑圆环上切下一小段圆弧，放置于竖直平面内，两端点距最低点高度差 H 为 1 cm。将小环置于圆弧端点并从静止释放，小环运动到最低点所需的最短时间为_________s，在最低点处的加速度为________m/s²。（取g ＝ 10 m/s²）

【答案】

$\frac{\pi }{4}$ ≈ 0.785，0.08

 

24．如图，电路中三个电阻 R₁、R₂ 和 R₃ 的阻值分别为 R、2R 和 4R。当电键 S₁ 断开、S₂ 闭合时，电源输出功率为 P₀；当 S₁ 闭合、S₂ 断开时，电源输出功率也为 P₀。则电源电动势为______；当 S₁、S₂ 都断开时，电源的总功率为 _______。

【答案】

3$\sqrt{P_{0}R}$，P₀

【解析】

（1）当电键 S₁ 断开、S₂ 闭合时，R₂、R₃ 被短路，外电路只有 R₁ 一个电阻，有：

P₀ = ($\frac{E}{R_1+r}$)²R₁ = ($\frac{E}{R+r}$)²R

当电键 S₁ 闭合、S₂ 断开时，R₁、R₂ 被短路，外电路只有 R₃ 一个电阻，有：

P₀ = ($\frac{E}{R_3+r}$)²R₃ = ($\frac{E}{4R+r}$)²4R

联立以上两式，可求得 E = 3$\sqrt{P_{0}R}$，r = 2R

（2）当 S₁、S₂ 都断开时，外电阻为 R₁、R₂、R₃ 三者串联，有：

P_总 = $\frac{E^2}{R_1+R_2+R_3+r}$ = $\frac{{(3\sqrt{P{R}_0})}^2}{9R}$ = P₀

 

25．如图，倾角为 37°，质量不计的支架 ABCD 的 D 端有一大小与质量均可忽略的光滑定滑轮，A 点处有一固定转轴，CA⊥AB，DC ＝ CA ＝0.3 m。质量 m ＝ 1 kg 的物体置于支架的B端，并与跨过定滑轮的轻绳相连，绳另一端作用一竖直向下的拉力 F，物体在拉力作用下沿 BD 做匀速直线运动，己知物体与 BD 间的动摩擦因数 μ ＝ 0.3。为保证支架不绕 A 点转动，物体向上滑行的最大距离 s ＝________m。若增大 F 后，支架仍不绕A点转动，物体能向上滑行的最大距离 sʹ________s（填：“大于”、“等于”或“小于”。）（取 sin37° ＝ 0.6，cos37° ＝ 0.8 ）

【答案】

0.248，等于

【解析】

以 m 为研究对象，N = mgcos37° = 8 N，f = μN = 2.4 N，F = mgsin37° + f = 8.4 N。以支架为研究对象，以 A 为支点，由几何关系知力 F 的力臂为 l₁ = 0.24 m，摩擦力和平行斜面细线拉力的力臂为 l₂ = 0.24 m，压力的力臂为 l₃ = 0.32 m − s，由力矩平衡得 Fl₁ + fl₂ = Nl₃ + Fl₂，解得 s = 0.248 m。由于 l₁ = l₂，可见增大 F 后，物体向上滑行的最大距离不变，即 sʹ = s。

 

26．演示地磁场存在的实验装置（由环形线圈，微电流传感器，DIS 等组成）如图所示。首先将线圈竖直放置，以竖直方向为轴转动，屏幕上的电流指针________（填：“有”或“无”）偏转；然后仍将线圈竖直放置，使其平面与东西向平行，并从东向西移动，电流指针_______（填：“有”或“无”）偏转；最后将线圈水平放置，使其从东向西移动，电流指针________（填：“有”或“无”）偏转 。

【答案】

有，无，无

 

27．为确定某电子元件的电气特性，做如下测量。

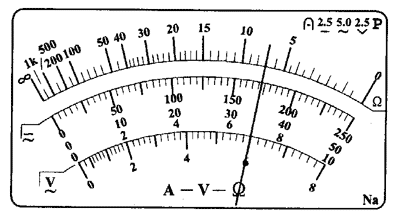
（1）用多用表测量该元件的电阻，选用“×100”倍率的电阻档测量，发现多用表指针偏转过大，因此需选择________倍率的电阻档（填：“×10”或“×1 k”），并_______再进行测量，多用表的示数如图（a）所示，测量结果为_______Ω 。

（2）将待测元件（额定电压 9 V）、蓄电池、滑动变阻器、电流表、多用表、电键及若干导线连接成电路如图（b）所示。添加连线，使电路能测量该元件完整的伏安特性。本实验中使用多用表测电压，多用表的选择开关应调到_______档（填：“直流电压 10 V”或“直流电压 50 V”）。

【答案】

（1）×10，重新调零，70

（2）连线如图，直流电压 10 V

 

28．如图，研究平抛运动规律的实验装置放置在水平桌面上，利用光电门传感器和碰撞传感器可测得小球的水平初速度和飞行时间，底板上的标尺可以测得水平位移。保持水平槽口距底板高度 h ＝ 0.420 m 不变。改变小球在斜槽导轨上下滑的起始位置，测出小球做平抛运动的初速度 v₀、飞行时间 t 和水平位移 d，记录在表中 。

v0（m/s）	0.741	1.034	1.318	1.584
t（ms）	292.7	293.0	292.8	292.9
d（cm）	21.7	30.3	38.6	46.4

（1）由表中数据可知，在 h 一定时，小球水平位移 d 与其初速度 v₀ 成______关系，与______无关。

（2）一位同学计算出小球飞行时间的理论值 t_理 ＝ $\sqrt{\frac{2h}{g}}$ ＝ $\sqrt{\frac{2\times 0.420}{10}}$  ＝ 289.8 ms，发现理论值与测量值之差约为 3 ms。经检查，实验及测量无误，其原因是_________。

（3）另一位同学分析并纠正了上述偏差后，另做了这个实验，竟发现测量值 tʹ 依然大于自己得到的理论值 t_理ʹ，但二者之差在 3 ~ 7 ms 之间，且初速度越大差值越小。对实验装置的安装进行检查，确认斜槽槽口与底座均水平，则导致偏差的原因是_________。

【答案】

（1）正比，飞行时间 t

（2）重力加速度值取值不正确

（3）光电门传感器置于槽口的内侧（或小球直径过大、小球飞过光电门需要时间）

 

29． 利用如图装置可测量大气压强和容器的容积。步骤如下：

①将倒 U 形玻璃管 A 的一端通过橡胶软管与直玻璃管 B 连接，并注入适量的水，另一端插入橡皮塞，然后塞住烧瓶口，并在 A 上标注此时水面的位置 K；再将一活塞置于 10 ml 位置的针筒插入烧瓶，使活塞缓慢推移至 0 刻度位置；上下移动 B，保持 A 中的水面位于 K 处，测得此时水面的高度差为 17.1 cm。

②拔出橡皮塞，将针筒活塞置于 0 ml 位置，使烧瓶与大气相通后再次塞住瓶口；然后将活塞抽拔至 10 ml 位置，上下移动 B，使 A 中的水面仍位于 K，测得此时玻璃管中水面的高度差为 16.8 cm。（玻璃管A内气体体积忽略不计，ρ_水 ＝ 1.0×10³ kg/m³，取 g ＝ 10 m/s²）

（1）若用 V₀ 表示烧瓶容积，p₀ 表示大气压强，ΔV 表示针筒内气体的体积，Δp₁、Δp₂ 表示上述步骤①、②中烧瓶内外气体压强差大小，则步骤①、②中，气体满足的方程分别为_________、________________。

（2）由实验数据得烧瓶容积 V₀＝_______ml，大气压强 p₀＝_____Pa。

（3）（单选题）倒U形玻璃管 A 内气体的存在 （    ）

（A）仅对容积的测量结果有影响

（B）仅对压强的测量结果有影响

（C）对二者的测量结果均有影响

（D）对二者的测量结果均无影响

【答案】

（1）p₀（V₀ + ΔV）=（p₀ + Δp₁）V₀

p₀V₀ =（p₀ − Δp₂）（V₀ + ΔV）

（2）560，9.58×10⁴

（3）A

 

30．如图，柱形容器内用不漏气的轻质绝热活塞封闭一定量的理想气体，容器外包裹保温材料。开始时活塞至容器底部的高度为 H₁，容器内气体温度与外界温度相等。在活塞上逐步加上多个砝码后，活塞下降到距容器底部 H₂ 处，气体温度升高了 ΔT；然后取走容器外的保温材料，活塞位置继续下降，最后静止于距容器底部 H₃ 处：已知大气压强为 p₀。求：气体最后的压强与温度 。

【答案】

p₃ ＝ $\frac{H_1}{H_3}$p₀

T₃ ＝ $\frac{H_3}{H_2-H_3}$ΔT

【解析】

解：初末状态温度相等，由

p₀H₁S＝p₃H₃S

得p₃＝$\frac{H_1}{H_3}$p₀

活塞位于H₂时，温度T₂＝T₁＋ΔT，然后等压压缩至H₃，且T₃＝T₁，由

$\frac{H_{2}S}{T_2}$＝$\frac{H_{3}S}{T_3}$

得T₃H₂＝（T₃＋ΔT）H₃

解得T₃＝$\frac{H_3}{H_2-H_3}$ΔT

 

31．如图，质量为 M、长为 L、高为 h 的矩形滑块置于水平地面上，滑块与地面间动摩擦因数为 μ；滑块上表面光滑，其右端放置一个质量为 m 的小球。用水平外力击打滑块左端，使其在极短时间内获得向右的速度 v₀，经过一段时间后小球落地。求小球落地时距滑块左端的水平距离。

【答案】

若 $\sqrt{\frac{2h}{g}}$ ＜ $\frac{1}{\mu g}\sqrt{v_0^2-2\mu (1+\frac{m}{M})gL}$，s ＝ vt − $\frac{1}{2}$aʹt² ＝ $\sqrt{\frac{2h}{g}[v_0^2-2\mu (1+\frac{m}{M})gL]}-\mu h$

若 $\sqrt{\frac{2h}{g}}$ ＞ $\frac{1}{\mu g}\sqrt{v_0^2-2\mu (1+\frac{m}{M})gL}$，sʹ ＝ $\frac{v_0^2}{2\mu g}-(1+\frac{m}{M})L$

【解析】

解：小球在滑块上运动时滑块运动满足μ（M＋m）g＝Ma，因此

a＝μ（1＋$\frac{m}{M}$）g

由v²＝v₀²－2aL得小球脱离滑块时滑块的速度

v＝$\sqrt{v_0^2-2\mu (1+\frac{m}{M})gL}$

小球脱离滑块后做自由落体运动，t＝$\sqrt{\frac{2h}{g}}$

小球脱离滑块后滑块加速度aʹ＝μg

滑块的运动时间tʹ＝$\frac{v}{\mu g}$＝$\frac{1}{\mu g}\sqrt{v_0^2-2\mu (1+\frac{m}{M})gL}$

若t＜tʹ，小球落地时滑块尚未停止运动，在时间t内滑块运动距离即小球落地时距滑块左侧的距离

s＝vt－$\frac{1}{2}$aʹt²＝$\sqrt{\frac{2h}{g}[v_0^2-2\mu (1+\frac{m}{M})gL]}-\mu h$

若t＞tʹ，小球落地前滑块已停止运动，则由0＝v²－2aʹsʹ得

v₀²－2μ（1＋$\frac{m}{M}$）gL＝2μgsʹ

sʹ＝$\frac{v_0^2}{2\mu g}-(1+\frac{m}{M})L$

 

32．半径为 R，均匀带正电荷的球体在空间产生球对称的电场；场强大小沿半径分布如图所示，图中 E₀ 已知，E–r 曲线下 O–R 部分的面积等于 R–2R 部分的面积 。

（1）写出 E–r 曲线下面积的单位；

（2）己知带电球在 r ≥ R 处的场强 E ＝ $\frac{kQ}{r^2}$，式中 k 为静电力常量，该均匀带电球所带的电荷量 Q 为多大？

（3）求球心与球表面间的电势差 ΔU；

（4）质量为 m，电荷量为 q 的负电荷在球面处需具有多大的速度可以刚好运动到 2R 处？

【答案】

（1）V（N•m/C）。

（2）Q ＝ $\frac{E_0{R}^2}{k}$

（3）ΔU ＝ $\frac{1}{2}$E₀R

（4）v ＝ $\sqrt{\frac{q{E}_{0}R}{m}}$

【解析】

（1）曲线下面积的单位为V（N•m/C）。

（2）均匀带电球表面处场强E₀＝$\frac{kQ}{R^2}$

∴Q＝$\frac{E_0{R}^2}{k}$

（3）球心与表面间电势差为将单位正电荷由球心移动到球表面过程中电场力的功，其大小即图中三角形面积，因此

ΔU＝$\frac{1}{2}$E₀R

（4）由动能定理有－qΔUʹ＝0－$\frac{1}{2}$mv²

由题意ΔUʹ＝$\frac{1}{2}$E₀R

得v＝$\sqrt{\frac{q{E}_{0}R}{m}}$

 

33．如图，两根相距 l ＝ 0.4 m、电阻不计的平行光滑金属导轨水平放置，一端与阻值 R ＝ 0.15 Ω 的电阻相连。导轨 x ＞ 0 一侧存在沿 x 方向均匀增大的稳恒磁场，其方向与导轨平面垂直，变化率 k ＝ 0.5 T/m，x ＝ 0 处磁场的磁感应强度 B₀ ＝ 0.5 T。一根质量 m ＝ 0.1 kg、电阻 r ＝ 0.05 Ω 的金属棒置于导轨上，并与导轨垂直。棒在外力作用下从 x ＝ 0 处以初速度 v₀ ＝ 2 m/s 沿导轨向右运动，运动过程中电阻上消耗的功率不变。求 ：

（1）回路中的电流；

（2）金属棒在 x ＝ 2 m 处的速度；

（3）金属棒从 x ＝ 0 运动到 x ＝ 2 m 过程中安培力做功的大小；

（4）金属棒从 x ＝ 0 运动到 x ＝ 2 m 过程中外力的平均功率。

【答案】

（1）I ＝ 2 A

（2）v = $\frac{2}{3}$m/s

（3）W_Fm ＝ 1.6 J

（4）$\overline{P}$  = 0.7 W

【解析】

解：（1）电阻上消耗的功率恒定即电流恒定

∴I＝$\frac{B_{0}l{v}_0}{R+r}$＝$\frac{0.5\times 0.4\times 2}{0.2}$A＝2A

（2）由题意，磁感应强度B＝B₀＋kx

考虑到电流恒定，有

$\frac{B{}_{0}l{v}_0}{R+r}=\frac{(B_0+kx)lv}{R+r}$

解得$v=\frac{B_0{v}_0}{B_0+kx}=\frac{0.5\times 2}{0.5+0.5\times 2}m/s=\frac{2}{3}m/s$

（3）棒受到的安培力 F_m＝BIl＝（B₀＋kx）Il＝0.4（1＋x）

安培力随位置线性变化

∴$W_{F_m}=\frac{1}{2}[B_0+B_0+kx]Ilx$

代入数值后得W_Fm＝1.6J

（4）由动能定理$W_F-W_{F_m}=\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2$，其中外力做功

$W_F=W_{F_m}+\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2=(1.6-\frac{16}{90})J=1.4J$

安培力做功即电阻上消耗的能量，即

$W_{F_m}=I^2(R+r)t$

运动时间

$t=\frac{W_{F_m}}{I^2(R+r)}=\frac{1.6}{2^2\times 0.2}s=2s$

还可以使用以下方法求出运动时间：

磁感应强度随位置线性变化

$q=\frac{\mathrm{\Delta }\mathrm{\Phi }}{R+r}=\frac{(B_0+B_0+kx)lx}{2(R+r)}=\frac{(0.5+0.5+0.5\times 2)\times 0.4\times 2}{2\times 0.2}C=4C$

$t=\frac{q}{I}=\frac{4}{2}s=2s$

∴$\overline{P}=\frac{W_F}{t}=\frac{1.4}{2}W=0.7W$