1．有一放在空气中的玻璃棒，折射率n＝1.5，中心轴线长L＝45cm，一端是半径为R₁＝10cm的凸球面。

1．要使玻璃棒的作用相当于一架理想的天文望远镜（使主光轴上无限远处物成像于主光轴上无限远处的望远系统），取中心轴线为主光轴，玻璃棒另一端应磨成什么样的球面？

2．对于这个玻璃棒，由无限远物点射来的平行入射光束与玻璃棒的主光轴成小角度ϕ₁时，从棒射出的平行光束与主光轴成小角度，求ϕ₂/ϕ₁（此比值等于此玻璃棒望远系统的视角放大率）。

【答案】

第18届全国复赛1

 

2．正确使用压力锅的方法是：将己盖好密封锅盖的压力锅（如图1）加热，当锅内水沸腾时再加盖压力阀S，此时可以认为锅内只有水的饱和蒸气，空气己全部排除。然后继续加热，直到压力阀被锅内的水蒸气顶起时，锅内即已达到预期温度（即设计时希望达到的温度），现有一压力锅，在海平面处加热能达到的预期温度为120℃。某人在海拔5000m的高山上使用此压力锅，锅内有足量的水。

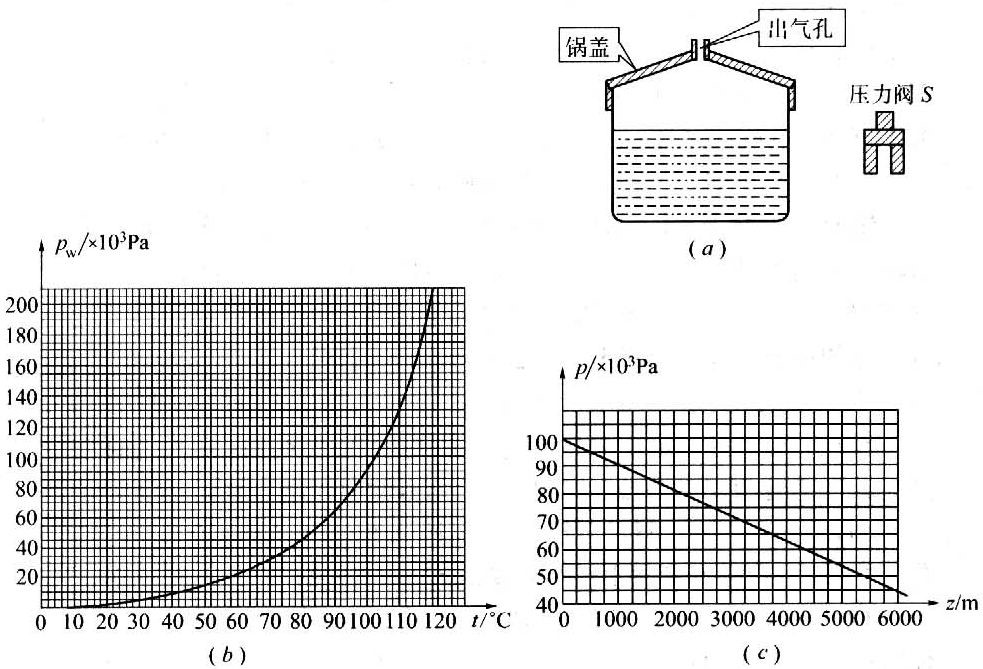
（1）若不加盖压力阀，锅内水的温度最高可达多少？

（2）若按正确方法使用压力锅，锅内水的温度最高可达多少？

（3）若未按正确方法使用压力锅，即盖好密封锅盖一段时间后，在点火前就加上压力阀。此时水温为27℃，那么加热到压力阀刚被顶起时，锅内水的温度是多少？若继续加热，锅内水的温度最高可达多少？假设空气不溶于水。

已知：水的饱和蒸气压p_W(t)与温度t的关系图线如图2所示。

大气压强p(z)与高度z的关系的简化图线如图3所示。

t＝27℃时，p_W（27℃）＝3.6×10³Pa；z＝0处，p（0）＝1.013×10⁵Pa

【答案】

（1）82℃

（2）112℃

（3）97℃，112℃

【解析】

无

 

3．有两个处于基态的氢原子A、B，A静止，B以速度v₀与之发生碰撞。己知：碰撞后二者的速度v_A和v_B在一条直线上，碰撞过程中部分动能有可能被某一氢原子吸收。从而该原子由基态跃迁到激发态，然后，此原子向低能级态跃迁，并发出光子。如欲碰后发出一个光子，试论证：速度v₀至少需要多大（以m/s表示）？己知电子电量为e＝1.602×10^-19C，质子质量为m_p＝1.673×10^-27kg。电子质量为m_e＝0.911×10^-31kg。氢原子的基态能量为E₁＝－13.58eV。

【答案】

第18届全国复赛3

 

4．如图所示，均匀磁场的方向垂直纸面向里，磁感应强度B随时间t变化，B＝B₀－kt（k为大于0的常数）。现有两个完全相同的均匀金属圆环相互交叠并固定在图中所示位置，环面处于图中纸面内。圆环的半径为R，电阻为r，相交点的电接触良好。两个环的接触点A与C间的劣弧对圆心O的张角为60°。求t＝t₀时，每个环所受的均匀磁场的作用力，不考虑感应电流之间的作用。

【答案】

第18届全国复赛4

 

5．如图所示，一薄壁导体球壳（以下简称为球壳）的球心在O点。球壳通过一细导线与端电压U＝90V的电池的正极相连，电池负极接地。在球壳外A点有一电量为q₁＝10×0^-9C的点电荷，B点有一电量为q₂＝16×10^-9C的点电荷。OA之间的距离d₁＝20cm，OB之间的距离d₂＝40cm。现设想球壳的半径从a＝10cm开始缓慢地增大到50cm，问：在此过程中的不同阶段，大地流向球壳的电量各是多少？己知静电力恒量k＝9×10⁹N·m²·C^-2。假设点电荷能穿过球壳壁进入导体球壳内而不与导体壁接触。

【答案】

第18届全国复赛5

 

6．一玩具“火箭”由上下两部分和一短而硬（即劲度系数很大）的轻质弹簧构成。上部分G₁的质量为m₁，下部分G₂的质量为m₂，弹簧夹在G₁与G₂之间，与二者接触而不固连。让G₁、G₂压紧弹簧，并将它们锁定，此时弹簧的弹性势能为己知的定值E₀。通过遥控可解除锁定，让弹簧恢复至原长并释放其弹性势能，设这—释放过程的时间极短。第一种方案是让玩具位于一枯井的井口处并处于静止状态时解除锁定，从而使上部分G₁升空。第二种方案是让玩具在井口处从静止开始自由下落，撞击井底（井足够深）后以原速率反弹，反弹后当玩具垂直向上运动到离井口深度为某值h的时刻解除锁定。

1．在第一种方案中，玩具的上部分G₁升空到达的最大高度（从井口算起）为多少？其能量是从何种形式的能量转化来的？

2．在第二种方案中，玩具的上部分G₁升空可能达到的最大高度（亦从井口算起）为多少？并定量地讨论其能量可能是从何种形式的能量转化来的。

【答案】

第18届全国复赛6