1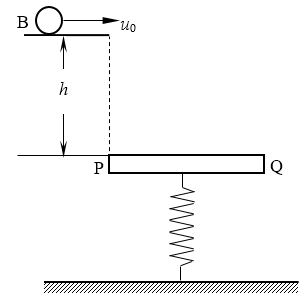．如图所示，一块长为L＝1.00m的光滑平板PQ固定在轻质弹簧上端，弹簧的下端与地面固定连接。平板被限制在两条竖直光滑的平行导轨之间（图中未画出竖直导轨），从而只能地竖直方向运动。平板与弹簧构成的振动系统的振动周期T＝2.00s。一小球B放在光滑的水平台面上，台面的右侧边缘正好在平板P端的正上方，到P端的距离为h＝9.80m。平板静止在其平衡位置。水球B与平板PQ的质量相等。现给小球一水平向右的速度u₀，使它从水平台面抛出。已知小球B与平板发生弹性碰撞，碰撞时间极短，且碰撞过程中重力可以忽略不计。要使小球与平板PQ发生一次碰撞而且只发生一次碰撞，u₀的值应在什么范围内？取g＝9.8m/s²。

【答案】

0.46m/s＜u₀＜0.71m/s

 

2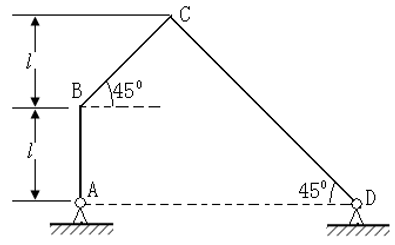．图中所示为用三角形刚性细杆AB、BC、CD连成的平面连杆结构图。AB和CD杆可分别绕过A、D的垂直于纸面的固定轴转动，A、D两点位于同一水平线上。BC杆的两端分别与AB杆和CD杆相连，可绕连接处转动（类似铰链）。当AB杆绕A轴以恒定的角速度ω转到图中所示的位置时，AB杆处于竖直位置。BC杆与CD杆都与水平方向成45°角，已知AB杆的长度为l，BC杆和CD杆的长度由图给定。求此时C点加速度a_C的大小和方向（用与CD杆之间的夹角表示）

【答案】

a_C＝\(\frac{{\sqrt {74} }}{8}\)lω²

故a_C与CD的夹角γ＝80.54°

 

3．如图所示，一容器左侧装有活门K₁，右侧装有活塞B，一厚度可以忽略的隔板M将容器隔成a、b两室，M上装有活门K₂。容器、隔板、活塞及活门都是绝热的。隔板和活塞可用销钉固定，拔掉销钉即可在容器内左右平移，移动时不受摩擦作用且不漏气。整个容器置于压强为p₀、温度为T₀的大气中。初始时将活塞B用销钉固定在图示的位置，隔板M固定在容器PQ处，使a、b两室体积都等于V₀；K₁、K₂关闭。此时，b室真空，a室装有一定量的空气（容器内外气体种类相同，且均可视为理想气体），其压强为\(\frac{4}{5}\)p₀，温度为T₀。已知1mol空气温度升高1K时内能的增量为C_V，普适气体常量为R。

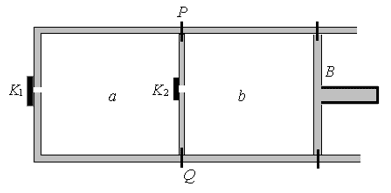
（1）现在打开K₁，待容器内外压强相等时迅速关闭K₁（假定此过程中处在容器内的气体与处在容器外的气体之间无热量交换），求达到平衡时，a室中气体的温度。

（2）接着打开K₂，待a、b两室中气体达到平衡后，关闭K₂。拔掉所有销钉，缓慢推动活塞B直至到过容器的PQ位置。求在推动活塞过程中，隔板对a室气体所作的功。已知在推动活塞过程中，气体的压强p与体积V之间的关系为\(p{V^{\frac{{{C_V} + R}}{{{C_V}}}}}\)＝恒量。

【答案】

（1）T＝\(\frac{{5({C_V} + R)}}{{5{C_V} + 4R}}\)T₀

（2）W＝\(\frac{{{C_V}}}{{2R}}\)（\({2^{\frac{R}{{{C_V}}}}}\)－1）p₀V₀

 

4．图中Oxy是位于水平光滑桌面上的直角坐标系，在x＞0的一侧，存在匀强磁场，磁场方向垂直于Oxy平面向里，磁感应强度的大小为B。在x＜0的一侧，一边长分别为l₁和l₂的刚性矩形超导线框位于桌面上，框内无电流，框的一对边与x轴平行。线框的质量为m，自感为L。现让超导线框沿x轴方向以初速度v₀进入磁场区域，试定量地讨论线框以后可能发生的运动情况及与初速度v₀大小的关系。（假定线框在运动过程中始终保持超导状态）

【答案】

略

 

5．地球赤道表面附近处的重力加速度为g₀＝9.8m/s²，磁场的磁感应强度的大小B₀＝3.0×10^-5T，方向沿经线向北。赤道上空的磁感应强度的大小与r³成反比（r为考察点到地心的距离），方向与赤道附近的磁场方向平行。假设在赤道上空离地心的距离r＝5R_e（R_e为地球半径）处，存在厚度为10km的由等数量的质子和电子的等离子层（层内磁场可视为匀强磁场），每种粒子的数密度非常低，带电粒子的相互作用可以忽略不计。已知电子的质量m_e＝9.1×10^-31kg，质子的质量m_p＝1.7×10^-27kg，电子电荷量为－1.6×10^-19C，地球的半径R_e＝6.4×10⁶m。

（1）所考察的等离子层中的电子和质子一方面作无规则运动，另一方面因受地球引力和磁场的共同作用会形成位于赤道平面内的绕地心的环行电流，试求此环行电流的电流密度。

（2）现设想等离子层中所有电子和质子，它们初速度的方向都指向地心，电子初速度的大小u_e＝1.4×10⁴m/s，质子初速度的大小u_p＝3.4×10²m/s。试通过计算说明这些电子和质子都不可能到到达地球表面。

【答案】

（1）j＝2.8×10^-14A/m²

电流密度的方向沿纬度向东.

（2）计算表明，虽然粒子具有沿引力方向的初速度，但由于粒子还受到磁场的作用，电子和质子在地球半径方向的最大下降距离分别为2R_e＝0.66m和2R_p＝29.6m，都远小于电离层的厚度，所考察的电子和质子仍在等离子层内运动，不会落到地面上。

 

6．图1所示为杨氏双缝干涉实验的示意图，取纸面为yz平面。y、z轴的方向如图所示。线光源S通过z轴，双缝S₁、S₂对称分布在z轴两侧，它们以及屏P都垂直于纸面。双缝间的距离为d，光源S到双缝的距离为l，双缝到屏的距离为D，d≪D，d≪l。

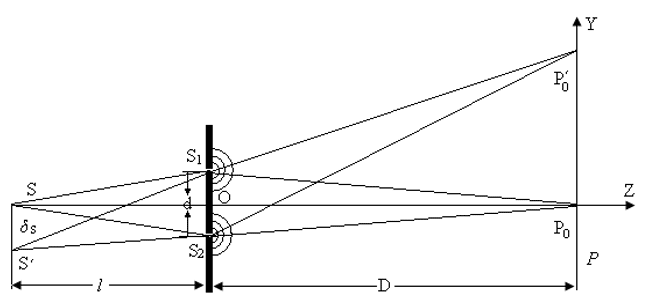
图1

（1）从z轴上的线光源S出发经S₁、S₂不同路径到P₀点的光程差为零，相干的结果产生一亮纹，称为零级亮纹。为了研究有一定宽度的扩展光源对于干涉条纹清晰度的影响，我们先研究位于轴外的线光源S′形成的另一套干涉条纹，S′位于垂直于z轴的方向上且与S平行，两者相距δ_S，则由线光源S′出发分别经S₁、S₂产生的零级亮纹P₀ʹ，P₀ʹ与P₀的距离δ_y＝________________。

（2）当光源宽度为ω的扩展光源时，可将扩展光源看作由一系列连续的、彼此独立的、非相干的线光源组成。这样，各线光源对应的干涉条纹将彼此错开，在屏上看到的将是这些干涉条纹的光强相加的结果，干涉条纹图像将趋于模糊，条纹的清晰度下降。假设扩展光源各处发出的光强相同、波长皆为λ。当ω增大导致零级亮纹的亮暗将完全不可分辨，则此时光源的宽度ω＝______________________。

（3）在天文观测中，可用上述干涉原理来测量星体的微小角直径。遥远星体上每一点发出的光到达地球处都可视为平行光，从星体相对的两边缘点发来的两组平行光之间的夹角θ就是星体的角直径。遥远星体的角直径很小，为测量如些微小的角直径，迈克尔逊设计了测量干涉仪，其装置简化为图2所示。M₁、M₂、M₃、M₄是四个平面反射镜，它们两两平行，对称放置，与入射光（a、a′）方向成45°角。S₁和S₂是一对小孔，它们之间的距离是d。M₁和M₂可以同步对称调节来改变其中心间的距离h。双孔屏到观察屏之间的距离是D。a、a′和b、b′分别是从星体上相对着的两边缘点发来的平行光束。设光线a、a′垂直双孔屏和像屏，星光的波长是\({\bar \lambda }\)，试导出星体上角直径θ的计算式。

注：将星体作圆形扩展光源处理时，研究扩展光源的线度对于干涉条纹图像清晰度的影响会遇到数学困难，为简化讨论，本题拟将扩展光源作宽度为ω的矩形光源处理。

【答案】

（1）\(\frac{D}{l}\)δ_S

（2）\(\frac{l}{d}\)λ

（3）θ＝\(\frac{{\bar \lambda }}{h}\)

 

7．今年是我国著名物理学家、曾任浙江大学物理系主任的王淦昌先生诞生一百周年。王先生早在1941年就发表论文，提出了一种探测中微子的方案：⁷Be原子核可以俘获原子的K层电子而成为⁷Li的激发态（⁷Li）*，并放出中微子（当时写作η）

⁷Be＋e→（⁷Li）*＋η

而（⁷Li）*又可以放出光子γ而回到基态⁷Li

（⁷Li）*→⁷Li＋γ

由于中微子本身很难直接观测，能过对上述过程相关物理量的测量，就可以确定中微子的存在，1942年起，美国物理学家艾伦（R.Davis）等人根据王淦昌方案先后进行了实验，初步证实了中微子的存在。1953年美国人莱因斯（F.Reines）在实验中首次发现了中微子，莱因斯与发现轻子的美国物理学家佩尔（M.L.Perl）分享了1995年诺贝尔物理学奖。

现用王淦昌的方案来估算中微子的质量和动量。若实验中测得锂核（⁷Li）反冲能量（即⁷Li的动能）的最大值E_R＝56.6eV，γ光子的能量hν＝0.48MeV。已知有关原子核和电子静止能量的数据为m_Lic²＝6533.84MeV；m_Bec²＝6534.19MeV；m_ec²＝0.51MeV。设在第一个过程中，⁷Be核是静止的，K层电子的动能也可忽略不计。试由以上数据，算出的中微子的动量p_η和静止质量m_η各为多少？

【答案】

（1）p_η＝0.38MeV/c

（2）所算出的中微子静止质量的数值在题给数据的误差范围之内，故不能确定中微子的静止质量。如果有，其质量一定小于0.1MeV/c²。