1．a、原子大小的数量级为_____________m。

b、原子核大小的数量级为_____________m。

c、氦原子的质量约为_____________kg。

d、一个可见光光子的能量的数量级为_____________J。

e、在标准状态下，1cm³气体中的分子数约为_____________。

（普朗克常量h＝6.63×10^-34J·s，阿伏伽德罗常量N_A＝6.02×10²³mol^-1）

【答案】

a、10^-10，b、10^-15，c、6.6´10^-27，d、10^-19，e、2.7×10¹⁹

 

1．已知某个平面镜反射的光能量为入射光能量的80%，试判断下列说法是否正确，并简述理由。

a、反射光子数为入射光子数的80%；

b、每个反射光子的能量是入射光子能量的80%。

【答案】

a正确，b不正确。理由：反射时光的频率不变，这表明每个光子能量不变。

 

2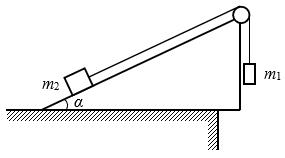．质量分别为m₁和m₂的两个小物块用轻绳连结，绳跨过位于倾角α＝30°的光滑斜面顶端的轻滑轮，滑轮与转轴间的摩擦不计，斜面固定在水平桌面上，如图所示，第一次，m₁悬空，m₂放在斜面上，用t表示m₂自斜面底端由静止开始运动至斜面顶端所需时间，第二次，将m₁和m₂位置互换，使m₂悬空，m₁放在斜面上，发现m₁自斜面底端由静止开始运动至斜面顶端所需的时间为\(\frac{t}{3}\)，求m₁与m₂之比。

【答案】

m₁∶m₂＝11∶19

【解析】

无

 

3．测定电子荷质比（电荷q与质量m之比q/m）的实验装置如图所示，真空玻璃管内，阴极K发出的电子，经阳极A与阴极K之间的高电压加速后，形成一束很细的电子流，电子流以平行于平板电容器极板的速度进入两极板C、D间的区域。若两极板C、D间无电压，则离开极板区域的电子将打在荧光屏上的O点；若在两极板间加上电压U，则离开极板区域的电子将打在荧光屏上的P点；若再在极板间加一方向垂直于纸面向外、磁感应强度为B的匀强磁场，则打到荧光屏上的电子产生的光点又回到O点。现已知极板的长度l＝5.00cm，C、D间的距离d＝1.50cm，极板区的中点M到荧光屏中点O的距离为L＝12.50cm，U＝200V，P点到O点的距离y＝OP＝3.0cm，B＝6.3×10^-4T，试求电子的荷质比。（不计重力影响）

【答案】

1.6×10¹¹C/kg

 

4．要使一颗人造地球卫星（同步卫星）能覆盖赤道上东经75.0°到东经135.0°之间的区域，则卫星应定点在哪个经度范围内的上空？地球半径R₀＝6.37×10⁶m。地球表面重力加速度g＝9.80m/s²。

【答案】

范围是53.7°到156.3°之间的上空

 

5．如图所示，两条平行的长直金属细导轨KL、PQ固定于同一水平面内，它们之间的距离为l，电阻可忽略不计，ab和cd是两根质量皆为m的金属细杆，杆与导轨垂直，且与导轨良好接触，并可沿导轨无摩擦地滑动，两杆的电阻皆为R，杆cd的中点系一轻绳，绳的另一端绕过轻的定滑轮悬挂一质量为M的物体，滑轮与转轴之间的摩擦不计，滑轮与杆cd间的轻绳处于水平伸直状态并与导轨平行，导轨和金属细杆都处于匀强磁场中，磁场方向垂直于导轨所在平面向上，磁感应强度的大小为B，现两杆及悬物都从静止开始运动，当ab杆及cd杆的速度分别为v₁和v₂时，两杆加速度的大小各为多少？

【答案】

a₁＝\(\frac{{{B^2}{l^2}({v_2} - {v_1})}}{{2Rm}}\)，a₂＝\(\frac{{2Rm - {B^2}{l^2}({v_2} - {v_1})}}{{2R(M + m)}}\)

 

6．有一种高脚酒杯，如图所示，杯内底面为一凸起的球面，球心在顶点O下方玻璃中的C点，球面半径R＝1.50cm，O到杯口平面的距离为8.0cm，在杯脚中心处P点紧贴一张画片，P点距O点6.3cm，这种酒杯未斟酒时，若在杯口处向杯底方向观看，看不出画片上的景物，但如果斟了酒，再在杯口处向杯底方向观看，将看到画片上的景物。已知玻璃的折射率n₁＝1.56，酒的折射率为n₂＝1.34，试通过分析计算与论证解释这一现象。

 

【答案】

第21届全国预赛6

 

7．如图所示，B是质量为m_B、半径为R的光滑半球形碗，放在光滑的水平桌面上，A是质量为m_A的细长直杆，被固定的光滑套管C约束在竖直方向，A可自由上下运动，碗和杆的质量关系为：m_A＝2m_B，初始时，A杆被握住，使其下端正好与碗的半球面的上边缘接触（如图），然后从静止开始释放A，A、B便开始运动，设A杆的位置用θ表示，θ为碗面的球心O至A杆下端与球面接触点的连线方向和竖直方向之间的夹角，求A与B速度的大小（表示成θ的函数）。

【答案】

v_A＝\(\sqrt {\frac{{2gR\cos \theta }}{{1 + 2{{\cot }^2}\theta }}} \)，

v_B＝\(\sqrt {\frac{{2gR\cos \theta }}{{2 + {{\tan }^2}\theta }}} \)。

 

8．如图所示的电路中，各电源的内阻均为零，其中B、C两点与其右方由1.0Ω的电阻和2.0Ω的电阻构成的无穷组合电路相接，求图中10μF的电容器与E点相接的极板上的电荷量。

【答案】

Q₃＝1.3×10^-4C，是负电

 

9．如图所示，定滑轮B、C与动滑轮D组成一个滑轮组，各滑轮与转轴间的摩擦、滑轮的质量均不计，在动滑轮D上，悬挂有砝码托盘A，跨过滑轮组的不可伸长的轻线的两端各挂有砝码2和砝码3，一根用轻线（图中穿过弹簧的那条竖直线）拴住的压缩轻弹簧竖直放置在托盘底上，弹簧的下端与托盘底固连，上端放有砝码1（两者未粘连），已知三个砝码和砝码托盘的质量都是m，弹簧的劲度系数为k，压缩量为l₀，整个系统处在静止状态，现突然烧断拴住弹簧的轻线，弹簧便伸长，并推动砝码1向上运动，直到砝码1与弹簧分离，假设砝码1在以后的运动过程中不会与托盘的顶部相碰，求砝码1从与弹簧分离至再次接触经历的时间。

【答案】

t＝\(\frac{{2\sqrt {\frac{{3(kl_0^2 - 2mg{l_0})}}{{4m}}} }}{g}\)