1．卢瑟福通过对 α 粒子散射实验结果的分析，提出了原子内部存在（    ）

（A）电子     （B）中子     （C）质子     （D）原子核

【答案】

D

 

2．一束单色光由空气进入水中，则该光在空气和水中传播时（    ）

（A）速度相同，波长相同        （B）速度不同，波长相同

（C）速度相同，频率相同        （D）速度不同，频率相同

【答案】

D

 

3．各种不同频率范围的电磁波按频率由大到小的排列顺序是（    ）

（A）γ 射线、紫外线、可见光、红外线

（B）γ 射线、红外线、紫外线、可见光

（C）紫外线、可见光、红外线、γ 射线

（D）红外线、可见光、紫外线、γ 射线

【答案】

A

 

4．如图，顶端固定着小球的直杆固定在小车上，当小车向右做匀加速运动时，球所受合外力的方向沿图中的（    ）

（A）OA 方向                                  （B）OB 方向

（C）OC 方向                                  （D）OD 方向

【答案】

D

 

5．磁铁在线圈中心上方开始运动时，线圈中产生如图方向的感应电流，则磁铁（    ）

（A）向上运动                          （B）向下运动

（C）向左运动                          （D）向右运动

【答案】

B

 

6．放射性元素 A 经过 2 次 α 衰变和 1 次 β 衰变后生成一新元素 B，则元素 B 在元素周期表中的位置较元素 A 的位置向前移动了（    ）

（A）1 位             （B）2 位             （C）3 位             （D）4 位

【答案】

C

 

7．在今年上海的某活动中引入了全国首个户外风洞飞行体验装置，体验者在风力作用下漂浮在半空。若减小风力，体验者在加速下落过程中（    ）

（A）失重且机械能增加                   （B）失重且机械能减少

（C）超重且机械能增加                   （D）超重且机械能减少

【答案】

B

 

8．如图，一束电子沿 z 轴正向流动，则在图中 y 轴上 A 点的磁场方向是（    ）

（A）＋ x 方向                           （B）− x 方向

（C）＋ y 方向                           （D）− y 方向

【答案】

A

 

9．在双缝干涉实验中，屏上出现了明暗相间的条纹，则（    ）

（A）中间条纹间距较两侧更宽

（B）不同色光形成的条纹完全重合

（C）双缝间距离越大条纹间距离也越大

（D）遮住一条缝后屏上仍有明暗相间的条纹

【答案】

D

 

10．研究放射性元素射线性质的实验装置如图所示。两块平行放置的金属板 A、B 分别与电源的两极 a、b 连接，放射源发出的射线从其上方小孔向外射出。则（    ）

（A）a 为电源正极，到达 A 板的为 α 射线

（B）a 为电源正极，到达 A 板的为 β 射线

（C）a 为电源负极，到达 A 板的为 α 射线

（D）a 为电源负极，到达 A 板的为 β 射线

【答案】

B

 

11．国际单位制中，不是电场强度的单位是（    ）

（A）N/C             （B）V/m             （C）J/C              （D）T·m/s

【答案】

C

 

12．如图，粗细均匀的玻璃管 A 和 B 由一橡皮管连接，一定质量的空气被水银柱封闭在 A 管内，初始时两管水银面等高，B 管上方与大气相通。若固定 A 管，将 B 管沿竖直方向缓慢下移一小段距离 H，A 管内的水银面高度相应变化 h，则（    ）

（A）h ＝ H                                （B）h ＜ $\frac{H}{2}$

（C）h ＝ $\frac{H}{2}$                              （D）$\frac{H}{2}$ ＜ h ＜ H

【答案】

B

 

13．电源电动势反映了电源把其它形式的能量转化为电能的能力，因此（    ）

（A）电动势是一种非静电力

（B）电动势越大，表明电源储存的电能越多

（C）电动势的大小是非静电力做功能力的反映

（D）电动势就是闭合电路中电源两端的电压

【答案】

C

 

14．物体做匀加速直线运动，相继经过两段距离均为 16m 的路程，第一段用时 4 s，第二段用时 2 s，则物体的加速度是（    ）

（A）$\frac{2}{3}$ m/s²         （B）$\frac{4}{3}$ m/s²         （C）$\frac{8}{9}$ m/s²         （D）$\frac{16}{9}$ m/s²

【答案】

B

 

15．如图，始终竖直向上的力 F 作用在三角板 A 端，使其绕 B 点在竖直平面内缓慢地沿顺时针方向转动一小角度，力 F 对 B 点的力矩为 M，则转动过程中（    ）

（A）M 减小，F 增大               （B）M 减小，F 减小

（C）M 增大，F 增大                （D）M 增大，F 减小

【答案】

A

 

16．风速仪结构如图（a）所示。光源发出的光经光纤传输，被探测器接收，当风轮旋转时，通过齿轮带动凸轮圆盘旋转，当圆盘上的凸轮经过透镜系统时光被遮挡。已知风轮叶片转动半径为 r，每转动 n 圈带动凸轮圆盘转动一圈。若某段时间 Δt 内探测器接收到的光强随时间变化关系如图（b）所示，则该时间段内风轮叶片（    ）

（A）转速逐渐减小，平均速率为 $\frac{4\pi nr}{\mathrm{\Delta }t}$

（B）转速逐渐减小，平均速率为 $\frac{8\pi nr}{\mathrm{\Delta }t}$

（C）转速逐渐增大，平均速率为 $\frac{4\pi nr}{\mathrm{\Delta }t}$

（D）转速逐渐增大，平均速率为 $\frac{8\pi nr}{\mathrm{\Delta }t}$

【答案】

B

 

17．某气体的摩尔质量为 M，分子质量为 m。若 1 摩尔该气体的体积为 V_m，密度为 ρ，则该气体单位体积分子数为（阿伏伽德罗常数为 N_A）（    ）

（A）$\frac{N_{\mathrm{A}}}{V_{\mathrm{m}}}$             （B）$\frac{M}{m{V}_{\mathrm{m}}}$           （C）$\frac{\rho N_{\mathrm{A}}}{M}$           （D）$\frac{\rho N_{\mathrm{A}}}{m}$

【答案】

ABC

 

18．如图所示电路中，电源内阻忽略不计。闭合电键，电压表示数为 U，电流表示数为 I；在滑动变阻器 R₁ 的滑片 P 由 a 端滑到 b 端的过程中（    ）

（A）U 先变大后变小

（B）I 先变小后变大

（C）U 与 I 比值先变大后变小

（D）U 变化量与 I 变化量比值等于 R₃

【答案】

BC

 

19．如图（a），螺线管内有平行于轴线的外加匀强磁场，以图中箭头所示方向为其正方向。螺线管与导线框 abcd 相连，导线框内有一小金属圆环 L，圆环与导线框在同一平面内。当螺线管内的磁感应强度 B 随时间按图（b）所示规律变化时（    ）

（A）在 t₁ ～ t₂ 时间内，L 有收缩趋势

（B）在 t₂ ～ t₃ 时间内，L 有扩张趋势

（C）在 t₂ ～ t₃ 时间内，L 内有逆时针方向的感应电流

（D）在 t₃ ～ t₄ 时间内，L 内有顺时针方向的感应电流

【答案】

AD

 

20．甲、乙两列横波在同一介质中分别从波源 M、N 两点沿 x 轴相向传播，波速为 2 m/s，振幅相同；某时刻的图像如图所示。则（    ）

（A）甲乙两波的起振方向相反

（B）甲乙两波的频率之比为 3∶2

（C）再经过 3 s，平衡位置在 x ＝ 7m 处的质点振动方向向下

（D）再经过 3 s，两波源间（不含波源）有 5 个质点位移为零

【答案】

ABD

【解析】

甲、乙两列波起振方向一下一上，故 A 正确；

λ_甲 = 4 m，λ_乙 = 6 m，在同种介质中机械波波速相同，频率 f = $\frac{v}{\lambda }$，故 f_甲∶f_乙 = 3∶2，故 B 正确；

再经过 3 s，甲、乙波都传播 6 m，x = 7 m 处，甲波在波谷处，乙波在 x 轴上方向上振动但不在波峰处，故该质点振动方向向上，故 C 错误；

画出波形图，由波的叠加可知两波源间有 5 个质点位移为 0，故 D 正确。

 

 

21．形象描述磁场分布的曲线叫做____________，通常___________的大小也叫做磁通量密度。

【答案】

磁感线；磁感应强度

 

22．如图，粗糙水平面上，两物体 A、B 以轻绳相连，在恒力 F 作用下做匀速运动。某时刻轻绳断开，A 在 F 牵引下继续前进，B 最后静止。则在 B 静止前，A 和 B 组成的系统动量_________（选填：“守恒”或“不守恒”）；在 B 静止后，A 和 B 组成的系统动量______（选填：“守恒”或“不守恒”）。

【答案】

守恒；不守恒

 

22．两颗卫星绕地球运行的周期之比为 27∶1，则它们的角速度之比为________，轨道半径之比为_________。

【答案】

1∶27；9∶1

 

23．如图，圆弧形凹槽固定在水平地面上，其中 ABC 是位于竖直平面内以 O 为圆心的一段圆弧，OA 与竖直方向的夹角为 α。一小球以速度 v₀ 从桌面边缘 P 水平抛出，恰好从 A 点沿圆弧的切线方向进入凹槽。小球从 P 到 A 的运动时间为____________；直线 PA 与竖直方向间夹角 β＝_________。

 

【答案】

$\frac{v_0\tan \alpha }{g}$；arctan（2cotα）

【解析】

无

 

24．如图，质量为 m 的带电小球 A 用绝缘细线悬挂于 O 点，处于静止状态。施加一水平向右的匀强电场后，A 向右摆动，摆动的最大角度为 60°，则 A 受到的电场力大小为______。在改变电场强度的大小和方向后，小球A的平衡位置在 α ＝ 60° 处，然后再将 A 的质量改变为 2m，其新的平衡位置在 α ＝ 30° 处，A 受到的电场力大小为______。

【答案】

$\frac{\sqrt{3}}{3}$mg；mg

 

25．地面上物体在变力F作用下由静止开始竖直向上运动，力 F 随高度 x 的变化关系如图所示，物体能上升的最大高为 h，h ＜ H。当物体加速度最大时其高度为______，加速度的最大值为_______。

【答案】

0 或 h；$\frac{gh}{2H-h}$

【解析】

由力 F 关于高度 x 线性变化可知加速度 a 也随高度 x 线性变化，因为物体从静止开始运动且最后速度为 0，故在运动中间位置 a = 0，且各点加速度大小关于此点对称，故最高点最低点加速度最大，物体所在高度为 0 或 h；

由图像可知外力 F = F₀ − $\frac{F_0}{H}$x；在最低点 F₀ – mg = ma，在最高点 F = F₀ − $\frac{F_0}{H}$h，mg – F = ma，解方程得 a = $\frac{gh}{2H-h}$。

 

26．在“用 DIS 研究机械能守恒定律”的实验中，用到的传感器是_______传感器。若摆锤直径的测量值大于其真实值会造成摆锤动能的测量值偏_________。（选填：“大”或“小”）。

【答案】

光电门；大

 

27．在“用多用电表测电阻、电流和电压”的实验中 

（1）（多选题）用多用电测电流或电阻的过程中

（A）在测量电阻时，更换倍率后必须重新进行调零

（B）在测量电流时，更换量程后必须重新进行调零

（C）在测量未知电阻时，必须先选择倍率最大挡进行试测

（D）在测量未知电流时，必须先选择电流最大量程进行试测

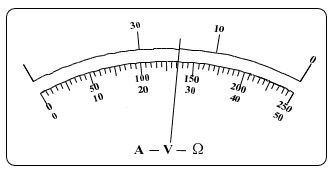（2）测量时多用电表指针指在如图所示位置。若选择开关处于“10 V”挡，其读数为________V；若选择开关处于“×10”挡，其读数为_______200 Ω（选填：“大于”，“等于”或“小于”）。

【答案】

（1）AD

（2）5.4；小于

 

28．“用 DIS 描绘电场的等势线”的实验装置示意图如图所示。

（1）（单选题）该实验描绘的是

（A）两个等量同种电荷周围的等势线

（B）两个等量异种电荷周围的等势线

（C）两个不等量同种电荷周围的等势线

（D）两个不等量异种电荷周围的等势线

（2）（单选题）实验操作时，需在平整的木板上依次铺放

（A）导电纸、复写纸、白纸                   （B）白纸、导电纸、复写纸

（C）导电纸、白纸、复写纸                   （D）白纸、复写纸、导电纸

（3）若电压传感器的红、黑探针分别接触图中 d、f 两点（f、d 连线与 A、B 连线垂直）时，示数小于零。为使示数为零，应保持红色探针与 d 点接触，而将黑色探针________（选填：“向左”或“向右”）移动。

【答案】

（1）B

（2）D

（3）向右

 

29．某同学制作了一个结构如图（a）所示的温度计。一端封闭的轻质细管可绕封闭端 O 自由转动，管长 0.5 m。将一量程足够大的力传感器调零，细管的开口端通过细线挂于力传感器挂钩上，使细管保持水平、细线沿竖直方向。在气体温度为 270 K 时，用一段水银将长度为 0.3 m 的气柱封闭在管内。实验时改变气体温度，测得封闭气柱长度l和力传感器读数 F 之间的关系如图（b）所示（实验中大气压强不变）。

（1）管内水银柱长度为______m，为保证水银不溢出，该温度计能测得的最高温度为_______K。

（2）若气柱初始长度大于 0.3 m，该温度计能测量的最高温度将________（选填：“增大”，“不变”或“减小”）。

（3）若实验中大气压强略有升高，则用该温度计测出的温度将________（选填：“偏高”，“不变”或“偏低”）。

【答案】

（1）0.1；360

（2）减小

（3）偏低

 

30．如图，两端封闭的直玻璃管竖直放置，一段水银将管内气体分隔为上下两部分 A 和 B，上下两部分气体初温度相等，且体积 V_A ＞ V_B。

（1）若 A、B 两部分气体同时升高相同的温度，水银柱将如何移动？

某同学解答如下：

设两部分气体压强不变，由

$\frac{V_1}{T_1}$ ＝ $\frac{V_2}{T_2}$，…，ΔV ＝ $\frac{\mathrm{\Delta }T}{T}$V，…，所以水银柱将向下移动。

上述解答是否正确？若正确，请写出完整的解答；若不正确，请说明理由并给出正确的解答。

（2）在上下两部分气体升高相同温度的过程中，水银柱位置发生变化，最后稳定在新的平衡位置，A、B 两部分气体始末状态压强的变化量分别为 Δp_A 和 Δp_B，分析并比较二者的大小关系。

【答案】

（1）不正确。

水银柱移动的原因是升温后，由于压强变化造成受力平衡被破坏，因此应该假设气体体积不变，由压强变化判断移动方向。

水银柱向上移动。

（2）Δp_A ＝ Δp_B

【解析】

（1）不正确。

水银柱移动的原因是升温后，由于压强变化造成受力平衡被破坏，因此应该假设气体体积不变，由压强变化判断移动方向。

正确解法：设升温后上下部分气体体积不变，则由查理定律可得

$\frac{p}{T}$ ＝ $\frac{p^{\prime }}{T+\mathrm{\Delta }T}$

Δp = pʹ − p = p

因为 ΔT > 0，p_A < p_B，可知 Δp_A < Δp_B，所以水银柱向上移动。

（2）升温前有      p_B = p_A + p_h（p_h 为汞柱压强）

升温后同样有        p_Bʹ = p_Aʹ + p_h

两式相减可得        Δp_A = Δp_B

 

31．风洞是研究空气动力学的实验设备。如图，将刚性杆水平固定在风洞内距地面高度 H ＝ 3.2 m 处，杆上套一质量 m ＝ 3 kg，可沿杆滑动的小球。将小球所受的风力调节为 F ＝ 15 N，方向水平向左。小球以速度 v₀ ＝ 8 m/s 向右离开杆端，假设小球所受风力不变，取 g ＝ 10 m/s²。求：

（1）小球落地所需时间和离开杆端的水平距离；

（2）小球落地时的动能。

（3）小球离开杆端后经过多少时间动能为 78 J？

【答案】

（1）t ＝ 0.8 s

s ＝ 4.8 m

（2）E_kt ＝ 120 J

（3）t₁ ＝0.4 s，t₂ ＝ 0.24 s

【解析】

（1）小球在竖直方向做自由落体运动，运动时间为

t ＝ $\sqrt{\frac{2H}{g}}$ ＝ 0.8 s

小球在水平方向做匀减速运动，加速度

a ＝ $\frac{F}{m}$ ＝ 5 m/s²

水平位移       s ＝ v₀t − $\frac{1}{2}$at² ＝ 4.8 m

（2）由动能定理  mgH − Fs ＝ E_kt − E_k0

E_kt ＝ 120 J

（3）小球离开杆后经过时间t的水平位移

s ＝ v₀t − $\frac{1}{2}$at²

由动能定理    mg·$\frac{1}{2}$gt² − Fs ＝ E_k − $\frac{1}{2}$mv₀²

以 E_k ＝ 78 J 和 v₀ ＝ 8 m/s 代入得

125t² − 80t + 12 ＝ 0

解得       t₁ ＝ 0.4 s，t₂ ＝ 0.24 s

 

32．如图（a），长度 L ＝ 0.8 m 的光滑杆左端固定一带正电的点电荷A，其电荷量 Q ＝ 1.8×10⁻⁷ C；一质量 m ＝ 0.02 kg，带电量为 q 的小球 B 套在杆上。将杆沿水平方向固定于某非均匀外电场中，以杆左端为原点，沿杆向右为 x 轴正方向建立坐标系。点电荷 A 对小球 B 的作用力随 B 位置 x 的变化关系如图（b）中曲线 Ⅰ 所示，小球 B 所受水平方向的合力随 B 位置 x 的变化关系如图（b）中曲线 Ⅱ 所示，其中曲线 Ⅱ 在 0.16 ≤ x ≤ 0.20 和 x ≥ 0.40 范围可近似看作直线。求：（静电力常量 k ＝ 9×10⁹ N·m²/C²）

（1）小球 B 所带电量 q；

（2）非均匀外电场在 x ＝ 0.3 m 处沿细杆方向的电场强度大小 E；

（3）在合电场中，x ＝ 0.4 m 与 x ＝ 0.6 m 之间的电势差 U。

（4）已知小球在 x ＝ 0.2 m 处获得 v ＝ 0.4 m/s 的初速度时，最远可以运动到 x ＝ 0.4 m 处。若小球在 x ＝ 0.16 m 处受到方向向右，大小为 0.04 N 的恒力作用后，由静止开始运动，为使小球能离开细杆，恒力作用的最小距离 s 是多少？

【答案】

（1）q ＝ 1×10⁻⁶ C

（2）E ＝ 3×10⁴ N/C

方向水平向左。

（3）U ＝ 800 V

（4）s ＝ 0.065 m

【解析】

（1）由图可知，当 x = 0.3 m 时，F₁ = k$\frac{qQ}{x^2}$ = 0.018 N

因此        q = \(\frac{{{F_1}{x^2}}}{{kQ}}\ = 1×10⁻⁶ C

（2）设在 x = 0.3 m 处点电荷与小球间作用力为 F₂，

F_合 = F₂ + qE

因此        E = $\frac{F_{合}-F_2}{q}$＝$\frac{-0.012-0.018}{1\times {10}^{-6}}$N/C = − 3×10⁴ N/C

电场在 x = 0.3 m 处沿细杆方向的电场强度大小为 3×10⁴ N/C，方向水平向左。

（3）根据图像可知在 x = 0.4 m 与 x = 0.6 m 之间合力做功大小

W_合 = 0.004×0.2 J = 8×10⁻⁴ J

由 qU = W_合

可得        U = $\frac{W_{合}}{q}$ = 800 V

（4）由图可知小球从 x = 0.16 m 到 x = 0.2 m 处

电场力做功    W₁ = $\frac{0.03\times 0.04}{2}$ J = 6×10⁻⁴ J

小球从 x = 0.2 m 到 x = 0.4 m 处

电场力做功    W₂ = − $\frac{1}{2}$mv² = − 1.6×10⁻³ J

由图可知小球从 x = 0.4 m 到x = 0.8 m 处

电场力做功    W₃ = − 0.004×0.4 J = − 1.6×10⁻³ J

由动能定理    W₁ + W₂ + W₃ + F_外s = 0

解得        s = − $\frac{W+W+W}{F_{外}}$ = 0.065 m

 

33．如图，一关于 y 轴对称的导体轨道位于水平面内，磁感应强度为 B 的匀强磁场与平面垂直。一足够长，质量为 m 的直导体棒沿 x 轴方向置于轨道上，在外力 F 作用下从原点由静止开始沿 y 轴正方向做加速度为 a 的匀加速直线运动，运动时棒与 x 轴始终平行。棒单位长度的电阻为 ρ，与电阻不计的轨道接触良好，运动中产生的热功率随棒位置的变化规律为 P ＝ ky^3/2（SI）。求：

（1）导体轨道的轨道方程 y ＝ f（x）；

（2）棒在运动过程中受到的安培力 F_m 随 y 的变化关系；

（3）棒从 y ＝ 0 运动到 y ＝ L 过程中外力 F 的功。

【答案】

（1）y ＝（$\frac{4a{B}^2}{k\rho }$）²x²

轨道形状为抛物线。

（2）F_m ＝ $\frac{k}{\sqrt{2a}}$y

（3）W ＝ $\frac{k}{2\sqrt{2a}}$L² ＋ maL

【解析】

（1）设棒运动到某一位置时与轨道接触点的坐标为（±x，y），安培力的功率

F ＝ $\frac{B^2{l}^{2}v}{R}$

P ＝ $\frac{4B^2{x}^2{v}^2}{R}$＝ky^3/2

棒做匀加速运动

v² ＝ 2ay

R ＝ 2ρx

代入前式得    y ＝（$\frac{4a{B}^2}{k\rho }$）²x²

轨道形状为抛物线。

（2）安培力         F_m ＝ $\frac{4B^2{x}^2}{R}$v＝$\frac{2B^{2}x}{\rho }\sqrt{2ay}$

以轨道方程代入得

F_m ＝ $\frac{k}{\sqrt{2a}}$y

（3）由动能定理         W ＝ W_m ＋ $\frac{1}{2}$mv²

由（2）结论可知安培力与位移成线性关系，所以安培力做功           W_m ＝ $\frac{k}{2\sqrt{2a}}$L²

棒在 y ＝ L 处动能         $\frac{1}{2}$mv² ＝ maL

外力做功                     W ＝ $\frac{k}{2\sqrt{2a}}$L² ＋ maL