1．下列关于光的说法中正确的是（    ）

（A）在真空中红光波长比紫光波长短

（B）红光光子能量比紫光光子能量小

（C）红光和紫光相遇时能产生干涉现象

（D）红光照射某金属时有电子向外发射，紫光照射该金属时一定也有电子向外发射

【答案】

BD

 

2．关于α、β、γ三种射线，下列说法中正确的是（    ）

（A）α射线是原子核自发放射出的氦核，它的穿透能力最强

（B）β射线是原子核外电子电离形成的电子流，它具有中等的穿透能力

（C）γ射线一般伴随着α或β射线产生，它的穿透能力最强

（D）γ射线是电磁波，它的穿透能力最弱

【答案】

C

【解析】

无

 

3．一小球用轻绳悬挂在某固定点，现将轻绳水平拉直，然后由静止开始释放小球，考虑小球由静止开始运动到最低位置的过程中（      ）

（A）小球在水平方向的速度逐渐增大

（B）小球在竖直方向的速度逐渐增大

（C）到达最低位置时小球线速度最大

（D）到达最低位置时绳中的拉力等于小球重力

【答案】

AC

 

4．如图所示，两根平行放置的长直导线a和b载有大小相同方向相反的电流，a受到的磁场力大小为F₁，当加入一与导线所在平面垂直的匀强磁场后，a受到的磁场力大小变为F₂，则此时b受到的磁场力大小变为（     ）

（A）F₂    （B）F₁－F₂    （C）F₁＋F₂    （D）2F₁－F₂

【答案】

A

【解析】

无

 

5．行驶中的汽车制动后滑行一段距离，最后停下；流星在夜空中坠落并发出明亮的光焰；降落伞在空中匀速下降；条形磁铁在下落过程中穿过闭合线圈，线圈中产生电流，上述不同现象中所包含的相同的物理过程是（     ）

（A）物体克服阻力做功

（B）物体的动能转化为其它形式的能量

（C）物体的势能转化为其它形式的能量

（D）物体的机械能转化为其它形式的能量

【答案】

AD

 

6．匀速上升的升降机顶部悬殊有一轻质弹簧，弹簧下端挂有一小球，若升降机突然停止，在地面上的观察者看来，小球在继续上升的过程中（        ）

（A）速度逐渐减小    （B）速度先增大后减小

（C）加速度逐渐增大    （D）加速度逐渐减小

【答案】

AC

 

7．如图，沿波的传播方向上有间距均为1 m的六个质点a、b、c、d、e、f，均静止在各自的平衡位置，一列横波以1 m/s的速度水平向右传播，t＝0时到达质点a，a开始由平衡位置向上运动，t＝1 s时，质点a第一次到达最高点，则在4 s＜t＜5 s这段时间内（       ）

（A）质点c的加速度逐渐增大    （B）质点a的速度逐渐增大

（C）质点d向下运动    （D）质点f保持静止

【答案】

ACD

【解析】

无

 

8．如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球，支架悬挂在O点，可绕过O点并与支架所在平面相垂直的固定轴转动，开始时OB与地面相垂直，放手后开始运动，在不计任何阻力的情况下，下列说法正确的是（        ）

（A）A球到达最低点时速度为零

（B）A球机械能减少量等于B球机械能增加量

（C）B球向左摆动所能达到的最高位置应高于A球开始运动时的高度

（D）当支架从左向右回摆动时，A球一定能回到起始高度

【答案】

BCD

 

9．两木块自左向右运动，现用高速摄影机在同一底片上多次曝光，记录下木块每次曝光时的位置，如图所示，连续两次曝光的时间间隔是相等的。由图可知（     ）

（A）在时刻t₂以及时刻t₅两木块速度相同

（B）在时刻t₁两木块速度相同

（C）在时刻t₃和时刻t₄之间某瞬间两木块速度相同

（D）在时刻t₄和时刻t₅之间某瞬时两木块速度相同

【答案】

C

 

10．如图（a），圆形线圈P静止在水平桌面上，其正上方悬挂一相同的线圈Q，P和Q共轴，Q中通有变化电流，电流随时间变化的规律如图（b）所示，P所受的重力为G，桌面对P的支持力为N，则（           ）

（A）t₁时刻N＞G

（B）t₂时刻N＞G

（C）t₃时刻N＜G

（D）t₄时刻N＝G

【答案】

AD

 

11．如图，在场强为E的匀强电场中有相距为l的A、B两点，边线AB与电场线的夹角为θ，将一电量为q的正电荷从A点移到B点，若沿直线AB移动该电荷，电场力做的功W₁＝____________；若沿路径ACB移动该电荷，电场力做的功W₂＝________；若沿曲线ADB移动该电荷，电场力做的功W₃＝___________，由此可知，电荷在电场中移动时，电场力做功的特点是：______________________。

【答案】

qElcosθ，qElcosθ，qElcosθ ，电场力做功的大小与路径无关，只与始末位置有关。

【解析】

无

 

12．一架飞机水平匀速地在某同学头顶飞过，当他听到飞机的发动机声从头顶正上方传来时，发现飞机在他前上方约与地面与60°角的方向上，所此可估算出此飞机的速度约为声速的____________倍。

【答案】

0.58（或\(\frac{{\sqrt 3 }}{3}\)）

 

13．右图为人手臂面骨骼与肌肉的生理结构示意图，手上托着重量为G的物体，

（1）在方框中画出前臂受力示意图（手、手腕、尺骨和挠骨看成一个整体，所受重力不计，图中O点看作固定转动轴，O点受力可以不画）。

（2）根据图中标尺估算出二头肌此时的收缩力约为_______。

【答案】

（1）如图

（2）8G

【解析】

无

 

14．某脉冲激光器的耗电功率为 2×10³ W，每秒钟输出 10 个光脉冲，每个脉冲持续的时间为 10^-8 s，携带的能量为 0.2 J，则每个脉冲的功率为___________W，该激光器将电能转化为激光能量的效率为__________。

【答案】

2×10⁷，0.001

 

15． 右图为一名宇航员“漂浮”在地球外层空间的照片，根据照片展现的情景提出两个与物理知识有关的问题（所提的问题可以涉及力学、电磁学、热学、光学、原子物理学等各个部分，只需提出问题，不必作出回答和解释）：例：这名“漂浮”在空中的宇航员相对地球是运动还是静止的？

（1）___________________________________________。

（2）___________________________________________。

【答案】

只要属于与照片情景有关的物理问题均可得分，例如：此宇航员是否受地球引力作用？此宇航员受力是否平衡？宇航员背后的天空为什么是黑暗的？等等，若解答不以问题的形式出现、不属于物理问题或与照片情景无关，均不能得分。

 

16．右图为用频闪摄影方法拍摄的研究物体作平抛运动规律的照片，图中A、B、C为三个同时由同一点出发的小球，AA′为A球在光滑水平面上以速度v运动的轨迹；BB′为B球以速度v被水平抛出后的运动轨迹；CC′为C球自由下落的运动轨迹，通过分析上述三条轨迹可得出结论：_________________________。

【答案】

作平抛运动的物体在水平方向作匀速直线运动，在竖直方向作自由落体运动（或平抛运动是水平方向的匀速直线运动和竖直方向的自由落体运动的合成）。

【解析】

无

 

17．单色光源发出的光经一狭缝，照射到光屏上，可观察到的图象是（          ）

【答案】

A

 

18．用右图所示装置做“研究有固定转动轴物体平衡条件”的实验，力矩盘上各同心圆的间距相等。

（1）在用细线悬挂钩码前，以下哪些措施是必要的（         ）

（A）判断力矩盘是否处在竖直平面

（B）判断横杆MN是否严格保持水平

（C）判断力矩盘与转轴间的摩擦是否足够小

（D）判断力矩盘的重心是否位于盘中心

（2）在A、B、C三点分别用细线悬挂钩码后，力矩盘平衡，如图所示，已知每个钩码所受的重力为1牛，则此时弹簧秤示数为_______牛。

（3）现同时撤去B、C两处的钩码，而改用一根细线悬挂5牛的钩码，为使力矩盘仍然保持原平衡状态，且弹簧秤示数不变，试在图中用直线画出该细线在力矩盘上的悬挂位置。

【答案】

（1）ACD

（2）4

（3）见图（悬线在转轴右侧竖直方向与第二圆环相切，钩码不画不扣分）。

 

19．某同学按如图所示电路进行实验，实验时该同学将变阻器的触片P移到不同位置时测得各电表的示数如下表所示。

序号	A1示数（安）	A2示数（安）	V1示数（伏）	V2示数（伏）
1	0.60	0.30	2.40	1.20
2	0.44	0.32	2.56	0.48

将电压表内阻看作无限大，电流表内阻看作零。

（1）电路中ε，r分别为电源的电动势和内阻，R₁，R₂，R₃为定值电阻，在这五个物理量中，可根据上表中的数据求得的物理量是（不要求具体计算）_________。

（2）由于电路发生故障，发现两电压表示数相同了（但不为零），若这种情况的发生是由用电器引起的，则可能的故障原因是_______。

【答案】

（1）R₂，R₃，ε

（2）R_p短路或R₂断开

【解析】

无

 

20．现有一根粗细均匀长约40厘米，两端开口的玻璃管，内有一小段水柱，一个弹簧秤，一把毫米刻度尺，一小块橡皮泥，一个足够高的玻璃容器，内盛有冰和水的混合物，选用合适的器材，设计一个实验，估测当时的室内温度，要求：

（1）在右边方框中画出实验示意图；

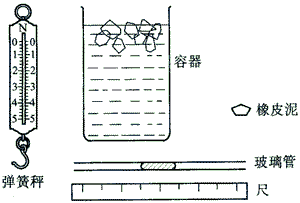
（2）写出要测定的物理量 ，写出可直接应用的物理量_______________，

（3）写出计算室温的表达式______________。

【答案】

（1）见下图

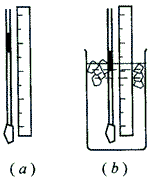
（2）玻璃管放在室温中时空气柱的长度l₁，玻璃管浸在冰水内时空气柱的长度l₂，冰水的温度T₀

（3）T＝\(\frac{{{l_1}}}{{{l_2}}}\)T₀

【解析】

无

 

21．风洞实验室中可以产生水平方向的、大小可调节的风力，现将一套有小球的细直杆放入风洞实验室，小球孔径略大于细杆直径。

（1）当杆在水平方向上固定时，调节风力的大小，使小球在杆上作匀速运动，这时小球所受的风力为小球所受重力的0.5倍，求小球与杆间的滑动摩擦因数。

（2）保持小球所受风力不变，使杆与水平方向间夹角为37°并固定，则小球从静止出发在细杆上滑下距离s所需时间为多少？（sin37°＝0.6，cos37°＝0.8）

【答案】

（1）0.5

（2）\(\sqrt {\frac{{8s}}{{3g}}} \)

【解析】

（1）设小球所受的风力为F，小球质量为m

F＝μmg

μ＝\(\frac{F}{{mg}}\)＝\(\frac{0.5mg}{{mg}}\)＝0.5

（2）设杆对小球的支持力为N，摩擦力为f

沿杆方向Fcosθ＋mgsinθ－f＝ma

垂直于杆方向N＋Fsinθ－mgcosθ＝0

f＝μN

可解得

a＝\(\frac{{F\cos \theta  + mg\sin \theta  - f}}{m}\)＝（g＋\(\frac{{{F^2}}}{{{m^2}g}}\)）sinθ＝\(\frac{3}{4}\)g

s＝\(\frac{1}{2}\)at²

t＝\(\sqrt {\frac{{2s}}{{\frac{3}{4}g}}} \)＝\(\sqrt {\frac{{8s}}{{3g}}} \) 

 

22．如图所示，粗细均匀，两端开口的U形管竖直放置，管的内径很小，水平部分BC长14 cm，一空气柱将管内水银分隔成左右两段，大气压强相当于高为76厘米水银柱的压强。

（1）当空气柱温度为T₀＝273 K，长为l₀＝8 cm时，BC管内左边水银柱长2 cm，AB管内水银柱长也是2 cm，则右边水银柱总长是多少？

（2）当空气柱温度升高到多少时，左边的水银恰好全部进入竖直管AB内？

（3）当空气柱温度为490 K时，两竖直管内水银柱上表面高度各为多少？

【答案】

（1）6 cm

（2）420 K

（3）右管内水银面高度为4 cm

左管内水银上表面高度为6 cm

【解析】

（1）U形管两端均开口，所以两竖直管内水银面高度应相同，即右边竖直管内水银柱高度为

h₀＝2 cm

右边水平管内水银柱长度为

14－l₀－2＝4c m

右边水银柱总长是

4＋2＝6 cm

（2）左边的水银全部进入竖直管内时，两竖直管内水银面高度均为

h₁＝4 cm

此时，右边水平管内水银柱长度为2 cm，所以空气柱长为

l₁＝14－2＝12 cm

\(\frac{{({p_0} + {h_0}){l_0}}}{{{T_0}}}\)＝\(\frac{{({p_0} + {h_1}){l_1}}}{{{T_1}}}\)

T₁＝\(\frac{{({p_0} + {h_1}){l_1}}}{{({p_0} + {h_0}){l_0}}}\)T₀＝\(\frac{{80 \times 12 }}{78 \times 8 }\)×273 K＝420 K

（3）设温度为T₂＝490 K时，空气柱长为l₂

等压过程  \(\frac{{{l_1}}}{{{T_1}}}\)=\(\frac{{{l_2}}}{{{T_2}}}\)

l₂＝\(\frac{{{l_1}}}{{{T_1}}}\)T₂＝\(\frac{12}{420}\)×490 cm＝14 cm

 

23．如图所示，固定水平桌面上的金属框架cdef，处在竖直向下的匀强磁场中，金属棒ab搁在框架上，可无摩擦滑动，此时adeb构成一个边长为l的正方形，棒的电阻为r，其余部分电阻不计，开始时磁感强度为B₀。

（1）若从t＝0时刻起，磁感强度均匀增加，每秒增量为k，同时保持棒静止，求棒中的感应电流，在图上标出感应电流的方向。

（2）在上述（1）情况中，始终保持棒静止，当t＝t₁秒末时需加的垂直于棒的水平拉力为多大？

（3）若从t＝0时刻起，磁感强度逐渐减小，当棒以恒定速度v向右作匀速运动时，可使棒中不产生感应电流，则磁感强度应怎样随时间变化（写出B与t的关系式）？

【答案】

（1）I＝\(\frac{{k{l^2}}}{r}\)

（2）F＝（B₀＋kt₁）\(\frac{{k{l^3}}}{r}\)

（3）B＝\(\frac{{{B_0}l}}{{l + vt}}\)

【解析】

（1）感应电动势E＝\(\frac{{\Delta \Phi }}{{\Delta t}}\)＝kl²

感应电流：I＝\(\frac{E}{r}\)＝\(\frac{{k{l^2}}}{r}\)

方向：逆时针（见图）

（2）t＝t₁秒时，B＝B₀＋kt₁

F＝BIL

F＝（B₀＋kt₁）\(\frac{{k{l^3}}}{r}\)

（3）总磁通量不变Bl（l＋vt）＝B₀l²

B＝\(\frac{{{B_0}l}}{{l + vt}}\)

 

24．阅读如下资料并回答问题：

自然界中的物体由于具有一定的温度，会不断向外辐射电磁波，这种辐射因与温度有关，称为热辐射，热辐射具有如下特点：

①辐射的能量中包含各种波长的电磁波；

②物体温度越高，单位时间从物体表面单位面积上辐射的能量越大；

③在辐射的总能量中，各种波长所占的百分比不同。

处于一定温度的物体在向外辐射电磁能量的同时，也要吸收由其他物体辐射的电磁能量，如果它处在平衡状态，则能量保持不变，若不考虑物体表面性质对辐射与吸收的影响，我们定义一种理想的物体，它能100%地吸收入射到其表面的电磁辐射，这样的物体称为黑体，单位时间内从黑体表面单位面积辐射的电磁波的总能量与黑体绝对温度的四次方成正比，即P₀＝σT⁴，其中常量σ＝5.67×10^-3 W/m²·K⁴。

在下面的问题中，把研究对象都简单地看作黑体。

有关数据及数学公式：太阳半径R_s＝696000 km，太阳表面温度T＝5770 K，火星半径r＝3395 km，球面积S＝4πR²，其中R为球半径。

（1）太阳热辐射能量的绝大多数集中在波长为2×10^-7 m～1×10^-5 m范围内，求相应的频率范围；

（2）每小量从太阳表面辐射的总能量为多少？

（3）火星受到来自太阳的辐射可认为垂直射可认为垂直身到面积为πr²（r为火星半径）的圆盘上，已知太阳到火星的距离约为太阳半径的400倍，忽略其它天体及宇宙空间的辐射，试估算火星的平均温度。

【答案】

（1）3×10¹³ Hz～1.5×10¹⁵ Hz

（2）W＝1.38×10¹⁰ J

（3）T′＝204 K

【解析】

（1）f＝\(\frac{c}{\lambda }\)

f₁＝\(\frac{{3.00 \times {{10}^8}}}{{2 \times {{10}^{ - 7}}}}\)Hz＝1.5×10¹⁵ Hz

f₂＝\(\frac{{3.00 \times {{10}^8}}}{{1 \times {{10}^{ - 5}}}}\)Hz＝3×10¹³ Hz

辐射的频率范围为3×10¹³ Hz～1.5×10¹⁵ Hz

（2）每小时从太阳表面辐射的总能量为

W＝4πσR_s²T⁴t

代入数所得W＝1.38×10¹⁰ J

（3）设火星表面温度为T，太阳到火星距离为d，火星单位时间内吸收来自太阳的辐射能量为

P_in＝4πσR_s²T⁴t·\(\frac{{\pi {r^2}}}{{4\pi {d^2}}}\)

d＝400R_s，

P_in＝\(\frac{{\pi \sigma {T^4}{r^2}}}{{{{400}^2}}}\)

火星单位时间内向外辐射电磁波能量为

P_out＝4πσr²T′⁴

火星处在平衡状态P_in＝P_out

即\(\frac{{\pi \sigma {T^4}{r^2}}}{{{{400}^2}}}\)＝4πσr²T′⁴

由上式解得火星平均温度T′＝\(\frac{T}{{\sqrt {800} }}\)＝204 K