1．国际单位制中，属于基本单位的是（    ）

（A）千克            （B）特斯拉        （C）牛顿            （D）库仑

【答案】

A

【解析】

 

 

2．下列各种射线中，属于电磁波的是（     ）

（A）α射线                （B）β射线                （C）γ射线                 （D）阴极射线

【答案】

C

【解析】

 

 

3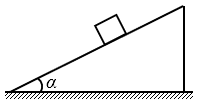．如图，质量为m的物体沿倾角为α的固定光滑斜面下滑，则物体对斜面压力的大小为（     ）

（A）mgsinα                （B）mgcosα

（C）mgtanα                （D）mgcotα

【答案】

B

【解析】

 

 

4．静电场的电场线（     ）

（A）可以相交                                        （B）是闭合的曲线

（C）起始于正电荷，终止于负电荷        （D）是点电荷在电场中运动的轨迹

【答案】

C

【解析】

 

 

5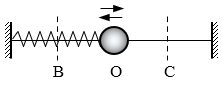．如图，O点为弹簧振子的平衡位置，小球在B、C间做无摩擦的往复运动。若小球从C点第一次运动到O点历时0.ls，则小球振动的周期为（    ）

（A）0.1s             （B）0.2s

（C）0.3s             （D）0.4s

【答案】

D

【解析】

 

 

6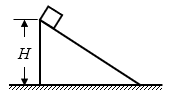．如图，一固定光滑斜面高为H，质量为m的小物体沿斜面从顶端滑到底端。在此过程（    ）

（A）物体的重力势能增加了mgH

（B）物体的重力势能减少了mgH

（C）重力对物体做的功大于mgH

（D）重力对物体做的功小于mgH

【答案】

B

【解析】

 

 

7．质量为2kg的质点仅受两个力作用，两个力的大小分别为16N和20N。则该质点加速度的最大值为（     ）

（A）2m/s²           （B）4m/s²           （C）18m/s²         （D）36m/s²

【答案】

C

【解析】

 

 

8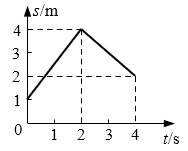．右图为一物体运动的s-t图像，在0到4s的时间内，该物体的位移为（     ）

（A）1m              （B）2m

（C）5m              （D）6m

【答案】

A

【解析】

 

 

9．某种气体在不同温度下的分子速率分布曲线如图所示，f(v) 表示分子速率v附近单位速率区间内的分子数百分率。曲线 Ⅰ 和 Ⅱ 所对应的温度分别为 T_Ⅰ 和 T_Ⅱ，所对应的气体分子平均动能分别为 E_k1 和 E_k2，则（      ）

（A）T_Ⅰ＞T_Ⅱ，E_k1＞E_k2            （B）T_Ⅰ＞T_Ⅱ，E_k1＜E_k2

（C）T_Ⅰ＜T_Ⅱ，E_k1＞E_k2            （D）T_Ⅰ＜T_Ⅱ，E_k1＜E_k2

【答案】

D

【解析】

 

 

10．质量为1kg的物体做自由落体运动，下落1s时重力的瞬时功率为（g取10m/s²）（   ）

（A）5W              （B）10W            （C）50W            （D）100W

【答案】

D

【解析】

 

 

11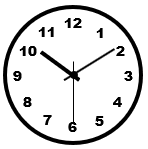．如图，时钟正常工作，比较时针、分针和秒针转动的角速度和周期，秒针的（    ）

（A）角速度最大，周期最大

（B）角速度最大，周期最小

（C）角速度最小，周期最大

（D）角速度最小，周期最小

【答案】

B

【解析】

 

 

12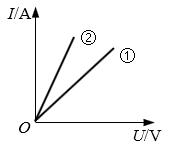．右图为电阻①和电阻②的I-U图像，两电阻的阻值分别为R₁和R₂。把两电阻串联后接入电路，通过它们的电流大小分别为I₁和I₂，则（     ）

（A）R₁＞R₂，I₁＝I₂          （B）R₁＜R₂，I₁＝I₂

（C）R₁＞R₂，I₁＜I₂          （D）R₁＜R₂，I₁＞I₂

【答案】

A

【解析】

 

 

13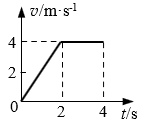．右图为一质点运动的v-t图像，则该质点在1s末的加速度和3s末的速度分别为（    ）

（A）4m/s²，4m/s       （B）2m/s²，2m/s

（C）2m/s²，4m/s        （D）4m/s²，2m/s

【答案】

C

【解析】

 

 

14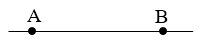．如图，水平直线表示电场中的一条电场线，A、B为电场线上的两点。一负点电荷仅在电场力作用下，从静止开始由A向B做匀加速运动。则从A到B，电场强度（    ）

（A）逐渐增大，方向向左        （B）保持不变，方向向左

（C）逐渐增大，方向向右        （D）保持不变，方向向右

【答案】

B

【解析】

 

 

15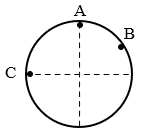．竖直墙上A、B、C三处各有一个水平细钉子，光滑圆环如图悬挂，圆环与三个钉子均有接触。A、B、C三点中，A在圆环的最高点，C与圆环的圆心等高，则圆环受到钉子的弹力情况是（     ）

（A）可能只有A处有               （B）可能只有A、B两处有

（C）一定只有B、C两处有      （D）A、B、C三处一定都有

【答案】

A

【解析】

对圆环进行受力分析，A、B、C、D四个选项的对应的受力分析图如下图（a）、（b）（c）、（d）所示：

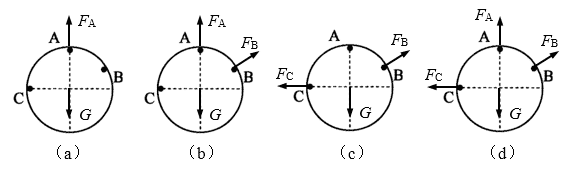
由（a）可以看出，圆环受到G和F_A两个力作用，两者等大反向一直线，符合平衡条件，所以选项A正确。图（b）显示圆环受到三个力作用，这三个力明显合力不为零，因此不可能受力平衡，选项B不正确。图（c）和图（d）的情况圆环都有可能静止，但并不是唯一的情况，因此选项C和D都是不正确的。

 

16．卢瑟福通过________实验，否定了汤姆孙的原子结构模型，提出了原子的_______结构模型。

【答案】

α粒子散射，核式

【解析】

 

 

17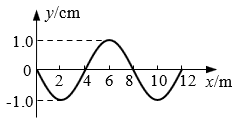．右图为一列横波在某一时刻的波形图，则该波的波长为_______m；若波速为2m/s，则该波的周期为_______s。

【答案】

8，4

【解析】

 

 

18．密闭在钢瓶中的气体，温度从27℃变为57℃，用热力学温标表示，温度升高了_____K，气体的压强变为原来的____倍。

【答案】

30，1.1

【解析】

 

 

19．A、B两质点相距为R，质量分别为m_A和m_B，且m_A＝3m_B。A受到B的万有引力大小为F_A，B受到A的万有引力大小为F_B，则F_A∶F_B＝________；若将它们之间的距离增大到2R，这时A受到B的万有引力大小为F_Aʹ，则F_A∶F_Aʹ＝_______。

【答案】

1∶1，4∶1

【解析】

 

 

20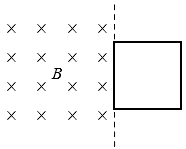．如图，面积S＝5.0×10^-4m²的正方形导线框处于磁感应强度B＝2.0×10^-3T的匀强磁场边缘，线框平面与磁场方向垂直。在线框向左进入磁场的过程中，线框中的感应电流为________（选填“顺时针”或“逆时针”）方向，穿过线框磁通量的最大值为_______Wb。

【答案】

逆时针，1.0×10^-6

【解析】

 

 

21．图（a）是流水线上的产品输送及计数装置示意图，其中S为光源，R₁为定值电阻，R₂为光敏电阻（无光照射时阻值大，有光照射时阻值小），电源电压恒为12V。产品随传送带匀速运动，当产品通过S与R₂之间时，射向R₂的光束会被挡住。合上电键K，R₂两端的电压随时间变化的关系如图（b）所示。则每分钟通过计数装置的产品个数为______个，有光照射和无光照射时R₂的功率之比为______。

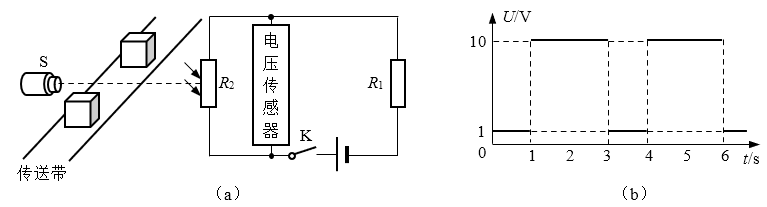
【答案】

20，11∶20

【解析】

 

 

22．如图，小球沿一竖直面内的光滑圆弧轨道下滑，O为圆心。画出小球在图示位置处的受力示意图。

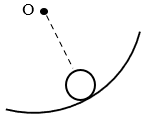
【答案】

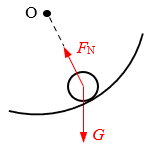
【解析】

 

 

22．如图，导体棒ab在匀强磁场中沿金属导轨运动时，产生的感应电流I到的方向从a到b，MN为螺线管中的一根磁感线。在图中画出：

①导体棒ab受到的磁场力的方向；

②磁感线MN的方向。

【答案】

【解析】

 

 

23．在练习使用多用表的实验中

（1）用多用表的欧姆档测量阻值R_x约为数十kΩ的电阻。以下是测量过程中的一些主要实验步骤：

a．将两表笔短接，调节欧姆档调零旋钮，使指针对准刻度盘上欧姆档的零刻度，然后断开两表笔

b．旋转选择开关至交流电压最大量程处（或“OFF”档），并拔出两表笔

c．旋转选择开关至欧姆档×1k

d．将两表笔分别连接到被测电阻的两端，读出阻值R_x，断开两表笔

以上实验步骤的正确顺序是________（填写步骤前的字母）。

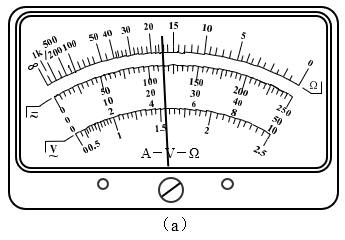实验中，多用表的指针位置如图（a）所示，则此被测电阻的阻值约为_____kΩ。

（2）为了较精确地测量另一定值电阻的阻值R_y，采用图（b）所示的电路。电源电压U恒定，电阻箱接入电路的阻值可调且能直接读出。

①用多用表测电路中的电流，则与a点相连的是多用表的____（选填“红”或“黑”）表笔。

②闭合电键，多次改变电阻箱阻值R，记录相应的R和多用表读数I，得到R-的关系如图（c）所示。则R_y＝______Ω，电源电压U＝____V。

【答案】

（1）cadb，17

（2）①红，②200，8

【解析】

 

 

24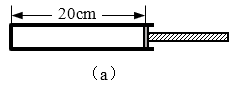．如图（a）所示，内壁光滑、粗细均匀、左端封闭的玻璃管水平放置。横截面积S＝2.0×10^-5m²的活塞封闭一定质量的气体，气柱长度l₀＝20cm，压强与大气压强相同。缓慢推动活塞，当气柱长度变为l＝5cm时，求：（大气压强p₀＝1.0×10⁵Pa，环境温度保持不变）

（1）玻璃管内气体的压强p；

（2）作用在活塞上的推力大小F。

（3）在图（b）中画出推动活塞过程中，气体经历的状态变化过程。

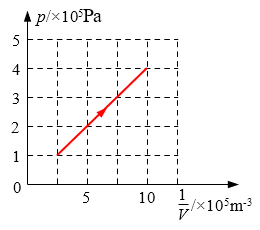
【答案】

（1）p＝4.0×10⁵ Pa

（2）F＝6 N

（3）管内气体变化过程如图所示

【解析】

（1）玻璃管内气体等温变化，由玻意耳定律         p₀V₀＝pV，

得                         p＝\(\frac{{{p_0}{V_0}}}{V}\)＝\(\frac{{{p_0}{l_0}}}{l}\)＝\(\frac{{1.0 \times {{10}^5} \times 0.2}}{{0.05}}\)Pa＝4.0×10⁵ Pa

（2）活塞受力平衡，p₀＋F＝pS

F＝（p－p₀）S＝（4.0×10⁵－1.0×10⁵）×2×10^-5 N＝6 N

（3）等温变化中p-\(\frac{1}{V}\)图线为过原点的倾斜直线。

 

25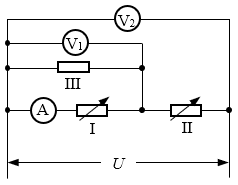．如图所示电路中，电源电压U恒定，Ⅰ和Ⅱ是电阻箱，Ⅲ是定值电阻。调节两电阻箱Ⅰ、Ⅱ的阻值R₁、R₂，但保持R₁与R₂之和不变，当R₁＝R₂时，安培表A的示数为0.4A，伏特表V₁和V₂的示数分别为4V和9V。求：

（1）R₁与R₂之和；

（2）定值电阻Ⅲ的阻值R₃。

（3）调节电阻箱的过程中，安培表A的示数会发生变化。分别求出安培表A的示数最大和最小时，电阻箱Ⅰ的阻值。

【答案】

（1）R₁＋R₂＝20Ω

（2）R₃＝40Ω

（3）当R₁＝0Ω或R₁＝20Ω时，安培表示数有最大值。

当R₁＝10Ω时，安培表示数有最小值。

【解析】

（1）在题设条件下，电阻箱Ⅰ的阻值为R₁＝\(\frac{{{U_1}}}{{{I_1}}} = \frac{4}{{0.4}}\)Ω＝10Ω

按题意有              R₂＝R₁＝10Ω

则                         R₁＋R₂＝20Ω

（2）通过电阻箱Ⅱ的电流I₂＝\(\frac{{{U_2} - {U_1}}}{{{R_2}}} = \frac{{9 - 4}}{{10}}\)A＝0.5A

通过定值电阻的电流           I₃＝I₂－I₁＝（0.5－0.4）A＝0.lA

定值电阻的阻值为              R₃＝\(\frac{{{U_1}}}{{{I_3}}} = \frac{4}{{0.1}}\)Ω＝40Ω

（3）当两个电阻箱阻值分别为R₁和R₂＝20－R₁时，设安培表的示数为I₁，有

\({I_1} = {I_总}\frac{{{R_3}}}{{{R_1} + {R_3}}} = \frac{{{U_2}}}{{\frac{{{R_1}{R_3}}}{{{R_1} + {R_3}}} + {R_2}}} \times \frac{{{R_3}}}{{{R_1} + {R_3}}} = \frac{{360}}{{ - R_1^2 + 20{R_1} + 800}} = \frac{{360}}{{ - {{({R_1} - 10)}^2} + 900}}\)

当R₁＝0Ω或R₁＝20Ω时，安培表示数有最大值。

当R₁＝10Ω时，安培表示数有最小值。

 

26．如图，ABC为一竖直面内的光滑轨道，AB段和BC段均为直线，且在B处平滑连接，AB段与水平面的夹角为37°。D、E是轨道上的两点，D点的高度h₁＝0.6m，E点的高度h₂＝0.2m。质量m＝1.6kg的小物体，受水平向左的恒力F的作用，从D点由静止开始，沿AB向下做匀加速直线运动。当物体运动到B点时撤去F，物体继续沿BC段斜向上运动，至E点时速度为零。求：（sin37°＝0.6，cos37°＝0.8，g取10m/s²）

（1）物体经过B点时的速率；

（2）物体所受恒力F的大小。

（3）在保持其他条件不变的前提下，F的大小变为4.8N：

①若物体在BC上运动的最大高度与D点的高度相同，求F的方向；

②若F取不同方向，则物体在BC上能达到不同的最大高度，求最大高度的取值范围。

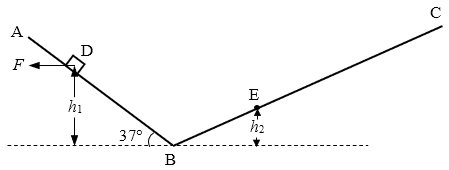
【答案】

（1）v_B＝2m/s

（2）F＝8N

（3）①F可以取垂直于AB向下或向上两个方向

②0.3m≤h≤0.9m

【解析】

（1）物体从B点到E点过程中机械能守恒

\(\frac{1}{2}\)mv_B²＝mgh₂

得：              v_B＝\(\sqrt {2g{h_2}}  = \sqrt {2 \times 10 \times 0.2} \)m/s＝2m/s                                  （3分）

（2）DB长   s＝\(\frac{{{h_1}}}{{\sin 37^\circ }} = \frac{{0.6}}{{0.6}}\)m＝1m

沿AB下滑的加速度大小           a＝\(\frac{{v_B^2}}{{2s}} = \frac{{{2^2}}}{{2 \times 1}}\)m/s²＝2m/s²

由牛顿第二定律：mgsin37°－Fcos37°＝ma

得：                     F＝\(\frac{{mg\sin 37^\circ  - ma}}{{\cos 37^\circ }} = \frac{{1.6 \times 10 \times 0.6 - 1.6 \times 2}}{{0.8}}\)N＝8N        （3分）

（3）

①因为物体在BC轨道上到达的最大高度与D点等高，可以断定：除重力做功之外，其他力不做功，即F不做功，F一定垂直于物体运动方向。因为F＜mgcos37°，F可以取垂直于AB向下或向上两个方向。

②（a）当F沿斜面向上时，物体的加速度最小，到达B点时的速度v_B1最小，在BC轨道上能到达的最大高度值最小。设此种情况下的加速度为a₁，由牛顿第二定律

mgsin37°－F＝ma₁，得a₁＝3m/s²，v_B1＝\(\sqrt {2{a_1}s}  = \sqrt {2 \times 3 \times 1} m/s = \sqrt 6 m/s\)，

物体在BC轨道上能到达的最大高度为            h_max1＝\(\frac{{v_{B1}^2}}{{2g}}\)＝0.3m。

（b）当F沿斜面向下时，物体的加速度最大，到达B点时的速度v_B2最大，在BC轨道上能到达的最大高度值最大。设此种情况下的加速度为a₂，由牛顿第二定律

mgsin37°＋F＝ma₂，得a₂＝9m/s²，v_B2＝\(\sqrt {2{a_2}s}  = \sqrt {2 \times 9 \times 1} m/s = 3\sqrt 2 m/s\)，

物体在BC轨道上能到达的最大高度为            h_max2＝\(\frac{{v_{B2}^2}}{{2g}}\)＝0.9m。

因此，物体在BC上能到达的最大高度范围是0.3m≤h≤0.9m。