1．横波传播

横波可沿一维介质或二维介质传播。

 

1．一列振幅为 A 的连续横波某时刻在 a、d 两介质点间的波形如图所示。其中 a、d 恰都位于平衡位置且相距 6 m，c 在波谷，该波的波速为 2 m/s，b 正向上振动。

（1）波长为_______m，波速方向水平向_______；

（2）abcd 四点中，此时加速度最大的是_______；

（3）（作图）在图中画出 4.5 s 后 ad 间的波形；

（4）若介质中同时有另一列振幅为 1.5A 的横波沿相反方向传播，且两波发生干涉，则另一列横波的频率应为_______，振动加强点的振幅为_______，振动减弱点的振幅为________。

 

2．如图所示为一列机械波经过某一分界面时同时发生反射和折射所形成的传播图样，若该波传播到图中①、②两点时的波速和振幅分别为 v₁、v₂ 和 A₁、A₂，则

A．v₁ > v₂，A₁ > A₂            B．v₁ > v₂，A₁ = A₂

C．v₁ > v₂，A₁ < A₂             D．v₁ < v₂，A₁ > A₂

E．v₁ < v₂，A₁ = A₂             F．v₁ < v₂，A₁ < A₂

【答案】

1．（1）4，右

（2）c 点

（3）如图

（4）0.5 Hz，2.5A，0.5A

2．A

 

2．等效替代

等效替代法是在保证某种效果相同的前提下，将实际的、复杂的物理问题和过程转化为等效的、简单的物理问题和过程来处理的方法。例如力以及运动的合成与分解，平均值的计算等都用到了这种方法。

 

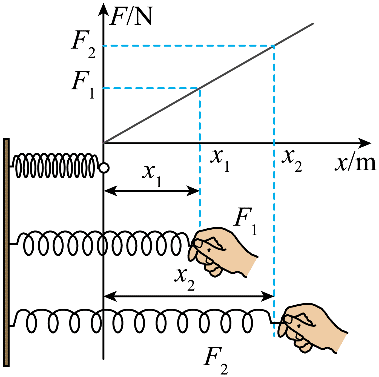1．如图所示为探究“弹簧弹性势能与形变量的关系”实验中测出的劲度系数为 k 的弹簧在不同拉力 F 作用下的伸长量 x 的 F–x 图像。

（1）拉伸弹簧的过程中，弹簧对手做_______功（选填“正”或“负”），弹簧弹性势能_______（选填“增加”或“减少”）。

（2）在计算变力做功的时候，可采用微元法或用平均力等效替代变力的方法。如图，将弹簧从伸长量为 x₁ 拉至 x₂ 的过程中，弹簧产生的平均弹力大小为_______，该弹力做功为_______，弹簧拉伸至 x₂ 时的弹性势能为_______。

 

2．（多选）两个大小分别为 F₁、F₂ 的作用力作用于图中一点，则合力

A．大小可能介于 F₁、F₂ 之间          B．大小一定大于 F₁ 或 F₂

C．方向可能在 F₁、F₂ 夹角外           D．方向一定在 F₁、F₂ 夹角内

 

3．（多选）两艘拖船 A、B 在平静海面上拖曳驳船 C 运动。图示时刻 A、B 的速度恰分别沿缆绳 CA、CB 方向。由于缆绳不可伸长，C 的速度在 CA、CB 方向的投影分别与 A、B 的速度相等，则此时 C 的速度

A．大小可以介于 A、B 的速度大小之间

B．大小一定不小于 A、B 的速度大小

C．方向可能在 CA 和 CB 的夹角范围外

D．方向一定在 CA 和 CB 的夹角范围内

【答案】

1．（1）负，增加

（2）\(\frac{1}{2}\)k(x₁ + x₂)，− \(\frac{1}{2}\)k(x₂² − x₁²)，\(\frac{1}{2}\)kx₂²

2．AD

3．BC

 

3．测量与探究

测量性实验与探究性实验是两种常见的实验类型。

 

1．某小组同学在“用单摆测量重力加速度的大小”实验中：

（1）测出单摆的摆长 L 及完成 n 次全振动所用的时间 t，可以推导出重力加速度 g = _______（用 L、n、t 表示）。

（2）实验中，当小球每次摆至最低点，此时小球所受的合外力

A．为零               B．指向运动方向               C．指向悬点方向

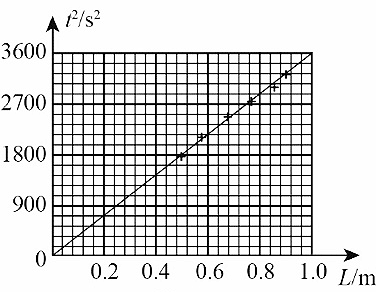（3）该小组同学多次调整摆长 L，并分别记录相应单摆完成 30 次全振动所用时间 t，处理数据绘出 t²–L 图像，如图所示。可以计算出当地的重力加速度 g = _______m/s²（计算结果保留三位有效数字）。

（4）经过长时间持续观测，单摆的振幅 A 随时间 t 变化的 A–t 图像应为

（5）若已测得当地的重力加速度 g。将一个摆长为L的单摆从平衡位置拉开很小的角度 θ 后静止释放，未测量其周期。忽略空气阻力，以平衡位置作为计时起点，则此摆球偏离平衡位置的位移 x 与时间 t 的关系式为_______。

 

2．另一组同学在“探究平抛运动特点”的实验中

（1）用图甲所示装置进行探究平抛运动的竖直分运动是否是自由落体运动。用摆锤击打弹性金属片，A 球水平抛出，B 球自由下落。关于该实验，下列操作中必要的是

A．两球的质量必须相等

B．需改变小球下落的高度多次实验

C．摆锤每次均在同一位置无初速度释放

（2）用如图乙所示装置做进一步探究。每次都将小球从斜槽轨道的同一位置无初速度释放，并从斜槽末端水平飞出。改变水平挡板的高度，测得小球在板上一系列落点位置的 x、y 值。以 x 为纵坐标，以_______为横坐标绘制图线，当图线为过原点的倾斜直线时，可证明小球做平抛运动的水平分运动为匀速直线运动。

【答案】

1．（1）\(\frac{{4{\pi ^2}{n^2}L}}{{{t^2}}}\)   （2）C

（3）9.86±0.01   （4）D

（5）Lsinθsin(\(\sqrt {\frac{g}{L}} \)∙t)

2．（1）B     （2）\(\sqrt y \) （答案不唯一）

 

4．篮球运动

篮球运动在校园中深受学生的喜爱。假定一个篮球质量为 m，重力加速度大小为 g。

 

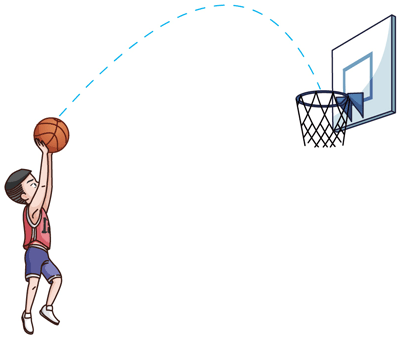1．篮球被投入篮筐中的运动轨迹如图所示。篮球出手和进入篮筐时的速度大小分别为 v₁ 和 v₂、离地高度分别为 h₁ 和 h₂，运动过程中离地最大高度为 H，空气阻力不可忽略。

（1）（作图）在图中分别画出篮球上升途经某点时速度 v 的方向和所受合外力 F 的方向。

（2）篮球从出手到进入篮筐过程中，损失的机械能为

A．\(\frac{1}{2}\)mv₁² − \(\frac{1}{2}\)mv₂²           B．\(\frac{1}{2}\)mv₂² − \(\frac{1}{2}\)mv₁²

C．mgh₂ − mgh₁                  D．\(\frac{1}{2}\)mv₁² − \(\frac{1}{2}\)mv₂² + mgh₁ – mgh₂

E．\(\frac{1}{2}\)mv₂² − \(\frac{1}{2}\)mv₁² + mgh₂ – mgh₁

（3）（多选）以出手点为零势能面，则篮球在最高点时的机械能一定

A．小于 \(\frac{1}{2}\)mv₁²                     B．大于 mgH

C．等于 mg(H − h₁)                   D．大于 \(\frac{1}{2}\)mv₂² + mg(h₂ – h₁)

 

2．将篮球从离地高度为 \(\frac{4}{5}\)H 处由静止释放，与地面的碰撞后反弹的最大高度为 H。若运动过程中篮球所受空气阻力 f  的大小近似不变，不计篮球碰撞地面的能量损失。求

（1）（计算）篮球所受空气阻力f的大小；

（2）（计算）运动员在篮球反弹至\(\frac{4}{5}\)H 高度时竖直向下拍打篮球，篮球与地面再次碰撞后恰能反弹至 H 高度。求运动员拍打篮球所做的功 W。

【答案】

1．（1）如图

（2）D

（3）AD

2．（1）f = \(\frac{1}{9}\)mg

（2）W = \(\frac{2}{5}\)mgh

 

5．汽车定位系统

如图所示为汽车在某段行驶过程中定位系统追踪定位的示意图，小圆点代表每隔 2.0 s 汽车所处的位置。汽车质量为 2000 kg，建立如图 x–y 平面直角坐标系。汽车在 AE 段做匀加速直线运动，其中 DE 段的长度为 32 m，汽车在 E 点的速度大小为 18 m/s。汽车直线运动过程中受到大小恒为 1000 N 的阻力。

 

1．汽车在 DE 段的平均速度大小为_______m/s；

2．汽车在 AE 段的加速度大小为_______m/s²；

3．汽车在 D 点牵引力的瞬时功率为_______kW；

4．（计算）行驶至 E 点时，司机突然提升汽车功率至 143 kW，求此时汽车的加速度的大小。（保留两位有效数字）

5．（计算）汽车从 E 点起以 143 kW 恒定功率驶过 EH 段，经过 H 点的速度大小为 32 m/s，求 EH 段的距离。

【答案】

1．16

2．2

3．70

4．a ≈ 3.5 m/s²

5．L = 158 m

 

6．三体问题

三体问题是指三个可视为质点的天体，在相互之间万有引力的作用下的运动规律问题，具有极大的难度，但当所讨论的三个天体质量相差悬殊时，则可大幅简化。

 

1．质量相同的两人造卫星 I、Ⅱ 分别沿轨道 m、n 绕地球做匀速圆周运动，运行轨迹如图。

（1）I、Ⅱ 运行周期 T₁_______T₂，与地球间的引力势能 E_p1_______E_p2（均选填“>”、“<”或“=”）。

（2）I、Ⅱ 运行时加速度的大小分别为 a₁、a₂，地球表面重力加速度大小为 g。则

A．g < a₁ < a₂              B．g < a₂ < a₁

C．a₁< a₂ < g               D．a₂ < a₁ < g

 

2．（计算）由于地球自转的影响，在地球表面不同的地方，物体的重量会随纬度的变化而有所不同。将地球视为质量均匀分布的球体，不考虑空气的影响。用弹簧秤称量一个相对于地面静止的小物体的重量，设在地球北极地面称量时，弹簧秤的读数是 F₁；在赤道地面称量时，弹簧秤的读数是 F₂。求在赤道地面，小物体随地球自转的向心力大小 F。

 

3．（计算）登月前，嫦娥五号在距离月球表面高为h处绕月球做匀速圆周运动，同时月球绕地球做匀速圆周运动，合成后可近似认为嫦娥五号绕地球运动的轨迹为等距螺旋线，如图所示。已知月球的轨道半径为 r，月球半径为 R，且 r ≫ R，地球、月球和嫦娥五号的质量为 m_地、m_月 和 m₀，引力常量为 G。嫦娥五号绕月球公转一周的时间内，沿月球公转方向运动的距离称为一个“螺距”，设公转向心力均仅由中心天体的引力提供。求嫦娥五号轨迹的“螺距”d。

【答案】

1．（1）<，<

（2）D

2．F = F₁ – F₂

3．d = \(\sqrt {\frac{{4{\pi ^2}{m_地}{{(R + h)}^3}}}{{{m_月}r}}} \)