1．2025 年 3 月，我国科学家研制的碳 14 核电池原型机“烛龙一号”发布，标志着我国在核能技术领域与微型核电池领域取得突破。碳 14 的衰变方程为 ¹⁴₆C→¹⁴₇N + X，则（    ）

A．X 为电子，是在核内中子转化为质子的过程中产生的

B．X 为电子，是在核内质子转化为中子的过程中产生的

C．X 为质子，是由核内中子转化而来的

D．X 为中子，是由核内质子转化而来的

【答案】

A

 

2．如图所示，中老铁路国际旅客列车从云南某车站由静止出发，沿水平直轨道逐渐加速到144 km/h，在此过程中列车对座椅上的一高中生所做的功最接近（    ）

A．4×10⁵ J                     B．4×10⁴ J

C．4×10³ J                     D．4×10² J

【答案】

B

【解析】

高中生的质量约为 50 kg，根据动能定理有 W = \(\frac{1}{2}\)mv² = 4×10⁴ J。

故选 B。

 

3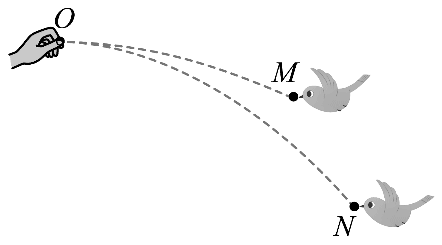．如图所示，某同学将两颗鸟食从 O 点水平抛出，两只小鸟分别在空中的 M 点和 N 点同时接到鸟食。鸟食的运动视为平抛运动，两运动轨迹在同一竖直平面内，则 （    ）

A．两颗鸟食同时抛出

B．在 N 点接到的鸟食后抛出

C．两颗鸟食平抛的初速度相同

D．在 M 点接到的鸟食平抛的初速度较大

【答案】

D

【解析】

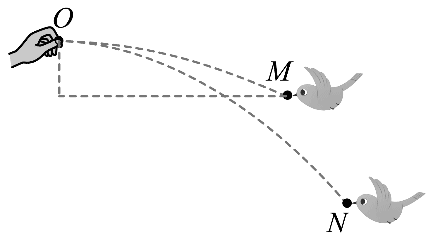AB．鸟食的运动视为平抛运动，则在竖直方向有 h = \(\frac{1}{2}\)gt²。

由于 h_M < h_N，则 t_M < t_N，要同时接到鸟食，则在 N 点接到的鸟食先抛出，故 AB 错误；

CD．在水平方向有 x = v₀t，如图所示，过 M 点作一水平面，可看出在相同高度处 M 点的水平位移大，则 M 点接到的鸟食平抛的初速度较大，故 C 错误，D 正确。

故选 D。

 

4．某介电电泳实验使用非匀强电场，该电场的等势线分布如图所示。a、b、c、d 四点分别位于电势为  – 2 V、− 1 V、1 V、2 V 的等势线上，则（    ）

A．a、b、c、d 中 a 点电场强度最小

B．a、b、c、d 中 d 点电场强度最大

C．一个电子从 b 点移动到 c 点电场力做功为 2 eV

D．一个电子从 a 点移动到 d 点电势能增加了 4 eV

【答案】

C

【解析】

AB．根据等势面越密集电场强度越大，可知 a、b、c、d 中 a 点电场强度最大，故 AB 错误；

C．一个电子从 b 点移动到 c 点电场力做功为 W_bc = − eU_bc = 2 eV

故 C 正确；

D．一个电子从 a 点移动到 d 点电场力做功为 W_ad = − eU_bc =  4 eV

由于电场力做正功电势能减小，则一个电子从 a 点移动到d点电势能减小了 4 eV，故 D 错误。

故选 C。

 

5．国际编号为 192391 的小行星绕太阳公转的周期约为 5.8 年，该小行星与太阳系内八大行星几乎在同一平面内做圆周运动。规定地球绕太阳公转的轨道半径为 1 AU，八大行星绕太阳的公转轨道半径如下表所示。忽略其它行星对该小行星的引力作用，则该小行星的公转轨道应介于（    ）

行星	水星	金星	地球	火星	木星	土星	天王星	海王星
轨道半径R/AU	0.39	0.72	1.0	1.5	5.2	9.5	19	30

A．金星与地球的公转轨道之间                 B．地球与火星的公转轨道之间

C．火星与木星的公转轨道之间                 D．天王星与海王星的公转轨道之间

【答案】

C

【解析】

根据开普勒第三定律可知 \(\frac{{r_行^3}}{{T_行^2}}\) = \(\frac{{r_地^3}}{{T_地^2}}\)。

其中 r_地 = 1 AU，T_地 = 1 年，T_行 = 5.8 年

代入解得 r_行 ≈ 3.23 AU

故可知该小行星的公转轨道应介于火星与木星的公转轨道之间。

故选 C。

 

6．如图所示，质量为 m 的滑块（视为质点）与水平面上 MN 段的动摩擦因数为 μ₁，与其余部分的动摩擦因数为 μ₂，且 μ₁ > μ₂。第一次，滑块从 I 位置以速度 v₀ 向右滑动，通过 MN 段后停在水平面上的某一位置，整个运动过程中，滑块的位移大小为 x₁，所用时间为 t₁；第二次，滑块从 Ⅱ 位置以相同速度 v₀ 向右滑动，通过 MN 段后停在水平面上的另一位置，整个运动过程中，滑块的位移大小为 x₂，所用时间为 t₂。忽略空气阻力，则（    ）

A．t₁ < t₂                B．t₁ > t₂                 C．x₁ > x₂                       D．x₁ < x₂

【答案】

A

【解析】

CD．对两种运动的整个过程根据能量守恒有

\(\frac{1}{2}\)mv₀² = μ₁mgx_MN + μ₂mg(x₁ − x_MN)，\(\frac{1}{2}\)mv₀² = μ₁mgx_MN + μ₂mg(x₂ − x_MN)

可得 x₁ = x₂，故 CD 错误；

AB．根据牛顿第二定律 μmg = ma

可得 a = μg

由于 μ₁ > μ₂，故滑块在 MN 上时的加速度大，根据前面分析可知两次运动的总位移相等，即两次运动过程中 v–t 图像与横轴围成的面积相等，由于第二次时滑块距离 M 点的距离较近，根据公式 v₀² – v² = 2μ₂gx 可知第二次到达 M 点时速度较大，作出整个过程中两种运动状态的 v–t 图像可得 t₁ < t₂，故 A 正确，B 错误；

故选 A。

 

7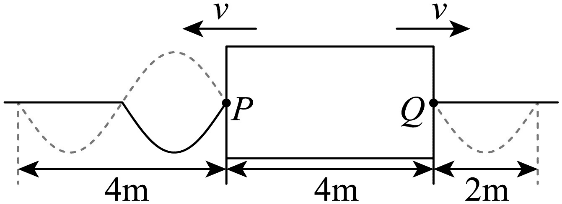．如图所示，均匀介质中矩形区域内有一位置未知的波源。t = 0 时刻，波源开始振动产生简谐横波，并以相同波速分别向左、右两侧传播，P、Q 分别为矩形区域左右两边界上振动质点的平衡位置。t = 1.5 s 和 t = 2.5 s 时矩形区域外波形分别如图中实线和虚线所示，则（    ）

A．波速为 2.5 m/s

B．波源的平衡位置距离 P 点 1.5 m

C．t = 1.0 s 时，波源处于平衡位置且向下运动

D．t = 5.5 s 时，平衡位置在 P、Q 处的两质点位移相同

【答案】

D

 

8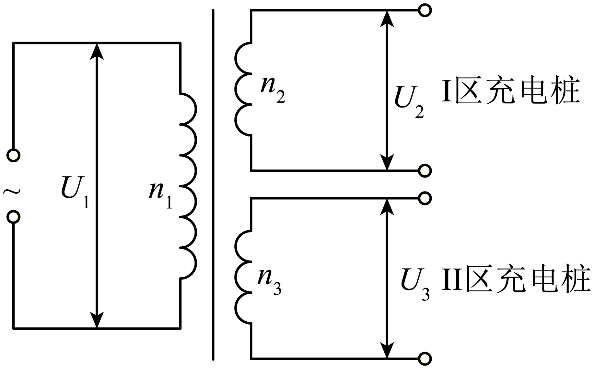．电动汽车充电桩的供电变压器（视为理想变压器）示意图如图所示。变压器原线圈的匝数为 n₁，输入电压 U₁ = 1.1 kV；两副线圈的匝数分别为 n₂ 和 n₃，输出电压 U₂ = U₃ = 220 V。当 I、Ⅱ 区充电桩同时工作时，两副线圈的输出功率分别为 7.0 kW 和 3.5 kW，下列说法正确的是（    ）

A．n₁∶n₂ = 5∶1

B．n₁∶n₃ = 1∶5

C．变压器的输入功率为 10.5 kW

D．两副线圈输出电压最大值均为 220 V

【答案】

AC

【解析】

AB．根据理想变压器的电压比等于匝数比可得 n₁∶n₂ = U₁∶U₂ = 5∶1，n₁∶n₃ = U₁∶U₃ = 5∶1。

故 A 正确，B 错误；

C．根据能量守恒可知变压器的输入功率等于总的输出功率，故

P_输入 = P_输出 = （7.0 + 3.5）kW = 10.5 kW

故 C 正确；

D．输出电压为交流电的有效值，根据正弦交流电的最大值与有效值的关系可知，两副线圈输出电压最大值均为 U_m = 220\(\sqrt 2 \) V

故 D 错误。

故选 AC。

 

9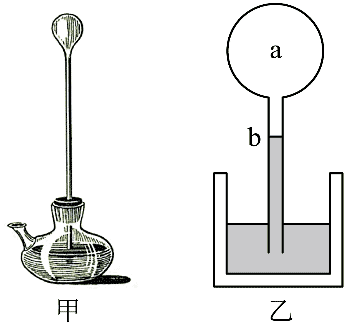．图甲为 1593 年伽利略发明的人类历史上第一支温度计，其原理如图乙所示。硬质玻璃泡 a 内封有一定质量的气体（视为理想气体），与 a 相连的 b 管插在水槽中固定，b 管中液面高度会随环境温度变化而变化。设 b 管的体积与 a 泡的体积相比可忽略不计，在标准大气压 p₀ 下，b 管上的刻度可以直接读出环境温度。则在 p₀ 下（    ）

A．环境温度升高时，b 管中液面升高

B．环境温度降低时，b 管中液面升高

C．水槽中的水少量蒸发后，温度测量值偏小

D．水槽中的水少量蒸发后，温度测量值偏大

【答案】

BD

【解析】

AB．根据题意，a 中气体做等容变化，根据查理定律可知，当环境温度升高，a 中气体压强增大，又 p_a + ρgh = p₀，可知 b 管中液面降低，同理可知环境温度降低时，b 管中液面升高，故 B 正确，A 错误；

CD．由 AB 选项分析可知，b 管中刻度从上到下温度逐渐升高，同一温度，a 中压强不变， b 管中液面液槽内液面高度差不变，水槽中的水少量蒸发后，槽中液面降低，则 b 管内液面降低，则温度测量值偏大，故 D 正确，C 错误。

故选 BD。

 

10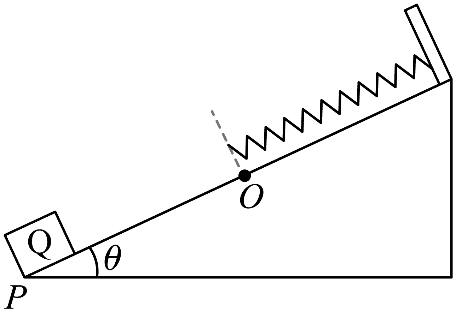．如图所示，倾角为 θ 的固定斜面，其顶端固定一劲度系数为 k 的轻质弹簧，弹簧处于原长时下端位于 O 点。质量为 m 的滑块 Q（视为质点）与斜面间的动摩擦因数 μ = tanθ。过程 Ⅰ：Q 以速度 v₀ 从斜面底端 P 点沿斜面向上运动恰好能滑至 O 点；过程 Ⅱ：将 Q 连接在弹簧的下端并拉至 P 点由静止释放，Q 通过 M 点（图中未画出）时速度最大，过 O 点后能继续上滑。弹簧始终在弹性限度内，假设最大静摩擦力等于滑动摩擦力，忽略空气阻力，重力加速度为 g。则（    ）

A．P、M 两点之间的距离为 \(\frac{{kv_0^2 - 4m{g^2}{{\sin }^2}\theta }}{{4kg\sin \theta }}\)

B．过程 Ⅱ 中，Q 在从 P 点单向运动到 O 点的过程中损失的机械能为 \(\frac{1}{4}\)mv₀²

C．过程 Ⅱ 中，Q 从 P 点沿斜面向上运动的最大位移为 \(\frac{{kv_0^2 - 8m{g^2}{{\sin }^2}\theta }}{{2kg\sin \theta }}\)

D．连接在弹簧下端的 Q 无论从斜面上何处释放，最终一定静止在 OM（含 O、M 点）之间

【答案】

BCD

 

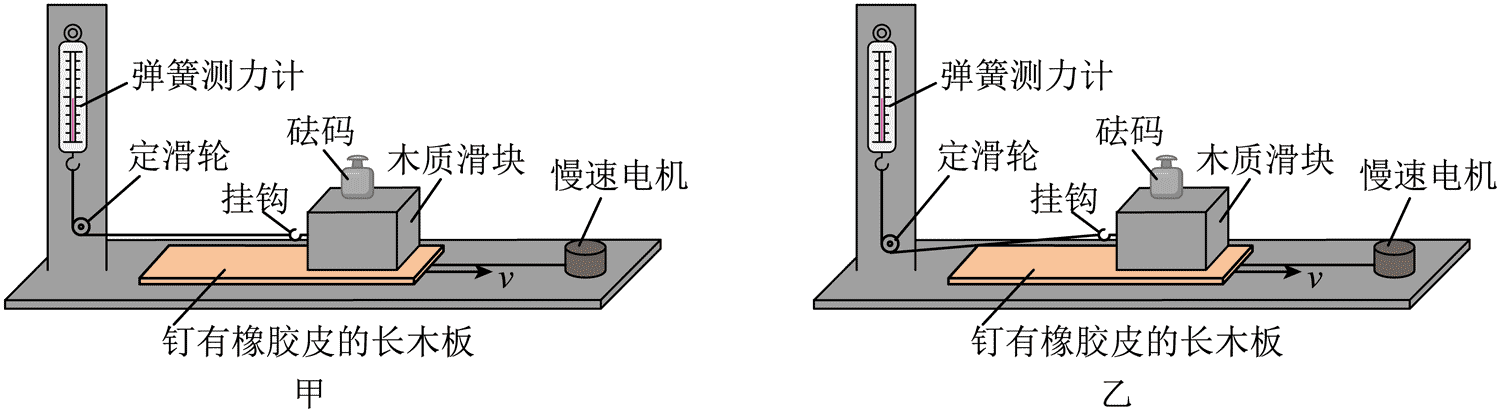
11．某实验小组做了测量木质滑块与橡胶皮之间动摩擦因数 μ 的实验，所用器材如下：钉有橡胶皮的长木板、质量为 250 g 的木质滑块（含挂钩）、细线、定滑轮、弹簧测力计、慢速电机以及砝码若干。实验装置如图甲所示。

实验步骤如下：

①将长木板放置在水平台面上，滑块平放在橡胶面上；

②调节定滑轮高度，使细线与长木板平行（此时定滑轮高度与挂钩高度一致）；

③用电机缓慢拉动长木板，当长木板相对滑块匀速运动时，记录弹簧测力计的示数F；

④在滑块上分别放置 50 g、100 g 和 150 g 的砝码，重复步骤③；

⑤处理实验数据（重力加速度 g 取 9.80 m/s²）。

实验数据如下表所示：

滑块和砝码的总质量 M/g	弹簧测力计示数 F/N	动摩擦因数 μ
250	1.12	0.457
300	1.35	a
350	1.57	0.458
400	1.79	0.457

完成下列填空：

（1）表格中 a 处的数据为________（保留 3 位有效数字）；

（2）其它条件不变时，在实验误差允许的范围内，滑动摩擦力的大小与接触面上压力的大小________，μ 与接触面上压力的大小________（以上两空填“成正比”“成反比”或“无关”）；

（3）若在实验过程中未进行步骤②，实验装置如图乙所示，挂钩高于定滑轮，则 μ 的测量结果将________（填“偏大”“偏小”或“不变”）。

【答案】

（1）0.459

（2）成正比，无关

（3）偏大

【解析】

（1）表格中 a 处的数据 μ = \(\frac{{1.35}}{{0.3 \times 9.8}}\) ≈ 0.459

（2）根据表中数据分析可知其它条件不变时，在实验误差允许的范围内，滑动摩擦力的大小与接触面上压力的大小成正比；

根据表中数据分析可知其它条件不变时，在实验误差允许的范围内，μ 与接触面上压力的大小无关。

（3）实验装置如图乙所示，挂钩高于定滑轮，则绳子拉力有竖直向下的分力，实际的正压力大于测量值的正压力，即 F_压测 < F_压实

根据 μ = \(\frac{F}{{{F_{压测}}}}\)

可得 μ_测 > μ_实

 

12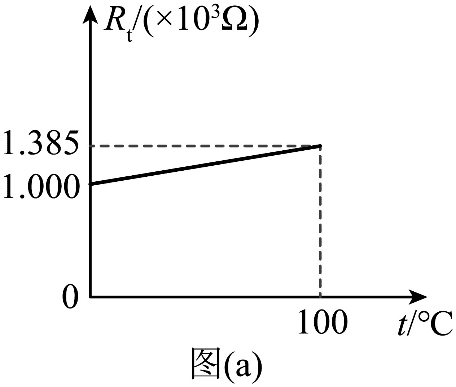．基于铂电阻阻值随温度变化的特性，某兴趣小组用铂电阻做了测量温度的实验。可选用的器材如下：Pt1000 型号铂电阻、电源 E（电动势 5 V，内阻不计）、电流表 A₁（量程 100 μA，内阻 4.5 kΩ）、电流表 A₂（量程 500 μA，内阻约 1 kΩ）、定值电阻 R₁（阻值 15 kΩ）、定值电阻 R₂（阻值 1.5 kΩ）、开关 S 和导线若干。

查阅技术手册可知，Pt1000 型号铂电阻测温时的工作电流在 0.1 ~ 0.3 mA 之间，在 0 ~ 100℃ 范围内，铂电阻的阻值 R_t 随温度 t 的变化视为线性关系，如图（a）所示。

完成下列填空：

（1）由图（a）可知，在 0 ~ 100℃ 范围内，温度每升高 1℃，该铂电阻的阻值增加________Ω；

（2）兴趣小组设计了如图（b）所示的甲、乙两种测量铂电阻阻值的电路图，能准确测出铂电阻阻值的是________（填“甲”或“乙”），保护电阻 R 应选________（填“R₁”或“R₂”）；

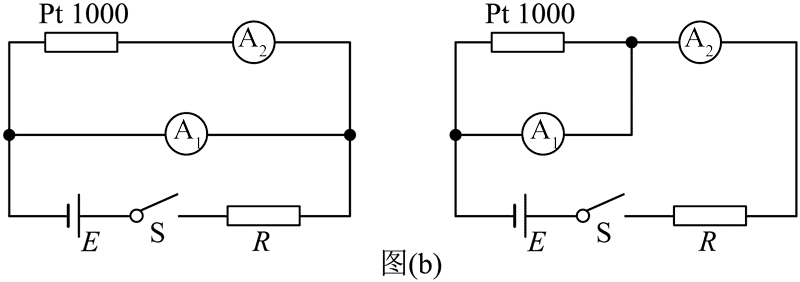
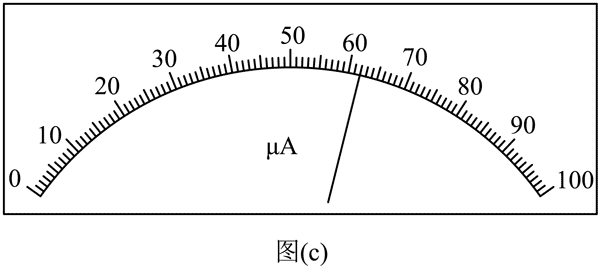
（3）用（2）问中能准确测出铂电阻阻值的电路测温时，某次测量读得 A₂ 示数为 295 μA，A₁ 示数如图（c）所示，该示数为________μA，则所测温度为________℃（计算结果保留 2 位有效数字）。

【答案】

（1）3.85

（2）乙，R₁

（3）62.0，51

 

13．用光学显微镜观察样品时，显微镜部分结构示意图如图甲所示。盖玻片底部中心位置 O 点的样品等效为点光源，为避免 O 点发出的光在盖玻片上方界面发生全反射，可将盖玻片与物镜的间隙用一滴油填充，如图乙所示。已知盖玻片材料和油的折射率均为 1.5，盖玻片厚度 d = 2.0 mm，盖玻片与物镜的间距 h = 0.20 mm，不考虑光在盖玻片中的多次反射，取真空中光速 c = 3.0×10⁸ m/s，π = 3.14。

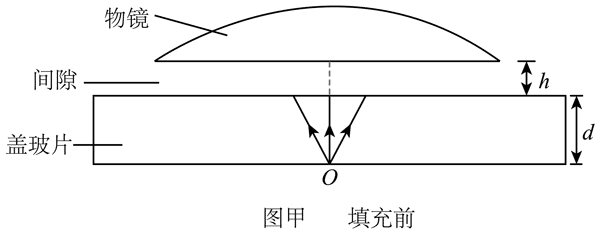
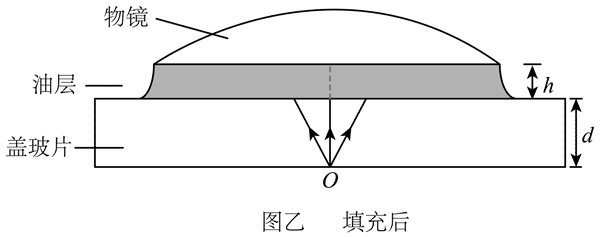
（1）求未滴油时，O 点发出的光在盖玻片的上表面的透光面积（结果保留 2 位有效数字）；

（2）滴油前后，光从 O 点传播到物镜的最短时间分别为 t₁、t₂，求 t₂ – t₁（结果保留 2 位有效数字）。

【答案】

（1）1.0×10^{− 5} m²

（2）3.3×10^{− 13} s

 

14．磁屏蔽技术可以降低外界磁场对屏蔽区域的干扰。如图所示，x ≥ 0 区域存在垂直 Oxy 平面向里的匀强磁场，其磁感应强度大小为 B₁（未知）。第一象限内存在边长为 2L 的正方形磁屏蔽区 ONPQ，经磁屏蔽后，该区域内的匀强磁场方向仍垂直 Oxy 平面向里，其磁感应强度大小为 B₂（未知），但满足 0 < B₂ < B₁。某质量为 m、电荷量为 q（q > 0）的带电粒子通过速度选择器后，在 Oxy 平面内垂直 y 轴射入 x ≥ 0 区域，经磁场偏转后刚好从 ON 中点垂直 ON 射入磁屏蔽区域。速度选择器两极板间电压 U、间距 d、内部磁感应强度大小 B₀ 已知，不考虑该粒子的重力。

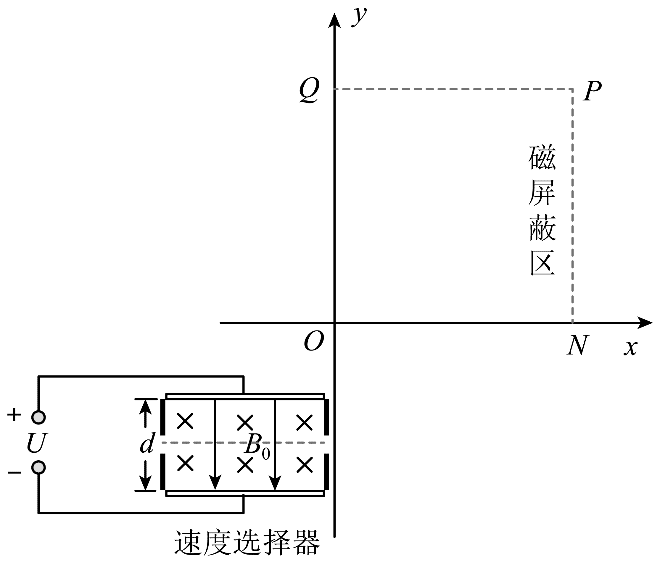
（1）求该粒子通过速度选择器的速率；

（2）求 B₁ 以及 y 轴上可能检测到该粒子的范围；

（3）定义磁屏蔽效率 η = \(\frac{{{B_1} - {B_2}}}{{{B_1}}}\)×100%，若在 Q 处检测到该粒子，则 η 是多少？

【答案】

（1）\(\frac{U}{{{B_0}d}}\)

（2）\(\frac{{mU}}{{qd{B_0}L}}\)，L < y < 3L

（3）60%

 

15．如图所示，光滑水平面上有一个长为 L、宽为 d 的长方体空绝缘箱，其四周紧固一电阻为 R 的水平矩形导线框，箱子与导线框的总质量为 M。与箱子右侧壁平行的磁场边界平面如截面图中虚线 PQ 所示，边界右侧存在范围足够大的匀强磁场，其磁感应强度大小为 B、方向竖直向下。t = 0 时刻，箱子在水平向右的恒力 F（大小未知）作用下由静止开始做匀加速直线运动，这时箱子左侧壁上距离箱底 h 处、质量为 m 的木块（视为质点）恰好能与箱子保持相对静止。箱子右侧壁进入磁场瞬间，木块与箱子分离；箱子完全进入磁场前某时刻，木块落到箱子底部，且箱子与木块均不反弹（木块下落过程中与箱子侧壁无碰撞）；木块落到箱子底部时即撤去 F。运动过程中，箱子右侧壁始终与磁场边界平行，忽略箱壁厚度、箱子形变、导线粗细及空气阻力。木块与箱子内壁间的动摩擦因数为 μ，假设最大静摩擦力等于滑动摩擦力，重力加速度为 g。

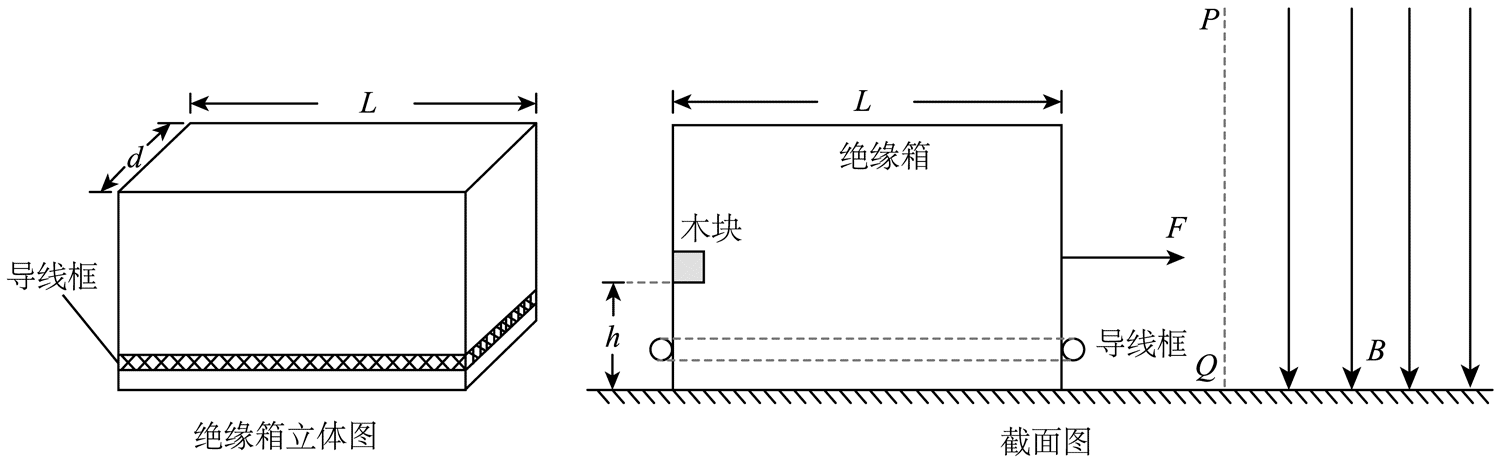
（1）求 F 的大小；

（2）求 t = 0 时刻，箱子右侧壁距磁场边界的最小距离；

（3）若 t = 0 时刻，箱子右侧壁距磁场边界的距离为 s（s 大于（2）问中最小距离），求最终木块与箱子的速度大小。

【答案】

（1）\(\frac{{(M + m)g}}{\mu }\)

（2）\(\frac{{{{(M + m)}^2}g{R^2}}}{{2\mu {B^4}{d^4}}}\)

（3）当 \(\frac{g}{\mu }\)（\(\sqrt {\frac{{2\mu s}}{g}} \) + \(\sqrt {\frac{{2h}}{g}} \)）≥ \(\frac{{{B^2}{d^2}L}}{{(M + m)R}}\) 时，最终木块与箱子的速度大小为

v =  \(\frac{g}{\mu }\)（\(\sqrt {\frac{{2\mu s}}{g}} \) + \(\sqrt {\frac{{2h}}{g}} \)）− \(\frac{{{B^2}{d^2}L}}{{(M + m)R}}\)

当 \(\frac{g}{\mu }\)（\(\sqrt {\frac{{2\mu s}}{g}} \) + \(\sqrt {\frac{{2h}}{g}} \)） < \(\frac{{{B^2}{d^2}L}}{{(M + m)R}}\) 时，最终木块与箱子的速度大小为 v = 0。