1．2025 年 4 月 30 日，神舟十九号载人飞船成功返回。某同学在观看直播时注意到，返回舱从高度 3 090 m 下降到高度 2 010 m，用时约 130 s。这段时间内，返回舱在竖直方向上的平均速度大小约为（    ）

A．8.3 m/s             B．15.5 m/s           C．23.8 m/s           D．39.2 m/s

【答案】

A

【解析】

返回舱下降的位移为 Δh = 1 080 m，则返回舱在竖直方向上的平均速度大小约为 v = \(\frac{{\Delta h}}{t}\) ≈ 8.3 m/s

故选 A。

 

2．某多晶薄膜晶格结构可以等效成缝宽约为 3.5×10⁻¹⁰ m的狭缝。下列粒子束穿过该多晶薄膜时，衍射现象最明显的是（    ）

A．德布罗意波长约为 7.9×10⁻¹³m 的中子

B．德布罗意波长约为 8.7×10⁻¹²m 的质子

C．德布罗意波长约为 2.6×10⁻¹¹m 的氮分子

D．德布罗意波长约为 1.5×10⁻¹⁰m 的电子

【答案】

D

【解析】

当波通过尺寸与其波长相近的障碍物或狭缝时，会发生明显的衍射现象。对于粒子而言，德布罗意波长 λ 决定了其波动性，衍射的明显程度通常与波长 λ 和狭缝宽度 d 的比值相关，当 λ/d 接近或大于 1 时，衍射现象非常明显，则可知电子的衍射现象最明显。

故选 D。

 

3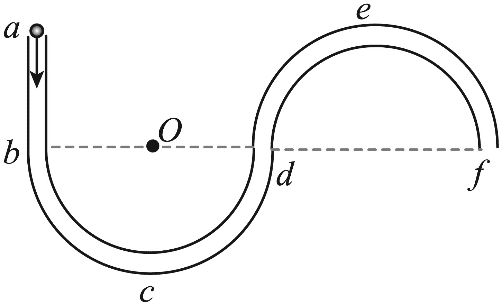．如图所示，由长为 R 的直管 ab 和半径为 R 的半圆形弯管 bcd、def 组成的绝缘光滑管道固定于水平面内，管道间平滑连接。bcd 圆心 O 点处固定一电荷量为 Q（Q > 0）的带电小球。另一个电荷量 为q（q > 0 且 q ≪ Q）的带电小球以一定初速度从 a 点进入管道，沿管道运动后从 f 点离开。忽略空气阻力。则（    ）

A．小球在 e 点所受库仑力大于在 b 点所受库仑力

B．小球从 c 点到 e 点电势能先不变后减小

C．小球过 f 点的动能等于过 d 点的动能

D．小球过 b 点的速度大于过 a 点的速度

【答案】

B

【解析】

A．小球所受库仑力 F = \(\frac{{kQq}}{{{r^2}}}\)

由于 r_e > r_b，则小球在 e 点所受库仑力小于在 b 点所受库仑力，故A错误；

B．点电荷在距其 r 处的电势为 φ = \(\frac{{kQ}}{r}\)

由于 c 点到 d 点 r 不变，d 点到 e 点 r 逐渐增大，则根据 E_p = φq

可知小球从 c 点到 d 点电势能不变，从 d 点到 e 点电势能逐渐减小，故B正确；

C．由于 r_f > r_d，根据选项 B 可知，小球的电势能 E_pd > E_pf，根据能量守恒可知，小球过 f 点的动能大于过 d 点的动能，故 C 错误；

D．由于 r_a > r_b，根据选项 B 可知，小球的电势能 E_pb > E_pa，根据能量守恒可知，小球过 a 点的动能大于过 b 点的动能，则小球过 b 点的速度小于过 a 点的速度，故 D 错误。

故选 B。

 

4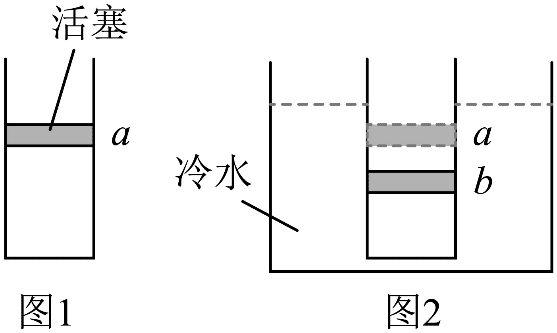．如图 1 所示，用活塞将一定质量的理想气体密封在导热气缸内，活塞稳定在 a 处。将气缸置于恒温冷水中，如图 2 所示，活塞自发从 a 处缓慢下降并停在 b 处，然后保持气缸不动，用外力将活塞缓慢提升回 a 处。不计活塞与气缸壁之间的摩擦。则（    ）

A．活塞从 a 到 b 的过程中，气缸内气体压强升高

B．活塞从 a 到 b 的过程中，气缸内气体内能不变

C．活塞从 b 到 a 的过程中，气缸内气体压强升高

D．活塞从 b 到 a 的过程中，气缸内气体内能不变

【答案】

D

【解析】

AB．根据题意可知活塞从 a 到 b 的过程中，气缸内气体，温度降低，则内能减小，体积减小，压强不变，故 AB 错误；

CD．根据题意可知活塞从 b 到 a 的过程中气缸内气体温度不变，则内能不变，体积增大，根据玻意耳定律可知压强减小，故 C 错误，D 正确。

故选 D。

 

5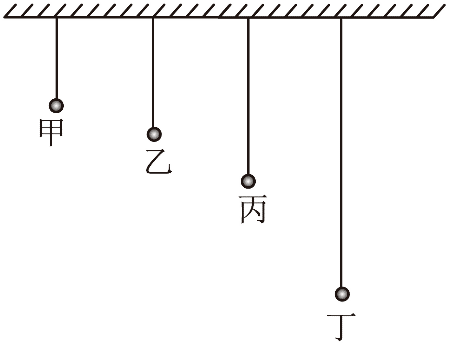．如图所示，甲、乙、丙、丁四个小球用不可伸长的轻绳悬挂在天花板上，从左至右摆长依次增加，小球静止在纸面所示竖直平面内。将四个小球垂直纸面向外拉起一小角度，由静止同时释放。释放后小球都做简谐运动。当小球甲完成 2 个周期的振动时，小球丙恰好到达与小球甲同侧最高点，同时小球乙、丁恰好到达另一侧最高点。则（    ）

A．小球甲第一次回到释放位置时，小球丙加速度为零

B．小球丁第一次回到平衡位置时，小球乙动能为零

C．小球甲、乙的振动周期之比为 3∶4

D．小球丙、丁的摆长之比为 1∶2

【答案】

C

 

6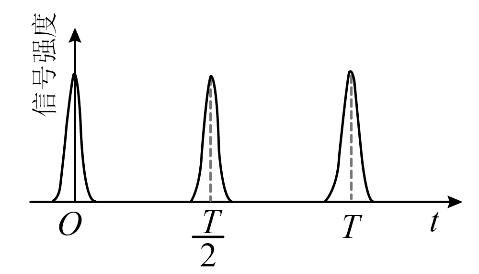．某人造地球卫星运行轨道与赤道共面，绕行方向与地球自转方向相同。该卫星持续发射信号，位于赤道的某观测站接收到的信号强度随时间变化的规律如图所示，T 为地球自转周期。已知该卫星的运动可视为匀速圆周运动，地球质量为 M，万有引力常量为 G。则该卫星轨道半径为（    ）

A．\(\sqrt[3]{{\frac{{GM{T^2}}}{{36{\pi ^2}}}}}\)               B．\(\sqrt[3]{{\frac{{GM{T^2}}}{{16{\pi ^2}}}}}\)                C．\(\sqrt[3]{{\frac{{GM{T^2}}}{{4{\pi ^2}}}}}\)                D．\(\sqrt[3]{{\frac{{9GM{T^2}}}{{4{\pi ^2}}}}}\)

【答案】

A

 

7．如图所示，倾角为 30° 的光滑斜面固定在水平地面上，安装在其顶端的电动机通过不可伸长轻绳与小车相连，小车上静置一物块。小车与物块质量均为 m，两者之间动摩擦因数为 \(\frac{{\sqrt 3 }}{2}\)。电动机以恒定功率 P 拉动小车由静止开始沿斜面向上运动。经过一段时间，小车与物块的速度刚好相同，大小为 v₀。运动过程中轻绳与斜面始终平行，小车和斜面均足够长，重力加速度大小为 g，忽略其他摩擦。则这段时间内（   ）

A．物块的位移大小为 \(\frac{{2v_0^2}}{{3g}}\)                          B．物块机械能增量为 \(\frac{5}{2}\)mv₀²

C．小车的位移大小为 \(\frac{{16P{v_0}}}{{5m{g^2}}}\) − \(\frac{{2v_0^2}}{{5g}}\)          D．小车机械能增量为 \(\frac{{8P{v_0}}}{{5g}}\) + \(\frac{1}{2}\)mv₀²

【答案】

C

 

8．若长度、质量、时间和动量分别用 a、b、c 和 d 表示，则下列各式可能表示能量的是（    ）

A．\(\frac{{{a^2}b}}{{{c^2}}}\)          B．\(\frac{{a{b^2}}}{{{c^2}}}\)          C．\(\frac{{{d^2}}}{b}\)            D．\(\frac{{{b^2}}}{d}\)

【答案】

AC

 

9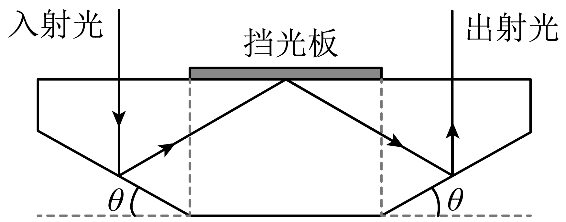．某款国产手机采用了一种新型潜望式摄像头模组。如图所示，模组内置一块上下表面平行（θ < 45°）的光学玻璃。光垂直于玻璃上表面入射，经过三次全反射后平行于入射光射出。则（    ）

A．可以选用折射率为 1.4 的光学玻璃

B．若选用折射率为 1.6 的光学玻璃，θ 可以设定为 30°

C．若选用折射率为 2 的光学玻璃，第二次全反射入射角可能为 70°

D．若入射光线向左移动，则出射光线也向左移动

【答案】

CD

【解析】

A．因为 1.4 < \(\sqrt 2 \)，故当选用折射率为 1.4 的光学玻璃时，根据 sinC = \(\frac{1}{n}\)

可知 sinC > \(\frac{{\sqrt 2 }}{2}\)，即 C > 45°

根据几何知识可知光线第一次发生全反射时的入射角为 θ < 45° < C，故选用折射率为 1.4 的光学玻璃时此时不会发生全反射，故 A 错误；

B．当 θ = 30° 时，此时入射角为 30°，选用折射率为 1.6 的光学玻璃时，此时的临界角为

sinC = \(\frac{1}{{1.6}}\) = 0.625 > 0.5 = sin30°

故 C > 30°，故此时不会发生全反射，故 B 错误；

C．若选用折射率为 2 的光学玻璃，此时临界角为 sinC = \(\frac{1}{{2}}\)

即 C > 30°，此时光线第一次要发生全反射，入射角一定大于 30°，即第一次发生全反射时的入射光线和反射光线的夹角一定大于 60°，根据几何关系可知第一次发生全反射时的入射光线和反射光线的夹角等于第二次全反射入射角，故可能为 70°，故 C 正确；

D．若入射光线向左移动，可知第一次全反射时的反射光线向左移动，第二次全反射时的反射光线向左移动，同理，第三次全反射时的反射光线向左移动，即出射光线向左移动，故 D 正确。

故选 CD。

 

10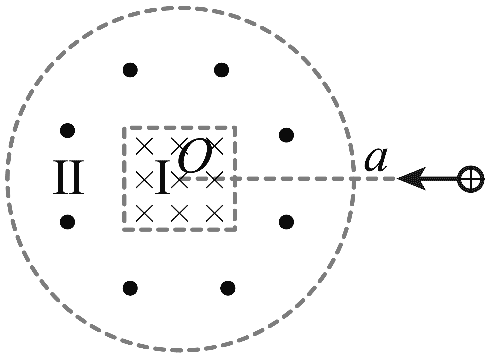．如图所示，Ⅰ 区有垂直于纸面向里的匀强磁场，其边界为正方形；Ⅱ 区有垂直于纸面向外的匀强磁场，其外边界为圆形，内边界与 I 区边界重合；正方形与圆形中心同为 O 点。I 区和 Ⅱ 区的磁感应强度大小比值为 4∶1。一带正电的粒子从 Ⅱ 区外边界上 a 点沿正方形某一条边的中垂线方向进入磁场，一段时间后从 a 点离开。取 sin37° = 0.6。则带电粒子（     ）

A．在 I 区的轨迹圆心不在 O 点

B．在 I 区和 Ⅱ 区的轨迹半径之上比为 1∶2

C．在 I 区和 Ⅱ 区的轨迹长度之比为 127∶37

D．在 I 区和 Ⅱ 区的运动时间之上比为 127∶148

【答案】

AD

 

11．某学习小组利用生活中常见物品开展“探究弹簧弹力与形变量的关系”实验。已知水的密度为 1.0×10³ kg/m³，当地重力加速度为 9.8 m/s²。实验过程如下：

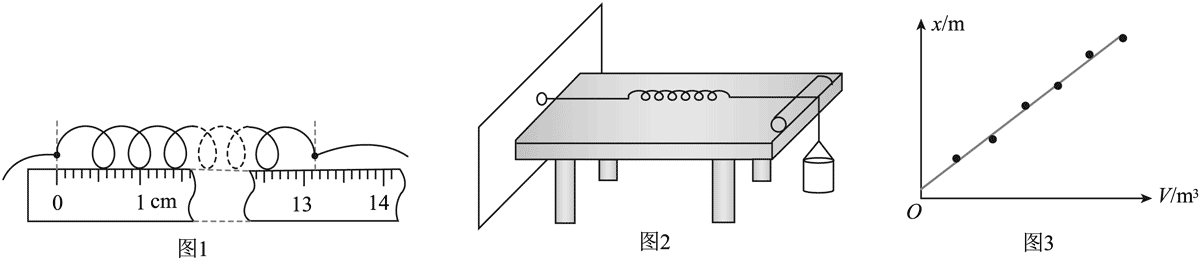
（1）将两根细绳分别系在弹簧两端，将其平放在较光滑的水平桌面上，让其中一个系绳点与刻度尺零刻度线对齐，另一个系绳点对应的刻度如图1所示，可得弹簧原长为________cm。

（2）将弹簧一端细绳系到墙上挂钩，另一端细绳跨过固定在桌面边缘的光滑金属杆后，系一个空的小桶。使弹簧和桌面上方的细绳均与桌面平行，如图 2 所示。

（3）用带有刻度的杯子量取 50 mL 水，缓慢加到小桶里，待弹簧稳定后，测量两系绳点之间的弹簧长度并记录数据。按此步骤操作 6 次。

（4）以小桶中水的体积 V 为横坐标，弹簧伸长量 x 为纵坐标，根据实验数据拟合成如图 3 所示直线，其斜率为 200 m⁻²。由此可得该弹簧的劲度系数为________N/m（结果保留 2 位有效数字）。

（5）图 3 中直线的截距为 0.0056 m，可得所用小桶质量为________kg（结果保留 2 位有效数字）。

【答案】

（1）13.14

（4）49

（5）0.028

 

12．某学生实验小组要测量一段合金丝的电阻率。所用实验器材有：

待测合金丝样品（长度约 1 m）

螺旋测微器

学生电源 E（电动势 0.4 V，内阻未知）

米尺（量程 0 ~ 100 cm）

滑动变阻器（最大阻值 20 Ω）

电阻箱（阻值范围 0 ~ 999.9 Ω）

电流表（量程 0 ~ 30 mA，内阻较小）

开关 S₁、S₂

导线若干

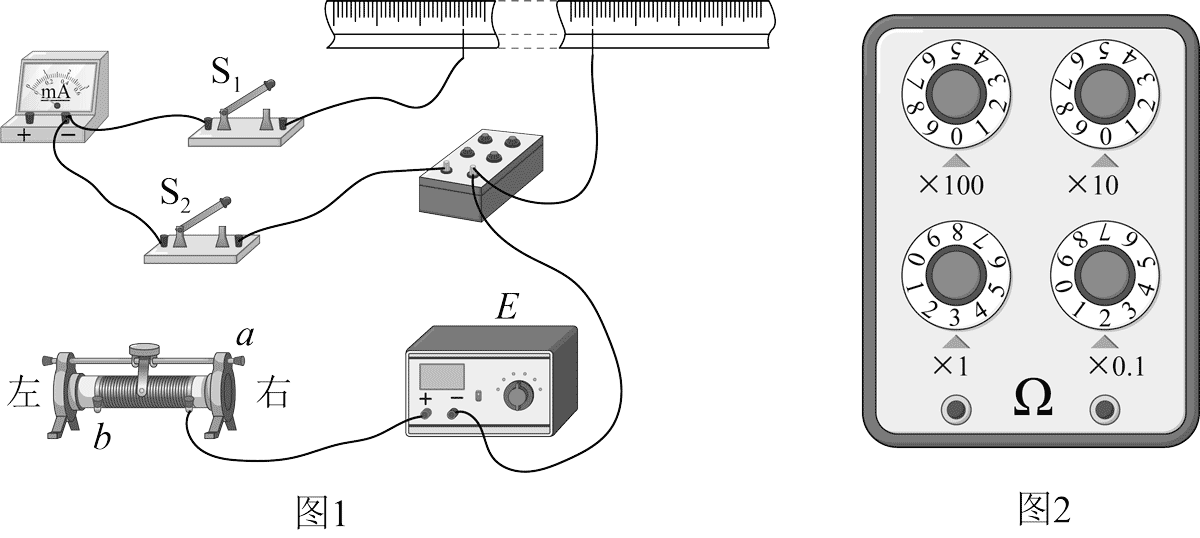
（1）将待测合金丝样品绷直固定于米尺上，将金属夹分别夹在样品 20.00 cm 和 70.00 cm 位置，用螺旋测微器测量两金属夹之间样品三个不同位置的横截面直径，读数分别为 0.499 mm、0.498 mm 和 0.503 mm，则该样品横截面直径的平均值为________mm。

（2）该小组采用限流电路，则图 1 中电流表的“+”接线柱应与滑动变阻器的接线柱________（选填“a”或“b”）相连。闭合开关前，滑动变阻器滑片应置于________端（选填“左”或“右”）。

（3）断开 S₂、闭合 S₁，调节滑动变阻器使电流表指针恰好指到 15.0 mA 刻度处。断开 S₁、闭合 S₂，保持滑动变阻器滑片位置不变，旋转电阻箱旋钮，使电流表指针仍指到 15.0 mA 处，此时电阻箱面板知图2所示，则该合金丝的电阻率为_________Ω·m（取 π = 3.14，结果保留 2 位有效数字）。

（4）为减小实验误差，可采用的做法有________（有多个正确选项）。

A．换用内阻更小的电源

B．换用内阻更小的电流表

C．换用阻值范围为 0 ~ 99.99 Ω 的电阻箱

D．多次测量该合金丝不同区间等长度样品的电阻率，再求平均值

【答案】

（1）0.500

（2）a，左

（3）1.3×10⁻⁶

（4）CD

 

13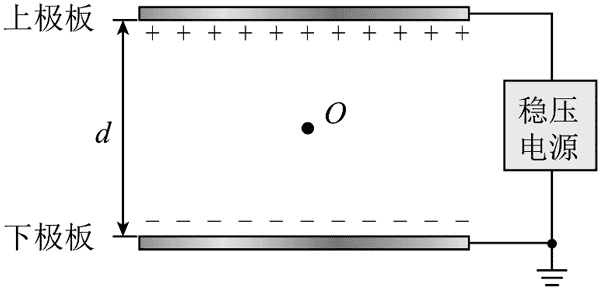．如图所示，真空中固定放置两块较大的平行金属板，板间距为 d，下极板接地，板间匀强电场大小恒为 E。现有一质量为 m、电荷量为 q（q > 0）的金属微粒，从两极板中央 O 点由静止释放。若微粒与极板碰撞前后瞬间机械能不变，碰撞后电性与极板相同，所带电荷量的绝对值不变。不计微粒重力。求：

（1）微粒第一次到达下极板所需时间；

（2）微粒第一次从上极板回到 O 点时的动量大小。

【答案】

（1）\(\sqrt {\frac{{md}}{{qE}}} \)

（2）2\(\sqrt {qEmd} \)

 

14．如图所示，长度均为 s 的两根光滑金属直导轨 MN 和 PQ 固定在水平绝缘桌面上，两者平行且相距 l，M、P 连线垂直于导轨，定滑轮位于 N、Q 连线中点正上方 h 处。MN 和 PQ 单位长度的电阻均为 r，M、P 间连接一阻值为 2sr 的电阻。空间有垂直于桌面向下的匀强磁场，磁感应强度大小为 B。过定滑轮的不可伸长绝缘轻绳拉动质量为 m、电阻不计的金属杆沿导轨向右做匀速直线运动，速度大小为 v。零时刻，金属杆位于 M、P 连线处。金属杆在导轨上时与导轨始终垂直且接触良好，重力加速度大小为 g。

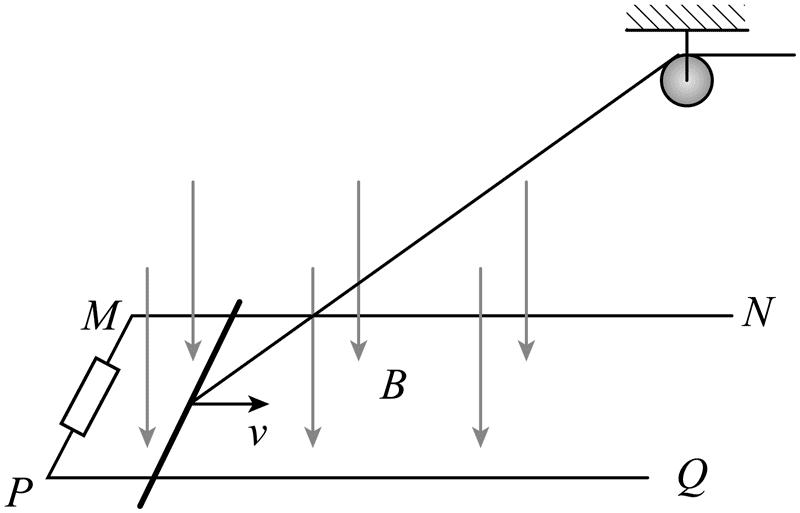
（1）金属杆在导轨上运动时，回路的感应电动势；

（2）金属杆在导轨上与 M、P 连线相距 d 时，回路的热功率；

（3）金属杆在导轨上保持速度大小 v 做匀速直线运动的最大路程。

【答案】

（1）Blv

（2）\(\frac{{{B^2}{l^2}{v^2}}}{{2r(d + s)}}\)

（3）\(\sqrt {{s^2} - \frac{{{B^2}{l^2}hv}}{{2mgr}}} \)

 

15．如图所示，倾角为 θ 的斜面固定于水平地面，斜面上固定有半径为 R 的半圆挡板和长为 7R 的直挡板。a 为直挡板下端点，bd 为半圆挡板直径且沿水平方向，c 为半圆挡板最高点，两挡板相切于 b 点，de 与 ab 平行且等长。小球乙被锁定在 c 点。小球甲从 a 点以一定初速度出发，沿挡板运动到 c 点与小球乙发生完全弹性碰撞，碰撞前瞬间解除对小球乙的锁定，小球乙在此后的运动过程中无其他碰撞。小球甲质量为 m₁，两小球均可视为质点，不计一切摩擦，重力加速度大小为 g。

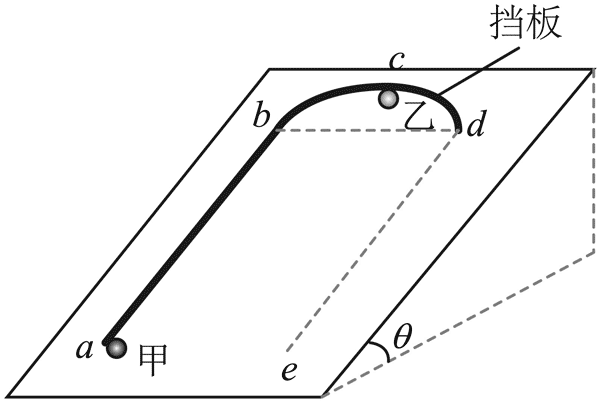
（1）求小球甲从 a 点沿直线运动到 b 点过程中的加速度大小；

（2）若小球甲恰能到达 c 点，且碰撞后小球乙能运动到 e 点，求小球乙与小球甲的质量比值应满足的条件；

（3）在满足（2）中质量比值的条件下，若碰撞后小球乙能穿过线段 de，求小球甲初动能应满足的条件。

【答案】

（1）gsinθ

（2）\(\frac{{{m_1}}}{{{m_2}}}\) ≥ 1 或 \(\frac{{{m_1}}}{{{m_2}}}\) = \(\frac{1}{7}\)

（3）\(\frac{{17}}{2}\)m₁gRsinθ < E_k0 < 12m₁gRsinθ