1．关于原子核衰变，下列说法正确的是（    ）

A．原子核衰变后生成新核并释放能量，新核总质量等于原核质量

B．大量某放射性元素的原子核有半数发生衰变所需时间，为该元素的半衰期

C．放射性元素的半衰期随环境温度升高而变长

D．采用化学方法可以有效改变放射性元素的半衰期

【答案】

B

【解析】

A．原子核衰变时释放能量，根据质能方程，总质量会减少，新核总质量小于原核质量，故 A 错误；

B．半衰期定义为大量放射性原子核半数发生衰变所需的时间，题干中强调“大量”，符合定义，故 B 正确；

C．半衰期由原子核内部结构决定，与温度无关，故 C 错误；

D．半衰期不受化学方法影响，因化学变化不改变原子核性质，故 D 错误。

故选 B。

 

2．如图，物块以某一初速度滑上足够长的固定光滑斜面，物块的水平位移、竖直位移、水平速度、竖直速度分别用 x、y、v_x、v_y 表示。物块向上运动过程中，下列图像可能正确的是（    ）

【答案】

C

 

3．如图，ABC 为半圆柱体透明介质的横截面，AC 为直径，B 为 ABC 的中点。真空中一束单色光从 AC 边射入介质，入射点为 A 点，折射光直接由 B 点出射。不考虑光的多次反射，下列说法正确的是（    ）

A．入射角 θ 小于 45°

B．该介质折射率大于 \(\sqrt 2 \)

C．增大入射角，该单色光在 BC 上可能发生全反射

D．减小入射角，该单色光在 AB 上可能发生全反射

【答案】

D

 

4．我国研制的“天问二号”探测器，任务是对伴地小行星及彗星交会等进行多目标探测。某同学提出探究方案，通过释放卫星绕小行星进行圆周运动，可测得小行星半径 R 和质量 M。为探测某自转周期为 T₀ 的小行星，卫星先在其同步轨道上运行，测得距离小行星表面高度为 h，接下来变轨到小行星表面附近绕其做匀速圆周运动，测得周期为 T₁。已知引力常量为 G，不考虑其他天体对卫星的引力，可根据以上物理得到 R = \(\frac{{{a^{\frac{2}{3}}}}}{{{b^{\frac{2}{3}}} - {a^{\frac{2}{3}}}}}\)h，M = \(\frac{{4{\pi ^2}{R^3}}}{{G{c^2}}}\)。下列选项正确的是（    ）

A．a 为 T₁，b 为 T₀，c 为 T₁                       B．a 为 T₁，b 为 T₀，c 为 T₀

C．a 为 T₀，b 为 T₁，c为 T₁                       D．a 为 T₀，b 为 T₁，c 为 T₀

【答案】

A

 

5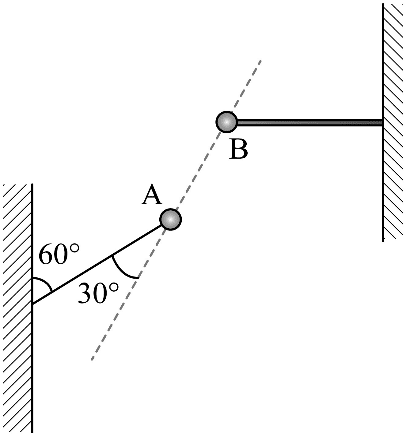．如图，两带电小球的质量均为 m，小球 A 用一端固定在墙上的绝缘轻绳连接，小球 B 用固定的绝缘轻杆连接。A 球静止时，轻绳与竖直方向的夹角为 60°，两球连线与轻绳的夹角为 30°，整个系统在同一竖直平面内，重力加速度大小为 g。下列说法正确的是（    ）

A．A 球静止时，轻绳上拉力为 2mg

B．A 球静止时，A 球与 B 球间的库仑力为 2mg

C．若将轻绳剪断，则剪断瞬间 A 球加速度大小为 g

D．若将轻绳剪断，则剪断瞬间轻杆对 B 球的作用力变小

【答案】

C

【解析】

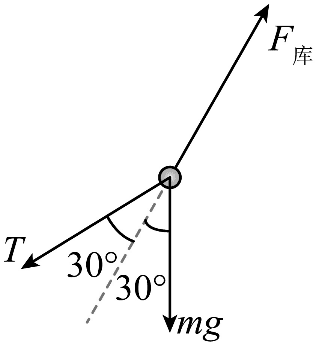AB．根据题意 A 球静止时，对 A 球受力分析，如图所示

由平行四边形定则及几何关系，轻绳上拉力为 T = mg

A 球与 B 球间的库仑力 F = 2mgcos30° = \(\sqrt 3 \)mg

故 AB 错误；

C．若将轻绳剪断，则剪断瞬间A球受到轻绳的拉力消失，其它两力保持不变，根据三力平衡知识，此时A球的合外力大小为 mg，则加速度大小为 g，故 C 正确；

D．若将轻绳剪断，则剪断瞬间 B 球受到的库仑力、重力不变，小球仍然处在静止状态，则轻杆对 B 球的作用力不变，故 D 错误。

故选 C。

 

6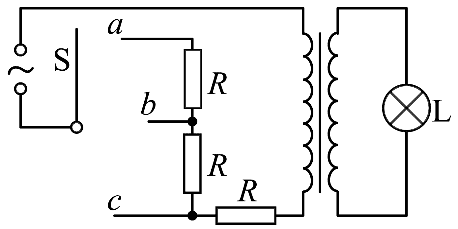．如图，某小组设计了灯泡亮度可调的电路，a、b、c 为固定的三个触点，理想变压器原、副线圈匝数比为 k，灯泡 L 和三个电阻的阻值均恒为 R，交变电源输出电压的有效值恒为 U。开关 S 与不同触点相连，下列说法正确的是（    ）

A．S 与 a 相连，灯泡的电功率最大

B．S 与 a 相连，灯泡两端的电压为 \(\frac{{kU}}{{{k^2} + 3}}\)

C．S 与 b 相连，流过灯泡的电流为 \(\frac{U}{{({k^2} + 2)R}}\)

D．S 与 c 相连，灯泡的电功率为 \(\frac{{{U^2}}}{{({k^2} + 1)R}}\)

【答案】

B

 

7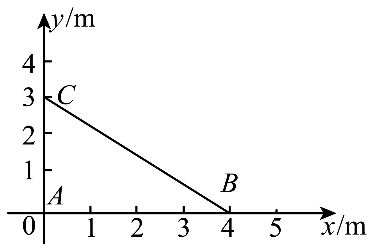．如图，A（0,0）、B（4,0）、C（0,3）在 xy 平面内，两波源分别置于 A、B 两点。t = 0 时，两波源从平衡位置起振，起振方向相同且垂直于 xy 平面。频率均为 2.5 Hz。两波源持续产生振幅相同的简谐横波，波分别沿 AC、BC 方向传播，波速均为 10 m/s。下列说法正确的是（    ）

A．两横波的波长均为 4 m

B．t = 0.4 s 时，C 处质点加速度为 0

C．t = 0.4 s 时，C 处质点速度不为 0

D．t = 0.6 s 时，C 处质点速度为 0

【答案】

AD

 

8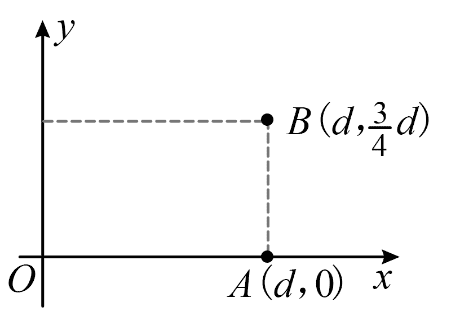．一匀强电场的方向平行于 xOy 平面，平面内 A 点和 B 点的位置如图所示。电荷量为 + q、− q 和 + 2q 的三个试探电荷先后分别置于 O 点、A 点和 B 点时，电势能均为 E_p（E_p > 0）。下列说法正确的是（    ）

A．OA 中点的电势为零

B．电场的方向与 x 轴正方向成 60° 角

C．电场强度的大小为 \(\frac{{\sqrt 2 {E_{\rm{p}}}}}{{qd}}\)

D．电场强度的大小为 \(\frac{{2\sqrt 2 {E_{\rm{p}}}}}{{qd}}\)

【答案】

AD

【解析】

A．根据题意可知 O 点、A 点和 B 点的电势分别为 φ_O = \(\frac{{{E_{\rm{p}}}}}{q}\)，φ_A = − \(\frac{{{E_{\rm{p}}}}}{q}\)，φ_B = \(\frac{{{E_{\rm{p}}}}}{2q}\)。故 OA 中点的电势为 φ_M = \(\frac{1}{2}\)(φ_O + φ_A) = 0。

故 A 正确；

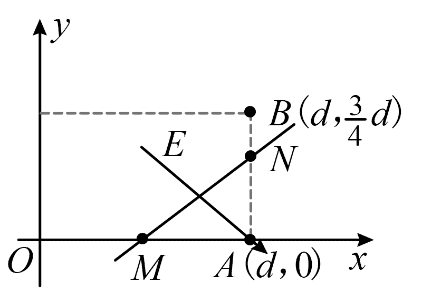B．如图，设 N 点为 AB 的三等分点，同理易知 N 点电势为 0，连接 MN 为一条等势线，过 A 点做 MN 的垂线，可知电场线沿该垂线方向，指向右下方，由 AM = AN 可知 ∠NMA = 45°，故电场的方向与 x 轴正方向成 45° 角，故 B 错误；

CD．电场强度的大小为

E = \(\frac{{0 - ( - \frac{{{E_{\rm{p}}}}}{q})}}{{\frac{1}{2}d\cos 45^\circ }}\) = \(\frac{{2\sqrt 2 {E_{\rm{p}}}}}{{qd}}\)

故 C 错误，D 正确。

故选 AD。

 

9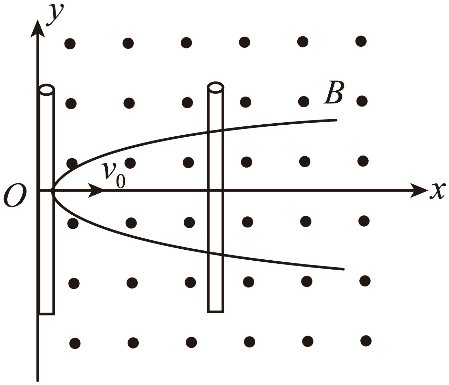．如图，关于 x 轴对称的光滑导轨固定在水平面内，导轨形状为抛物线，顶点位于 O 点。一足够长的金属杆初始位置与 y 轴重合，金属杆的质量为 m，单位长度的电阻为 r₀。整个空间存在竖直向上的匀强磁场，磁感应强度为 B。现给金属杆一沿 x 轴正方向的初速度 v₀，金属杆运动过程中始终与 y 轴平行，且与电阻不计的导轨接触良好。下列说法正确的是（    ）

A．金属杆沿 x 轴正方向运动过程中，金属杆中电流沿 y 轴负方向

B．金属杆可以在沿 x 轴正方向的恒力作用下做匀速直线运动

C．金属杆停止运动时，与导轨围成的面积为 \(\frac{{m{v_0}{r_0}}}{{{B^2}}}\)

D．若金属杆的初速度减半，则金属杆停止运动时经过的距离小于原来的一半

【答案】

AC

 

10．如图，某爆炸能量测量装置由装载台和滑轨等构成，C 是可以在滑轨上运动的标准测量件，其规格可以根据测量需求进行调整。滑轨安装在高度为 h 的水平面上。测量时，将弹药放入装载台圆筒内，两端用物块 A 和 B 封装，装载台与滑轨等高。引爆后，假设弹药释放的能量完全转化为 A 和 B 的动能。极短时间内 B 嵌入 C 中形成组合体 D，D 与滑轨间的动摩擦因数为 μ。D 在滑轨上运动 s₁ 距离后抛出，落地点距抛出点水平距离为 s₂，根据 s₂ 可计算出弹药释放的能量。某次测量中，A、B、C 质量分别为 3m、m、5m，s₁ = \(\frac{h}{\mu }\)，整个过程发生在同一竖直平面内，不计空气阻力，重力加速度大小为 g。则（    ）

A．D 的初动能与爆炸后瞬间 A 的动能相等

B．D 的初动能与其落地时的动能相等

C．弹药释放的能量为 36mgh（1 + \(\frac{{s_2^2}}{{4{h^2}}}\)）

D．弹药释放的能量为 48mgh（1 + \(\frac{{s_2^2}}{{4{h^2}}}\)）

【答案】

BD

 

11．某同学通过观察小球在黏性液体中的运动，探究其动力学规律，步骤如下：

  

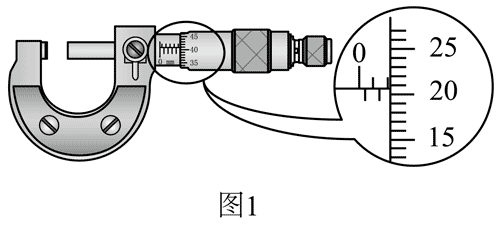
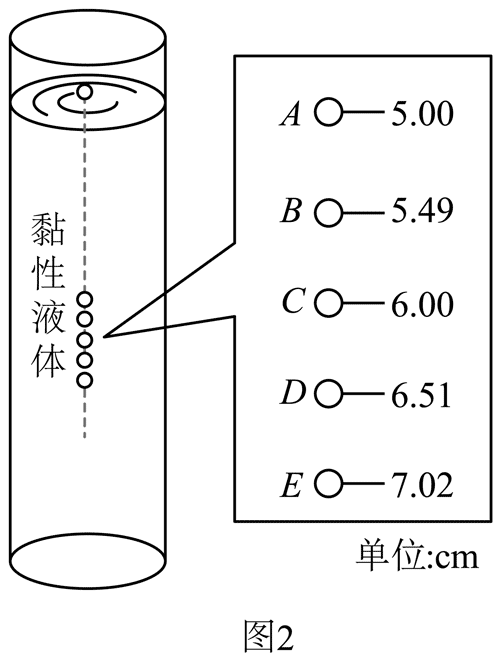
（1）用螺旋测微器测量小球直径 D 如图 1 所示，D =__________mm。

（2）在液面处由静止释放小球，同时使用频闪摄影仪记录小球下落过程中不同时刻的位置，频闪仪每隔 0.5 s 闪光一次。装置及所拍照片示意图如图 2 所示（图中的数字是小球到液面的测量距离，单位是 cm）。

（3）根据照片分析，小球在 A、E 两点间近似做匀速运动，速度大小 v =__________m/s（保留 2 位有效数字）。

（4）小球在液体中运动时受到液体的黏滞阻力 f = kDv（k 为与液体有关的常量），已知小球密度为 ρ，液体密度为 ρ₀，重力加速度大小为 g，则 k 的表达式为 k =__________（用题中给出的物理量表示）。

（5）为了进一步探究动力学规律，换成直径更小的同种材质小球，进行上述实验，匀速运动时的速度将__________（填“增大”“减小”或“不变”）。

【答案】

（1）2.207

（3）0.010

（4）\(\frac{{(\rho  - {\rho _0})g\pi {D^2}}}{{6v}}\)

（5）减小

 

12．车辆运输中若存在超载现象，将带来安全隐患。由普通水泥和导电材料混合制成的导电水泥，可以用于监测道路超载问题。某小组对此进行探究。

（1）选择一块均匀的长方体导电水泥块样品，用多用电表粗测其电阻。将多用电表选择开关旋转到“×1 k”挡，正确操作后，指针位置如图 1 所示，则读数为__________Ω。

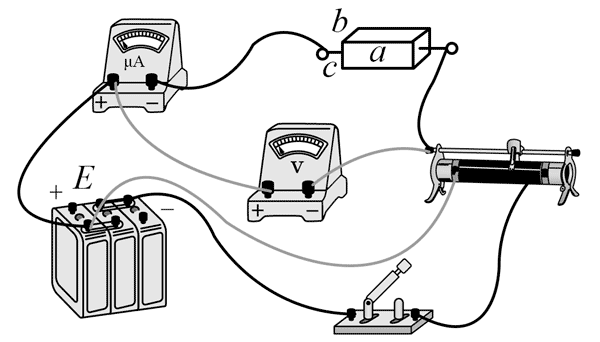
（2）进一步提高实验精度，使用伏安法测量水泥块电阻，电源 E 电动势 6 V，内阻可忽略，电压表量程 0 ~ 6 V，内阻约 10 kΩ，电流表程 0 ~ 600 μA，内阻约 100 Ω。实验中要求滑动变阻器采用分压接法，在图 2 中完成余下导线的连接__________。

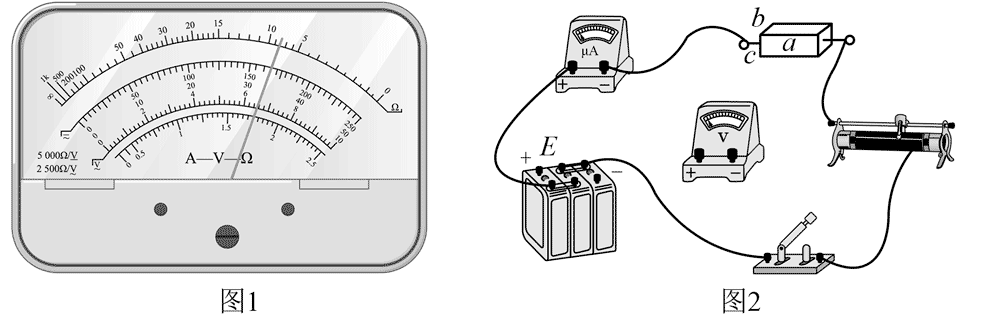
（3）如图 2，测量水泥块的长为 a，宽为 b，高为 c。用伏安法测得水泥块电阻为 R，则电阻率 ρ =__________（用 R、a、b、c 表示）。

（4）测得不同压力 F 下的电阻 R，算出对应的电阻率 ρ，作出 ρ–F 图像如图 3 所示。

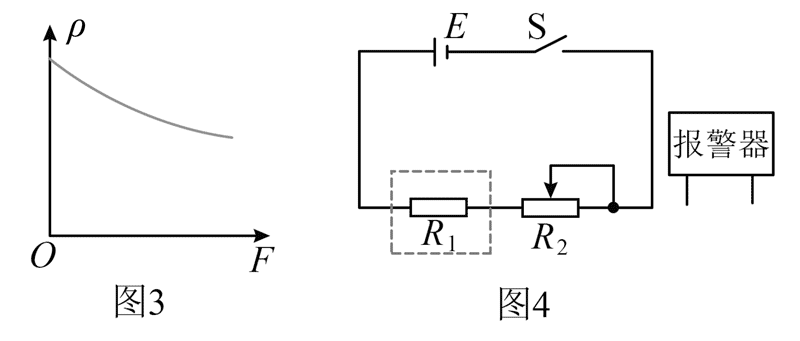
（5）基于以上结论，设计压力报警系统，电路如图 4 所示。报警器在两端电压大于或等于 3 V 时启动，R₁ 为水泥块，R₂ 为滑动变阻器，当 R₂ 的滑片处于某位置，R₁ 上压力大于或等于 F₀ 时，报警器启动。报警器应并联在__________两端（填“R₁”或“R₂”）。

（6）若电源 E 使用时间过长，电动势变小，R₁ 上压力大于或等于 F₁ 时，报警器启动，则 F₁__________F₀（填“大于”“小于”或“等于”）。

【答案】

（1）8000

（2）如图（采用电流表内接法）

（3）\(\frac{{Rab}}{c}\)

（5）R₂

（6）大于

 

13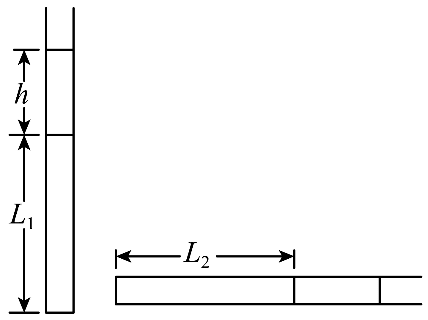．用热力学方法可测量重力加速度。如图所示，粗细均匀的细管开口向上竖直放置，管内用液柱封闭了一段长度为 L₁ 的空气柱。液柱长为 h，密度为 ρ。缓慢旋转细管至水平，封闭空气柱长度为 L₂，大气压强为 p₀。

（1）若整个过程中温度不变，求重力加速度 g 的大小；

（2）考虑到实验测量中存在各类误差，需要在不同实验参数下进行多次测量，如不同的液柱长度、空气柱长度、温度等。某次实验测量数据如下，液柱长 h = 0.20 m，细管开口向上竖直放置时空气柱温度 T₁ = 305.7 K。水平放置时调控空气柱温度，当空气柱温度 T₂ = 300.0 K 时，空气柱长度与竖直放置时相同。已知 ρ = 1.0×10³ kg/m³，p₀ = 1.0×10⁵ Pa。根据该组实验数据，求重力加速度 g 的值。

【答案】

（1）g = \(\frac{{{p_0}({L_2} - L)}}{{\rho h{L_1}}}\)

（2）g = 9.5 m/s²

 

14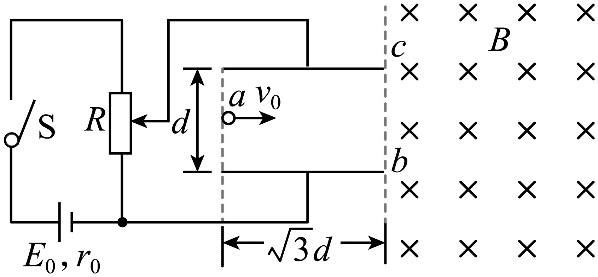．如图。直流电源的电动势为 E₀，内阻为 r₀，滑动变阻器 R 的最大阻值为 2r₀，平行板电容器两极板水平放置，板间距离为 d，板长为 \(\sqrt 3 \)d，平行板电容器的右侧存在方向垂直纸面向里的匀强磁场。闭合开关 S，当滑片处于滑动变阻器中点时，质量为 m 的带正电粒子以初速度 v₀ 水平向右从电容器左侧中点 a 进入电容器，恰好从电容器下极板右侧边缘 b 点进入磁场，随后又从电容器上极板右侧边缘 c 点进入电容器，忽略粒子重力和空气阻力。

（1）求粒子所带电荷量 q；

（2）求磁感应强度 B 的大小；

（3）若粒子离开 b 点时，在平行板电容器的右侧再加一个方向水平向右的匀强电场，场强大小为 \(\frac{{4\sqrt 3 {E_0}}}{{3d}}\)，求粒子相对于电容器右侧的最远水平距离 x_m。

【答案】

（1）q = \(\frac{{mv_0^2}}{{{E_0}}}\)

（2）B = \(\frac{{2{E_0}}}{{d{v_0}}}\)

（3）\(\frac{{2 + \sqrt 3 }}{2}\)d

 

15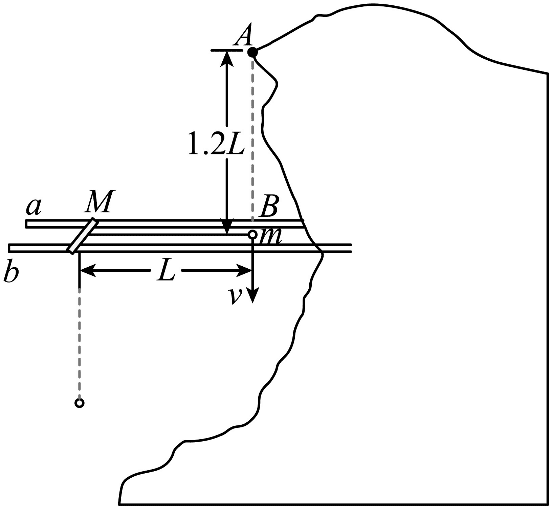．某地为发展旅游经济，因地制宜利用山体举办了机器人杂技表演。表演中，需要将质量为 m 的机器人抛至悬崖上的 A 点，图为山体截面与表演装置示意图。a、b 为同一水平面上两条光滑平行轨道，轨道中有质量为 M 的滑杆。滑杆用长度为 L 的轻绳与机器人相连。初始时刻，轻绳绷紧且与轨道平行，机器人从 B 点以初速度 v 竖直向下运动，B 点位于轨道平面上，且在 A 点正下方，AB = 1.2L。滑杆始终与轨道垂直，机器人可视为质点且始终作同一竖直平面内运动，不计空气阻力，轻绳不可伸长，sin37° = 0.6，重力加速度大小为 g。

（1）若滑杆固定，v = \(\sqrt {gl} \)，当机器人运动到滑杆正下方时，求轻绳拉力的大小；

（2）若滑杆固定，当机器人运动到滑杆左上方且轻绳与水平方向夹角为 37° 时，机器人松开轻绳后被抛至 A 点，求 v 的大小；

（3）若滑杆能沿轨道自由滑动，M = km，且 k ≥ 1，当机器人运动到滑杆左上方且轻绳与水平方向夹角为 37° 时，机器人松开轻绳后被抛至 A 点，求 v 与 k 的关系式及 v 的最小值。

【答案】

（1）F = 4mg

（2）v = \(\sqrt {\frac{{37}}{{10}}gl} \)

（3）v = \(\sqrt {\frac{{9kgl}}{{10(k + 1)}} + \frac{{14}}{5}gl} \)，v_min = \(\sqrt {\frac{{13}}{4}gl} \)