1．已知金属铷、钾、钠、钙的逸出功分别为 2.13 eV、2.25eV、2.29 eV、3.20 eV，用光子能量为 2.20 eV 的单色光照射这些金属的表面，能逸出光电子的金属是（    ）

A．铷             B．钾             C．钠             D．钙

【答案】

A

 

2．某变压器输入正弦交流电的电压有效值为 220 V，输出电压最大值为 11\(\sqrt 2 \) V，该变压器视为理想变压器，其原、副线圈匝数之比为（    ）

A．20∶\(\sqrt 2 \)          B．20\(\sqrt 2 \)∶1        C．20∶1               D．1∶20

【答案】

C

 

3．某乘客乘坐的动车进站时，动车速度从 36 km/h 减小为 0，此过程可视为匀减速直线运动，期间该乘客的脉搏跳动了 70 次。已知他的脉搏跳动每分钟约为 60 次，则此过程动车行驶距离约为（    ）

A．216 m               B．350 m               C．600 m               D．700 m

【答案】

B

 

4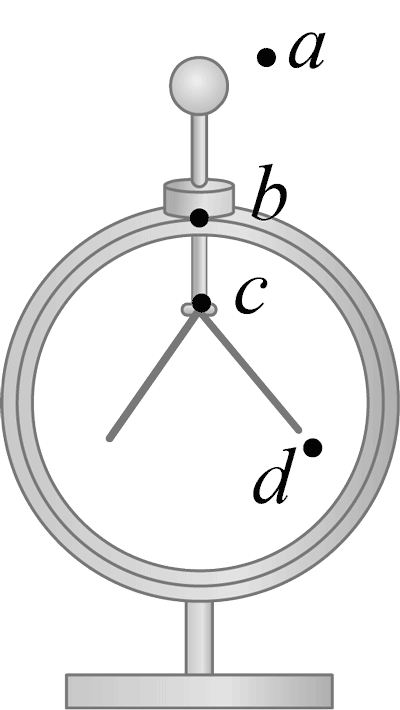．用带电玻璃棒接触验电器的金属球，移走玻璃棒，验电器内的两片金属箔张开，稳定后如图。图中 a、b、c、d 四点电场强度最强的是（    ）

A．a 点           B．b 点          C．c 点           D．d 点

【答案】

D

【解析】

bc 两点分别在金属外壳内部和金属杆的内部，则两点的场强均为零；在金属箔上的最下端电荷分布比金属球上更密集，且d点距离金箔的下端较近，可知 d 点的场强比 a 点大，则电场强度最大的点在 d 点。

故选 D。

 

5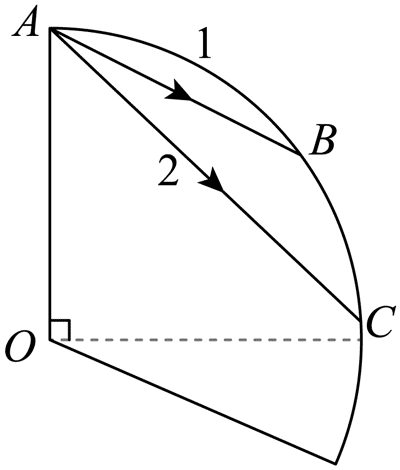．如图扇形的材料，折射率大于 \(\sqrt 2 \)，现有两条光线 1 和 2，从扇形材料的A点传播，光线 1 传到圆弧（\(\frac{1}{4}\) 圆）AC 的中点 B，光线 2 传播到 C 点偏上，则两光线发生下列哪种情况（    ）

A．1 不全反射，2 全反射           B．都不全反射

C．都全反射                                  D．1 全反射，2 不全反射

【答案】

C

 

6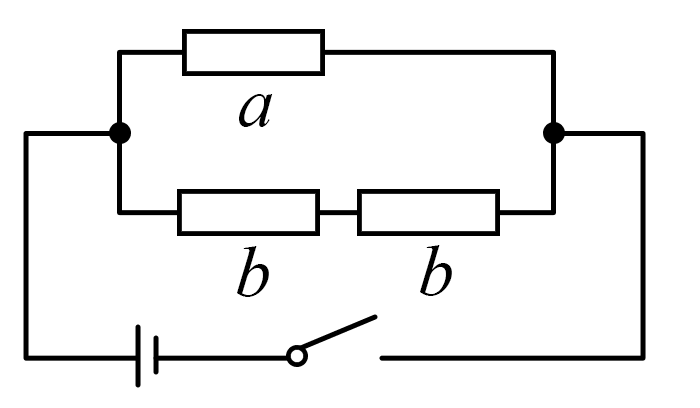．如图电路中，材质相同的金属导体 a 和 b，横截面积分别为 S₁、S₂，长度分别为 l₁、l₂。闭合开关后，a 和 b 中自由电子定向移动的平均速率之比为（    ）

A．l₁∶2l₂                      B．2l₂∶l₁

C．l₂S₁∶2l₁S₂                D．2l₂S₂∶l₁S₁

【答案】

B

 

7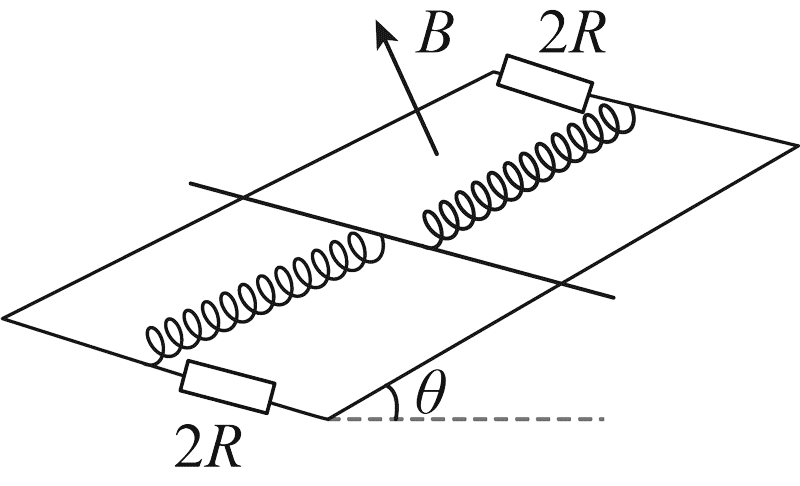．如图，两条固定的光滑平行金属导轨，所在平面与水平面夹角为 θ，间距为 l，导轨电阻忽略不计，两端各接一个阻值为 2R 的定值电阻，形成闭合回路：质量为 m 的金属棒垂直导轨放置，并与导轨接触良好，接入导轨之间的电阻为 R；劲度系数为 k 的两个完全相同的绝缘轻质弹簧与导轨平行，一端固定，另一端均与金属棒中间位置相连，弹簧的弹性势能 E_p 与形变量 x 的关系为 E_p = \(\frac{1}{2}\)kx²；将金属棒移至导轨中间位置时，两弹簧刚好处于原长状态；整个装置处于垂直导轨所在平面向上的匀强磁场中，磁感应强度大小为 B。将金属棒从导轨中间位置向上移动距离 a 后静止释放，金属棒沿导轨向下运动到最远处，用时为 t，最远处与导轨中间位置距离为 b，弹簧形变始终在弹性限度内。此过程中（    ）

A．金属棒所受安培力冲量大小为 \(\frac{{{B^2}{l^2}(a + b)}}{R}\)

B．每个弹簧对金属棒施加的冲量大小为 \(\frac{{{B^2}{l^2}(a + b)}}{{4R}}\) + \(\frac{{mgt\sin \theta }}{2}\)

C．每个定值电阻产生的热量为 \(\frac{{k({a^2} - {b^2})}}{8}\) + \(\frac{{mg(a + b)\sin \theta }}{4}\)

D．金属棒的平均输出功率为 \(\frac{{k({a^2} - {b^2}) + mg(a + b)\sin \theta }}{{2t}}\)

【答案】

D

 

8．在“用油膜法估测油酸分子的大小”实验中（    ）

A．估测油酸分子大小时，油酸分子可以视为球形

B．油膜的形状稳定后，油酸分子仍然在做热运动

C．计算油膜面积时，忽略所有不完整的小正方形

D．与油酸酒精溶液相比，纯油酸更容易在水面形成单分子油膜

【答案】

AB

【解析】

A．在油膜法测分子直径的实验中，把油膜看成单分子油膜，且分子紧密排列。由于分子形状复杂，为简化计算，通常将其视为球形模型，油膜的厚度可以近似看成是球形分子的直径，故 A 正确；

B．分子在永不停息地做无规则热运动，与宏观物体是否处于稳定状态无关。油膜稳定时，油酸分子仍然在做热运动，故 B 正确；

C．在计算油膜面积时，为了更准确地估算油膜的面积，对于周边不完整的格子，大于半格记为一个单位面积，小于半格的不计面积，而不是不完整的格子不计面积，故 C 错误；

D．酒精可以溶解油酸，使油酸更容易在水面上展开形成单分子油膜，所以实验时加酒精比不加酒精更好地展开油膜，故 D 错误。

故选 AB。

 

9．独竹漂是我国一项民间技艺。如图，在平静的湖面上，独竹漂选手手持划杆踩着楠竹，沿直线减速滑行，选手和楠竹相对静止，则（     ）

A．选手所受合力为零

B．楠竹受到选手作用力的方向一定竖直向下

C．手持划杆可使选手（含划杆）的重心下移，更易保持平衡

D．选手受到楠竹作用力的方向与选手（含划杆）的重心在同一竖直平面

【答案】

CD

【解析】

A．选手和楠竹在水里减速滑行，速度在变化，根据牛顿第二定律可知合力不为零，故 A 错误；

B．楠竹在水平方向有加速度，选手对楠竹的力在竖直方向有重力，水平方向有摩擦力，所以选手对楠竹的力方向不是竖直向下，故 B 错误；

C．选手和楠竹相对静止，且减速滑行，选手和楠竹的重心要在同一竖直面上才能保持相对稳定，故 C 正确；

D．选手和楠竹构成的整体在减速滑行，受到的合力不为零，根据力的作用线和重心的关系可知整体的重心与楠竹受到合力作用线应该在同一竖直面上，故 D 正确。

故选 CD。

 

10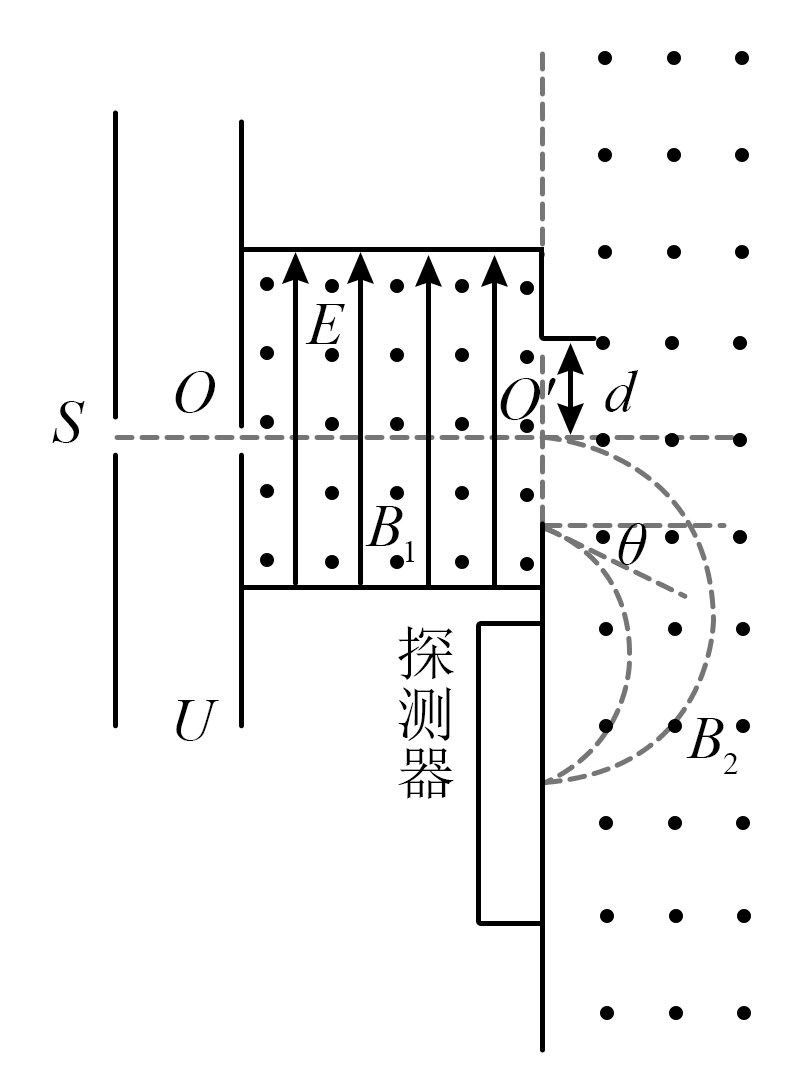．如图，带等量正电荷 q 的 M、N 两种粒子，以几乎为 0 的初速度从 S 飘入电势差为U的加速电场，经加速后从 O 点沿水平方向进入速度选择器（简称选择器）。选择器中有竖直向上的匀强电场和垂直纸面向外的匀强磁场。当选择器的电场强度大小为 E，磁感应强度大小为 B₁，右端开口宽度为 2d 时，M粒子沿轴线 OO′ 穿过选择器后，沿水平方向进入磁感应强度大小为 B₂、方向垂直纸面向外的匀强磁场（偏转磁场），并最终打在探测器上；N 粒子以与水平方向夹角为 θ 的速度从开口的下边缘进入偏转磁场，并与 M 粒子打在同一位置，忽略粒子重力和粒子间的相互作用及边界效应，则（    ）

A．M粒子质量为 \(\frac{{2qUB_1^2}}{{{E^2}}}\)

B．刚进入选择器时，N 粒子的速度小于 M 粒子的速度

C．调节选择器，使 N 粒子沿轴线 OO′ 穿过选择器，此时选择器的电场强度与磁感应强度大小之比为 \(\frac{{4EU\cos \theta }}{{4U{B_1} - Ed{B_2}}}\)

D．调节选择器，使N粒子沿轴线 OO′ 进入偏转磁场，打在探测器上的位置与调节前 M 粒子打在探测器上的位置间距为 \(\frac{{4U{B_1}}}{{E{B_2}}}\) + \(\frac{{(Ed{B_2} - 4U{B_1})\sqrt U }}{{E{B_2}\cos \theta \sqrt {U - Ed} }}\)

【答案】

AD

 

11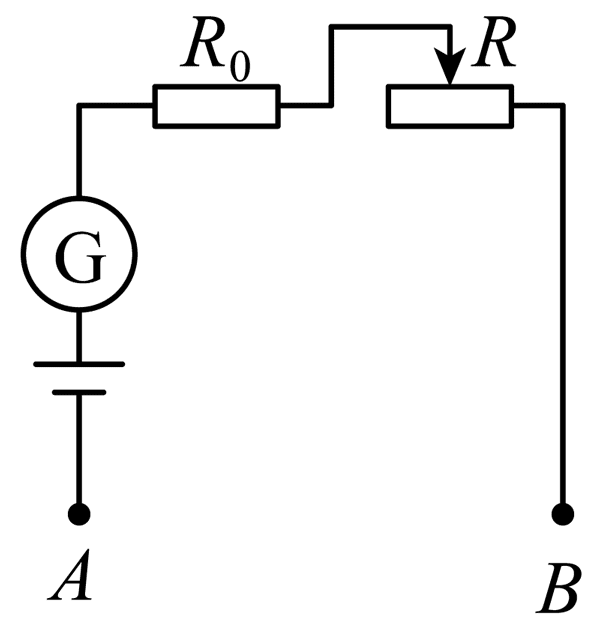．某小组将电流表改装成欧姆表，所用器材有电源（电动势 E = 1.5 V，内阻不计），电流表（满偏电流 I_g = 100 μA，内阻 R_g = 100 Ω），电阻 R₀ = 500 Ω，滑动变阻器 R（0 ~ 20 kΩ），导线若干，电路如图。

（1）欧姆调零时，应先将 A、B______，再调节滑动变阻器，使电流表示数为______μA，此时滑动变阻器的阻值为______kΩ。

（2）调零后，在 A、B 间接入电阻 R_x，当电流表示数为 60 μA 时，R_x 为______kΩ。

【答案】

（1）短接，100，14.4

（2）10

 

12．在用如图甲的装置做“探究加速度与力、质量的关系”实验中：

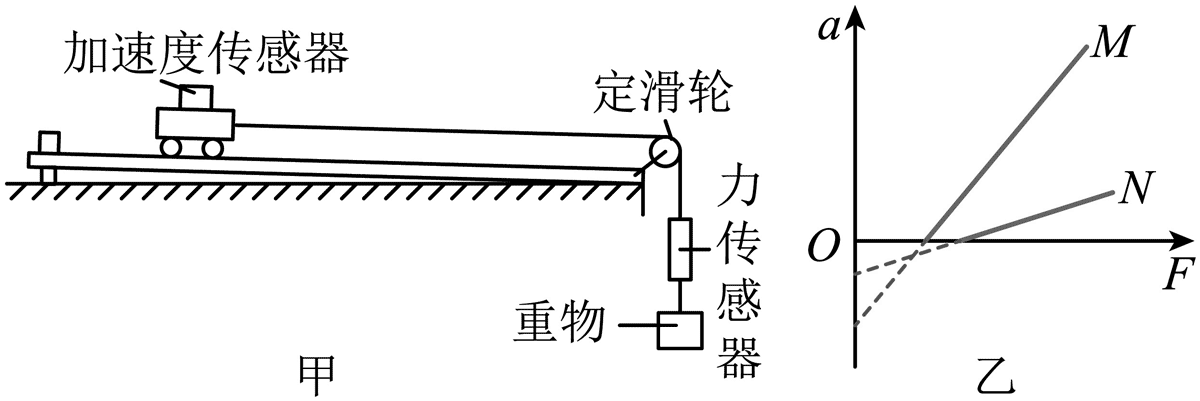
（1）探究小车加速度与小车所受拉力的关系时，需保持小车（含加速度传感器，下同）质量不变，这种实验方法是_______________。

（2）实验时，调节定滑轮高度，使连接小车的细绳与轨道平面保持_____。

（3）由该装置分别探究 M、N 两车加速度 a 和所受拉力 F 的关系，获得 a–F 图像如图乙，通过图乙分析实验是否需要补偿阻力（即平衡阻力）。如果需要，说明如何操作；如果不需要，说明理由。

（4）悬挂重物让 M、N 两车从静止释放经过相同位移的时间比为 n，两车均未到达轨道末端，则两车加速度之比 a_M∶a_N =_____。

【答案】

（1）控制变量法

（2）平行

（3）需要；撤出细绳连接的力传感器和重物，将木板左端用垫块垫起适当高度，使小车能沿木板匀速下滑。

（4）1∶n²

【解析】

（1）在探究小车加速度与小车所受拉力的关系时，需保持小车（含加速度传感器）质量不变，这种实验方法是控制变量法。

（2）实验时，为使小车受到的合外力等于细绳的拉力，要调节定滑轮高度，使连接小车的细绳与轨道平面保持平行，保证细绳对小车的拉力方向与小车运动方向一致，减小实验误差。

（3）由图乙可知，当拉力 F 为某一值时才产生加速度，说明小车受到摩擦力，需要补偿阻力。补偿方法：撤出细绳连接的力传感器和重物，将木板左端用垫块垫起适当高度，使小车能沿木板匀速下滑。

（4）两车均从静止释放，都做初速度为零的匀加速直线运动，根据匀变速直线运动的位移公式 x = \(\frac{1}{2}\)at² 可知 a = \(\frac{{2x}}{{{t^2}}}\)。因为 t_M∶t_N = n∶1，可解得 a_M∶a_N = t_N²∶t_M² = 1∶n²

 

13．某乐器发出频率为两倍关系的两个纯音（简谐声波），其波形叠加后呈现一种周期性变化。图甲和图乙分别为同一时刻两列简谐声波单独沿 x 正方向传播的波形图，图中的坐标原点位于同一质点处，声速为 340 m/s。

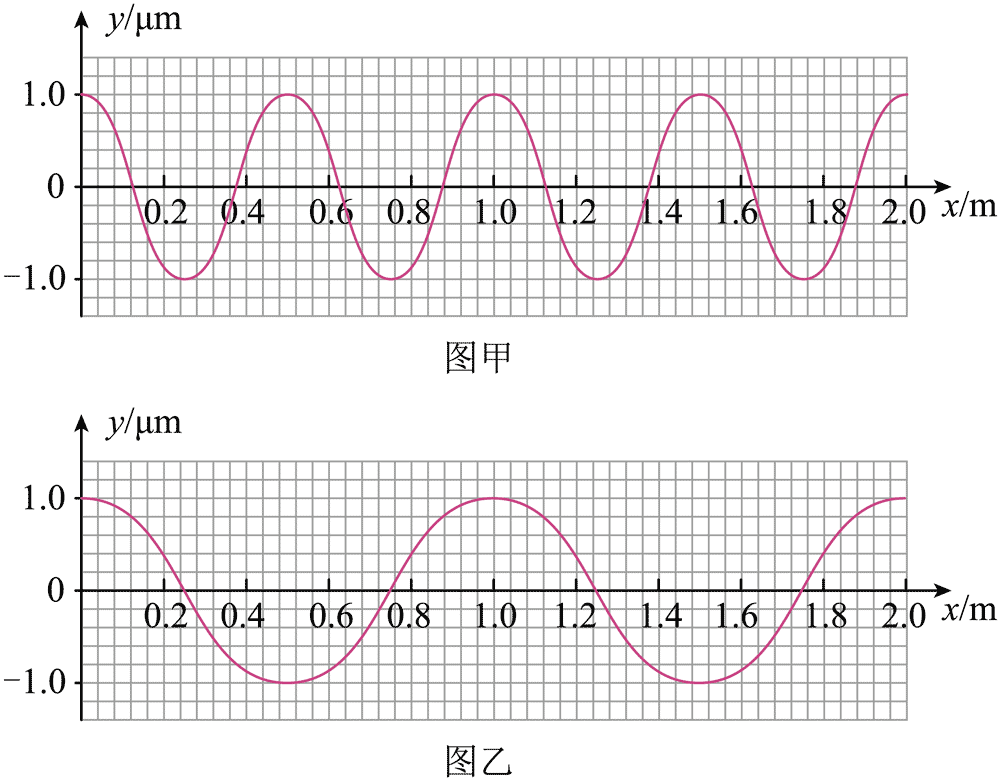
（1）从图中读出这两列波的波长。

（2）该时刻这两列波叠加，分别求 x = 0 和 x = 0.375 m 处的质点在该时刻偏离平衡位置的位移。

（3）求这两列波叠加后的周期。

【答案】

（1）λ₁ = 0.5 m，λ₂ = 1 m

（2）2 μm，− \(\frac{{\sqrt 2 }}{2}\) μm

（3）\(\frac{1}{{340}}\) s

 

14．带电粒子绕着带电量为 + Q 的源电荷做轨迹为椭圆的曲线运动，源电荷固定在椭圆左焦点 F 上，带电粒子电量为 − q；已知椭圆焦距为 c，半长轴为 a，电势计算公式为 φ = \(\frac{{kQ}}{r}\)，带电粒子速度的平方与其到电荷的距离的倒数满足如图关系。

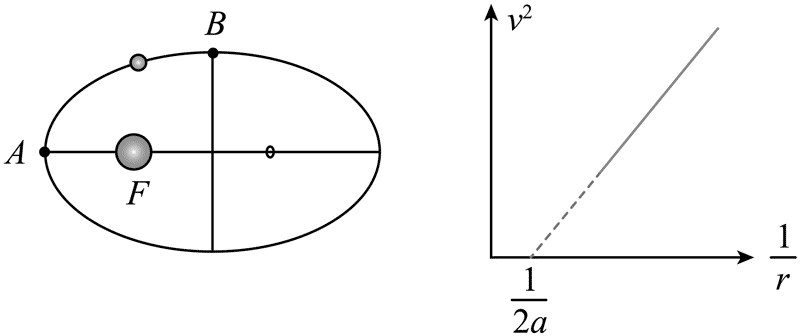
（1）求在椭圆轨道半短轴顶点 B 的电势；

（2）求带电粒子从 A 到 B 的运动过程中，电场力对带电粒子做的功；

（3）用推理论证带电粒子动能与电势能之和是否守恒；若守恒，求其动能与电势能之和；若不守恒，说明理由。

【答案】

（1）φ_B = \(\frac{{kQ}}{a}\)

（2）− kQq\(\left( {\frac{2}{{2a - c}} - \frac{1}{a}} \right)\)

（3）守恒，− \(\frac{{kQq}}{{2a}}\)

 

15．图甲为某智能分装系统工作原理示意图，每个散货经倾斜传送带由底端 A 运动到顶端 B 后水平抛出，撞击冲量式传感器使其输出一个脉冲信号，随后竖直掉入以与水平传送带共速度的货箱中，此系统利用传感器探测散货的质量，自动调节水平传送带的速度，实现按规格分装。倾斜传送带与水平地面夹角为 30°，以速度 v₀ 匀速运行。若以相同的时间间隔 Δt 将散货以几乎为 0 的速度放置在倾斜传送带底端 A，从放置某个散货时开始计数，当放置第 10 个散货时，第 1 个散货恰好被水平抛出。散货与倾斜传送带间的动摩擦因数 μ = \(\frac{{\sqrt 3 }}{2}\)，到达顶端前已与传送带共速。设散货与传感器撞击时间极短，撞击后竖直方向速度不变，水平速度变为 0。每个长度为 d 的货箱装总质量为 M 的一批散货。若货箱之间无间隔，重力加速度为 g。分装系统稳定运行后，连续装货，某段时间传感器输出的每个脉冲信号与横轴所围面积为 I 如图乙，求这段时间内：

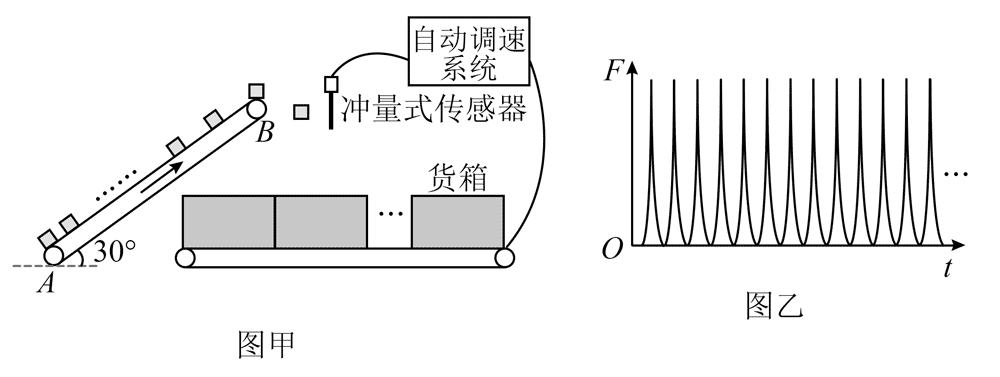
（1）单个散货的质量。

（2）水平传送带的平均传送速度大小。

（3）倾斜传送带的平均输出功率。

【答案】

（1）\(\frac{I}{{{v_0}}}\)

（2）\(\frac{{dI}}{{M{v_0}\Delta t}}\)

（3）\(\frac{{I(2{v_0} + 9g\Delta t)}}{{2\Delta t}}\)