1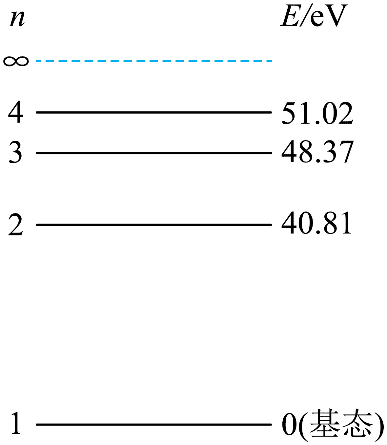．利用电子与离子的碰撞可以研究离子的能级结构和辐射特性。He⁺ 离子相对基态的能级图（设基态能量为 0）如图所示。用电子碰撞 He⁺ 离子使其从基态激发到可能的激发态，若所用电子的能量为 50 eV，则 He⁺ 离子辐射的光谱中，波长最长的谱线对应的跃迁为（    ）

A．n = 4→n = 3 能级           B．n = 4→n = 2 能级

C．n = 3→n = 2 能级            D．n = 3→n = 1 能级

【答案】

C

【解析】

根据题意可知，用能量为 50 eV 的电子碰撞 He⁺ 离子，可使 He⁺ 离子跃迁到 n = 3 能级和 n = 2 能级，由

ΔE = E_m – E_n = hν = h\(\frac{c}{\lambda }\)

可知，波长最长的谱线对应的跃迁为 n = 3→n = 2能级。

故选 C。

 

2．如图，一小星球与某恒星中心距离为 R 时，小星球的速度大小为 v、方向与两者中心连线垂直。恒星的质量为 M，引力常量为 G。下列说法正确的是（    ）

A．若 v = \(\sqrt {\frac{{GM}}{R}} \)，小星球做匀速圆周运动

B．若 \(\sqrt {\frac{{GM}}{R}} \) < v < \(\sqrt {\frac{{2GM}}{R}} \)，小星球做抛物线运动

C．若 v = \(\sqrt {\frac{{2GM}}{R}} \)，小星球做椭圆运动

D．若 v > \(\sqrt {\frac{{2GM}}{R}} \)，小星球可能与恒星相撞

【答案】

A

 

3．2025 年 4 月 24 日，在甘肃酒泉卫星发射中心成功发射了搭载神舟二十号载人飞船的长征二号 F 遥二十运载火箭。若在初始的 1 s 内燃料对火箭的平均推力约为 6×10⁶ N。火箭质量约为 500 吨且认为在 1 s 内基本不变，则火箭在初始 1 s 内的加速度大小约为（    ）（重力加速度 g 取 10 m/s²）

A．2 m/s²               B．4 m/s²               C．6 m/s²               D．12 m/s²

【答案】

A

 

4．如图，小球 A 从距离地面 20 m 处自由下落，1 s 末恰好被小球 B 从左侧水平击中，小球 A 落地时的水平位移为 3 m。两球质量相同，碰撞为完全弹性碰撞，重力加速度 g 取 10 m/s²，则碰撞前小球 B 的速度大小 v 为（    ）

A．1.5 m/s             B．3.0 m/s

C．4.5 m/s              D．6.0 m/s

【答案】

B

 

5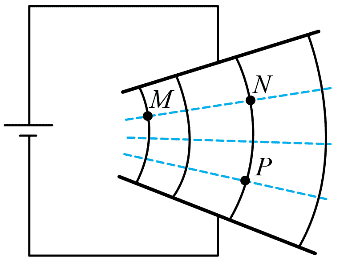．如图，两极板不平行的电容器与直流电源相连，极板间形成非匀强电场，实线为电场线，虚线表示等势面。M、N 点在同一等势面上，N、P 点在同一电场线上。下列说法正确的是（    ）

A．M 点的电势比 P 点的低

B．M 点的电场强度比 N 点的小

C．负电荷从 M 点运动到 P 点，速度增大

D．负电荷从 M 点运动到 P 点，电场力做负功

【答案】

D

 

6．闭合金属框放置在磁场中，金属框平面始终与磁感线垂直。如图，磁感应强度 B 随时间 t 按正弦规律变化。Φ 为穿过金属框的磁通量，E 为金属框中的感应电动势，下列说法正确的是 （    ）

A．t 在 0 ~ \(\frac{T}{4}\) 内，Φ 和 E 均随时间增大

B．当 t = \(\frac{T}{8}\) 与 \(\frac{3T}{8}\) 时，E 大小相等，方向相同

C．当 t = \(\frac{T}{4}\) 时，Φ 最大，E 为零

D．当 t = \(\frac{T}{2}\) 时，Φ 和 E 均为零

【答案】

C

【解析】

A．在 0 ~ \(\frac{T}{4}\) 间内，磁感应强度 B 增加，根据 Φ = BS 则磁通量 Φ 增加，但是图像的斜率减小，即磁感应强度 B 的变化率逐渐减小，根据法拉第电磁感应定律 E = \(\frac{{\Delta B}}{{\Delta t}}\)S 可知，感应电动势 E 逐渐减小，选项 A 错误；

B．当 t = \(\frac{T}{8}\) 与 \(\frac{3T}{8}\) 时，因 B–t 图像的斜率大小相等，符号相反，可知感应电动势 E 大小相等，方向相反，选项 B 错误；

C．t = \(\frac{T}{4}\) 时，B 最大，则磁通量 Φ 最大，但是 B 的变化率为零，则感应电动势 E 为零，选项 C 正确；

D ．t = \(\frac{T}{2}\) 时，B 为零，则磁通量 Φ 为零，但是 B 的变化率最大，则感应电动势 E 最大，选项 D 错误。

故选 C。

 

7．离子注入机是研究材料辐照效应的重要设备，其工作原理如图 1 所示。从离子源 S 释放的正离子（初速度视为零）经电压为 U₁ 的电场加速后，沿 OOʹ 方向射入电压为 U₂ 的电场（OOʹ 为平行于两极板的中轴线）。极板长度为 l、间距为 d，U₂–t 关系如图2所示。长度为 a 的样品垂直放置在距 U₂ 极板 L 处，样品中心位于 Oʹ 点。假设单个离子在通过 U₂ 区域的极短时间内，电压 U₂ 可视为不变，当 U₂ = ±U_m 时。离子恰好从两极板的边缘射出。不计重力及离子之间的相互作用。下列说法正确的是 （    ）

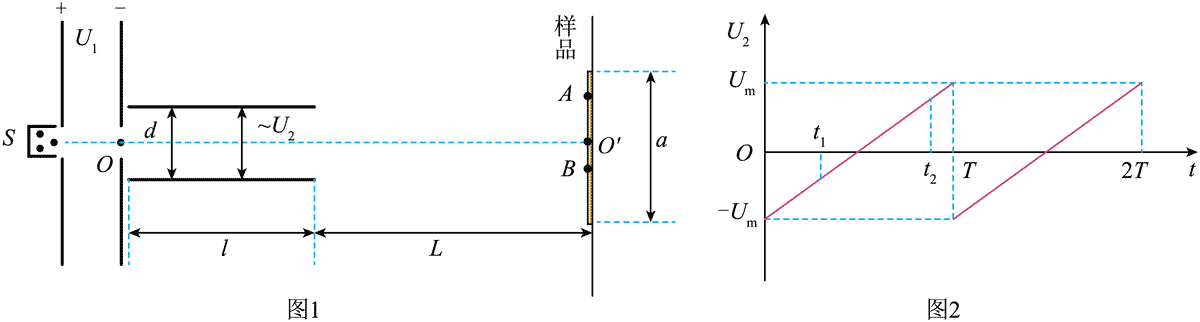
A．U₂ 的最大值 U_m = \(\frac{{{d^2}}}{{{l^2}}}\)U₁

B．当 U₂ = ±U_m 且 L = \(\frac{{(a - d)l}}{{2d}}\) 时，离子恰好能打到样品边缘

C．若其他条件不变，要增大样品的辐照范围，需增大 U₁

D．在 t₁ 和 t₂ 时刻射入 U₂ 的离子，有可能分别打在 A 和 B 点

【答案】

B

 

8．如图，轻质弹簧上端固定，下端悬挂质量为 2m 的小球 A，质量为 m 的小球 B 与 A 用细线相连，整个系统处于静止状态。弹簧劲度系数为 k，重力加速度为 g。现剪断细线，下列说法正确的是（    ）

A．小球 A 运动到弹簧原长处的速度最大

B．剪断细线的瞬间，小球 A 的加速度大小为 \(\frac{g}{2}\)

C．小球 A 运动到最高点时，弹簧的伸长量为 \(\frac{{mg}}{k}\)

D．小球 A 运动到最低点时，弹簧的伸长量为 \(\frac{{2mg}}{k}\)

【答案】

BC

【解析】

A．剪断细线后，弹力大于 A 的重力，则 A 先向上做加速运动，随弹力的减小，则向上的加速度减小，当加速度为零时速度最大，此时弹力等于重力，弹簧处于拉伸状态，选项 A 错误；

B．剪断细线之前则 F_弹 = 3mg

剪断细线瞬间弹簧弹力不变，则对A由牛顿第二定律 F_弹 – 2mg = 2ma

解得 A 的加速度 a = \(\frac{g}{2}\)

选项 B 正确；

C．剪断细线之前弹簧伸长量 x₁ = \(\frac{{3mg}}{k}\)

剪断细线后 A 做简谐振动，在平衡位置时弹簧伸长量 x₂ = \(\frac{{2mg}}{k}\)

即振幅为 A = x₁ – x₂ = \(\frac{{mg}}{k}\)

由对称性可知小球A运动到最高点时，弹簧伸长量为 \(\frac{{mg}}{k}\)，选项 C 正确；

D．由上述分析可知，小球A运动到最低点时，弹簧伸长量为 \(\frac{{3mg}}{k}\)，选项 D 错误。

故选 BC。

 

9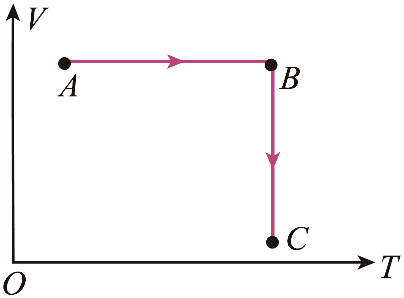．如图，一定量的理想气体从状态 A 经等容过程到达状态 B，然后经等温过程到达状态 C。已知质量一定的某种理想气体的内能只与温度有关，且随温度升高而增大。下列说法正确的是（    ）

A．A→B 过程为吸热过程

B．B→C 过程为吸热过程

C．状态 A 压强比状态 B 的小

D．状态 A 内能比状态 C 的小

【答案】

ACD

【解析】

A．A→B 过程，体积不变，则 W = 0，温度升高，则 ∆U > 0，根据热力学第一定律 ∆U = W + Q 可知 Q > 0，即该过程吸热，选项 A 正确；

B．B→C 过程，温度不变，则 ∆U = 0，体积减小，则 W > 0，根据热力学第一定律 ∆U = W + Q 可知 Q < 0，即该过程为放热过程，选项 B 错误；

C．A→B 过程，体积不变，温度升高，根据查理定律可知，压强变大，即状态 A 压强比状态 B 压强小，选项 C 正确；

D．状态 A 的温度低于状态 C 的温度，可知状态 A 的内能比状态 C 的小，选项 D 正确。

故选 ACD。

 

10．2025 年 5 月 1 日，全球首个实现“聚变能发电演示”的紧凑型全超导托卡马克核聚变实验装置（BEST）在我国正式启动总装。如图是托卡马克环形容器中磁场截面的简化示意图，两个同心圆围成的环形区域内有垂直纸面向里的匀强磁场，磁感应强度大小为 B，内圆半径为 R₀。在内圆上 A 点有 a、b、c 三个粒子均在纸面内运动，并都恰好到达磁场外边界后返回。已知 a、b、c 带正电且比荷均为 \(\frac{q}{m}\)，a 粒子的速度大小为 v_a = \(\frac{{qB{R_0}}}{m}\)，方向沿同心圆的径向；b 和 c 粒子速度方向相反且与 a 粒子的速度方向垂直。不考虑带电粒子所受的重力和相互作用。下列说法正确的是（    ）

A．外圆半径等于 2R₀

B．a 粒子返回 A 点所用的最短时间为 \(\frac{{(3\pi  + 2)m}}{{qB}}\)

C．b、c 粒子返回 A 点所用的最短时间之比为 \(\frac{{\sqrt 2 }}{{\sqrt 2  + 2}}\)

D．c 粒子的速度大小为 \(\frac{{\sqrt 2 }}{2}\)v_a

【答案】

BD

 

11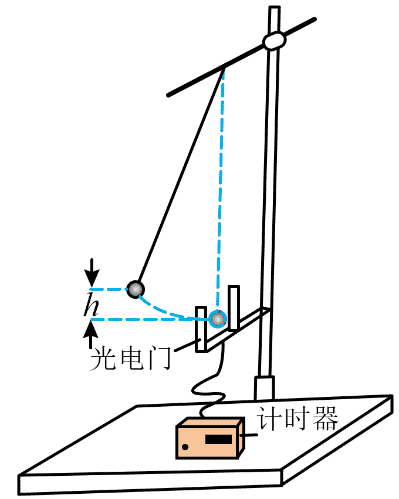．某学习小组使用如图所示的实验装置验证机械能守恒定律。

把一个直径为 d 的小球用不可伸长的细线悬挂，光电门置于小球平衡位置处，其光线恰好通过小球球心，计时器与光电门相连。

将小球拉离平衡位置并记录其高度 h，然后由静止释放（运动平面与光电门光线垂直），记录小球经过光电门的挡光时间 Δt。改变 h，测量多组数据。已知重力加速度为 g，忽略阻力。

（1）以 h 为横坐标、________（填“Δt”、“(Δt)²”、“\(\frac{1}{{\Delta t}}\)”或“\(\frac{1}{{{{(\Delta t)}^2}}}\) ”）为纵坐标作直线图。若所得图像过原点，且斜率为________（用 d 和 g 表示），即可证明小球在运动过程中机械能守恒。

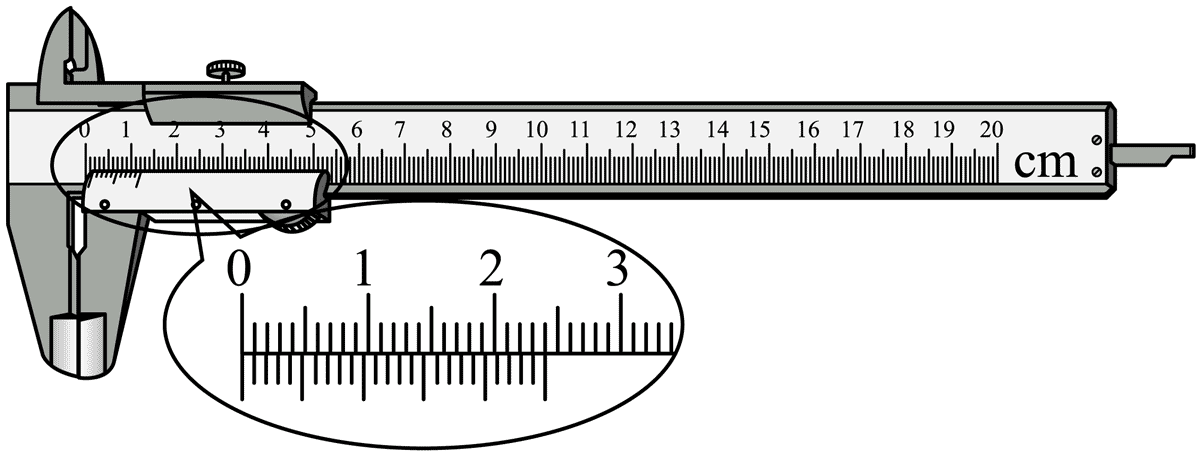
（2）实验中，用游标卡尺测得小球直径 d = 20.48 mm。

①由结果可知，所用的是________分度的游标卡尺（填“10”、“20”或“50）；

②小组设计了一把 25 分度的游标卡尺，未测量时的状态如图所示。如果用此游标卡尺测量该小球直径、则游标尺上第________条刻度线与主尺上的刻度线对齐。

【答案】

（1）\(\frac{1}{{{{(\Delta t)}^2}}}\) ，\(\frac{{2g}}{{{d^2}}}\)

（2）①50      ②12

【解析】

（1）小球经过光电门的挡光时间Δt，可得小球到达平衡位置 v = \(\frac{d}{{\Delta t}}\)

为验证机械能守恒定律，此过程中重力势能转化为动能有 mgh = \(\frac{1}{2}\)mv²

联立解得 \(\frac{1}{{{{(\Delta t)}^2}}}\) = \(\frac{{2g}}{{{d^2}}}\)h

可得纵坐标为 \(\frac{1}{{{{(\Delta t)}^2}}}\)

图像的斜率为 k = \(\frac{{2g}}{{{d^2}}}\)。

（2）10 分度、20 分度、50 分度的游标卡尺的精确度分别为 0.1 mm、0.05 mm、0.02 mm。此游标卡尺测得小球直径 d = 20.48 mm，可以判断所用的是 50 分度的游标卡尺。

若为 25 分度的游标卡尺，其精确度为 0.04mm，用此游标卡尺测量该小球直径，可得

n = \(\frac{0.48}{0.04}\) = 12

则游标尺上第 12 条刻度线与主尺上的刻度线对齐。

 

12．某兴趣小组设计测量电阻阻值的实验方案。可用器材有：电池（电动势 1.5 V）两节，电压表（量程 3 V，内阻约 3 kΩ），电流表（量程 0.3 A，内阻约 1 Ω），滑动变阻器（最大阻值 20 Ω），待测电阻 R_x，开关 S₁，单刀双掷开关 S₂，导线若干。

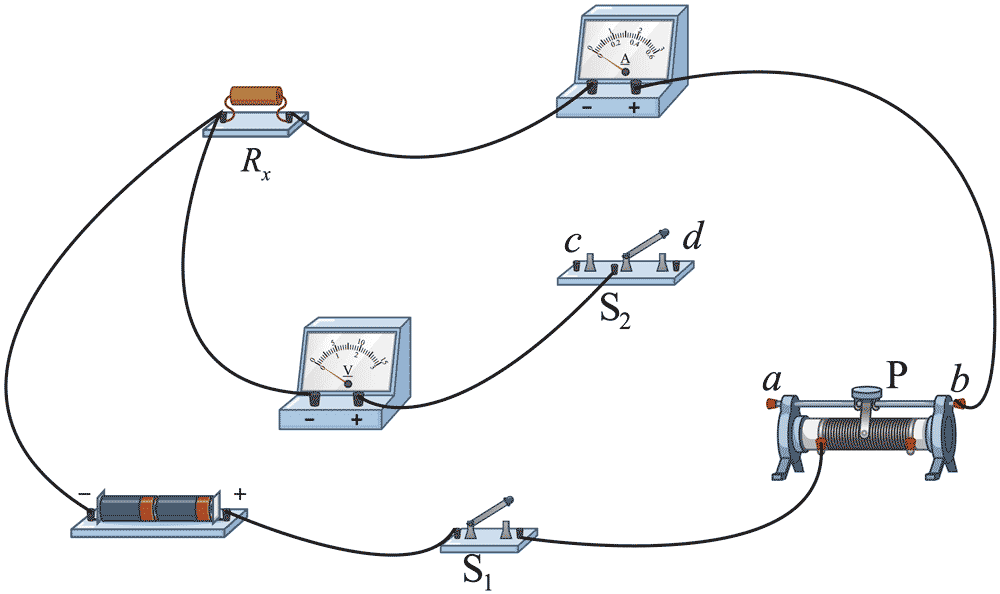
（1）首先设计如上图所示的电路。

①要求用 S₂ 选择电流表内、外接电路，请在图1中补充连线将 S₂ 的 c、d 端接入电路____；

②闭合 S₁ 前，滑动变阻器的滑片 P 应置于___端（填“a”或“b”）；

③闭合 S₁ 后，将 S₂ 分别接 c 和 d 端，观察到这两种情况下电压表的示数有变化、电流表的示数基本不变，因此测量电阻时 S₂ 应该接______端（填“c”或“d”）。

（2）为了消除上述实验中电表引入的误差、该小组又设计了如图所示的电路。

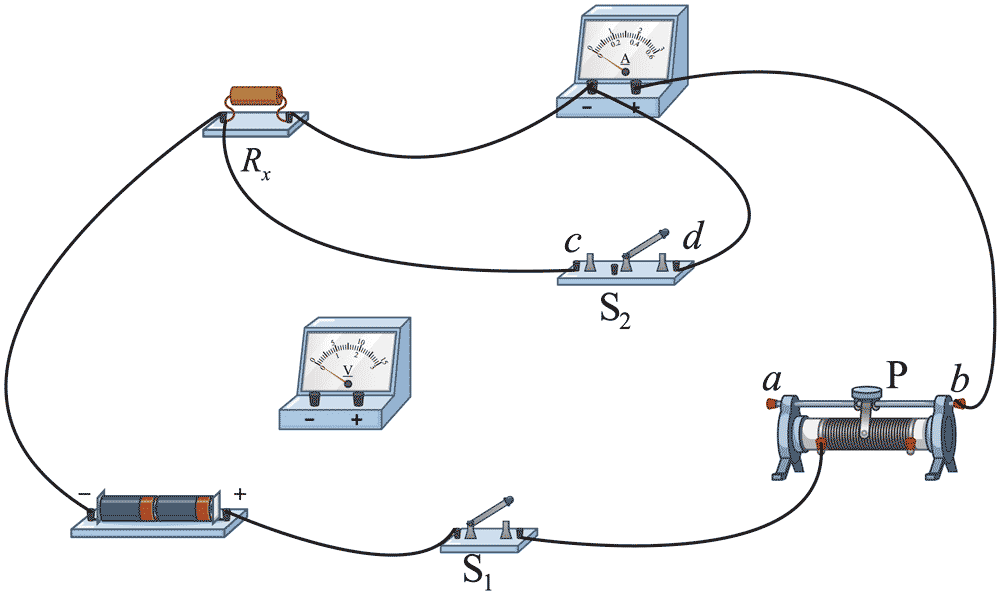
①请在上图中补充连线将电压表接入电路______；

②闭合 S₁，将 S₂ 分别接 c 和 d 端时，电压表、电流表的读数分别为 U_c、I_c 和 U_d、I_d。则待测电阻阻值 R_x =_______（用 U_c、U_d、I_c 和 I_d 表示）。

【答案】

（1）①如图

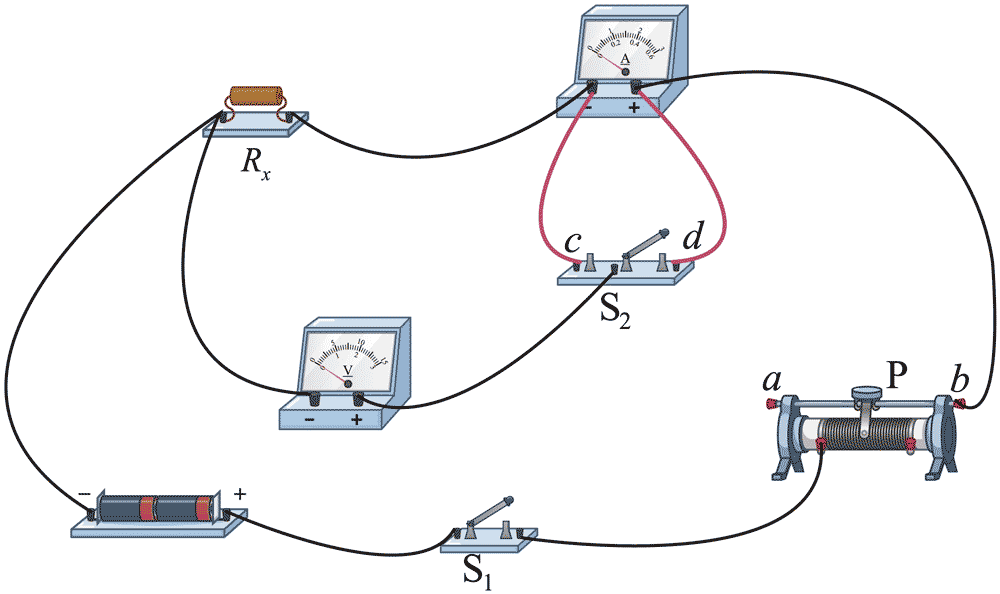
②b          ③c

（2）①如图

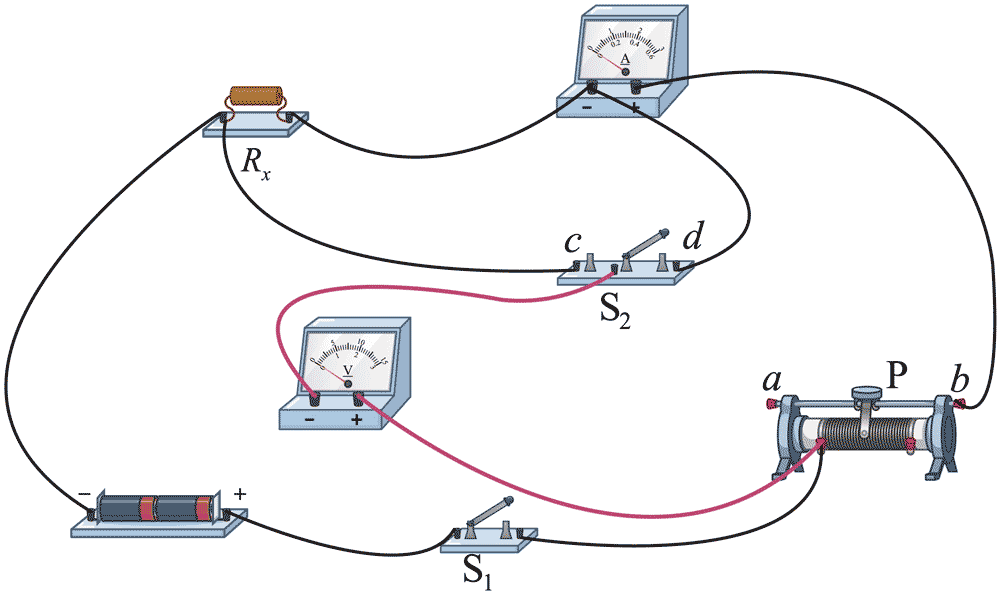
②\(\frac{{{U_{\rm{c}}}}}{{{I_{\rm{c}}}}}\) − \(\frac{{{U_{\rm{d}}}}}{{{I_{\rm{d}}}}}\)

【解析】

（1）实物连接图如图所示。

闭合 S₁ 前，根据滑动变阻器的限流式接法，滑片 P 应置于 b 端，连入电路中的阻值最大，保护电路的安全。

闭合 S₁ 后，将 S₂ 分别接 c 和 d 端，观察到这两种情况下电压表的示数有变化、电流表的示数基本不变，说明电流表分压明显，为减小实验误差，应采用电流表外接法，因此测量电阻时 S₂ 应该接 c 端。

（2）实物连接图如图所示，

根据电路分析，当闭合 S₁，将 S₂ 接 c 端时，电压表、电流表的读数分别为 U_c、I_c，则

\(\frac{{{U_{\rm{c}}}}}{{{I_{\rm{c}}}}}\) = R_x + R_A + R_滑

将 S₂ 接 d 端时，电压表、电流表的读数分别为 U_d、I_d，则

\(\frac{{{U_{\rm{d}}}}}{{{I_{\rm{d}}}}}\) = R_A + R_滑

那么待测电阻阻值R_x =  \(\frac{{{U_{\rm{c}}}}}{{{I_{\rm{c}}}}}\) − \(\frac{{{U_{\rm{d}}}}}{{{I_{\rm{d}}}}}\) 。

 

13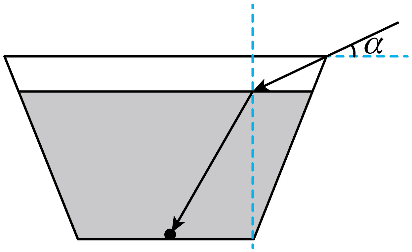．已知一圆台容器，高 H = 15 cm，上口径 R = 13 cm，容器底部中心有一质点，未装入水时，人眼从容器边缘无法观测到该质点，装入某种液体后，恰好可以看到，此时液面高度 h = 12 cm，人眼观测角度 α 满足 sin α = \(\frac{3}{5}\)，人眼到入射处距离为 5 cm。光在真空中的传播速度 c = 3.0×10⁸ m/s，求：

（1）该液体的折射率；

（2）光从底部质点反射至人眼全过程的时间。

【答案】

（1）\(\frac{4}{3}\)

（2）1×10⁻⁹ s

 

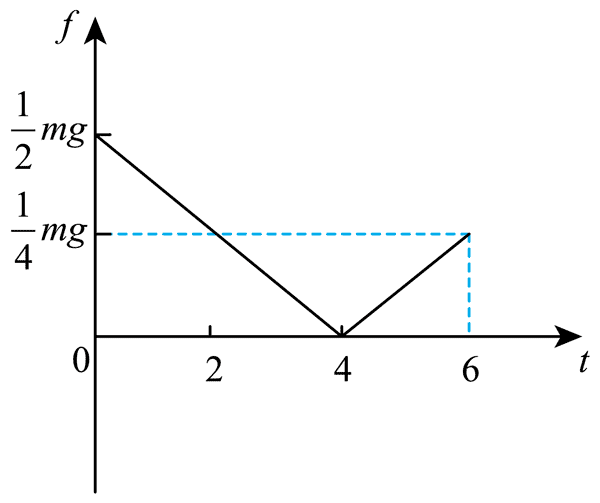
14．如图1所示，细杆两端固定，质量为 m 的物块穿在细杆上。初始时刻。物块刚好能静止在细杆上。现以水平向左的力 F 作用在物块上，F 随时间 t 的变化如图 2 所示。开始滑动瞬间的滑动摩擦力等于最大静摩擦力。细杆足够长，重力加速度为 g，θ = 30°。求 ：

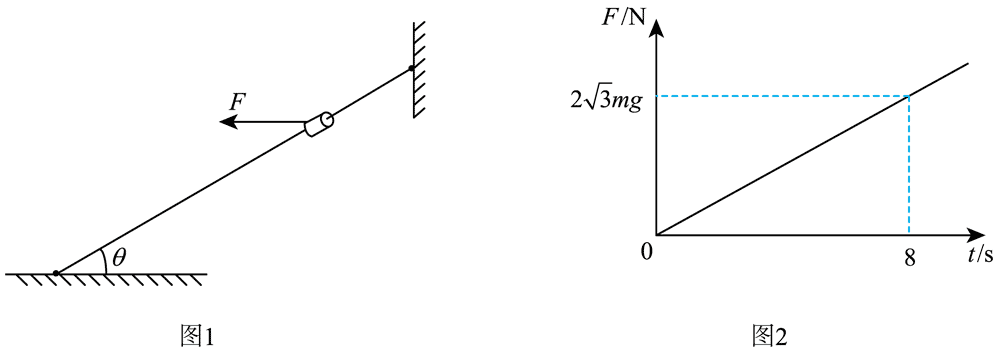
（1）t = 6 s 时 F 的大小，以及 t 在 0 ~ 6 s 内 F 的冲量大小。

（2）t 在 0 ~ 6 s 内，摩擦力 f 随时间 t 变化的关系式，并作出相应的 f−t 图像。

（3）t = 6 s 时，物块的速度大小。

【答案】

（1）F = \(\frac{{3\sqrt 3 mg}}{2}\)，I = \(\frac{{9\sqrt 3 mg}}{2}\)

（2）f = \(\left( {\frac{1}{2} - \frac{1}{8}t} \right)\)mg（0 ≤ t ≤ 4）

f = \(\left( {\frac{1}{8}t - \frac{1}{2}} \right)\)mg（4 ≤ t ≤ 6）

相应的 f−t 图像如图

（3）v = \(\frac{{17}}{2}\)g

 

15．在自动化装配车间，常采用电磁驱动的机械臂系统，如图，ab、cd 为两条足够长的光滑平行金属导轨，间距为 L，电阻忽略不计。导轨置于磁感应强度大小为 B，方向垂直纸面向里的匀强磁场中，导轨上有与之垂直并接触良好的金属机械臂 1 和 2，质量均为 m，电阻均为 R。导轨左侧接有电容为 C 的电容器。初始时刻，机械臂 1 以初速度 v₀ 向右运动，机械臂 2 静 止，运动过程中两机械臂不发生碰撞。系统达到稳定状态后，电流为零，两机械臂速度相同。

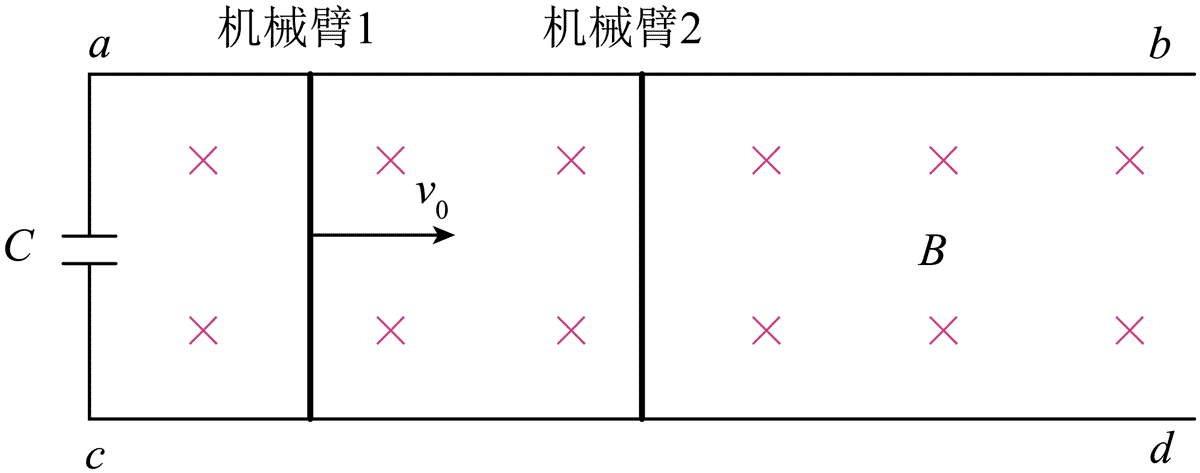
（1）求初始时刻机械臂 1 的感应电动势大小和感应电流方向；

（2）系统达到稳定状态前，若机械臂 1 和 2 中的电流分别为 I₁ 和 I₂，写出两机械臂各自所受安培力的大小；若电容器两端电压为 U，写出电容器电荷量的表达式；

（3）稳系统达到稳定状态后两机械臂的速度。若要两机械臂不相撞，二者在初始时刻的间距至少为多少？

【答案】

（1）BLv₀，沿机械臂1向上

（2）BI₁L，BI₂L，Q = CU

（3）\(\frac{{m{v_0}}}{{C{B^2}{L^2} + 2m}}\)，方向向右；\(\frac{{m{v_0}R}}{{{B^2}{L^2}}}\)