1．“风动石”是福建省著名的自然景观，如图所示。无风时，“风动石”在重力和底部巨石作用力 F₁ 的作用下静止不动。若“风动石”受到一水平方向的风力作用时仍保持静止，此时底部巨石对其作用力为 F₂，则（    ）

A．F₁ 的大小比 F₂ 的小      B．F₁ 的大小比 F₂ 的大

C．F₁ 与 F₂ 大小相等          D．F₁ 与 F₂ 方向相同

【答案】

A

 

2．在图（a）所示电路中，理想变压器原、副线圈匝数比 4∶1，电阻 R₁ 的阻值为 R₂ 的 2 倍，电压表为理想电压表。若原线圈输入如图（b）所示的正弦交流电，则（    ）

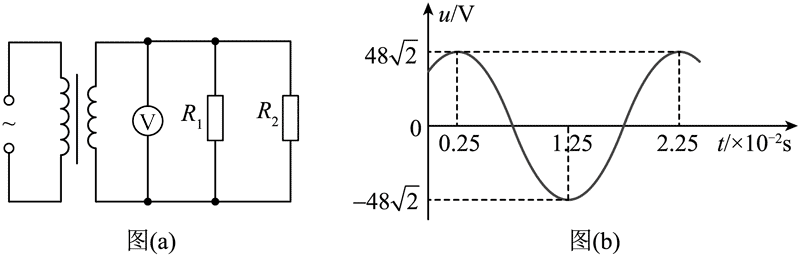
A．交流电周期为 2.25 s

B．电压表示数为 12 V

C．流经副线圈的电流是流经 R₁ 的 2 倍

D．变压器的输入、输出功率之比为 4∶1

【答案】

B

 

3．如图，两根长直细导线 L₁、L₂ 平行放置，其所在平面上有 M、O、N 三点，O 为线段 MN 的中点，L₁、L₂ 分别处于线段 OM、ON 的中垂线上。当 L₁、L₂ 通有大小相等、方向相反的电流时，M、O 点的磁感应强度大小分别为 B₁、B₂。现保持 L₁ 的电流不变，撤去 L₂ 的电流，此时 N 点的磁感应强度大小为（    ）

A．\(\frac{{{B_2}}}{2}\) − B₁           B．B₂ − \(\frac{{{B_1}}}{2}\)             C．\(\frac{1}{2}\)（B₂ − B₁）              D．B₂ − B₁

【答案】

A

 

4．角分辨光电子能谱仪是现代科学研究的先进仪器，其核心装置中有两个同心半球极板。垂直半球底面且过球心 O 的截面如图所示。极板间存在一径向电场，其等势线为一系列以 O 为圆心的半圆。电子 a 以初动能 E_k，从入口 M 点垂直半球底面入射，从 N 点射出，电子 b 也从 M 点垂直半球底面入射，经 P 点后从 Q 点射出。两电子的运动轨迹如图所示，已知电子 a 轨迹为一以 O 为圆心的半圆，与 OP 交于 H 点，H、P 两点间的电势差为 U，OM = r，NQ = 2HP，电子电荷量大小为 e，重力不计。则（    ）

A．B 点的电场强度 E = \(\frac{{{2E_{\rm{k}}}}}{{er}}\)

B．电子 a 在 H 点受到的电场力大小为 \(\frac{{{E_{\rm{k}}}}}{{r}}\)

C．电子 b 在 P 点动能小于在 Q 点动能

D．电子 b 从 M 点运动到 Q 点的过程中，克服电场力所做的功小于 2eU

【答案】

D

 

5．在 2025 年央视春晚上，人形机器人表演了一个精彩的扭秧歌、转手绢节目。如图，机器人转动手绢，手绢绕其中心点 O 在一竖直面内匀速转动，O 点在空间中保持不动，P、Q 是固定在手绢上可视为质点的两个小饰物，与 O 点的距离分别为 d、\(\sqrt 3 \)d，则手绢转动过程（    ）

A．Q 的线速度大小是 P 的 \(\sqrt 3 \) 倍

B．Q 的角速度大小是 P 的 \(\sqrt 3 \) 倍

C．P 的加速度大小是 Q 的 \(\sqrt 3 \) 倍

D．P 点所受合外力方向始终指向 O 点

【答案】

AD

 

6．2025 年，我国“人造太阳”实现了等离子体原子核温度超1亿度的突破。在 1 亿度的高温条件下“人造太阳”内可发生如下核反应：²₁H + ³₁H→⁴₂He + ¹₀n + 17.5 MeV，若动量大小相等，方向相反的氘核与氚核正碰后发生核反应，反应产生的为 ⁴₂He 与 ¹₀n 的总动能近似等于核反应释放的全部能量，则（    ）

A．该反应有质量亏损

B．该反应为核裂变反应

C．¹₀n 获得的动能约为 14 MeV

D．⁴₂He 获得的动能约为 14 MeV

【答案】

AC

 

7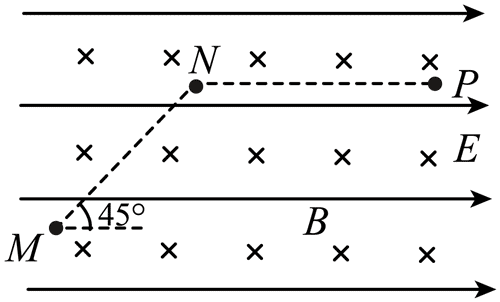．如图，真空中存在一水平向右的匀强电场，同时存在一水平且垂直纸面向里的匀强磁场。一质量为 m、电量为 q（q > 0）的带电微粒从 M 点以初速度 v 入射，沿着 MN 做匀速直线运动。微粒到 N 点时撤去磁场，一段时间后微粒运动到 P 点。已知 M、N、P 三点处于同一竖直平面内，MN 与水平方向呈 45°，N 点与 P 等高，重力加速度为 g，则（    ）

A．电场强度大小为 \(\frac{{\sqrt 2 mg}}{q}\)

B．磁感应强度大小为 \(\frac{{\sqrt 2 mg}}{{qv}}\)

C．NP 两点的电势差为 \(\frac{{2m{v^2}}}{q}\)

D．从 N 点运动到 P 的过程中，微粒到直线 NP 的最大距离为 \(\frac{{{v^2}}}{{8g}}\)

【答案】

BC

【解析】

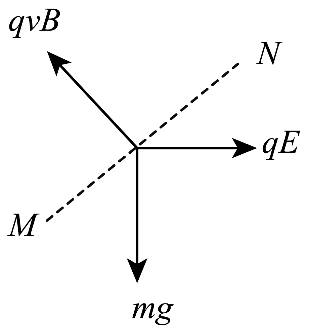AB、带电体在复合场中能沿着 MN 做匀速直线运动，可知粒子受力情况如图所示。

由受力平衡可知

mg = qE，qvB = mg

解得电场强度E = \(\frac{{mg}}{q}\)，磁感应强度B = \(\frac{{\sqrt 2 mg}}{{qv}}\)，故 A 错误，B 正确。

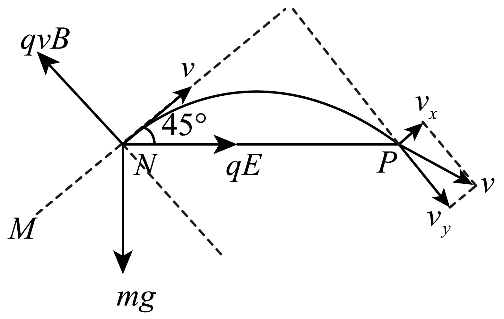C、在 N 点撤去磁场后，粒子受力方向与运动方向垂直，做类平抛运动，如图所示。且加速度

a = \(\frac{{{F_合}}}{m}\) = \(\sqrt 2 \)g

粒子到达P点时，位移偏转角为45°，故在 P 点，速度角的正切值

tanθ = 2tan45° = 2

…………

 

8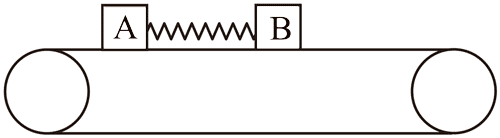．如图，物块 A、B 用轻弹簧连接并放置于水平传送带上，传送带以 1 m/s 的恒定速率顺时针转动。t = 0 时，A 的速度大小为 2 m/s，方向水平向右，B 的速度为 0，弹簧处于原长，t = t₁ 时（t₁ 为未知量），A 第一次与传送带共速，弹簧弹性势能 0.75 J。已知 A、B 可视为质点，质量分别为 1 kg、2 kg，与传送带的动摩擦因数为 0.5、0.25；A 与传送带相对滑动时会留下痕迹，重力加速度大小取 g = 10 m/s²，A、B 始终在传送带上，弹簧始终在弹性限度内，则（    ）

A．在 t = \(\frac{{{t_0}}}{2}\) 时，A 的加速度大小比 B 的小

B．t = t₁ 时，B 的速度大小为 0.5 m/s

C．t = t₁ 时，弹簧的压缩量为 0.2 m

D．0 ~ t₁ 过程中，A 在传送带上留下的划痕长度小于 0.05 m

【答案】

BD

 

9．某智能洗衣机液位控制原理如图所示。洗衣缸中的水将一定质量的空气封闭在与底部相连的细管中，洗衣机通过压力传感器感知管中空气压强，从而控制水位。假设细管粗细均匀，进排水过程管中空气为理想气体，温度不变。某次排水过程中，管中封闭空气的压强为 p₁ 时，空气柱长度为 L；当封闭空气的压强为 p₂ 时，空气柱长度为___________，排水过程管中空气对外___________。（填“做正功”，“做负功”，“不做功”）

【答案】

\(\frac{{{p_1}}}{{{p_2}}}\)L₁，做正功

【解析】

设细管的截面积为S，根据玻意耳定律有

p₁L₁S = p₂L₂S

可得L₂ = \(\frac{{{p_1}}}{{{p_2}}}\)L₁

根据题意当洗衣机内的水位下降时，空气柱长度变长，故内部气体对外界做正功。

 

10．沙蝎能灵敏地感知外界的振动信号，可通过沙子传来的波定位波源位置。一沙蝎先后感知到波源某次振动产生的沿直线传来的纵波和横波，该纵波和横波频率相同，传播速度大小分别为 v₁ 和 v₂，且 v₁ 大于 v₂，则纵波波长___________（填“大于”小于”或“等于”）横波波长。若沙蝎感知到纵波和横波的时间差为 Δt，则沙蝎与波源的距离为___________。

【答案】

大于，\(\frac{{{v_1}{v_2}\Delta t}}{{{v_1} - {v_2}}}\)

【解析】

根据公式 v = λf，由于纵波速度大于横波速度，频率相同，故可知纵波波长大于横波波长；

设波源与蝎子的距离为 s，根据题意可知 \(\frac{s}{{{v_2}}}\) − \(\frac{s}{{{v_1}}}\) = Δt

解得 s = \(\frac{{{v_1}{v_2}\Delta t}}{{{v_1} - {v_2}}}\)

 

11．如图，M、N、P 是竖直平面内一直角三角形的三个顶点，M、N 在同一水平线上，∠PMN = 30°。M、N 点分别固定有电荷量为 Q₁、Q₂ 的正点电荷。若一带电小球置于 P 点时，处于受力平衡状态，则 Q₁ 与 Q₂ 的比值为___________，除 P 点外，线段 MP 上___________（填“存在”或“不存在”）该带电小球受力平衡的其他点。

【答案】

\(\sqrt 3 \)∶1，不存在

 

12．某实验小组探究糖水折射率 n 随浓度 η 的变化规律。主要装置包括激光器和长方体玻璃缸，玻璃缸正面内侧刻有水平、竖直标尺，如图（a）所示。实验操作过程如下：

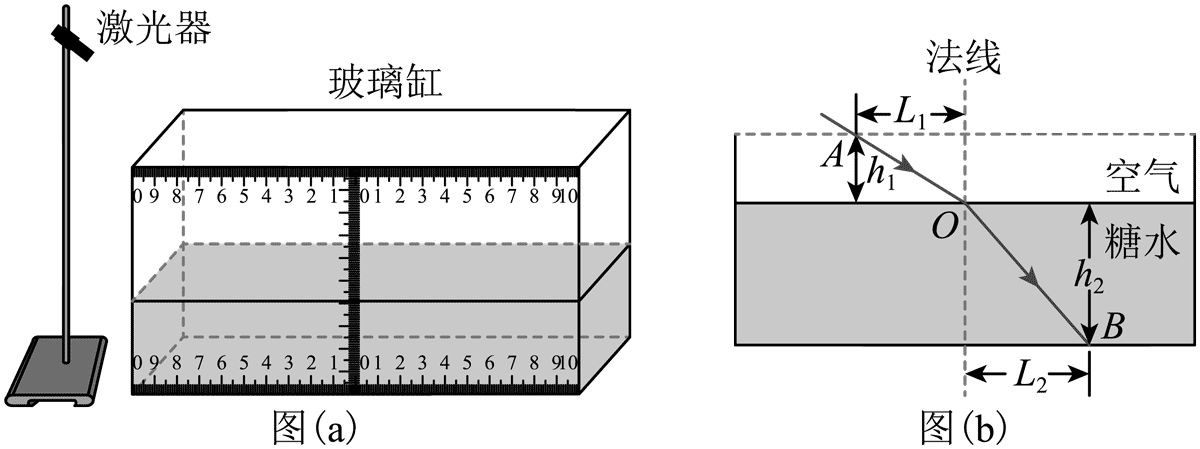
（1）调配一定浓度的糖水，注入水平放置的玻璃缸中。

（2）打开激光器，让激光紧贴玻璃缸正面内侧以一定入射角从空气折射入糖水。

（3）调整激光器，使入射点 O 处于竖直刻度尺的正后方，光路如图（b）所示，其中 A 点是入射光线与玻璃缸上边沿所在平面的交点，B 点是折射光线与玻璃缸底部的交点，A、B 点到法线的距离分别为 L₁、L₂，到液面的距离分别为 h₁、h₂。测得 L₁、L₂、h₁、h₂ 的值，并利用表达式 n =________（用 L₁、L₂、h₁、h₂ 表示）求出糖水折射率。

（4）改变缸内糖水浓度，进行多次实验，将实验数据填入下表。

浓度 η/%	11.8	21.1	32.0	39.1	51.1
折射率 n	1.34	1.36	1.38	1.40	1.42

（5）在图（c）给出的坐标纸上补上浓度 η = 32% 的数据点。分析图中数据点，可知糖水折射率随浓度近似线性变化，绘制出“n–η”图线________。

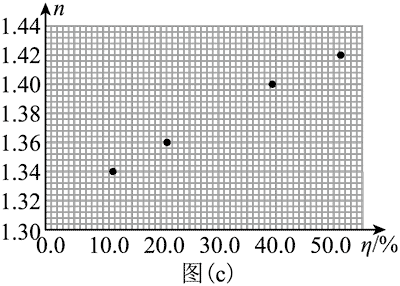
（6）由所绘图线可知，糖水浓度每增加 10.0%，折射率增大________。（结果保留 2 位有效数字）

【答案】

（1）\(\frac{{{L_1}\sqrt {L_2^2 + h_2^2} }}{{{L_2}\sqrt {L_1^2 + h_1^2} }}\)

（5）

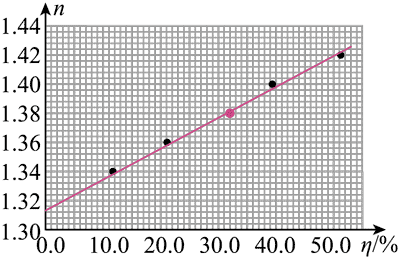
（6）0.020

 

13．某实验小组基于“等效替代法”设计了如图（a）所示的电路用于电阻测量。使用的器材有：电源 E（电动势 3 V），电流表 A（量程 30 mA），定值电阻 R₁、R₂、R₃（阻值均为 100 Ω），定值电阻 R₄（阻值 200 Ω），滑动变阻器 R₅（最大阻值 200 Ω，额定电流 1.5 A），带标尺的滑动变阻器 R₆（最大阻值 100 Ω，额定电流 1.5 A），选择开关 S₁，单刀开关 S₂，待测电阻 R_x（阻值小于 400 Ω），导线若干。

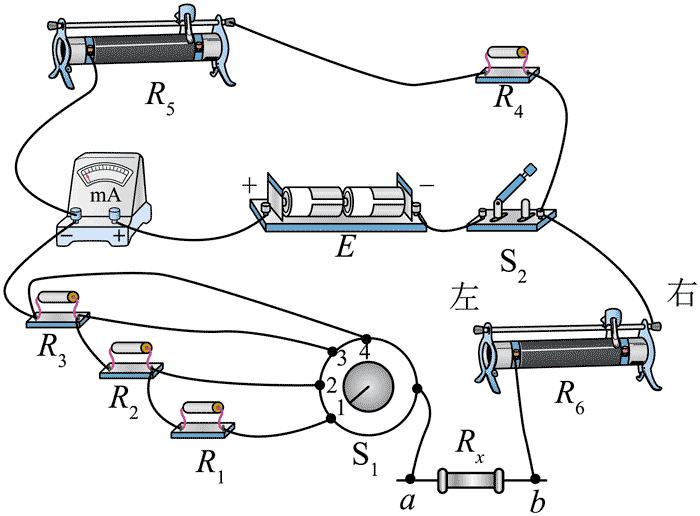
（1）按照图（a），将图（b）中的实物连线补充完整________；

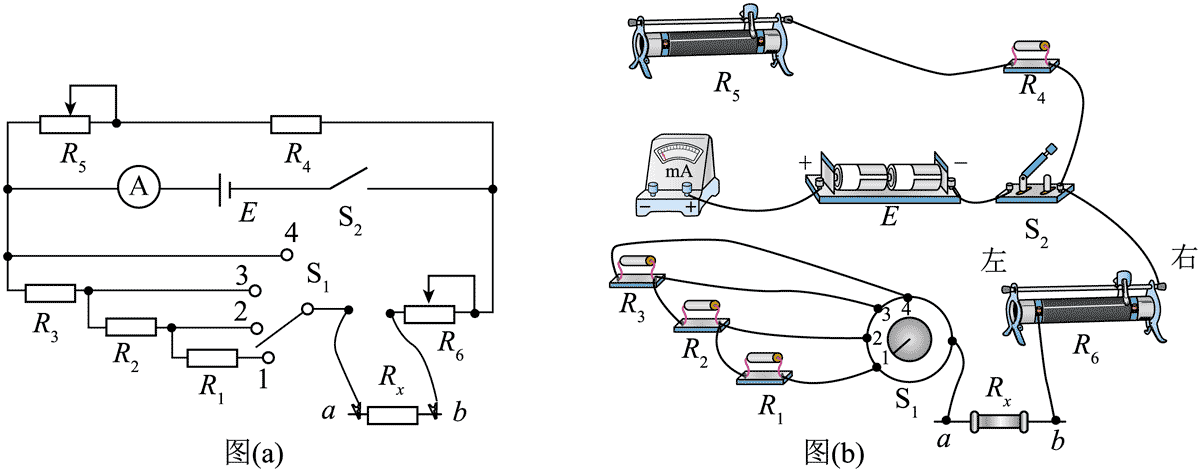
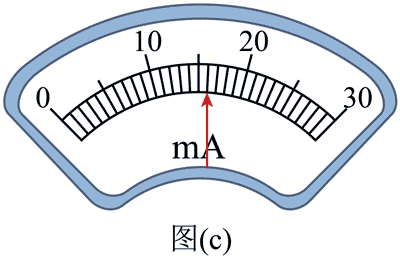（2）将鳄鱼夹 a、b 短接，滑动变阻器 R₆ 的滑片移至最右端刻度处，S₁ 打在位置 1。接通 S₂，调节滑动变阻器 R₅，电流表指针指在图（c）所示的位置，记录电流表示数 I =________mA，此示数作为本次实验的电流定标值；

（3）断开 S₁、S₂，用鳄鱼夹 a、b 夹住 R_x 两端。接通 S₂，将 S₁ 依次打在位置 1、2，发现电流表示数均小于定标值 I；S₁ 打到位置 3 时，电流表示数大于定标值 I，由此确定 R_x 的阻值范围为________Ω。（填“0 ~ 100”“100 ~ 200”“200 ~ 300”或“300 ~ 400”）；

（4）将 S₁ 重新打在位置________（填“1”“2”或“3”），向左调节滑动变阻器 R₆ 的滑片，直到电流表指针重新回到定标值位置，此时 R₆ 的滑片处于 55 Ω 刻度处。基于“等效替代法”原理，可得 R_x 的阻值为________Ω；

（5）以下因素可能影响测量结果的有________。（多选，填正确答案标号）

A．电源存在内阻                             B．电流表存在内阻

C．滑动变阻器 R₆ 读数有偏差           D．步骤（4）电流表指针未重新回到定标值位置

【答案】

（1）

（2）16.0，15.9，16.1

（3）100 ~ 200

（4）2，145

（5）CD

 

14．在 2024 年巴黎奥运会上，我国游泳运动员创造了男子百米自由泳新的世界纪录。在此次比赛中，运动员起跳后于 t₀ 时刻入水。入水后的运动过程可近似分为三个阶段：t₀ ~ t₁ 段的前程游为匀减速直线运动，t₁ ~ t₂ 段为匀速游，t₂ ~ t₃ 段的冲刺游为匀加速直线运动；速率 v 随时间 t 变化的图像如图所示。已知 t₀ = 0.9 s，t₁ = 10.4 s，t₂ = 44.4 s，t₃ = 46.4 s，求该运动员在

（1）t₀ ~ t₁段的平均速度大小；

（2）t₂ ~ t₃段的加速度大小；

（3）t₂ ~ t₃段的位移大小。

【答案】

（1）2.4 m/s

（2）0.1 m/s²

（3）4.2 m

 

15．如图（a），竖直平面内，一长度大于 4 m 的水平轨道 OP 与光滑半圆形轨道 PNM 在 P 点平滑连接，固定在水平地面上。可视为质点的 A、B 两小物块靠在一起，静置于轨道左端。现用一水平向右推力 F 作用在 A 上，使 A、B 向右运动。以 x 表示 A 离开初始位置的位移，F 随 x 变化的图像如图（b）所示。已知 A、B 质量均为 0.2 kg，A 与水平轨道间的动摩擦因数为 0.25，B 与水平轨道间的摩擦不计，重力加速度大小取 10 m/s²。

（1）求 A 离开初始位置向右运动 1 m 的过程中，推力 F 做的功；

（2）求 A 的位移为 1 m 时，A、B 间的作用力大小；

（3）若 B 能到达 M 点，求半圆形轨道半径应满足的条件。

【答案】

（1）1.5 J

（2）0.5 N

（3）r ≤ 0.2 m

 

16．水平地面上固定有一倾角为 30° 的绝缘光滑斜面，其上有两个宽度分别为 l₁、l₂ 的条形匀强磁场区域 Ⅰ、Ⅱ，虚线为磁场边界，均与斜面底边平行，两区域磁场的磁感应强度大小相等、方向均垂直斜面向上，示意图如图所示。一质量为 m、电阻为 R 的正方形细导线框 abcd 置于区域 Ⅰ 上方的斜面上，cd 边与磁场边界平行。线框由静止开始下滑，依次穿过区域 Ⅰ、区域 Ⅱ。已知 cd 边进入 Ⅰ 到 ab 边离开 Ⅰ 的过程中，线框速度恒为 v，cd 边进入区域 Ⅱ 和 ab 边离开区域 Ⅱ 时的速度相同；区域 Ⅰ、Ⅱ 间的无磁场区域宽度大于线框边长，线框各边材料相同、粗细均匀；下滑过程线框形状不变且始终处于斜面内，cd 边始终与磁场边界平行；重力加速度大小为 g。求：

（1）初始时 cd 边与 Ⅰ 区域上边界的距离；

（2）cd 边进入区域 Ⅰ 后瞬间，cd 两端的电势差；

（3）cd 边进入区域 Ⅱ 和 ab 边离开区域 Ⅱ 的过程中，线框克服安培力做功的平均功率。

【答案】

（1）\(\frac{{{v^2}}}{g}\)

（2）\(\frac{3}{4}\sqrt {\frac{{mgRv}}{2}} \)

（3）若 l₂ > l₁，则 P = \(\frac{{mgv({l_1} + {l_2})}}{{4{l_1}}}\)；若 l₂ < l₁，则 P = \(\frac{{mgv({l_1} + {l_2})}}{{4{l_2}}}\)