1．PET（正电子发射断层成像）是核医学科重要的影像学诊断工具，其检查原理是将含放射性同位素（如：¹⁸₉F）的物质注入人体参与人体代谢，从而达到诊断的目的。¹⁸₉F 的衰变方程为 ¹⁸₉F→X + ⁰₁e + ⁰₀ν，其中 ⁰₀ν 是中微子。已知 ¹⁸₉F 的半衰期是 110 分钟。下列说法正确的是（    ）

A．X 为 ¹⁷₈O                                                  B．该反应为核聚变反应

C．1 克 ¹⁸₉F 经 110 分钟剩下 0.5 克 ¹⁸₉F    D．该反应产生的 ⁰₀ν 在磁场中会发生偏转

【答案】

C

【解析】

A．根据质量数与电荷数守恒可知，该物质为 ¹⁸₈O，故 A 错误；

B．核聚变是轻核结合成重核的过程（如氢弹原理）。本题中的衰变是单个原子核自发转变为另一种原子核，属于放射性衰变（具体为 β⁺ 衰变），而非核聚变，故 B 错误；

C．1 g 该物质经过 110 min 即一个衰变周期，则有一半发生衰变，该物质质量变为 0.5 g，故 C 正确；

D．⁰₀ν 不带电，在磁场中不偏转，故 D 错误。

故选 C。

 

2．甲、乙两行星绕某恒星做圆周运动，甲的轨道半径比乙的小。忽略两行星之间的万有引力作用，下列说法正确的是（    ）

A．甲运动的周期比乙的小                 B．甲运动的线速度比乙的小

C．甲运动的角速度比乙的小             D．甲运动的向心加速度比乙的小

【答案】

A

 

3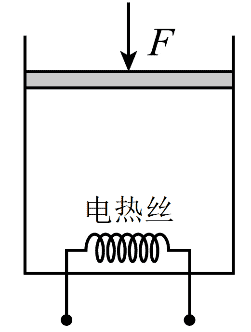．如图所示，内壁光滑的汽缸内用活塞密封一定量理想气体，汽缸和活塞均绝热。用电热丝对密封气体加热，并在活塞上施加一外力 F，使气体的热力学温度缓慢增大到初态的 2 倍，同时其体积缓慢减小。关于此过程，下列说法正确的是（    ）

A．外力 F 保持不变             B．密封气体内能增加

C．密封气体对外做正功     D．密封气体的末态压强是初态的2倍

【答案】

B

【解析】

A．气体温度升高，体积减小，根据 \(\frac{{pV}}{T}\) = C 可知气体压强变大，则外力 F 增加，选项 A 错误；

B．气体温度升高，则气体内能变大，即 ∆U 增加，选项 B 正确；

C．气体体积减小，则外界对气体做功，选项 C 错误；

D．根据 \(\frac{{pV}}{T}\) = C，热力学温度变为原来的 2 倍，体积减小，则气体压强大于原来的 2 倍，选项 D 错误。

故选 B。

 

4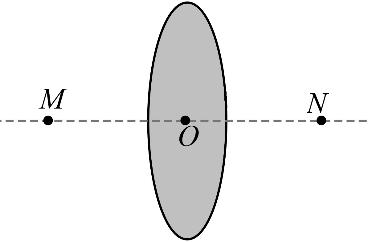．如图所示，在磁感应强度大小为 B 的匀强磁场中，放置一通电圆线圈，圆心为 O 点，线圈平面与磁场垂直。在圆线圈的轴线上有 M 和 N 两点，它们到 O 点的距离相等。已知 M 点的总磁感应强度大小为零，则 N 点的总磁感应强度大小为（    ）

A．0               B．B               C．2B             D．3B

【答案】

A

【解析】

由右手螺旋定则及对称性可知，环形电流在 N 点产生的磁场，磁感应强度与 M 点等大同向。由于 M 点磁感应强度为零，由矢量合成法则可知环境中匀强磁场与 M 点磁场等大反向，即匀强磁场与 N 点的磁场等大反向，N 点的磁感应强度为0。

故选 A。

 

5．如图（a）所示，相距 L 的两足够长平行金属导轨放在同一水平面内，两长度均为 L、电阻均为 R 的金属棒 ab、cd 垂直跨放在两导轨上，金属棒与导轨接触良好。导轨电阻忽略不计。导轨间存在与导轨平面垂直的匀强磁场，其磁感应强度大小 B 随时间变化的图像如图（b）所示，t = T 时刻，B = 0。t = 0 时刻，两棒相距 x₀，ab 棒速度为零，cd 棒速度方向水平向右，并与棒垂直，则 0 ~ T 时间内流过回路的电荷量为（    ）

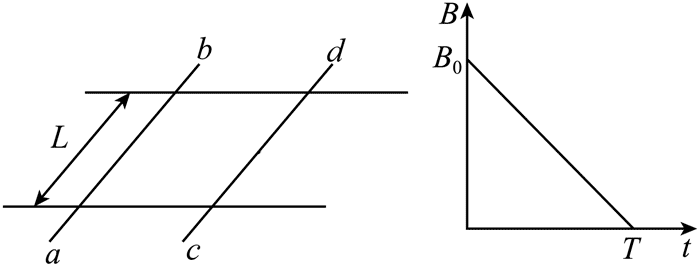
A．\(\frac{{{B_0}L{x_0}}}{{4R}}\)              B．\(\frac{{{B_0}L{x_0}}}{{2R}}\)              C．\(\frac{{{B_0}L{x_0}}}{{R}}\)              D．\(\frac{{2{B_0}L{x_0}}}{{R}}\)

【答案】

B

 

6．某网球运动员两次击球时，击球点离网的水平距离均为 L，离地高度分别为 \(\frac{L}{2}\)、L，网球离开球拍瞬间的速度大小相等，方向分别斜向上、斜向下，且与水平方向夹角均为 θ。击球后网球均刚好直接掠过球网，运动轨迹平面与球网垂直，忽略空气阻力，tanθ 的值为（    ）

A．\(\frac{1}{2}\)             B．\(\frac{1}{3}\)             C．\(\frac{1}{4}\)             D．\(\frac{1}{6}\)

【答案】

C

 

7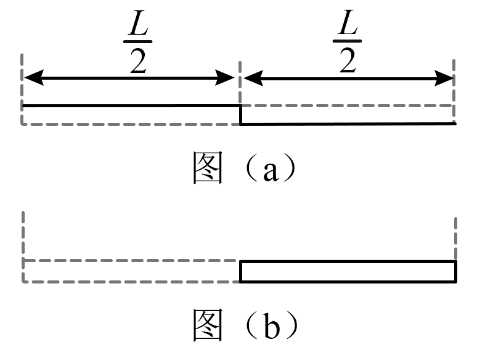．一个宽为 L 的双轨推拉门由两扇宽为 \(\frac{L}{2}\) 的门板组成。门处于关闭状态，其俯视图如图（a）所示。某同学用与门板平行的水平恒定拉力作用在一门板上，一段时间后撤去拉力，该门板完全运动到另一边，且恰好不与门框发生碰撞，其俯视图如图（b）所示。门板在运动过程中受到的阻力与其重力大小之比为 μ，重力加速度大小为 g。若要门板的整个运动过程用时尽量短，则所用时间趋近于（    ）

A．\(\sqrt {\frac{L}{{2\mu g}}} \)           B．\(\sqrt {\frac{L}{{\mu g}}} \)              C．\(\sqrt {\frac{2L}{{\mu g}}} \)             D．2\(\sqrt {\frac{L}{{\mu g}}} \)

【答案】

B

 

8．在如图所示的输电线路中，交流发电机的输出电压一定，两变压器均为理想变压器，左侧升压变压器的原、副线圈匝数分别为 n₁、n₂，两变压器间输电线路电阻为 r。下列说法正确的是（    ）

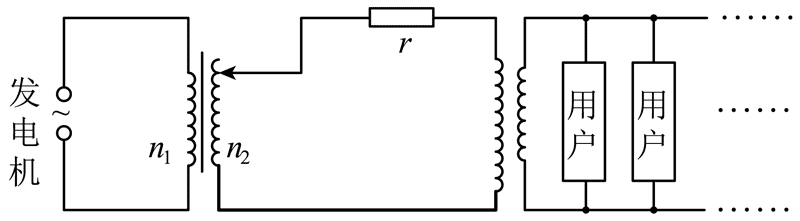
A．仅增加用户数，r 消耗的功率增大      B．仅增加用户数，用户端的电压增大

C．仅适当增加 n₂，用户端的电压增大     D．仅适当增加 n₂，整个电路消耗的电功率减小

【答案】

AC

 

9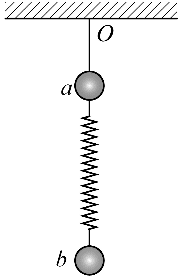．质量均为 m 的小球 a 和 b 由劲度系数为 k 的轻质弹簧连接，小球 a 由不可伸长的细线悬挂在 O 点，系统处于静止状态，如图所示。将小球 b 竖直下拉长度 l 后由静止释放。重力加速度大小为 g，忽略空气阻力，弹簧始终在弹性限度内。释放小球 b 后（    ）

A．小球 a 可能会运动

B．若小球 b 做简谐运动，则其振幅为 \(\frac{l}{2}\)

C．当且仅当 l ≤ \(\frac{{mg}}{k}\) 时，小球 b 才能始终做简谐运动

D．当且仅当 l ≤ \(\frac{{2mg}}{k}\) 时，小球 b 才能始终做简谐运动

【答案】

AD

【解析】

B．如果 A 球不动而 B 球单独振动则 B 球做简谐振动，简谐振动的平衡位置合力为零，即 B 球初始时刻位置，则可知 B 的振幅为 l，B 错误；

ACD．A 球发生运动的临界条件为弹簧对 A 球向上的弹力大于 A 球的重力，则此时对 A 球有 kx₀ = mg

对 B 球有此时加速度 kx₀ + mg = ma

由简谐振动的对称性可得向下拉到最低点松手释放的加速度也为 a，则有 kl = ma

解得 l = \(\frac{{2mg}}{k}\)

即 l ≤ \(\frac{{2mg}}{k}\)，否则 A 球会发生运动，AD 正确，C 错误。

故选 AD。

 

10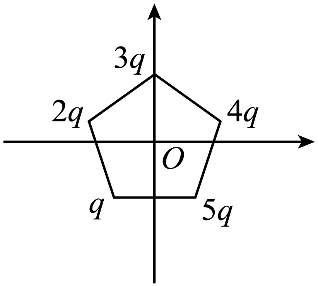．如图所示，在 xOy 平面内有一以 O 点为中心的正五边形，顶点到 O 点的距离为 R。在正五边形的顶点上顺时针方向依次固定电荷量为 q、2q、3q、4q、5q 的正点电荷，且电荷量为 3q 的电荷在 y 轴正半轴上。静电力常量为 k，则 O 点处的电场强度（    ）

A．方向沿 x 轴负方向

B．方向与 x 轴负方向成 18° 夹角斜向下

C．大小为 \(\frac{{2kq}}{{{R^2}}}\)(cos54° + cos18°)

D．大小为 \(\frac{{2kq}}{{{R^2}}}\)(2cos54° + cos18°)

【答案】

AD

【解析】

由题意可知，如图

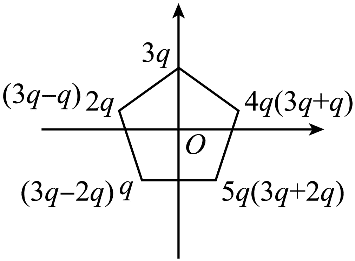
将五个点电荷等效成

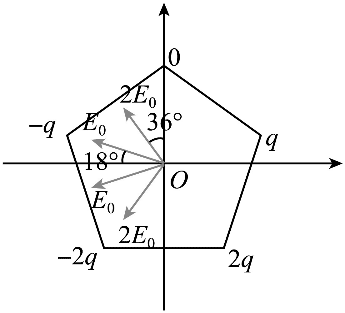
五个点电荷与 O 点距离为 R，设 E₀ = (\frac{{kq}}{{{R^2}}}\)

则 O 点场强大小为 E = 2×2E₀cos54° + 2E₀cos18°

代入可得 E = \(\frac{{2kq}}{{{R^2}}}\)(2cos54° + cos18°)

方向沿 x 轴负方向；

故选 AD。

 

11．某实验小组为测量一节干电池的电动势 E 和内阻 r，设计了如图（a）所示电路，所用器材如下：干电池、智能手机、电流传感器、定值电阻 R₀、电阻箱、开关、导线等。按电路图连接电路，将智能手机与电流传感器通过蓝牙无线连接，闭合开关 S，逐次改变电阻箱的阻值 R，用智能手机记录对应的电流传感器测得的电流 I。回答下列问题：

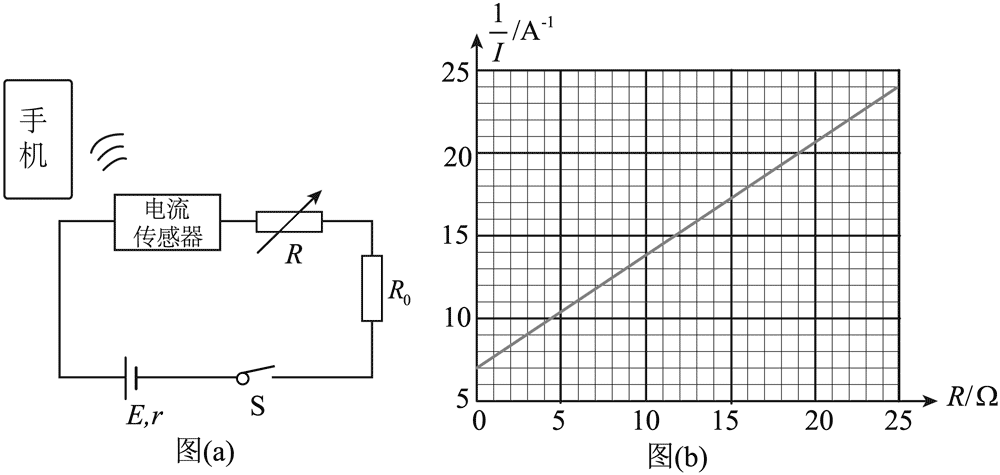
（1）R₀ 在电路中起______（填“保护”或“分流”）作用。

（2）\(\frac{1}{I}\) 与 E、r、R、R₀ 的关系式为\(\frac{1}{I}\) =______。

（3）根据记录数据作出 \(\frac{1}{I}\)–R 图像，如图（b）所示。已知 R₀ = 9.0 Ω，可得 E =______V（保留三位有效数字），r =______Ω（保留两位有效数字）

（4）电流传感器的电阻对本实验干电池内阻的测量结果______（填“有”或“无”）影响。

【答案】

（1）保护

（2）\(\frac{R}{E}\) + \(\frac{{{R_0} + r}}{E}\)

（3）1.47，1.3

（4）有

 

12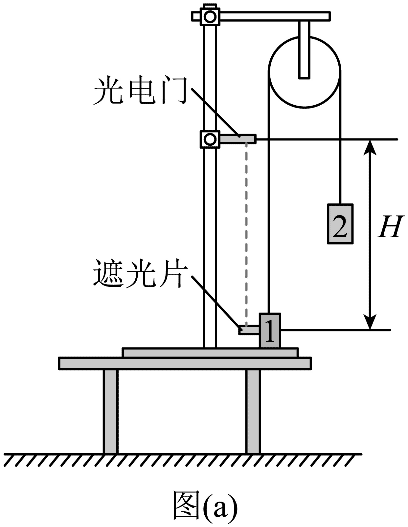．某同学利用如图（a）所示的实验装置来测量重力加速度大小 g。细绳跨过固定在铁架台上不可转动的小圆柱体，两端各悬挂一个重锤。实验步骤如下：

①用游标卡尺测量遮光片的宽度 d。

②将遮光片固定在重锤1上，用天平测量重锤 1 和遮光片的总质量 m、重锤 2 的质量 M（M > m）。

③将光电门安装在铁架台上，将重锤 1 压在桌面上，保持系统静止，重锤 2 离地面足够高。用刻度尺测量遮光片中心到光电门的竖直距离 H。

④启动光电门，释放重锤 1，用毫秒计测出遮光片经过光电门所用时间 t。

⑤根据上述数据求出重力加速度 g。

⑥多次改变光电门高度，重复步骤，求出 g 的平均值。

回答下列问题：

（1）测量 d 时，游标卡尺的示数如图（b）所示，可知______cm。

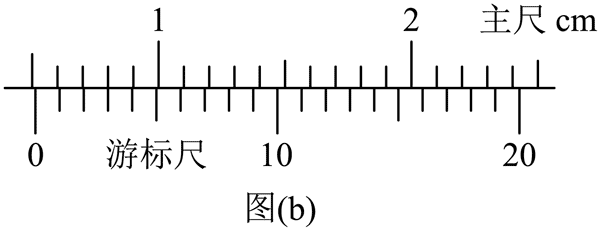
（2）重锤 1 通过光电门时的速度大小为 v =______（用遮光片 d、t 表示）。若不计摩擦，g 与 m、M、d、t、H 的关系式为______。

（3）实验发现，当 M 和 m 之比接近于 1 时，g 的测量值明显小于真实值。主要原因是圆柱体表面不光滑，导致跨过圆柱体的绳两端拉力不相等。理论分析表明，圆柱体与绳之间的动摩擦因数很小时，跨过圆柱体的绳两端拉力差 ΔT = 4γ \(\frac{{Mm}}{{M + m}}\)g，其中 γ 是只与圆柱体表面动摩擦因数有关的常数。保持 M + m = 2m₀ 不变，其中 M = (1 +β)m₀，m = (1 − β)m₀。β 足够小时，重锤运动的加速度大小可近似表示为 a = (β − γ)g。调整两重锤的质量，测得不同 β 时重锤的加速度大小 a，结果如下表。根据表格数据，采用逐差法得到重力加速度大小 g =______m/s²（保留三位有效数字）。

β	0.04	0.06	0.08	0.10
a/（m/s2）	0.084	0.281	0477	0.673

【答案】

（1）0.515

（2）\(\frac{d}{t}\)，\(\frac{{(M + m){d^2}}}{{2(M - m)H{t^2}}}\)

（3）9.81

【解析】

（1）根据游标卡尺的读数规律，该游标卡尺的读数为 5 mm + 0.05×3 mm = 5.15 mm = 0.515 cm。

（2）根据光电门的测速原理，重锤 1 通过光电门时的速度大小为 v = \(\frac{d}{t}\)。

对重锤 1 与重锤 2 构成的系统进行分析，根据系统机械能守恒定律有(M − m)gH = \(\frac{1}{2}\)(M + m)v²，其中 v = \(\frac{d}{t}\)。解得 g = \(\frac{{(M + m){d^2}}}{{2(M - m)H{t^2}}}\)。

（3）由于 γ 是只与圆柱体表面动摩擦因数有关的常数，且有a = (β − γ)g = βg –γg。取表格从左至右四组数据分别为a₁、a₂、a₃、a₄和对应的β₁、β₂、β₃、β₄，利用表格中的数据，根据逐差法有 a₄ + a₃ – a₂ – a₁ = (β₄ + β₃ – β₂ – β₁)g，带入数据可则重力加速度 g = 9.81 m/s²。

 

13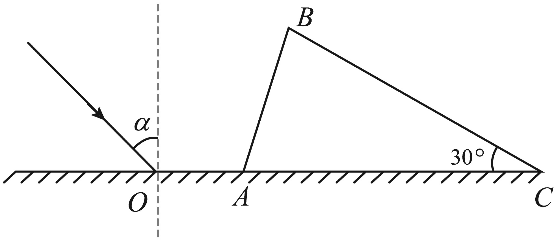．如图所示，三角形 ABC 是三棱镜的横截面，AC = BC，∠C = 30°，三棱镜放在平面镜上，AC 边紧贴镜面。在纸面内，一光线入射到镜面 O 点，入射角为 α，O 点离 A 点足够近。已知三棱镜的折射率为 \(\sqrt 2 \)。

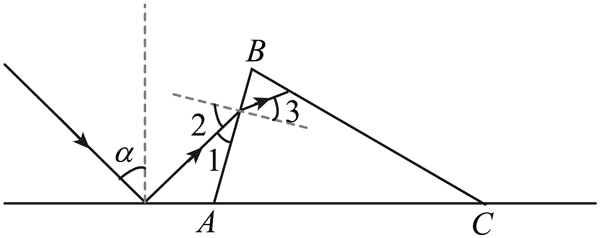
（1）当 α = 45° 时，求光线从 AB 边射入棱镜时折射角的正弦值；

（2）若光线从 AB 边折射后直接到达 BC 边，并在 BC 边刚好发生全反射，求此时的 α 值

【答案】

（1）\(\frac{{\sqrt 6 }}{4}\)

（2）60°

【解析】

 

14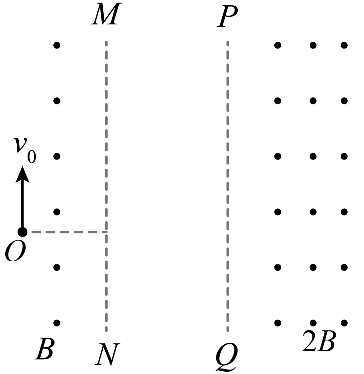．如图所示，两平行虚线 MN、PQ 间无磁场。MN 左侧区域和 PQ 右侧区域内均有垂直于纸面向外的匀强磁场，磁感应强度大小分别为 B 和 2B。一质量为 m、电荷量为 q 的带正电粒子从MN 左侧 O 点以大小为 v₀ 的初速度射出，方向平行于 MN 向上。已知 O 点到 MN 的距离为 \(\frac{{3m{v_0}}}{{2qB}}\)，粒子能回到 O 点，并在纸面内做周期性运动。不计重力，求：

（1）粒子在 MN 左侧区域中运动轨迹的半径；

（2）粒子第一次和第二次经过 PQ 时位置的间距；

（3）粒子的运动周期。

【答案】

（1）R = \(\frac{{m{v_0}}}{{qB}}\)

（2）x = \(\frac{{\sqrt 3 m{v_0}}}{{2qB}}\)

（3）\(\frac{{5\pi m}}{{3qB}}\) + \(\frac{{\sqrt 3 m}}{{qB}}\)

 

15．如图所示，一足够长的平直木板放置在水平地面上，木板上有 3n（n 是大于 1 的正整数）个质量均为 m 的相同小滑块，从左向右依次编号为 1、2、…、3n，木板的质量为 nm。相邻滑块间的距离均为 L，木板与地面之间的动摩擦因数为 μ，滑块与木板间的动摩擦因数为 2μ。初始时木板和所有滑块均处于静止状态。现给第 1 个滑块一个水平向右的初速度，大小为 \(\sqrt {\beta \mu gL} \)（β 为足够大常数，g 为重力加速度大小）。滑块间的每次碰撞时间极短，碰后滑块均会粘在一起继续运动。最大静摩擦力等于滑动摩擦力。

（1）求第 1 个滑块与第 2 个滑块碰撞前瞬间，第 1 个滑块的速度大小

（2）记木板滑动前第 j 个滑块开始滑动时的速度为 v_j，第 j + 1 个滑块开始滑动时的速度为 v_{j + 1}。用已知量和 v_j 表示 v_{j + 1}。

（3）若木板开始滑动后，滑块间恰好不再相碰，求 β 的值。（参考公式：1² + 2² + … + k² = \(\frac{1}{6}\)k(k + 1)(2k + 1)

【答案】

（1）v₁ = \(\sqrt {(\beta  - 4)\mu gL} \)

（2）v_{j + 1} = \(\frac{j}{{j + 1}}\sqrt {v_j^2 - 4\mu gL} \)

（3）β = \(\frac{{4n(2n + 1)(8{n^2} + 10n + 5)}}{{3(2n - 1)}}\)