1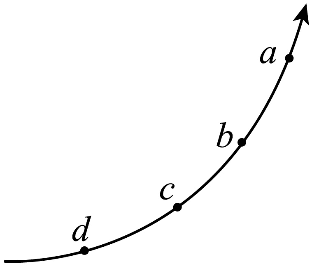．《汉书》记载“姑句家矛端生火”，表明古人很早就发现了尖端放电现象。若带电长矛尖端附近某条电场线如图，则 a、b、c、d 四点中电势最高的是（    ）

A．a 点          B．b 点          C．c 点           D．d 点

【答案】

D

【解析】

根据电场线的性质：沿电场线方向，电势逐渐降低。观察图中电场线，可判断电场线方向（假设从电势高处指向低处）。比较 a、b、c、d 四点，d 点位于电场线“上游”，沿电场线方向电势依次降低，即 d 点电势高于 c 点，c 点高于 b 点，b 点高于 a 点。因此电势最高的是 d 点。

故选 D。

 

2．某同学将一充气皮球遗忘在操场上，找到时发现因太阳曝晒皮球温度升高，体积变大。在此过程中若皮球未漏气，则皮球内封闭气体（    ）

A．对外做功                                          B．向外界传递热量

C．分子的数密度增大                         D．每个分子的速率都增大

【答案】

A

【解析】

A．皮球体积变大，气体膨胀，对外界做功，故 A 正确。

B．太阳暴晒使气体温度升高，是外界对气体传热（气体吸热），而非气体向外界传递热量，故 B 错误。

C．皮球未漏气，分子总数不变，体积变大，分子的数密度减小，故 C 错误。

D．温度升高，分子平均动能增大，但并非每个分子速率都增大，只是“平均”情况，故 D 错误。

故选 A。

 

3．1992 年，江苏扬州出土的古代铜卡尺，由固定尺和活动尺组成，现代游标卡尺的构件与其非常相似，已成为常用的测量工具。用游标卡尺测量某物体的长度，示数如图所示，其读数为（    ）

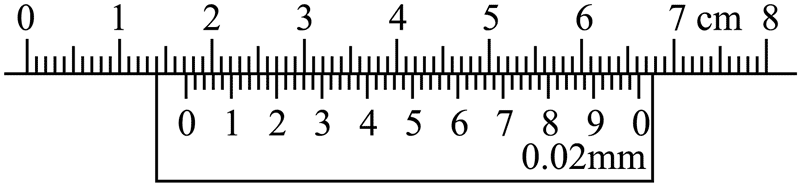
A．14.20 mm         B．14.2 mm           C．17.20 mm         D．17.2 mm

【答案】

C

【解析】

根据游标卡尺的读数规则可知主尺读数为 17 mm，游标尺为 50 分度，每分度值为 0.02 mm，第 10 条刻度线对齐，则游标尺的读数为 10×0.02 mm = 0.20 mm。

所以读数为 17 mm + 0.20 mm = 17.20 mm。

故选 C。

 

4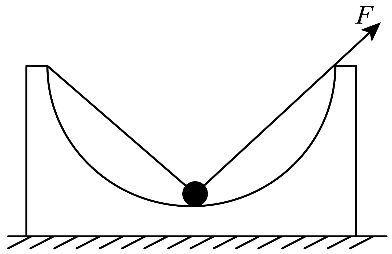．如图，内壁截面为半圆形的光滑凹槽固定在水平面上，左右边沿等高。该截面内，一根不可伸长的细绳穿过带有光滑孔的小球，一端固定于凹槽左边沿，另一端过右边沿并沿绳方向对其施加拉力 F。小球半径远小于凹槽半径，所受重力大小为 G。若小球始终位于内壁最低点，则 F 的最大值为（    ）

A．\(\frac{1}{2}\)G          B．\(\frac{{\sqrt 2 }}{2}\)G               C．G              D．\(\sqrt 2 \)G

【答案】

B

【解析】

分析可知当凹槽底部对小球支持力为零时，此时拉力 F 最大，根据平衡条件有 2F_mcos45° = G

解得 F_m = \(\frac{{\sqrt 2 }}{2}\)G

故选 B。

 

5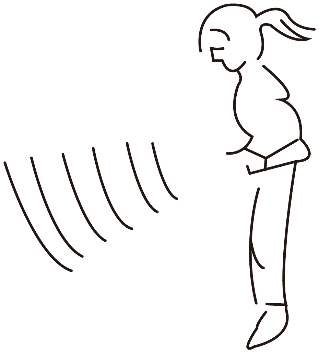．某同学在傍晚用内嵌多个彩灯的塑料绳跳绳，照片录了彩灯在曝光时间内的运动轨迹，简图如图。彩灯的运动可视为匀速圆周运动，相机本次曝光时间是 \(\frac{1}{2}\) s，圆弧对应的圆心角约为 30°，则该同学每分钟跳绳的圈数约为（    ）

A．90             B．120           C．150           D．180

【答案】

C

 

6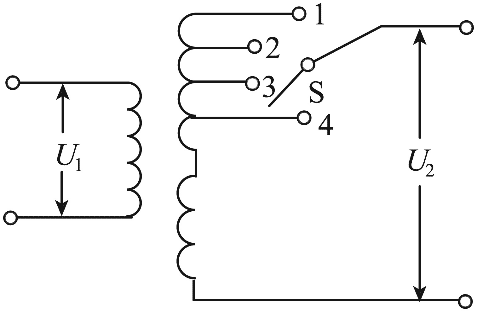．2024 年底，世界装机容量最大的抽水蓄能电站——河北丰宁抽水蓄能电站全面投产发电。如图，若该电站通过理想变压器调节输出电压 U₂ 时，输入电压 U₁ 保持不变。已知副线圈总匝数为 n，分接头 1、2 间和 2、3 间的线圈匝数 n₁₂ = n₂₃ = \(\frac{n}{{10}}\)，开关 S 接 3 时输出电压的瞬时值 u₂ = U_msinωt，则 S 接 2 时 u₂–t 的图像为（    ）

【答案】

D

 

7．随着我国航天事业飞速发展，人们畅想研制一种核聚变能源星际飞行器。从某星球表面发射的星际飞行器在飞行过程中只考虑该星球引力，不考虑自转，该星球可视为质量分布均匀的球体，半径为 R₀，表面重力加速度为 g₀。质量为 m 的飞行器与星球中心距离为 r 时，引力势能为 mg₀R₀²\(\left( {\frac{1}{{{R_0}}} - \frac{1}{r}} \right)\)（r ≥ R₀）。要使飞行器在距星球表面高度为 R₀ 的轨道上做匀速圆周运动，则发射初速度为（    ）

A．\(\sqrt {{g_0}{R_0}} \)             B．\(\sqrt {\frac{{3{g_0}{R_0}}}{2}} \)         C．\(\sqrt {2{g_0}{R_0}} \)           D．\(\sqrt {3{g_0}{R_0}} \)

【答案】

B

 

8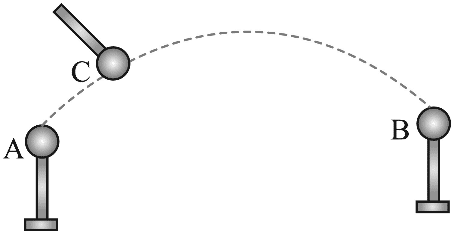．如图，真空中固定在绝缘台上的两个相同的金属小球 A 和 B，带有等量同种电荷，电荷量为 q，两者间距远大于小球直径，两者之间的静电力大小为 F。用一个电荷量为 Q 的同样的金属小球 C 先跟 A 接触，再跟 B 接触，移走 C 后，A 和 B 之间的静电力大小仍为 F，则 Q∶q 的绝对值可能是（    ）

A．1               B．2               C．3               D．5

【答案】

AD

 

9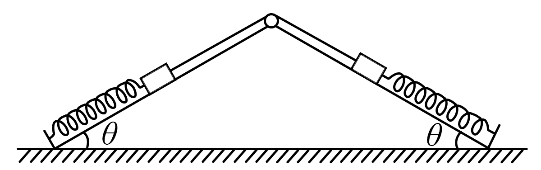．如图，截面为等腰三角形的光滑斜面体固定在水平地面上，两个相同的小物块通过不可伸长的细绳跨过顶端的轻质定滑轮，静止在斜面体两侧，细绳与斜面平行。此外，两物块分别用相同的轻质弹簧与斜面体底端相连，且弹簧均处于原长。将左侧小物块沿斜面缓慢拉下一小段距离，然后松开。弹簧始终在弹性限度内，斜面倾角为 θ，不计摩擦和空气阻力。在两物块运动过程中，下列说法正确的是（    ）

A．左侧小物块沿斜面做简谐运动

B．细绳的拉力随左侧小物块加速度的增大而增大

C．右侧小物块在最高位置的加速度与其在最低位置的加速度大小相等

D．若 θ 增大，则右侧小物块从最低位置运动到最高位置所用的时间变长

【答案】

AC

 

10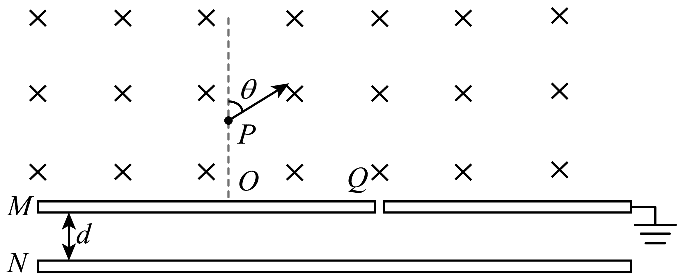．如图，真空中两个足够大的平行金属板 M、N 水平固定，间距为 d，M 板接地。M板上方整个区域存在垂直纸面向里的匀强磁场。M 板 O 点处正上方 P 点有一粒子源，可沿纸面内任意方向发射比荷、速度大小均相同的同种带电粒子。当发射方向与 OP 的夹角 θ = 60° 时，粒子恰好垂直穿过 M 板 Q 点处的小孔。已知 OQ = 3L，初始时两板均不带电，粒子碰到金属板后立即被吸收，电荷在金属板上均匀分布，金属板电量可视为连续变化，不计金属板厚度、粒子重力及粒子间的相互作用，忽略边缘效应。下列说法正确的是（    ）

A．粒子一定带正电

B．若间距 d 增大，则板间所形成的最大电场强度减小

C．粒子打到 M 板上表面的位置与 O 点的最大距离为 7L

D．粒子打到 M 板下表面的位置与 Q 点的最小距离为 \(\sqrt 3 \)d

【答案】

BCD

 

11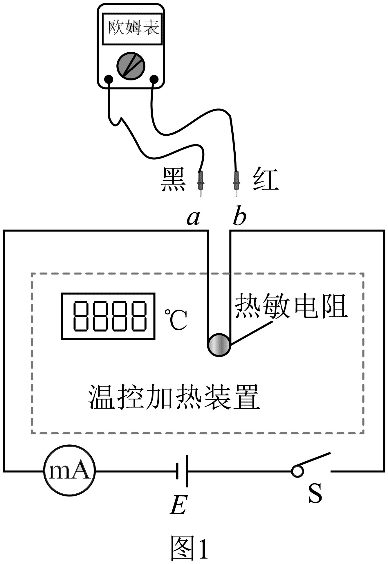．某学习小组把热敏电阻置于带有温控的加热装置中，利用图 1 所示电路研究热敏电阻的温度特性。

（1）闭合开关 S，观察到温度改变时电流表示数也随之改变。定量研究热敏电阻的阻值 R 随温度 t 变化的规律时，将欧姆表两表笔分别接到热敏电阻 a、b 两端测量其阻值，这时开关 S 应________（填“断开”或“闭合”）。

（2）按照正确方法测出不同温度下热敏电阻的阻值。电阻 R₁、R₂ 与温度t的关系分别对应图 2 中曲线 Ⅰ、Ⅱ。设计电路时，为防止用电器发生故障引起电流异常增大，导致个别电子元件温度过高而损坏，可串联一个热敏电阻抑制电流异常增大，起到过热保护作用。这种热敏电阻与电阻________（填“R₁”或“R₂”）具有相同温度特性。

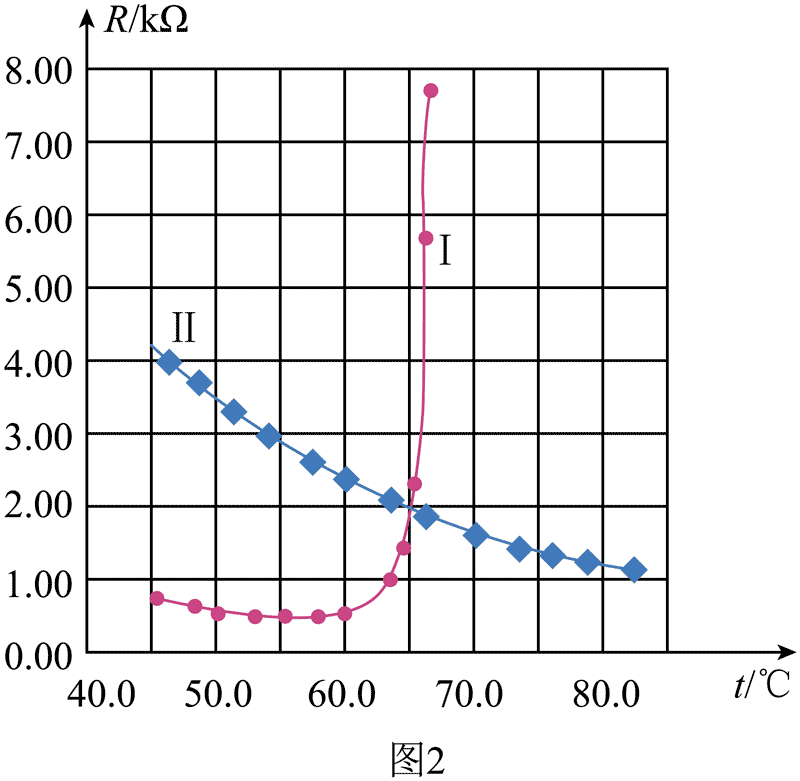
【答案】

（1）断开

（2）R₁

 

11．某学习小组在倾斜的气垫导轨上验证机械能守恒定律，实验装置如图 3 所示，当地重力加速度为 g。

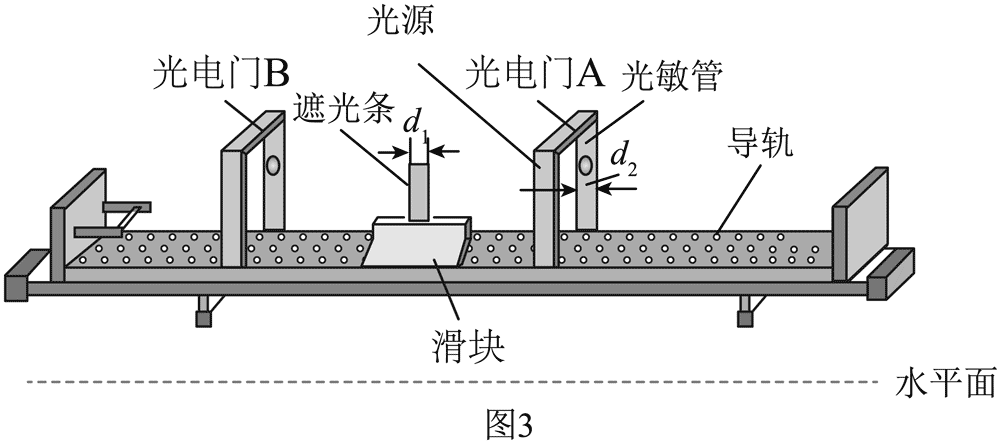
（1）方案设计阶段，该小组同学对需要测量哪些物理量产生了不同意见。

甲同学：需测量滑块和遮光条的总质量、滑块通过两个光电门的速度、两个光电门间的竖直高度差。

乙同学：只需测量滑块通过两个光电门的速度、两个光电门间的竖直高度差。

丙同学：只需测量滑块通过两个光电门的速度、两个光电门间的距离。

你认为________（填“甲”“乙”或“丙”）同学的方案不可行。

（2）如图 3，光电门中光源与光敏管相对，光源发出的光使光敏管感光。当滑块经过时，遮光条把光遮住，计时器记录遮光时间，可计算出滑块的速度。实验中使用的遮光条宽度 d₁ = 10.0 mm，光电门宽度 d₂ = 20.0 mm。某次测量时，记录通过光电门 A 的遮光时间为 25.0 ms，则滑块经过光电门 A 的速度大小为________m/s。

【答案】

（1）丙

（2）0.4

 

12．自动洗衣机水位检测的精度会影响洗净比和能效等级。某款洗衣机水位检测结构如图 1 所示。洗衣桶内水位升高时，集气室内气体压强增大，铁芯进入电感线圈的长度增加，从而改变线圈的自感系数。洗衣机智能电路通过测定 LC 振荡电路的频率来确定水位高度。

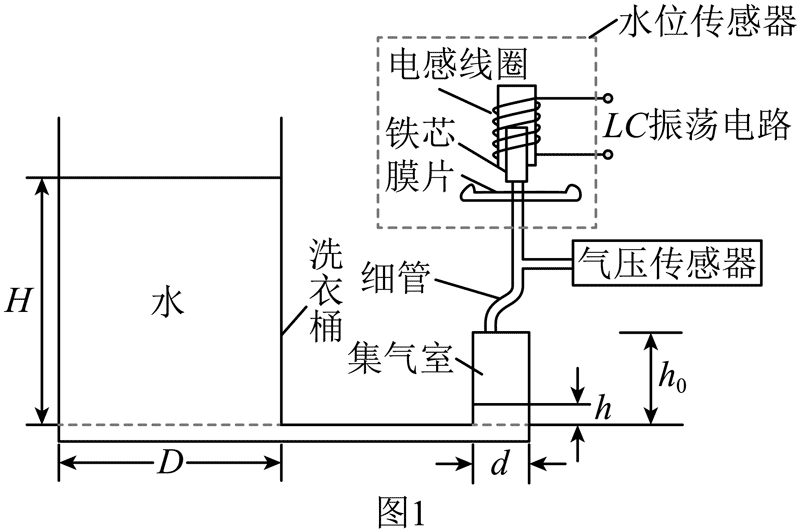
某兴趣小组在恒温环境中对此装置进行实验研究。

（1）研究集气室内气体压强与体积的关系

①洗衣桶内水位 H 一定时，其内径 D 的大小________（填“会”或“不会”）影响集气室内气体压强的大小。

②测量集气室高度 h₀、集气室内径 d。然后缓慢增加桶内水量，记录桶内水位高度 H 和集气室进水高度，同时使用气压传感器测量集气室内气体压强 p。H 和 h 数据如下表所示。

H/cm	15.00	20.00	25.00	30.00	35.00	40.00	45.00	50.00
h/cm	0.33	0.40	0.42	0.52	0.61	0.70	078	0.87

实验中使用同一把刻度尺对 H 和 h 进行测量，根据数据判断，测量________（填“H”或“h”）产生的相对误差较小。

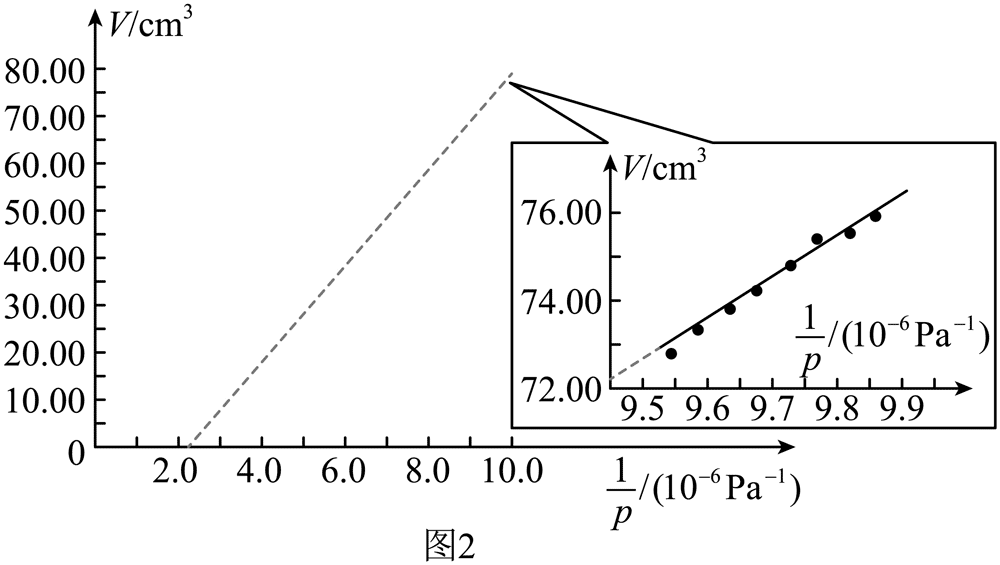
③利用数据处理软件拟合集气室内气体体积 V 与 \(\frac{1}{p}\) 的关系曲线，如图 2 所示。图中拟合直线的延长线明显不过原点，经检查实验仪器完好，实验装置密封良好，操作过程规范，数据记录准确，则该延长线不过原点的主要原因是_____________________________________。

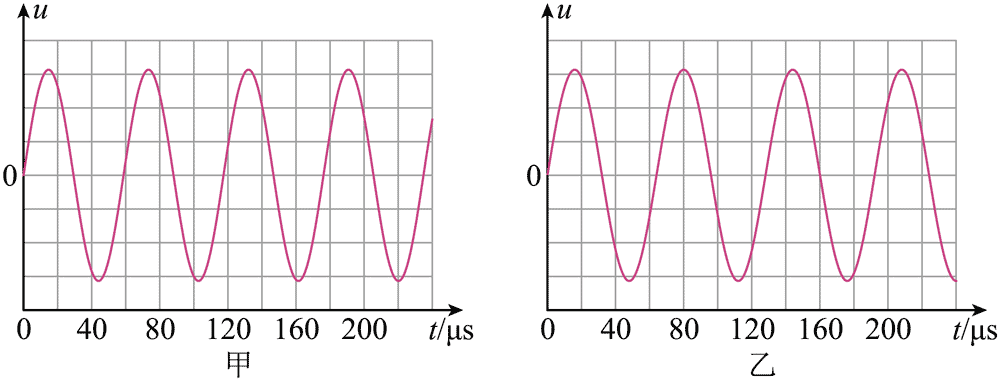
（2）研究洗衣桶水位高度与振荡电路频率的关系图 3 是桶内水位在两个不同高度时示波器显示的 u–t 图像，u 的频率即为 LC 振荡电路的频率。LC 振荡电路的频率 f 与线圈自感系数 L、电容 C 的关系是 f = \(\frac{1}{{2\pi \sqrt {LC} }}\)，则图中________（填“甲”或“乙”）对应的水位较高。

【答案】

（1）①不会          ②H

③该延长线不过原点的主要原因是与集气室相连的细管中的气体被忽略不计，导致集气室气体体积 V 相比于实际气体体积偏小。

（2）乙

【解析】

（1）①集气室内气体压强等于桶内水位高度 H 和集气室进水高度的高度差产生的压强和大气压强之和，根据 p = ρgh 可知其内径 D 的大小不会影响影响集气室内气体压强的大小；

②由于实验中使用同一把刻度尺进行测量，分度值相同，根据数据分析，桶内水位高度 H 明显大于集气室内进水高度 h，所以测量桶内水位高度 H 产生的相对误差较小；

③该延长线不过原点的主要原因是与集气室相连的细管中的气体被忽略不计，导致集气室气体体积 V 相比于实际气体体积偏小。

（2）桶内水位高度 H 越大，集气室内气体压强越大，铁芯进入电感线圈的长度越大，电感线圈的自感系数越大，根据 T = 2π\({\sqrt {LC} }\) 可知 LC 振荡电路的周期越大，所以图 3 中乙对应的水位较高。

 

13．光纤光谱仪的部分工作原理如图所示。待测光在光纤内经多次全反射从另一端射出，再经棱镜偏转，然后通过狭缝进入光电探测器。

（1）若将光纤简化为真空中的长玻璃丝，设玻璃丝的折射率为 \(\frac{{2\sqrt 3 }}{3}\)，求光在玻璃丝内发生全反射时的最小入射角。

（2）若探测器光阴极材料的逸出功为9.939×10⁻²⁰ J，求该材料的截止频率。（普朗克常量h = 6.626×10⁻³⁴ J·s）

【答案】

（1）60°

（2）1.5×10¹⁴ Hz

【解析】

（1）光在玻璃丝内发生全反射的最小入射角满足 sinC = \(\frac{1}{n}\)

可得 C = 60°

（2）根据爱因斯坦光电方程 hν₀ = W₀

可得 ν₀ = 1.5×10¹⁴ Hz

 

14．如图，一长为 2 m 的平台，距水平地面高度为 1.8 m。质量为 0.01 kg 的小物块以 3 m/s 的初速度从平台左端水平向右运动。物块与平台、地面间的动摩擦因数均为 0.2。物块视为质点，不考虑空气阻力，重力加速度 g 取 10 m/s²。

（1）求物块第一次落到地面时距平台右端的水平距离。

（2）若物块第一次落到地面后弹起的最大高度为 0.45 m，物块从离开平台到弹起至最大高度所用时间共计 1 s。求物块第一次与地面接触过程中，所受弹力冲量的大小，以及物块弹离地面时水平速度的大小。

【答案】

（1）0.6 m

（2）I_N = 0.1 N·s；v_xʹ = 0

【解析】

（1）小物块在平台做匀减速直线运动，根据牛顿第二定律有 a = μg

则小物块从开始运动到离开平台有 v_x² – v₀² = 2ax₀

小物块从平台飞出后做平抛运动有 h = \(\frac{1}{2}\)gt₁²，x = v_xt₁

联立解得 x = 0.6 m

（2）物块第一次落到地面后弹起的最大高度为 0.45 m，则物块弹起至最大高度所用时间和弹起的初速度有 hʹ = \(\frac{1}{2}\)gt₂²，v_y2 = gt₂

则物块与地面接触的时间 Δt = t − t₁ − t₂ = 0.1 s

物块与地面接触的过程中根据动量定理，取竖直向上为正，在竖直方向有 I_N − mgΔt = mv_y2 − m(− v_y1)，v_y1 = gt₁

解得 I_N = 0.1N·s

取水平向右为正，在水平方向有 − μNΔt = mv_xʹ − mv_x，I = NΔt

解得 v_xʹ = − 1 m/s

但由于 v_xʹ 减小为0将无相对运动和相对运动的趋势，故 v_xʹ = 0

 

15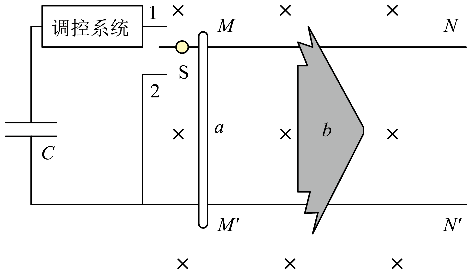．某电磁助推装置设计如图，超级电容器经调控系统为电路提供 1 000 A 的恒定电流，水平固定的平行长直导轨处于垂直水平面的匀强磁场中，a 可视为始终垂直导轨的导体棒，b 为表面绝缘的无人机。初始时 a 静止于 MM′ 处，b 静止于 a 右侧某处。现将开关 S 接 1 端，a 与 b 正碰后锁定并一起运动，损失动能全部储存为弹性势能。当 a 运行至 NN′ 时将 S 接 2 端，同时解除锁定，所储势能瞬间全部转化为动能，a 与 b 分离。已知电容器电容 C 为 10 F，导轨间距为 0.5 m，磁感应强度大小为 1 T，MM′ 到 NN′ 的距离为 5 m，a、b 质量分别为 2 kg、8 kg，a 在导轨间的电阻为 0.01 Ω。碰撞、分离时间极短，各部分始终接触良好，不计导轨电阻、摩擦和储能耗损，忽略电流对磁场的影响。

（1）若分离后某时刻 a 的速度大小为 10 m/s，求此时通过 a 的电流大小。

（2）忽略 a、b 所受空气阻力，当 a 与 b 的初始间距为 1.25 m 时，求 b 分离后的速度大小，分析其是否为 b 能够获得的最大速度；并求 a 运动过程中电容器的电压减小量。

（3）忽略 a 所受空气阻力，若 b 所受空气阻力大小与其速度 v 的关系为 f = kv²（k = 0.025 N·s²/m²），初始位置与（2）问一致，试估算 a 运行至 NN′ 时。a 分离前的速度大小能否达到（2）问中分离前速度的 99%，并给出结论。（0.99² = 0.980 1）

【答案】

（1）500 A

（2）v_b1 = 25 m/s，能，ΔU = 40 V

（3）能