3．一列简谐横波在均匀介质中沿 x 轴传播，图 1 是 t = 1 s 时该波的波形图，图 2 是 x = 0 处质点的振动图像。则 t = 11 s 时该波的波形图为（    ）

【答案】

C

 

4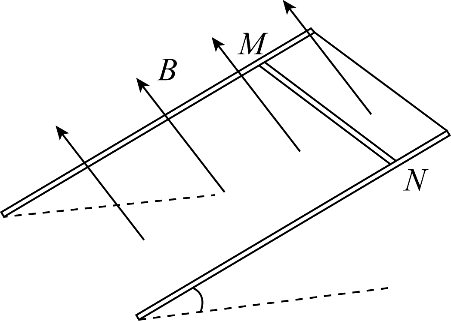．如图所示，两根不计电阻的光滑金属导轨平行放置，导轨及其构成的平面均与水平面成某一角度，导轨上端用直导线连接，整个装置处在垂直于导轨平面向上的匀强磁场中。具有一定阻值的金属棒 MN 从某高度由静止开始下滑，下滑过程中 MN 始终与导轨垂直并接触良好，则 MN 所受的安培力 F 及其加速度 a、速度 v、电流 I，随时间 t 变化的关系图像可能正确的是（    ）

【答案】

A

 

6．中国钍基熔盐堆即将建成小型实验堆，为我国能源安全和可持续发展提供有力支持。反应堆中涉及的核反应方程有：①X + ²³²₉₀Th → ²³³₉₀Th②²³³₉₀Th → ²³³₉₁Pa + ⁰₋₁e，下列说法正确的是（    ）

A．方程①中 X 是中子

B．方程②中 ²³³₉₀Th 发生了 β 衰变

C．受反应堆高温影响，²³³₉₀Th 的半衰期会变短

D．方程②释放电子，说明电子是原子核的组成部分

【答案】

AB

【解析】

A．根据核反应的质量数和电荷数守恒可知，方程①中 X 质量数为 1，电荷数为零，则是中子，选项 A 正确；

B．方程②中 ²³³₉₀Th 放出负电子，则发生了 β 衰变，选项 B 正确；

C．放射性元素的半衰期与外界因素无关，选项 C 错误；

D．方程②释放的电子是原子核内的中子转化为质子时放出的，不能说明电子是原子核的组成部分，选项 D 错误。

故选 AB。

 

7．卫星未发射时静置在赤道上随地球转动，地球半径为 R。卫星发射后在地球同步轨道上做匀速圆周运动，轨道半径为 r。则卫星未发射时和在轨道上运行时（    ）

A．角速度之比为 1∶1                        B．线速度之比为 \(\sqrt r \)∶\(\sqrt R \)

C．向心加速度之比为 R∶r                D．受到地球的万有引力之比为 R²∶r²

【答案】

AC

【解析】

A．卫星未发射时静置在赤道上随地球转动，角速度与地球自转角速度相等，卫星发射后在地球同步轨道上做匀速圆周运动，角速度与地球自转角速度相等，则卫星未发射时和在轨道上运行时角速度之比为 1∶1，故 A 正确；

B．根据题意，由公式 v = ωr 可知，卫星未发射时和在轨道上运行时，由于角速度相等，则线速度之比为轨道半径之比 R∶r，故 B 错误；

C．根据题意，由公式 a_n = ω²r 可知，卫星未发射时和在轨道上运行时，由于角速度相等，则向心加速度之比为轨道半径之比 R∶r，故 C 正确；

D．根据题意，由万有引力定律可知，卫星未发射时和在轨道上运行时，受到地球的万有引力之比与轨道半径的平方成反比，即 r²∶R²，故 D 错误。

故选 AC。

 

8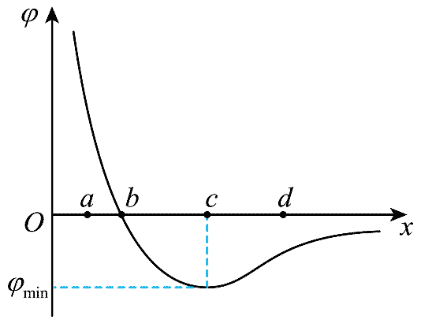．某静电场在 x 轴正半轴的电势 φ 随 x 变化的图像如图所示，a、b、c、d 为 x 轴上四个点。一负电荷仅在静电力作用下，以一定初速度从 d 点开始沿 x 轴负方向运动到 a 点，则该电荷（    ）

A．在 b 点电势能最小

B．在 c 点时速度最小

C．所受静电力始终做负功

D．在 a 点受静电力沿 x 轴负方向

【答案】

BD

【解析】

AB．根据题意，由公式 E_p = qφ 可知，负电荷在高电势位置的电势能较小，由图可知，a 点的电势最大，则在 a 点电势能最小，同理可知，c 点的电势最小，则在 c 点时电势能最大，电荷仅在电场力作用下，电荷的电势能和动能之和不变，可知，电势能最大时，动能最小，则在 c 点时，电荷的动能最小，即速度最小，故 A 错误，B 正确；

CD．根据沿电场线方向电势逐渐降低，结合题图可知，c 点左侧电场方向沿 x 轴正方向，c 点右侧电场方向沿 x 轴负方向，可知，c 点右侧负电荷受沿 x 轴正方向的电场力，c 点左侧负电荷受沿 x 轴负方向的电场力，可知，在 a 点受静电力沿 x 轴负方向，从 d 点开始沿 x 轴负方向运动到 a 点，电场力先做负功再做正功，故 C 错误，D 正确。

故选 BD。

 

9．某同学研究闭合电路的规律。

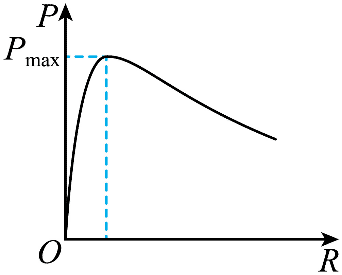（1）根据闭合电路的欧姆定律得出了电源输出功率 P 与外电路电阻关系图像，如图所示，则 P 的峰值对应的外电路电阻值 R 应_________电源内阻 r（填“大于”、“小于”或“等于”）；

（2）测定电源的电动势和内阻，可供选用的器材有：

A．电压表：（量程 0 ~ 3 V，内阻约为 3 kΩ）

B．电流表：（量程 0 ~ 0.6 A，内阻约为 1 Ω）

C．滑动变阻器：（最大阻值 20 Ω，额定电流 1 A）

D．滑动变阻器：（最大阻值 1000 Ω，额定电流 0.5 A）

E．待测电源：（电动势约为 3 V，内阻约为 1 Ω）

F．开关、导线若干

（i）实验中所用的滑动变阻器应选_________（填器材前字母代号）；

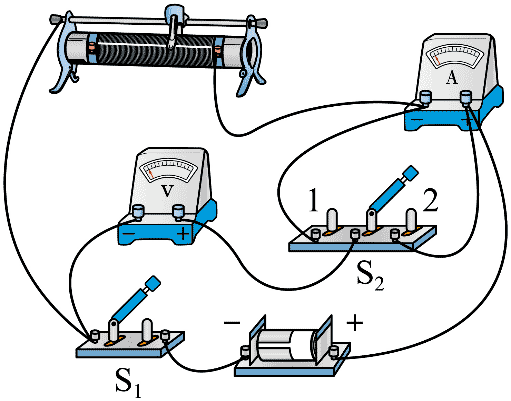
（ii）实物电路如图所示，单刀双掷开关 S₂ 可分别与 1、2 端闭合，为使电源内阻的测量结果更接近真实值，S₂ 应与_________端闭合。

【答案】

（1）等于

（2）C，2

 

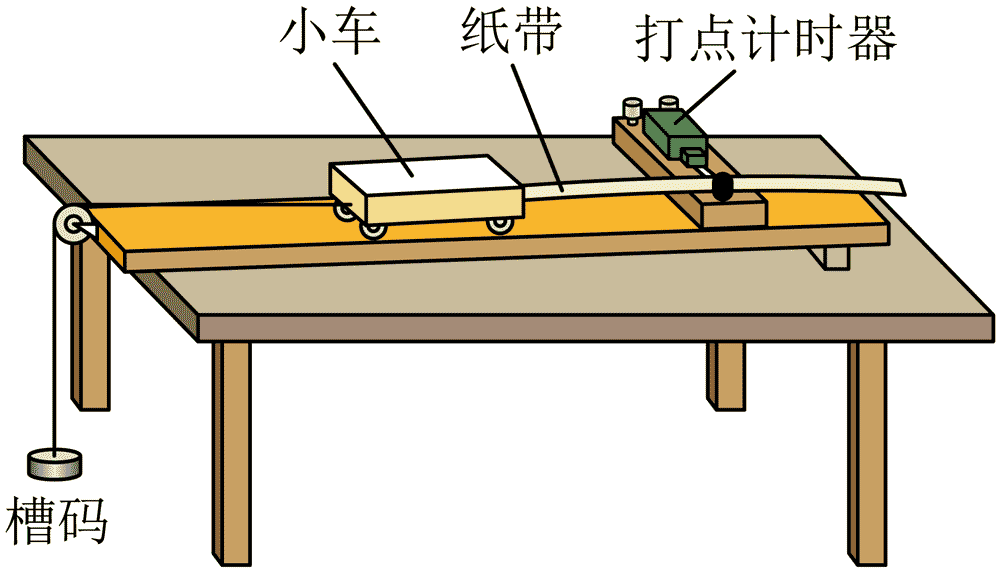
9．9．某同学用图示装置探究加速度与力的关系。

（1）为补偿打点计时器对小车的阻力及其他阻力，调节木板倾角，使小车在不挂槽码时运动，并打出纸带进行检验，下图中能表明补偿阻力恰当的是_________；

（2）某次实验得到一条纸带，部分计数点如下图所示（每相邻两个计数点间还有 4 个点，图中未画出），测得 s₁ = 6.20 cm，s₂ = 6.70 cm，s₃ = 7.21 cm，s₄ = 7.73 cm。已知打点计时器所接交流电源频率为 50 Hz，则小车的加速度 a = _________m/s²（要求充分利用测量数据，结果保留两位有效数字）；

（3）该同学将一个可以直接测出绳子拉力的传感器安装在小车上，小车和传感器总质量为 210 g。按要求补偿阻力后，该同学共进行了四次实验，悬挂的槽码质量依次为 5 g、10 g、20 g、40 g。处理数据时，用两种方式得到小车（含传感器）受到的合力，一种将槽码所受重力当作合力、另一种将传感器示数当作合力，则这两种方式得到的合力差异最大时，槽码质量为_______g。

【答案】

（1）B

（2）0.51

（3）40

 

10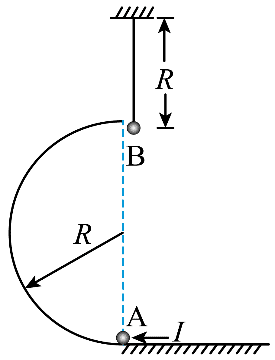．如图所示，光滑半圆轨道直径沿竖直方向，最低点与水平面相切。对静置于轨道最低点的小球 A 施加水平向左的瞬时冲量 I，A 沿轨道运动到最高点时，与用轻绳悬挂的静止小球 B 正碰并粘在一起。已知 I = 1.8 N∙s，A、B的质量分别为 m_A = 0.3 kg、m_B = 0.1 kg，轨道半径和绳长均为 R = 0.5 m，两球均视为质点，轻绳不可伸长，重力加速度 g 取 10 m/s²，不计空气阻力。求：

（1）与 B 碰前瞬间 A 的速度大小；

（2）A、B 碰后瞬间轻绳的拉力大小。

【答案】

（1）4 m/s

（2）11.2 N

 

11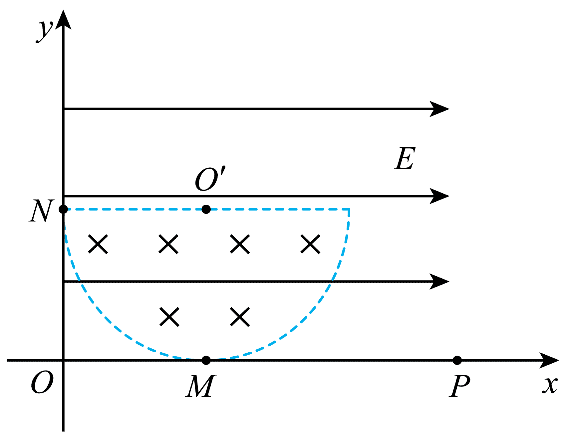．如图所示，在 Oxy 平面直角坐标系的第一象限内，存在半径为 R 的半圆形匀强磁场区域，半圆与 x 轴相切于 M 点，与 y 轴相切于 N 点，直线边界与 x 轴平行，磁场方向垂直于纸面向里。在第一象限存在沿 + x 方向的匀强电场，电场强度大小为 E。一带负电粒子质量为 m，电荷量为 q，从 M 点以速度 v 沿 + y 方向进入第一象限，正好能沿直线匀速穿过半圆区域。不计粒子重力。

（1）求磁感应强度 B 的大小；

（2）若仅有电场，求粒子从 M 点到达 y 轴的时间 t；

（3）若仅有磁场，改变粒子入射速度的大小，粒子能够到达 x 轴上 P 点，M、P 的距离为 \(\sqrt 3 \)R，求粒子在磁场中运动的时间 t₁。

【答案】

（1）B = \(\frac{E}{v}\)

（2）t = \(\sqrt {\frac{{2mR}}{{qE}}} \)

（3）t₁ = \(\frac{{2\pi mv}}{{3qE}}\)

【解析】

 

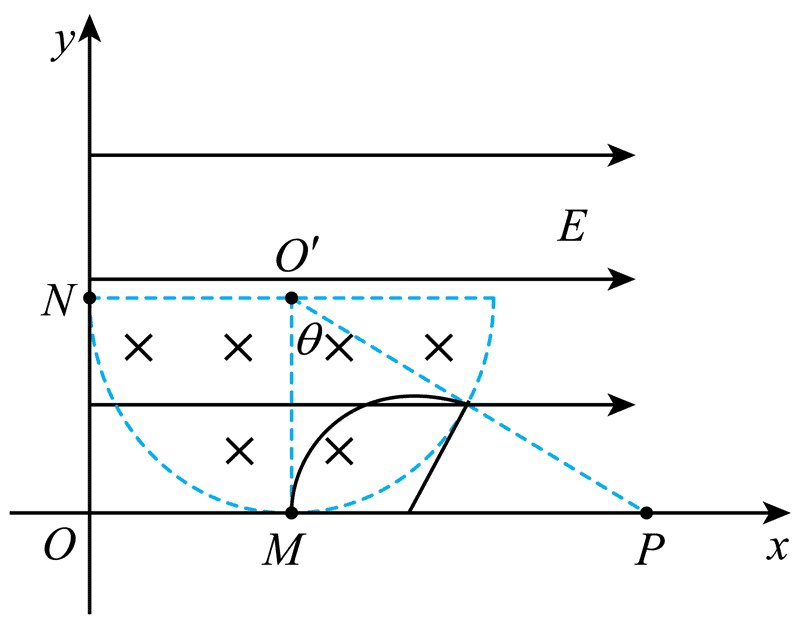
12．电动汽车制动过程中可以控制电机转为发电模式，在产生制动效果的同时，将汽车的部分机械能转换为电能，储存在储能装置中，实现能量回收、降低能耗。如图 1 所示，发电机可简化为处于匀强磁场中的单匝正方形线框 ABCD，线框边长为 L，电阻忽略不计，磁场磁感应强度大小为 B，线框转轴 OOʹ 与磁场垂直，且与 AB、CD 距离相等。线框与储能装置连接。

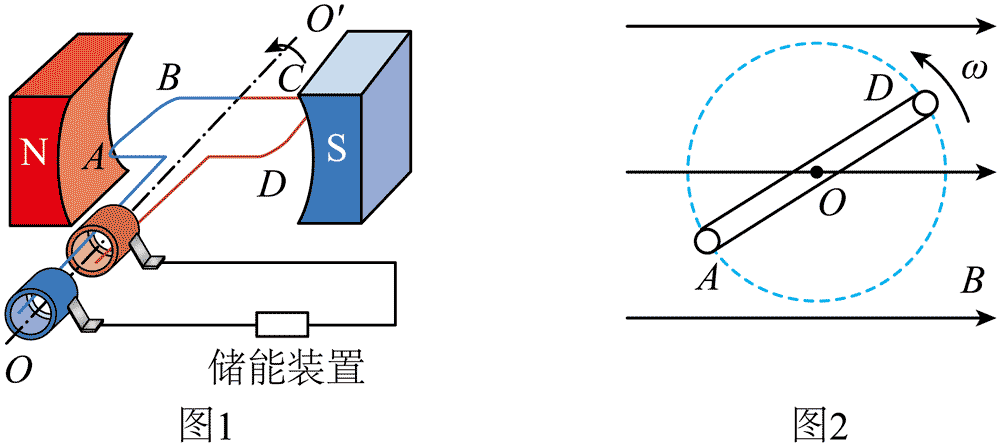
（1）线框转动方向如图 1 所示，试判断图示位置 AB 中的电流方向；

（2）若线框以角速度 ω 匀速转动，线框平面与中性面垂直瞬间开始计时，线框在 t 时刻位置如图 2 所示，求此时 AB 产生的感应电动势；

（3）讨论电动汽车在某次制动储存电能时，为方便计算，做两点假定：①将储能装置替换为阻值为 R 的电阻，电阻消耗的电能等于储能装置储存的电能；②线框转动第一周的角速度为 ω₀，第二周的角速度为 \(\frac{{{\omega _0}}}{2}\)，第三周的角速度为 \(\frac{{{\omega _0}}}{4}\)，依次减半，直到线框停止转动。若该制动过程中汽车在水平路面上做匀减速直线运动，汽车质量为 m，加速度大小为 a，储存的电能为初动能的 50%，求制动过程中汽车行驶的最大距离 x。

【答案】

（1）电流方向从 B 到 A

（2）e = \(\frac{1}{2}\)ωBL²cosωt

（3）x = \(\frac{{4\pi {\omega _0}{B^2}{L^4}}}{{maR}}\)