1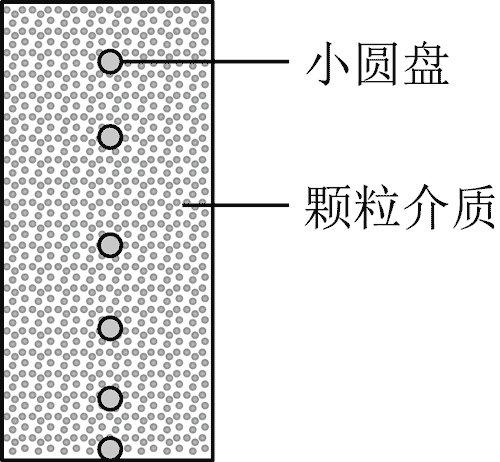．某研究人员将一铁质小圆盘放入聚苯乙烯颗粒介质中，在下落的某段时间内，小圆盘仅受重力 G 和颗粒介质对其向上的作用力 f。用高速相机记录小圆盘在不同时刻的位置，相邻位置的时间间隔相等，如图所示，则该段时间内下列说法可能正确的是（    ）

A．f 一直大于 G                                   B．f 一直小于 G

C．f 先小于 G，后大于 G                 D．f 先大于 G，后小于 G

【答案】

C

【解析】

由图可知相等时间内铁质小圆盘的位移先增大后减小，可知铁质小圆盘先加速后减速，即加速度先向下后向上。根据牛顿第二定律可知 f 先小于 G，后大于 G。

故选 C。

 

2．土星的部分卫星绕土星的运动可视为匀速圆周运动，其中的两颗卫星轨道半径分别为 r₁、r₂ 且 r₁ ≠ r₂，向心加速度大小分别为 a₁、a₂，则（    ）

A．\(\frac{{{a_1}}}{{{r_1}}}\) = \(\frac{{{a_2}}}{{{r_2}}}\)                  B．\(\frac{{{a_1}}}{{r_1^2}}\) = \(\frac{{{a_2}}}{{r_2^2}}\)                 C．a₁r₁ = a₂r₂                 D．a₁r₁² = a₂r₂²

【答案】

D

 

3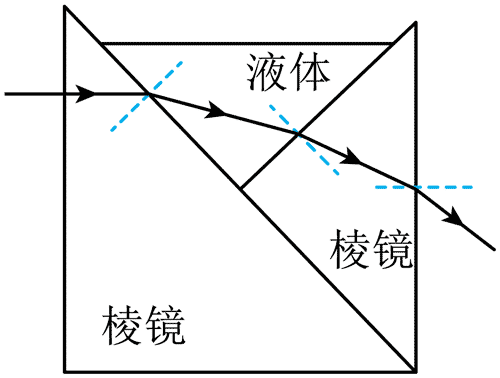．一种测量液体折射率的 V 形容器，由两块材质相同的直角棱镜粘合，并封闭其前后两端制作而成。容器中盛有某种液体，一激光束从左边棱镜水平射入，通过液体后从右边棱镜射出，其光路如图所示。设棱镜和液体的折射率分别为 n₀、n，光在棱镜和液体中的传播速度分别为 v₀、v，则（    ）

A．n < n₀，v >v₀                  B．n < n₀，v < v₀

C．n > n₀，v >v₀                   D．n > n₀，v < v₀

【答案】

A

 

4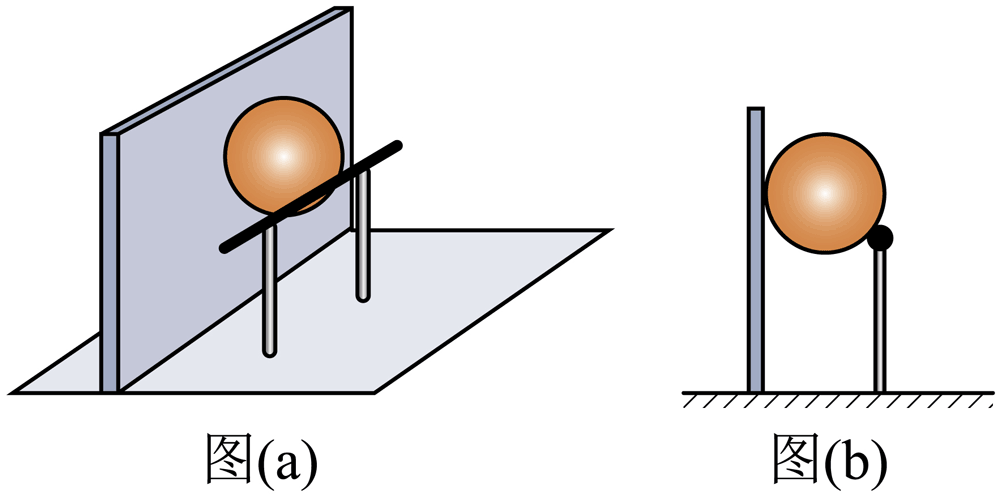．如图（a），一质量为 m 的匀质球置于固定钢质支架的水平横杆和竖直墙之间，并处于静止状态，其中一个视图如图（b）所示。测得球与横杆接触点到墙面的距离为球半径的 1.8 倍，已知重力加速度大小为 g，不计所有摩擦，则球对横杆的压力大小为（    ）

A．\(\frac{3}{5}\)mg                 B．\(\frac{3}{4}\)mg                 C．\(\frac{4}{3}\)mg                 D．\(\frac{5}{3}\)mg

【答案】

D

 

5．如图，两根相互平行的长直导线与一“凸”形导线框固定在同一竖直平面内，导线框的对称轴与两长直导线间的距离相等。已知左、右两长直导线中分别通有方向相反的恒定电流 I₁、I₂，且 I₁ > I₂，则当导线框中通有顺时针方向的电流时，导线框所受安培力的合力方向（    ）

A．竖直向上                          B．竖直向下

C．水平向左                          D．水平向右

【答案】

C

【解析】

根据右手螺旋定则可知导线框所在磁场方向向里，由于 I₁ > I₂，可知左侧的磁场强度大，同一竖直方向上的磁场强度相等，故导线框水平方向导线所受的安培力相互抵消，根据左手定则结合 F = BIL 可知左半边竖直方向的导线所受的水平向左的安培力大于右半边竖直方向的导线所受的水平向右的安培力，故导线框所受安培力的合力方向水平向左。

故选 C。

 

6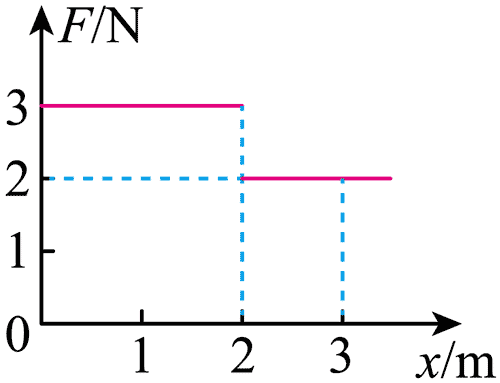．质量为 1 kg 的物块静置于光滑水平地面上，设物块静止时的位置为 x 轴零点。现给物块施加一沿 x 轴正方向的水平力 F，其大小随位置 x 变化的关系如图所示，则物块运动到 x = 3 m 处，F 做功的瞬时功率为（    ）

A．8 W           B．16 W         C．24 W         D．36 W

【答案】

A

【解析】

根据图像可知物块运动到 x = 3 m 处，F 做的总功为 W_F = （3×2 + 2×1）J = 8 J

该过程根据动能定理得 W_F = \(\frac{1}{2}\)mv²

解得物块运动到 x = 3 m 处时的速度为 v = 4 m/s

故此时F做功的瞬时功率为 P = Fv = 8 W

故选 A。

 

7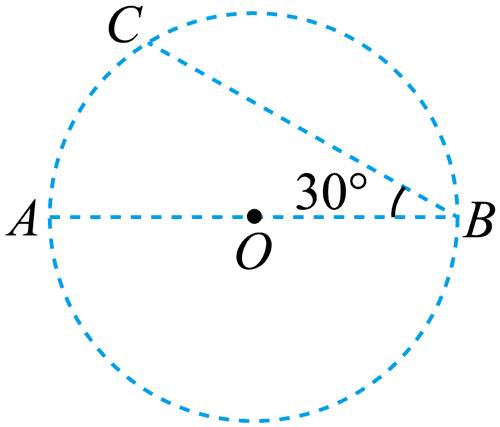．如图，A、B、C 三个点位于以 O 为圆心的圆上，直径 AB 与弦 BC 间的夹角为 30°。A、B 两点分别放有电荷量大小为 q_A、q_B 的点电荷时，C 点的电场强度方向恰好沿圆的切线方向，则 \(\frac{{{q_A}}}{{{q_B}}}\) 等于（     ）

A．\(\frac{1}{3}\)             B．\(\frac{{\sqrt 3 }}{3}\)          C．\({\sqrt 3 }\)          D．2

【答案】

B

 

8．我国在贵州平塘建成了世界最大单口径球面射电望远镜 FAST，其科学目标之一是搜索地外文明。在宇宙中，波长位于搜索地外文明的射电波段的辐射中存在两处较强的辐射，一处是波长为 21 cm 的中性氢辐射，另一处是波长为 18 cm 的羟基辐射。在真空中，这两种波长的辐射相比，中性氢辐射的光子（    ）

A．频率更大         B．能量更小         C．动量更小         D．传播速度更大

【答案】

BC

 

9．如图，一玻璃瓶的瓶塞中竖直插有一根两端开口的细长玻璃管，管中一光滑小球将瓶中气体密封，且小球处于静止状态，装置的密封性、绝热性良好。对小球施加向下的力使其偏离平衡位置，在 t = 0 时由静止释放，小球的运动可视为简谐运动，周期为 T。规定竖直向上为正方向，则小球在 t = 1.5T 时刻（    ）

A．位移最大，方向为正                     B．速度最大，方向为正

C．加速度最大，方向为负                 D．受到的回复力大小为零

【答案】

AC

【解析】

对小球施加向下的力使其偏离平衡位置，在 t = 0 时由静止释放，可知此时小球位于最低点，且小球的运动可视为简谐运动，周期为 T。则小球在 t = 1.5T 时刻处于最高点位置，此时位移最大，方向向上（正方向）；小球受到的回复力最大，方向向下，则小球的加速度最大，方向向下（负方向）；此时小球的速度为 0。

故选 AC。

 

10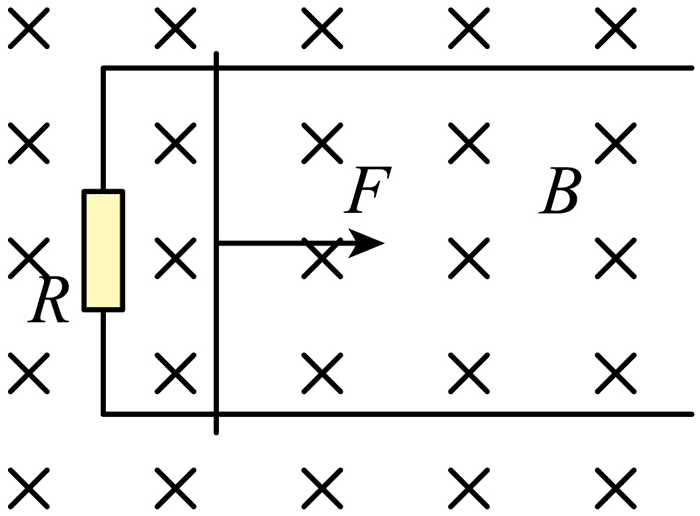．如图，间距为 L 的两根金属导轨平行放置并固定在绝缘水平桌面上，左端接有一定值电阻 R，导轨所在平面存在磁感应强度大小为 B、方向竖直向下的匀强磁场。质量为 m 的金属棒置于导轨上，在水平拉力作用下从静止开始做匀加速直线运动，一段时间后撤去水平拉力，金属棒最终停在导轨上。已知金属棒在运动过程中，最大速度为 v，加速阶段的位移与减速阶段的位移相等，金属棒始终与导轨垂直且接触良好，不计摩擦及金属棒与导轨的电阻，则（    ）

A．加速过程中通过金属棒的电荷量为 \(\frac{{mv}}{{qB}}\)             B．金属棒加速的时间为 \(\frac{{2mR}}{{{B^2}{L^2}}}\)

C．加速过程中拉力的最大值为 \(\frac{{4{B^2}{L^2}v}}{{3R}}\)                   D．加速过程中拉力做的功为 \(\frac{1}{2}\)mv²

【答案】

AB

 

11．智能手机内置很多传感器，磁传感器是其中一种。现用智能手机内的磁传感器结合某应用软件，利用长直木条的自由落体运动测量重力加速度。主要步骤如下：

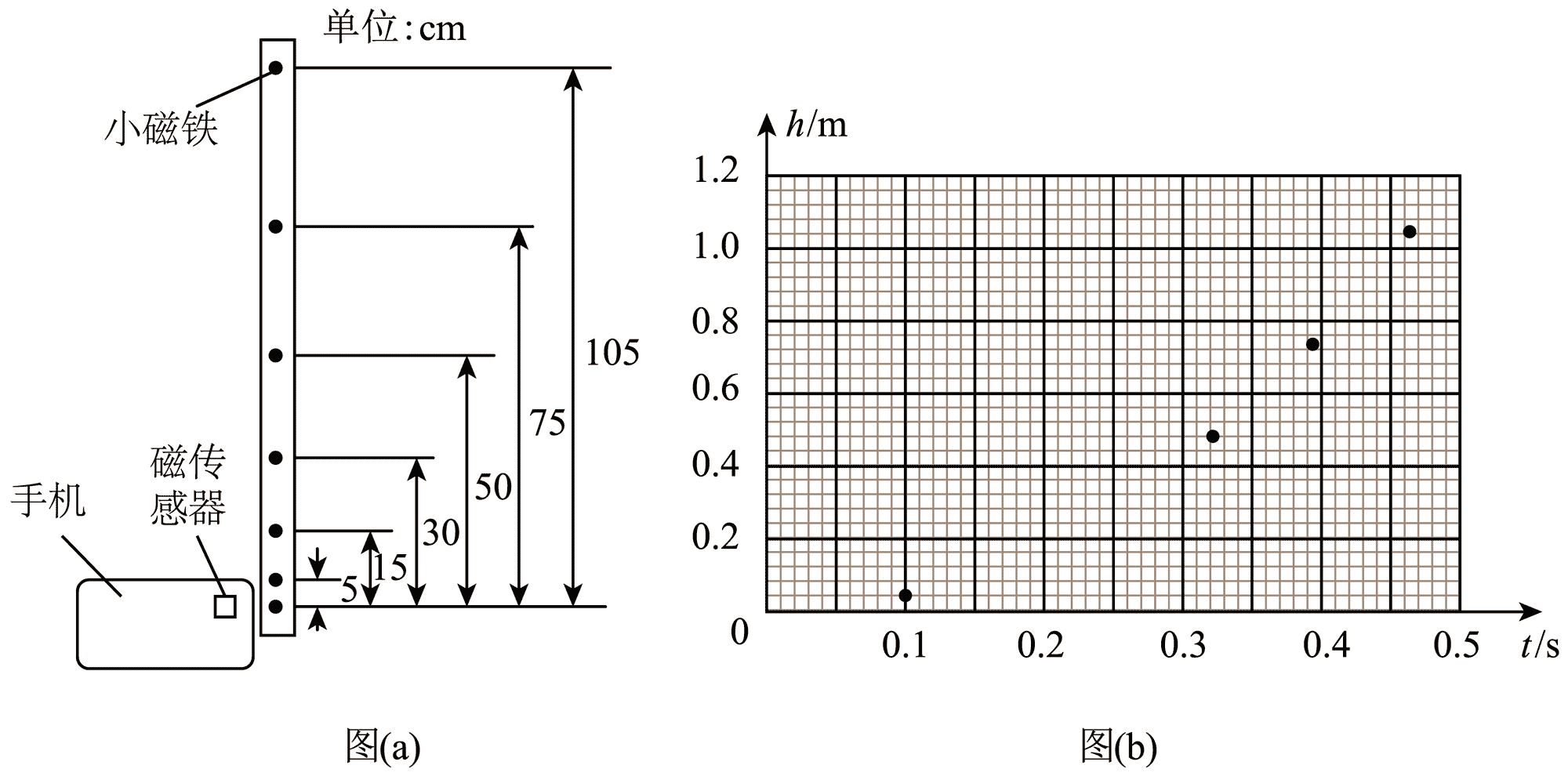
（1）在长直木条内嵌入 7 片小磁铁，最下端小磁铁与其他小磁铁间的距离如图（a）所示。

（2）开启磁传感器，让木条最下端的小磁铁靠近该磁传感器，然后让木条从静止开始沿竖直方向自由下落。

（3）以木条释放瞬间为计时起点，记录下各小磁铁经过传感器的时刻，数据如下表所示：

h(m)	0.00	0.05	0.15	0.30	0.50	0.75	1.05
t(s)	0.000	0.101	0.175	0.247	0.319	0.391	0.462

（4）根据表中数据，在答题卡上补全图（b）中的数据点，并用平滑曲线绘制下落高度h随时间 t 变化的 h–t 图线_____。

（5）由绘制的 h–t 图线可知，下落高度随时间的变化是_____（填“线性”或“非线性”）关系。

（6）将表中数据利用计算机拟合出下落高度 h 与时间的平方 t² 的函数关系式为 h = 4.916t²(SI)。据此函数可得重力加速度大小为_____m/s²。（结果保留 3 位有效数字）

【答案】

（4）

（5）非线性

（6）9.83

 

12．某实验小组根据热敏电阻的阻值随温度变化的规律，探测温度控制室内的温度。选用的器材有：

热敏电阻 R₁；

电流表 G（内阻 R_g 为 240 Ω，满偏电流为 I_g）；

定值电阻 R（阻值为 48 Ω）；

电阻箱 R₀（阻值 0 ~ 999.9 Ω）；

电源 E（电动势恒定，内阻不计）；

单刀双掷开关 S₁、单刀单掷开关 S₂；导线若干。

请完成下列步骤：

（1）该小组设计了如图（a）所示的电路图。根据图（a），在答题卡上完成图（b）中的实物图连线。

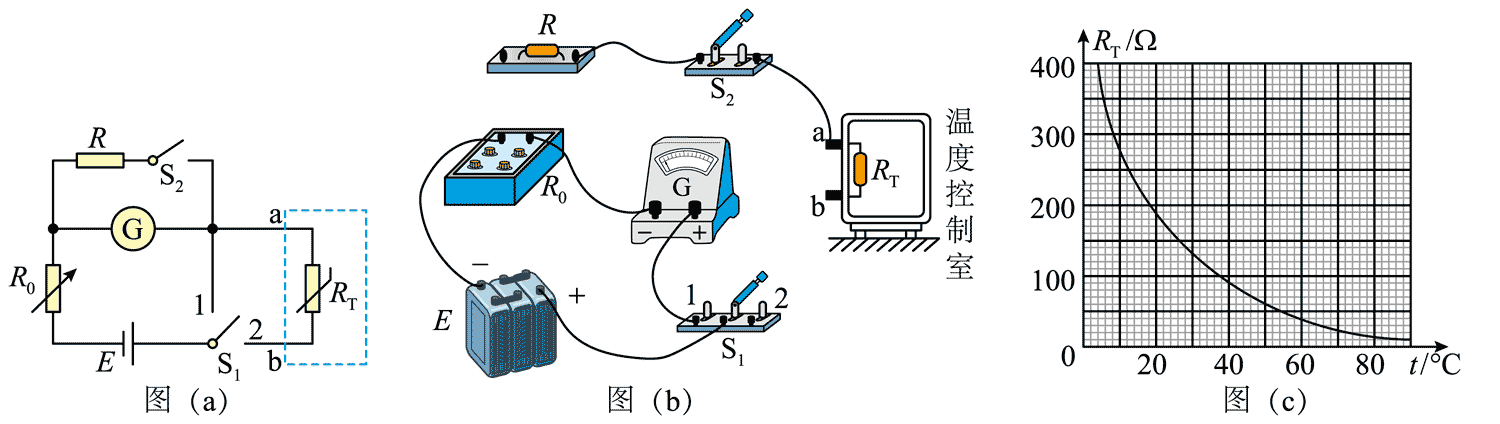
（2）开关 S₁、S₂ 开，将电阻箱的阻值调到_____（填“最大”或“最小”）。开关 S₁ 接 1，调节电阻箱，当电阻箱读数为 60.0 Ω 时，电流表示数为 I_g。再将 S₁ 改接 2，电流表示数为 \(\frac{{{I_g}}}{2}\)，断开 S₁。得到此时热敏电阻 R₁ 的阻值为_____Ω。

（3）该热敏电阻 R₁ 阻值随温度 t 变化的 R₁ – t 曲线如图（c）所示，结合（2）中的结果得到温度控制室内此时的温度约为_____℃。（结果取整数）

（4）开关 S₁ 接 1，闭合 S₂，调节电阻箱，使电流表示数为 I_g。再将 S₁ 改接 2，如果电流表示数为 \(\frac{{{I_g}}}{k}\)（k > 1），则此时热敏电阻 R₁ = _____Ω（用 k 表示），根据图（c）即可得到此时温度控制室内的温度。

【答案】

（1）

（2）最大，300

（3）9

（4）50(k − 1)

 

13．制作水火箭是青少年科技活动的常见项目之一。某研究小组为了探究水火箭在充气与喷水过程中气体的热学规律，把水火箭的塑料容器竖直固定，其中 A、C 分别是塑料容器的充气口、喷水口，B 是气压计，如图（a）所示。在室温环境下，容器内装入一定质量的水，此时容器内的气体体积为 V₀，压强为 p₀，现缓慢充气后压强变为 4p₀，不计容器的容积变化。

（1）设充气过程中气体温度不变，求充入的气体在该室温环境下压强为 p₀ 时的体积。

（2）打开喷水口阀门，喷出一部分水后关闭阀门，容器内气体从状态 M 变化到状态 N，其压强 p 与体积 V 的变化关系如图（b）中实线所示，已知气体在状态 N 时的体积为 V₁，压强为 p₁。求气体在状态 N 与状态 M 时的热力学温度之比。

（3）图（b）中虚线 MNʹ 是容器内气体在绝热（既不吸热也不放热）条件下压强 p 与体积 V 的变化关系图线，试判断气体在图（b）中沿实线从 M 到 N 的过程是吸热还是放热。（不需要说明理由）

【答案】

（1）3V₀

（2）\(\frac{{{p_1}{V_1}}}{{4{p_0}{V_0}}}\)

（3）吸热

 

14．如图，边长为 L 的正方形 abcd 区域及矩形 cdef 区域内均存在电场强度大小为 E、方向竖直向下且与 ab 边平行的匀强电场，ef 右边有一半径为 \(\frac{{\sqrt 3 }}{3}\)L 且与 ef 相切的圆形区域，切点为 ef 的中点，该圆形区域与 cdef 区域内均存在磁感应强度大小为 B、方向垂直纸面向里的匀强磁场。一带电粒子从 b 点斜向上射入电场后沿图中曲线运动，经 cd 边的中点进入 cdef 区域，并沿直线通过该区域后进入圆形区域。所有区域均在纸面内，粒子始终在该纸面内运动，不计粒子重力。求：

（1）粒子沿直线通过 cdef 区域时的速度大小；

（2）粒子的电荷量与质量之比；

（3）粒子射出圆形区域时速度方向与进入圆形区域时速度方向的夹角。

【答案】

（1）\(\frac{E}{B}\)

（2）\(\frac{E}{{L{B^2}}}\)

（3）60°

 

15．如图，半径为 R = 1.8 m 的四分之一光滑圆轨道固定在竖直平面内，其末端与水平地面 PM 相切于 P 点，PM 的长度 d = 2.7 m。一长为 L = 3.3 m 的水平传送带以恒定速率 v₀ = 1 m/s 逆时针转动，其右端与地面在 M 点无缝对接。物块 a 从圆轨道顶端由静止释放，沿轨道下滑至 P 点，再向左做直线运动至 M 点与静止的物块 b 发生弹性正碰，碰撞时间极短。碰撞后 b 向左运动到达传送带的左端 N 时，瞬间给 b 一水平向右的冲量 I，其大小为 6 N·s。以后每隔 Δt = 0.6 s 给 b 一相同的瞬时冲量 I，直到 b 离开传送带。已知 a 的质量为 m_a = 1 kg，b 的质量为 m_b = 2 kg，它们均可视为质点。a、b 与地面及传送带间的动摩擦因数均为 μ = 0.5，取重力加速度大小 g = 10 m/s²。求：

（1）a 运动到圆轨道底端时轨道对它的支持力大小；

（2）b 从 M 运动到 N 的时间；

（3）b 从 N 运动到 M 的过程中与传送带摩擦产生的热量。

【答案】

（1）30 N

（2）3.2 s

（3）95 J