1．下列物理量中，属于矢量的是（     ）

A．位移                  B．时间                  C．电流                 D．热量

【答案】

A

【解析】

A．位移既有大小又有方向，且运算法则为平行四边形法则，是矢量，故A正确；

BD．时间和热量均只有大小没有方向，是标量，故 BD 错误；

C．电流运算法则是算术法则，是标量，故 C 错误。

故选 A。

 

2．如图为小猫蹬地跃起腾空追蝶的情景，则（    ）

A．飞行的蝴蝶只受重力的作用

B．蝴蝶转弯时所受合力沿运动方向

C．小猫在空中受重力和弹力的作用

D．小猫蹬地时弹力大于所受重力

【答案】

D

【解析】

A．飞行的蝴蝶除了受到重力的作用还受到空气的作用力，故 A 错误；

B．蝴蝶转弯时做曲线运动，所受合力与速度方向不在一条直线上，故 B 错误；

C．小猫在空中与其他物体间没有接触，不受弹力的作用，故 C 错误；

D．小猫蹬地时有向上的加速过程，故弹力大于所受重力，故 D 正确。

故选 D。

 

3．如图为水流导光实验，出水口受激光照射，下面桶中的水被照亮，则（    ）

A．激光在水和空气中速度相同

B．激光在水流中有全反射现象

C．水在空中做匀速率曲线运动

D．水在水平方向做匀加速运动

【答案】

B

【解析】

A．光在介质中的速度为 v = c/n，故激光在水中的传播速度小于在空气中的传播速度，故 A 错误；

B．水流导光的原理为光在水中射到水与空气分界面时入射角大于临界角，发生了全反射，故 B 正确；

C．水在空中只受到重力作用，做匀变速曲线运动，速度在增大，故 C 错误；

D．水在水平方向做匀速直线运动，故 D 错误。

故选 B。

 

4．发现中子的核反应方程为 ⁴₂He + ⁹₄Be→X + ¹₀n，“玉兔二号”巡视器的核电池中钚 238的衰变方程为 ²³⁸₉₄Pu→²³⁴₉₂U + Y，下列正确的是（    ）

A．核反应方程中的 X 为 ¹²₆C                  B．衰变方程中的 Y 为 ³₂He

C．中子 ¹₀n 的质量数为零                  D．钚 238 的衰变吸收能量

【答案】

A

【解析】

AB．根据质量数和电荷数守恒可知 X 为 ¹²₆C，Y 为 ⁴₂He，故 A 正确，B 错误；

C．中子的质量数为 1，故 C 错误；

D．衰变过程中质量亏损，释放能量，故 D 错误。

故选 A。

 

5．一个音乐喷泉喷头出水口的横截面积为 2×10⁻⁴ m²，喷水速度约为 10 m/s，水的密度为 1×10³ kg/m³，则该喷头喷水的功率约为（     ）

A．10 W                 B．20 W                 C．100 W                       D．200 W

【答案】

C

 

6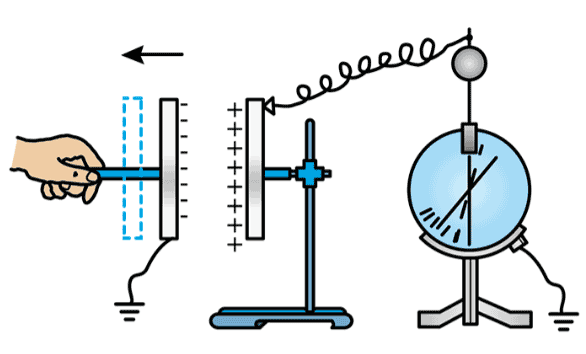．图示是“研究电容器两极板间距对电容大小的影响”实验，保持电荷量不变，当极板间距增大时，静电计指针张角增大，则（    ）

A．极板间电势差减小                  B．电容器的电容增大

C．极板间电场强度增大              D．电容器储存能量增大

【答案】

D

 

7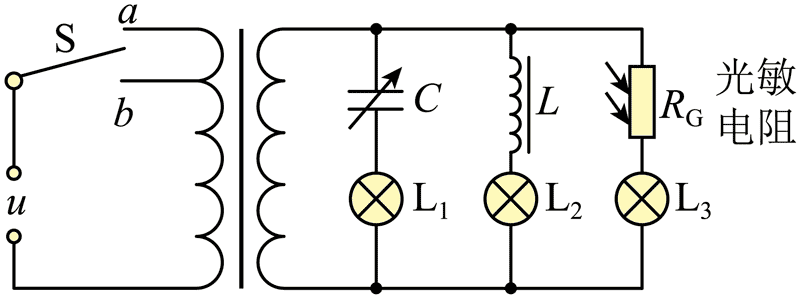．理想变压器的原线圈通过 a 或 b 与频率为 f、电压为 u 的交流电源连接，副线圈接有三个支路、如图所示。当 S 接 a 时，三个灯泡均发光，若（     ）

A．电容 C 增大，L₁ 灯泡变亮                  B．频率 f 增大，L₂ 灯泡变亮

C．R_G 上光照增强，L₃ 灯泡变暗              D．S 接到 b 时，三个泡均变暗

【答案】

A

【解析】

A．电容增大，对交流电的阻碍作用减小，则 L₁ 灯泡变亮，故 A 正确；

B．频率 f 增大，则电感的阻碍作用增大，则 L₂ 灯泡变暗，故 B 错误；

C．光敏电阻光照增强，阻值减小，由于各支路电压不变，则 L₃ 灯泡电流增大，变亮，故C错误；

D．S 接到 b 时，根据变压比可知，副线圈电压增大，则三个泡均变亮，故 D 错误。

故选 A。

 

8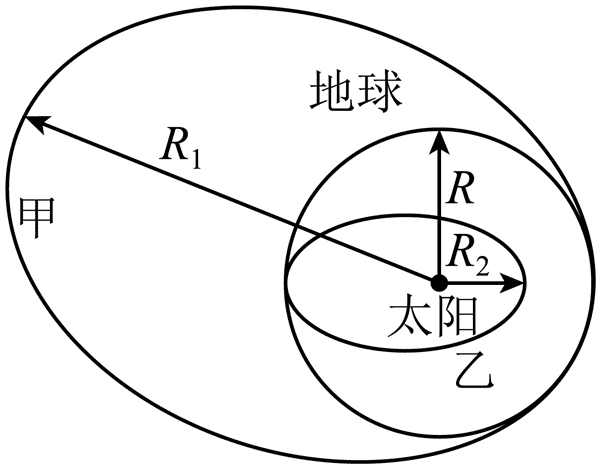．与地球公转轨道“外切”的小行星甲和“内切”的小行星乙的公转轨道如图所示，假设这些小行星与地球的公转轨道都在同一平面内，地球的公转半径为 R，小行星甲的远日点到太阳的距离为 R₁，小行星乙的近日点到太阳的距离为 R₂，则（     ）

A．小行星甲在远日点的速度大于近日点的速度

B．小行星乙在远日点的加速度小于地球公转加速度

C．小行星甲与乙的运行周期之比 \(\frac{{{T_1}}}{{{T_2}}}\) = \(\sqrt {\frac{{R_1^3}}{{R_2^3}}} \)

D．甲乙两星从远日点到近日点的时间之比 \(\frac{{{t_1}}}{{{t_2}}}\) = \(\sqrt {\frac{{{{({R_1} + R)}^3}}}{{{{({R_2} + R)}^3}}}} \)

【答案】

D

 

9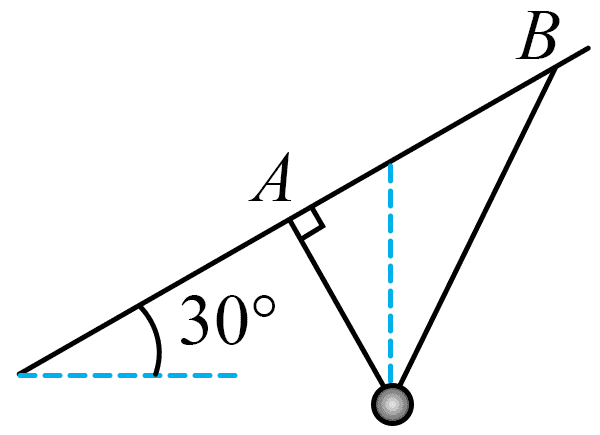．如图所示，不可伸长的光滑细线穿过质量为 0.1 kg 的小铁球，两端 A、B 悬挂在倾角 为 30° 的固定斜杆上，间距为 1.5 m。小球平衡时，A 端细线与杆垂直；当小球受到垂直纸面方向的扰动做微小摆动时，等效于悬挂点位于小球重垂线与 AB 交点的单摆，重力加速度 g = 10 m/s²，则（     ）

A．摆角变小，周期变大                               B．小球摆动周期约为 2 s

C．小球平衡时，A 端拉力为 \(\frac{{\sqrt 3 }}{2}\) N         D．小球平衡时，A 端拉力小于 B 端拉力

【答案】

B

 

10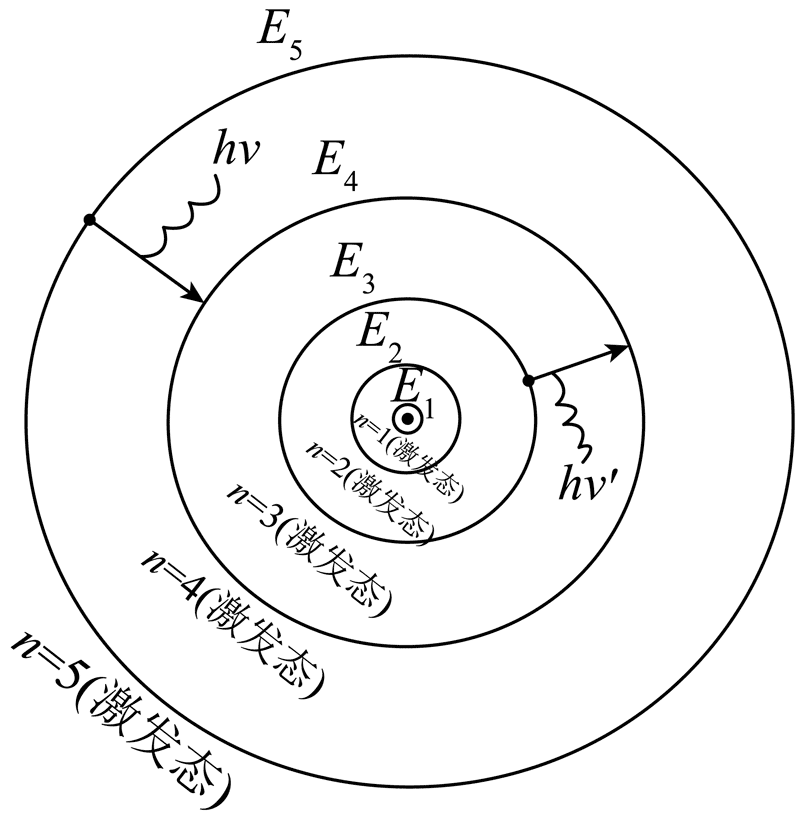．玻尔氢原子电子轨道示意图如图所示，处于 n = 3 能级的原子向低能级跃迁，会产生三种频率为 ν₃₁、ν₃₂、ν₂₁ 的光，下标数字表示相应的能级。已知普朗克常量为 h，光速为 c。正确的是（     ）

A．频率为 ν₃₁ 的光，其动量为 \(\frac{{{E_3} - {E_1}}}{{hc}}\)

B．频率为 ν₃₁ 和 ν₂₁ 的两种光分别射入同一光电效应装置，均产生光电子，其最大初动能之差为 hν₃₂

C．频率为 ν₃₁ 和 ν₂₁ 的两种光分别射入双缝间距为 d，双缝到屏的距离为 L 的干涉装置，产生的干涉条纹间距之差为 \(\frac{{Lc}}{{d{\nu _{32}}}}\)

D．若原子 n = 3 跃迁至 n = 4 能级，入射光的频率 ν₃₄ʹ > \(\frac{{{E_4} - {E_3}}}{h}\)

【答案】

B

 

11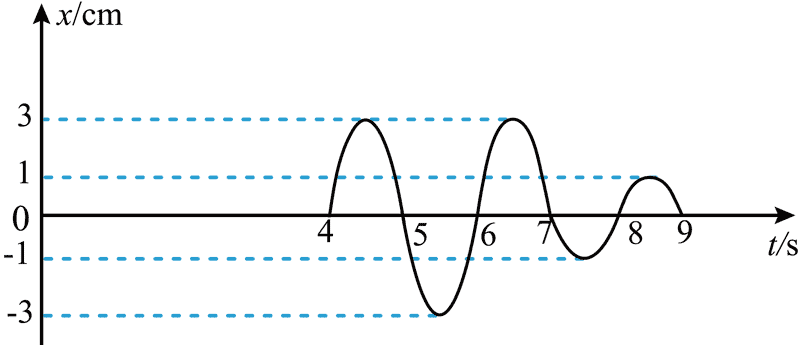．频率相同的简谐波源 S₁、S₂ 和接收点 M 位于同一平面内，S₁、S₂ 到 M 的距离之差为 6 m。t = 0 时 S₁、S₂ 同时垂直平面开始振动，M 点的振动图像如图所示，则（    ）

A．两列波的波长为 2 m                                       B．两列波的起振方向均沿 x 正方向

C．S₁ 和 S₂ 在平面内不能产生干涉现象         D．两列波的振幅分别为 3 cm 和 1 cm

【答案】

B

 

12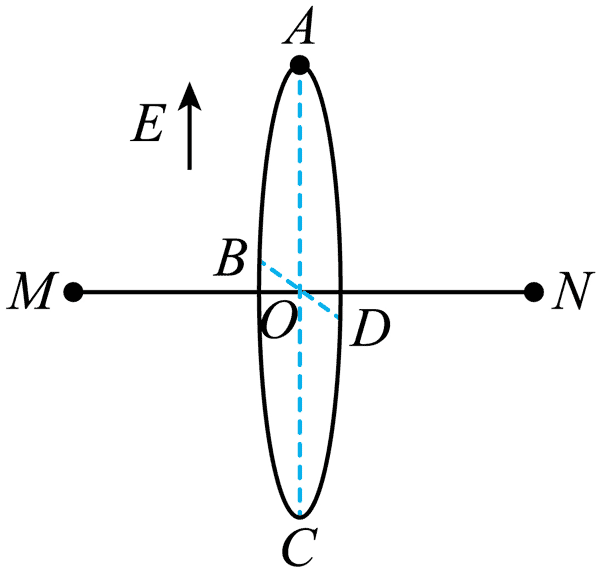．如图所示空间原有大小为 E、方向竖直向上的匀强电场，在此空间同一水平面的 M、N 点固定两个等量异种点电荷，绝缘光滑圆环 ABCD 垂直 MN 放置，其圆心 O 在 MN 的中点，半径为 R、AC 和 BD 分别为竖直和水平的直径。质量为 m、电荷量为 + q 的小球套在圆环上，从 A 点沿圆环以初速度 v₀ 做完整的圆周运动，则（     ）

A．小球从 A 到 C 的过程中电势能减少

B．小球不可能沿圆环做匀速圆周运动

C．可求出小球运动到 B 点时的加速度

D．小球在 D 点受到圆环的作用力方向平行 MN

【答案】

 C

 

13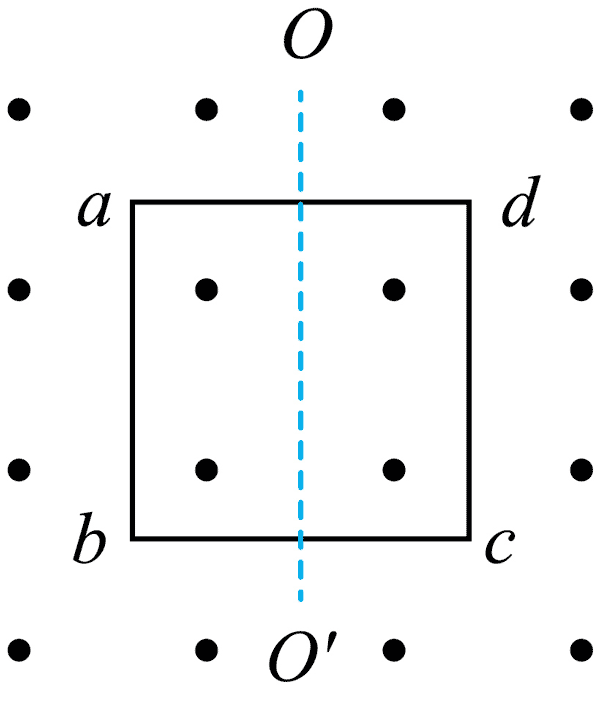．如图所示，边长为 1 m、电阻为 0.04 Ω 的刚性正方形线框 abcd 放在匀强磁场中，线框平面与磁场 B 垂直。若线框固定不动，磁感应强度以 \(\frac{{\Delta B}}{{\Delta t}}\) = 0.1 T/s 均匀增大时，线框的发热功率为 P；若磁感应强度恒为 0.2 T，线框以某一角速度绕其中心轴 OOʹ 匀速转动时，线框的发热功率为 2P，则 ab 边所受最大的安培力为（     ）

A．\(\frac{1}{2}\) N                   B．\(\frac{{\sqrt 2 }}{2}\) N                         C．1 N                    D．\(\sqrt 2 \) N

【答案】

C

 

14．下列说法正确的是（    ）

A．中子整体呈电中性但内部有复杂结构

B．真空中的光速在不同的惯性参考系中大小都相同

C．增加接收电路的线圈匝数，可接收更高频率的电台信号

D．分子间作用力从斥力变为引力的过程中，分子势能先增加后减少

【答案】

AB

 

15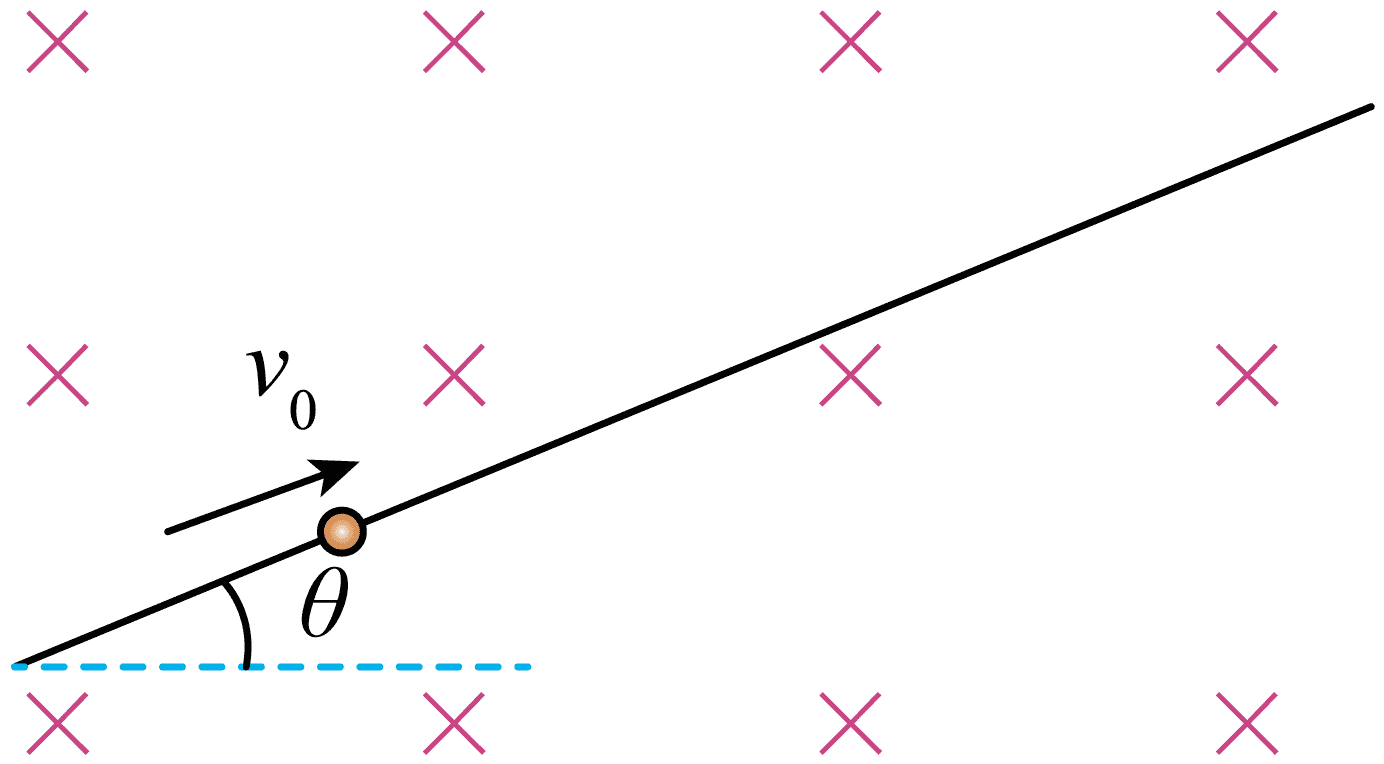．如图所示，一根固定的足够长的光滑绝缘细杆与水平面成 θ 角。质量为 m、电荷量为 + q 的带电小球套在细杆上。小球始终处于磁感应强度大小为 B 的匀强磁场中。磁场方向垂直细杆所在的竖直面，不计空气阻力。小球以初速度 v₀ 沿细杆向上运动至最高点，则该过程（     ）

A．合力冲量大小为 mv₀cosθ                       B．重力冲量大小为 mv₀sinθ

C．洛伦兹力冲量大小为 \(\frac{{qBv_0^2}}{{2g\sin \theta }}\)                D．若 v₀ = \(\frac{{2mg\cos \theta }}{{qB}}\)，弹力冲量为零

【答案】

CD

 

16．在“验证机械能守恒定律”的实验中，

（1）下列操作正确的是_______。

（2）实验获得一条纸带，截取点迹清晰的一段并测得数据如图所示。

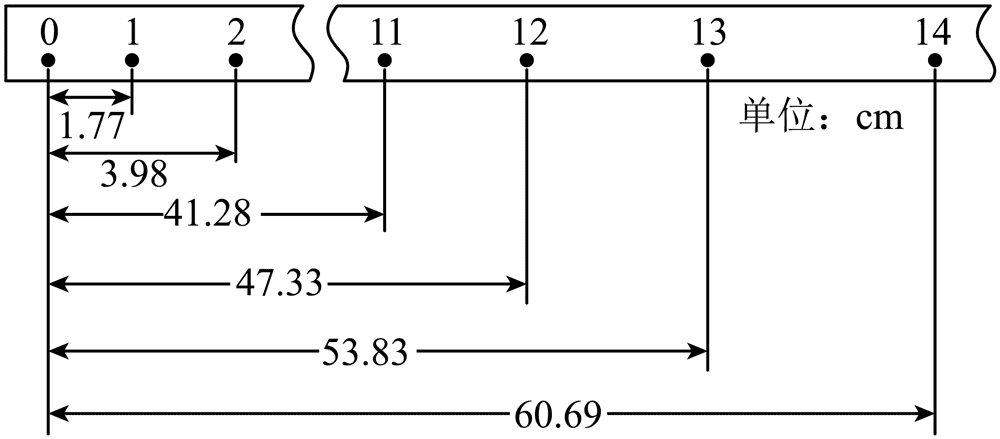
已知打点的频率为 50 Hz，则打点“13”时，重锤下落的速度大小为_____m/s（保留三位有效数字）。

（3）某同学用纸带的数据求出重力加速度 g = 9.77 m/s²，并用此 g 值计算得出打点“1”到“13”过程重锤的重力势能减小值为 5.09m，另计算得动能增加值为 5.08m（m 为重锤质量），则该结果______（选填“能”或“不能”验证机械能守恒，理由是（    ）

A．在误差允许范围内

B．没有用当地的重力加速度 g

【答案】

（1）B

（2）3.34

（3）能，A

 

16．在测绘发光二极管在导通状态下的伏安特性曲线实验中，

（1）用多用电表欧姆挡判断发光二极管的正负极选用 ×100 挡时，变换表笔与二极管两极的连接方式，发现电表指针均不偏转。选用挡_______（选填”×10”或“×1 k”）重新测试，指针仍不偏转，更换二极管极性后，发现指针偏转，此时与多用电表红色表笔相连的是二极管_________（选填“正极”或“负极”）。

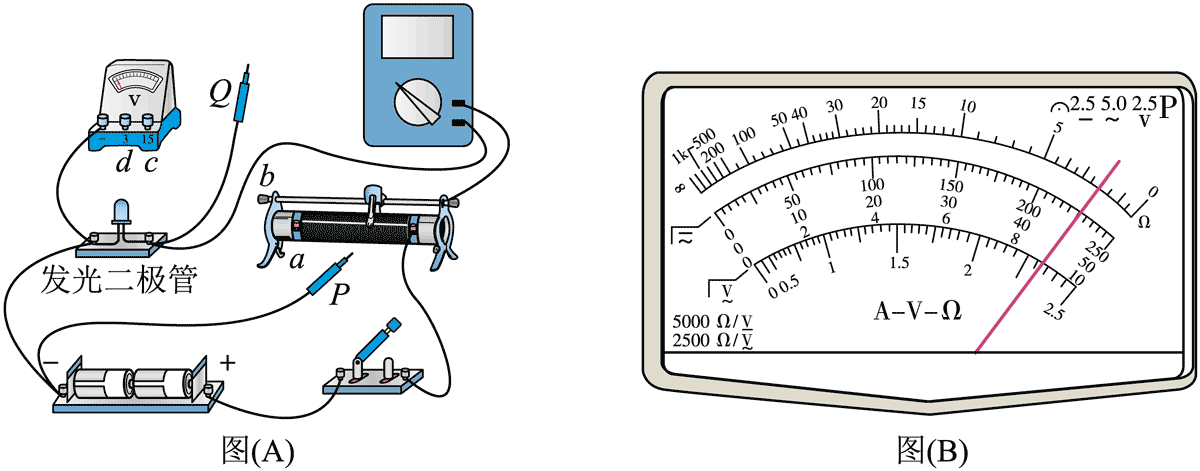
（2）图（A）是已完成部分连线的实物图，为实现电压可从零开始调节，并完成实验，P 应连接________接线柱（选填“a”“b”“c”或“d”），Q 应连接_________接线柱（选填“a”、“b”、“c”或“d”）。某次选用多用电表量程为 50 mA 挡测量，指针如图（B）所示，则电流 I = _______mA

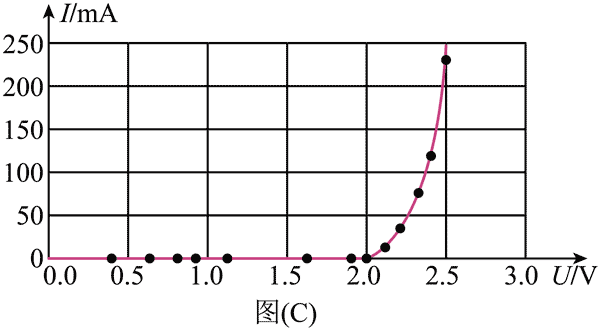
（3）根据测得数据，绘出伏安特性曲线如图（C）所示，说明该二极管是__________元件（选填“线性”或“非线性”），正常发光时电压在_________V 范围。

【答案】

（1）×1 k，负极

（2）a，d，45.0

（3）非线性，1.9 ~ 2.5

【解析】

（1）指针未偏转，说明可能电阻过大，应换用“×1 k”挡继续实验；根据“红进黑出”原则及二极管单向导电性可知红色表笔相连的是二极管负极。

（2）实现电压可从零开始调节，滑动变阻器采用分压式接法，P 应连接 a；根据图 C 可知电压表选取 0 ~ 3 V 量程，故 Q 接 d；

多用电表量程为 50 mA，分度值为 1 mA，需要估读到 0.1 mA，故电表的读数为 45.0 mA

（3）根据图像可知 I 随 U 非线性变化，故说明该二极管是非线性元件，根据图像可知正常发光时即有电流通过时电压在 1.9 V ~ 2.5 V 范围。

 

16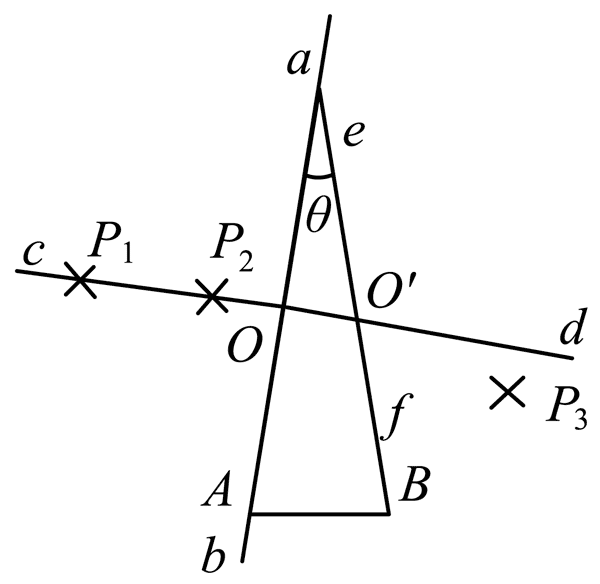．如图所示，用“插针法”测量一等腰三角形玻璃砖（侧面分别记为 A 和 B、顶角大小为 θ）的折射率。

①在白纸上画一条直线 ab，并画出其垂线 cd，交于 O 点；

②将侧面 A 沿 ab 放置，并确定侧面 B 的位置 ef；

③在 cd 上竖直插上大头针 P₁ 和 P₂，从侧面 B 透过玻璃砖观察 P₁ 和 P₂，插上大头针 P₃，要求 P₃ 能挡住__________（选填“P₁”、“P₂”或“P₁ 和 P₂”）的虚像；

④确定出射光线的位置____________（选填“需要”或“不需要”第四枚大头针；

⑤撤去玻璃砖和大头针，测得出射光线与直线 ef 的夹角为 α，则玻璃砖折射率 n = ____________________。

【答案】

③P₁ 和 P₂

④不需要

⑤\(\frac{{\cos \alpha }}{{\sin \theta }}\)

【解析】

③要求 P₁ 和 P₂ 在一条光线上，该光线透过玻璃砖后过 P₃，故 P₃ 要能挡住 P₁ 和 P₂ 的虚像；

④cd 与 ab 垂直，则过 P₁ 和 P₂ 的光线与 ab 垂直，光垂直入射时传播方向不变，可确定 ef 边上的入射点，此时只需要找到折射光线上的一点即可确定出射光线，不需要插第四枚大头针；

⑤根据几何关系可知入射角为 θ，折射角为 \(\frac{\pi }{2}\) − α，故

n = \(\frac{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}}{{\sin \theta }}\) = \(\frac{{\cos \alpha }}{{\sin \theta }}\)

 

17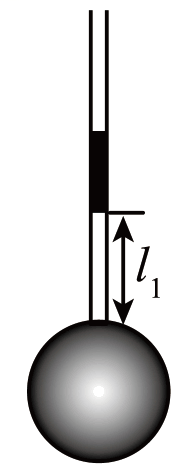．如图所示，测定一个形状不规则小块固体体积，将此小块固体放入已知容积为 V₀ 的导热效果良好的容器中，开口处竖直插入两端开口的薄玻璃管，其横截面积为 S，接口用蜡密封。容器内充入一定质量的理想气体，并用质量为 m 的活塞封闭，活塞能无摩擦滑动，稳定后测出气柱长度为 l₁，将此容器放入热水中，活塞缓慢竖直向上移动，再次稳定后气柱长度为 l₂、温度为 T₂。已知 S = 4.0×10⁻⁴ m²，m = 0.1 kg，l₁ = 0.2 m，l₂ = 0.3 m，T₂ = 350 K，V₀ = 2.0×10⁻⁴ m³，大气压强 p₀ = 1.0×10⁵ Pa，环境温度 T₁ = 300 K。

（1）在此过程中器壁单位面积所受气体分子的平均作用力________（选填“变大”“变小”或“不变”），气体分子的数密度_______（选填“变大”“变小”或“不变”）；

（2）求此不规则小块固体的体积 V；

（3）若此过程中气体内能增加 10.3 J，求吸收热量 Q。

【答案】

（1）不变，变小

（2）4×10⁻⁵ m³

（3）14.4 J

 

18．一弹射游戏装置竖直截面如图所示，固定的光滑水平直轨道 AB、半径为 R 的光滑螺旋圆形轨道 BCD、光滑水平直轨道 DE 平滑连接。长为 L、质量为 M 的平板紧靠长为 d 的固定凹槽 EFGH 侧壁 EF 放置，平板上表面与 DEH 齐平。将一质量为 m 的小滑块从 A 端弹射，经过轨道 BCD 后滑上平板并带动平板一起运动，平板到达 HG 即被锁定。已知 R = 0.5 m，d = 4.4 m，L = 1.8 m，M = m = 0.1 kg，平板与滑块间的动摩擦因数 μ₁ = 0.6、与凹槽水平底面 FG 间的动摩擦因数为 μ₂。滑块视为质点，不计空气阻力，最大静摩擦力等于滑动摩擦力，重力加速度 g = 10 m/s²。

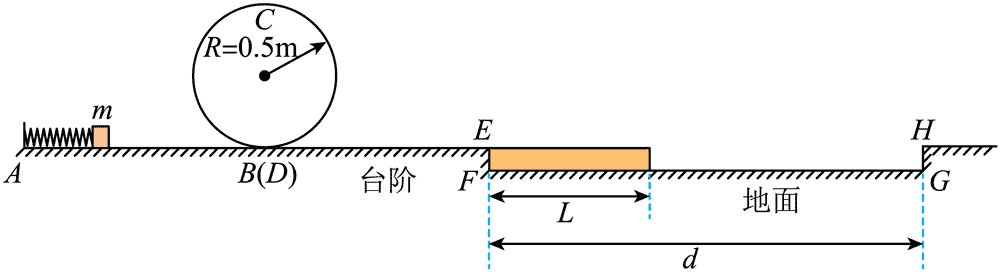
（1）滑块恰好能通过圆形轨道最高点 C 时，求滑块离开弹簧时速度 v₀ 的大小；

（2）若 μ₂ = 0，滑块恰好过 C 点后，求平板加速至与滑块共速时系统损耗的机械能；

（3）若 μ₂ = 0.1，滑块能到达 H 点，求其离开弹簧时的最大速度 v_m。

【答案】

（1）5 m/s

（2）0.625 J

（3）6 m/s

 

19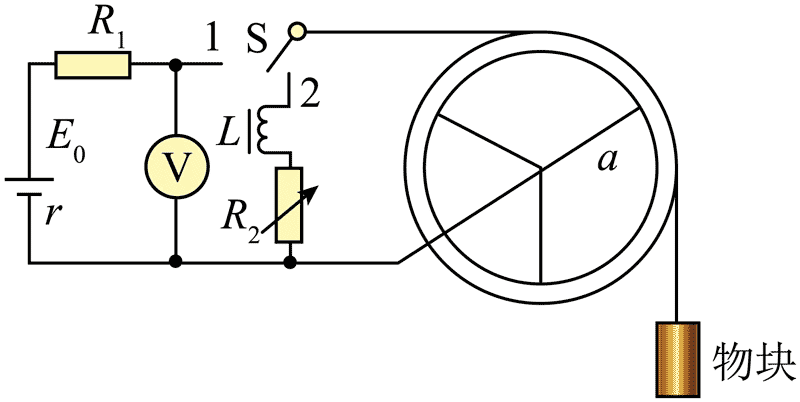．某小组探究“法拉第圆盘发电机与电动机的功用”，设计了如图所示装置。飞轮由三根长 a = 0.8 m 的辐条和金属圆环组成，可绕过其中心的水平固定轴转动，不可伸长细绳绕在圆环上，系着质量 m = 1 kg 的物块，细绳与圆环无相对滑动。飞轮处在方向垂直环面的匀强磁场中，左侧电路通过电刷与转轴和圆环边缘良好接触，开关 S 可分别与图示中的电路连接。已知电源电动势 E₀ = 12 V、内阻 r = 0.1 Ω、限流电阻 R₁ = 0.3 Ω、飞轮每根辐条电阻 R = 0.9 Ω，电路中还有可调电阻 R₂（待求）和电感 L，不计其他电阻和阻力损耗，不计飞轮转轴大小。

（1）开关 S 掷 1，“电动机”提升物块匀速上升时，理想电压表示数 U = 8 V。

①判断磁场方向，并求流过电阻 R₁ 的电流 I；

②求物块匀速上升的速度 v。

（2）开关 S 掷 2，物块从静止开始下落，经过一段时间后，物块匀速下降的速度与“电动机”匀速提升物块的速度大小相等，

①求可调电阻 R₂ 的阻值；

②求磁感应强度 B 的大小。

【答案】

（1）①垂直纸面向外，10 A               ②5 m/s

（2）①0.2 Ω         ②2.5 T

 

20．探究性学习小组设计了一个能在喷镀板的上下表面喷镀不同离子的实验装置，截面如图所示。在 xOy 平面内，除 x 轴和虚线之间的区域外，存在磁感应强度大小为 B，方向垂直纸面向外的匀强磁场，在无磁场区域内，沿着 x 轴依次放置离子源、长度为 L 的喷镀板 P、长度均为 L 的栅极板 M 和 N（由金属细丝组成的网状电极），喷镀板 P 上表面中点 Q 的坐标为（1.5L，0），栅极板 M 中点 S 的坐标为（3L，0），离子源产生 a 和 b 两种正离子，其中 a 离子质量为 m，电荷量为 q，b 离子的比荷为 a 离子的 \(\frac{1}{4}\) 倍，经电压 U = kU₀（其中 U₀ = \(\frac{{{B^2}q{L^2}}}{{8m}}\)，k 大小可调，a 和 b 离子初速度视为 0）的电场加速后，沿着 y 轴射入上方磁场。经磁场偏转和栅极板 N 和 M 间电压 U_NM 调控（U_NM > 0），a 和 b 离子分别落在喷镀板的上下表面，并立即被吸收且电中和，忽略场的边界效应、离子受到的重力及离子间相互作用力。

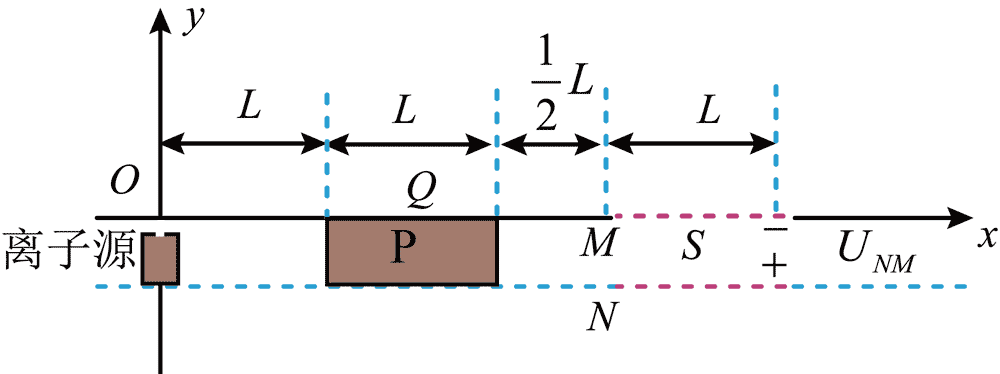
（1）若 U = \(\frac{3}{4}\)U₀，求 a 离子经磁场偏转后，到达 x 轴上的位置 x₀（用 L 表示）。

（2）调节 U 和 U_NM，并保持 U_MN = U，使 a 离子能落到喷镀板 P 上表面任意位置，求：

①U 的调节范围（用 U₀ 表示）；

②b 离子落在喷镀板 P 下表面的区域长度；

（3）要求 a 和 b 离子恰好分别落在喷镀板 P 上下表面的中点，求 U 和 U_NM 的大小。

【答案】

（1）L

（2）①U₀ ≤ U ≤ 4U₀；②\(\frac{1}{2}\)L

（3）U = \(\frac{{{9B^2}q{L^2}}}{{32m}}\)，U_MN = \(\frac{{{27B^2}q{L^2}}}{{128m}}\) 或 \(\frac{{{27B^2}q{L^2}}}{{256m}}\) 或 \(\frac{{{9B^2}q{L^2}}}{{128m}}\)