1．电荷

我们把最小电荷量叫做元电荷，用符号 e 表示，通常 e 取 1.6×10⁻¹⁹ C。静电力常量为 k。

 

1．电容器能存储和释放电荷。用图（a）电路对电容器进行充放电实验，充电时应将单刀双掷开关 S 置于接线柱________。改变电路中电阻 R 的阻值对该电容器进行两次充电，对应电容器的电荷量 q 随时间 t 变化的 q – t 曲线分别如图（b）中①、②所示。对应快速充电过程的是图线________，对应电阻 R 阻值较小的是图线________。

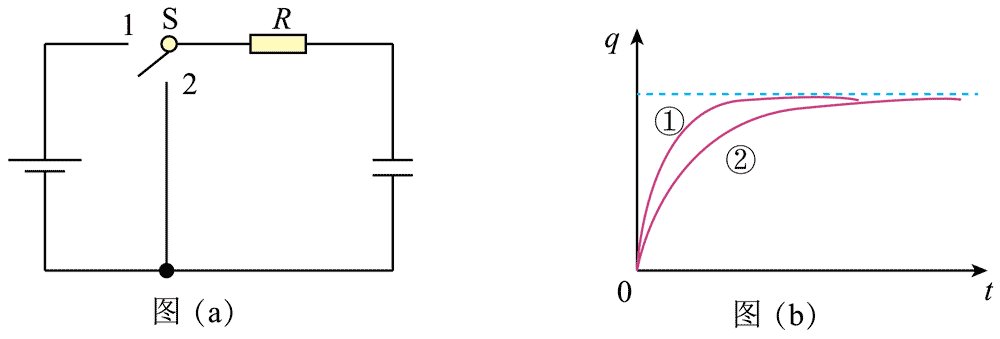
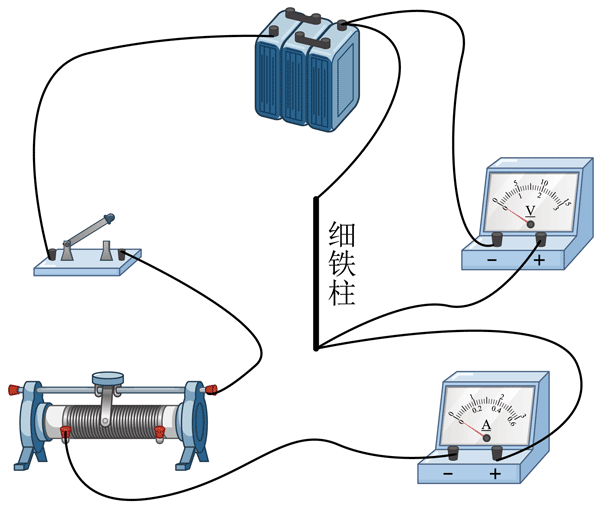
2．电荷定向移动产生电流，电阻反映了导体对电流的阻碍作用。请在所给的实验器材图上补上合适的连线，完成“用伏安法测量待测细铁丝的电阻”的电路图。

 

3．氢原子由带正电的原子核和核外带负电的电子组成。电子在原子核对其库仑力作用下绕核做匀速圆周运动，与卫星在行星的万有引力作用下绕行星的圆周运动规律类似。若电子绕氢原子核做匀速圆周运动的半径为 a，则

（1）电子的运动周期（    ）

A．T ∝ a^2/3         B．T ∝ a²            C．T ∝ a^1/2          D．T ∝ a^3/2

（2）设无穷远处电势为零，类比地球和物体间的万有引力而具有的引力势能，电子运动的轨道半径从 a 变化到 b（b > a），电子电势能的变化量 ΔE_p（    ）

A．ke² （\(\frac{1}{{{a^2}}}\) − \(\frac{1}{{{b^2}}}\)）           B．ke²（\(\frac{1}{a}\) − \(\frac{1}{b}\)）              C．ke²（\(\frac{1}{b}\) − \(\frac{1}{a}\)）              D．ke（\(\frac{1}{b}\) − \(\frac{1}{a}\)）

【答案】

1．1，①，①

2．

3．（1）D                （2）B

 

2．动物世界里的趣味物理

“洞天察地，万物之理”，我们生活在物理的世界里，很多现象背后都蕴含着丰富的物理知识。请尝试运用学过的物理知识来解释下面这些动物世界里的有趣现象。

 

1．（多选）有一种小虫能用坚硬的背部和地面碰撞，使身体竖直离地弹起，将身体内积蓄的能量转化为机械能。已知小虫质量为 m，其猛然收缩体内背纵肌，使重心迅速下降 d，与地面碰撞后离地最大高度为 h，且 d ≪ h。重力加速度为 g。小虫（    ）

A．离地弹起时动能为 mgh                        B．体内积蓄的能量为 mgd

C．与地面碰撞的作用力大于 mg               D．与地面碰撞的作用力小于 mg

 

2．小薛同学养了一只很调皮的小花猫。有一天他观察到猫在花园里竖直起跳。小猫先自下而上、再自上而下地两次经过一楼书房窗户的上、下边沿，猫经过窗户的总时间为 0.60 s，窗户高度为 1.2 m。则猫在下降过程中经过窗户的平均速率 \(\bar v\) = _______m/s，猫上升的最高点到窗户上边沿的高度差 Δh =_______m。（结果均保留 2 位有效数字）

 

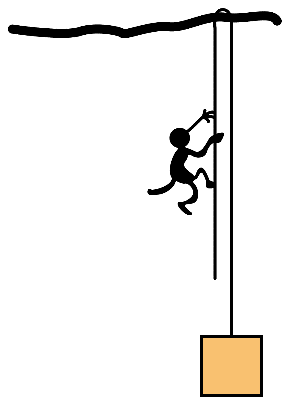3．如图，一质量为 8 kg 的猴子在空中抓着一根绳子沿绳向上爬，绳子的另一端牢牢系在一个质量为 12 kg 的箱子上，绳子质量不计，绳子与树干间摩擦不计。如果猴子能将箱子提离地面，设猴子的最小加速度为 a₁。一段时间后猴子体力不支，只能停止上爬而抓住绳子不放，设猴子的加速度为 a₂，则（    ）

A．a₁、a₂ 均竖直向下，| a₁∶a₂ | = 2∶3

B．a₁、a₂ 均竖直向上，| a₁∶a₂ | = 5∶2

C．a₁ 竖直向上，a₂ 竖直向下，| a₁∶a₂ | = 2∶5

D．a₁ 竖直向下，a₂ 竖直向上，| a₁∶a₂ | = 3∶2

 

4．（计算）研究表明侏罗纪时代的一种恐龙——暴龙的前肢特别短小，后肢长而强壮，善干套跑，但快速奔跑时可能有栽倒的危险，它的前肢太短无法帮助它缓冲重心的下落。假设一只暴龙质量为 m，在水平奔跑时突然栽倒，身体撞击地面前重心下落 h，身体和地面撞击过程用时为 t，在它和地面撞击期间身体同时在地面上滑行，地面和暴龙身体间的动摩擦因数为 μ。重力加速度为 g。求暴龙和地面撞击期间，暴龙在地面上滑行的水平加速度大小。

【答案】

1．AC

2．4.0，0.33

3．B

4．μ(\(\frac{{\sqrt {2gh} }}{t}\) + g)

 

3．光的现象及应用

人类对光的研究可以追溯到公元前 1000 多年，现代科技发展使人类对光现象的理解和应用不断深入。

 

1．如图所示，飞船 A 向正对自己飞来的飞船 B 发出一束激光，同时飞船 C 正向远方飞去，在同一参照系中测得的飞船 A、B、C 的速率已在图中标出。

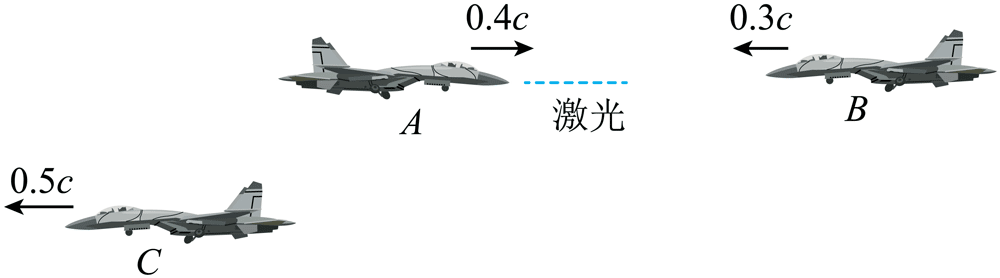
（1）（多选）设飞船 A、B、C 测得的激光速率分别为 v_A、v_B、v_C，则（    ）

A．v_A > v_B              B．v_A < v_B              C．v_A = v_B              D．v_B > v_C              E．v_B < v_C

F．v_B = v_C               G．v_A > v_C              H．v_A < v_C              I．v_A = v_C

（2）飞船 B 中的时钟记录飞船 B 中的宇航员锻炼了 5 min，在飞船 A 中观测该宇航员的锻炼时长为 t_A，则（      ）

A．t_A > 5 min                 B．t_A = 5 min                  C．t_A < 5 min

 

2．1950 年，艾森用空腔共振法来测量光速。实验中将微波输入圆柱形的空腔中，发生共振时空腔的圆周长与微波波长成正比，比例系数为 k。已知空腔直径为 d，发生共振时测得微波频率为 f，则光速 c =________。

 

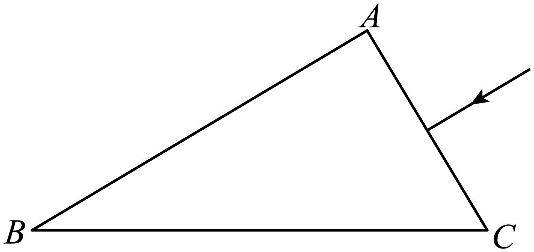3．直角棱镜的横截面如图所示，图中 ∠A = 90°，∠B = 30°，AC 边长为 10 cm。截面内一细束单色光线从棱镜 AC 边中点垂直射入，在 BC 边未观察到光线射出，在 AB 边观察到有光线射出，则光线在 AB 边的出射点到 B 点的距离为________cm。此棱镜的折射率 n 的取值范围为________。

 

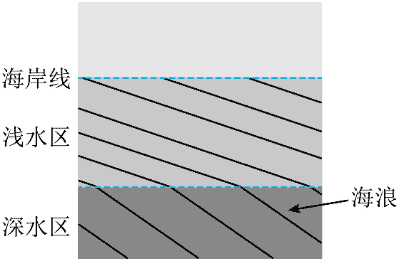4．海浪以 5.00 m/s 的速率与海岸线成 50.0° 角的方向涌向海滩，离岸边一定距离处海水深度突然变浅，导致海水在该处的速率减小为 3.5 m/s，传播方向也发生变化，如图所示。

（1）该现象为波的（    ）

A．反射    B．折射    C．干涉    D．衍射

（2）（简答）将该现象与光现象进行类比，分析并求出接近海岸处海浪运动方向与海岸线的夹角。（结果保留 3 位有效数字）

【答案】

1．（1）CFI            （2）A

2．\(\frac{{\pi df}}{k}\)

3．5.77（\(\frac{{10\sqrt 3 }}{3}\)），\(\frac{{2\sqrt 3 }}{3}\) ≤ n < 2

4．（1）B

（2）63.3°

【解析】

1．（1）根据爱因斯坦相对论，在任何参考系中，光速不变，即光速不随光源和观察者所在参考系的相对运动而改变，所以飞船 A、B、C 测得的激光速率都为 c。故选 CFI。

飞船 B 中的宇航员记录的时间为固有时，也是为最短，在其他参考系中记录的时间都比固有时长。故选 A。

2．由题可知  πd = kλ，而 c = λf，联立解得 c = \(\frac{{\pi df}}{k}\)。

3．光路如图所示。

垂直 AC 进入棱镜，到达 BC 的中点 D，发生全反射，到达 AB 边上的 E 点，如图由几何关系可知 BD = 10 cm

因此 BE = \(\frac{{{\rm{BD}}}}{{2\cos 30^\circ }}\) = \(\frac{{10\sqrt 3 }}{3}\) cm

由于在 BC 边发生全反射，入射角为 60°，因此 n₁ ≥ \(\frac{1}{{\sin 60^\circ }}\) = \(\frac{{2\sqrt 3 }}{3}\)

反射到 AB 边上，入射角为30°，光线能射出，因此 n₁ < \(\frac{1}{{\sin 30^\circ }}\) = 2

折射率的取值范围 \(\frac{{2\sqrt 3 }}{3}\) ≤ n < 2

4．（1）波从一种介质进入到另一种介质，传播方向发生改变的现象称为波的折射。故选 B。

（2）海浪（波）在深水区和浅水区的传播速度不同，可将深水区和水区视作两种介质，波由深水区进入浅水区后传插速度减小，传播方向也发生变化，这是波的折射现象。

波在深水区运动方向的入射角 θ₁ = 40°，设波在浅水区运动方向的折射角为 θ₂，类比光的折射定律：\(\frac{{\sin {\theta _1}}}{{\sin {\theta _2}}}\) = \(\frac{{{v_1}}}{{{v_2}}}\)，可得：sinθ₂ = \(\frac{{{v_2}\sin {\theta _1}}}{{{v_1}}}\) = \(\frac{{3.5 \times \sin 40^\circ }}{{5.0}}\) = 0.450，θ₂ = 26.7°，所以海浪运动方向与海岸线的夹角为 63.3°。

 

4．弹簧

弹簧是一种利用弹性来工作的机械零件，在科技生产和日常生活中有很多用处。

 

1．一个连续的正弦纵波由装在一根非常长的弹簧的一端的振源沿弹簧发出，波源频率为 20 Hz，弹簧上任一质点的振幅为 0.45 cm，任何时刻相邻两个质点分布最密的位置间距离为 24 cm。则该纵波的波速为________m/s，弹簧上任一质点经过 0.9 cm 的路程需用时________s。

 

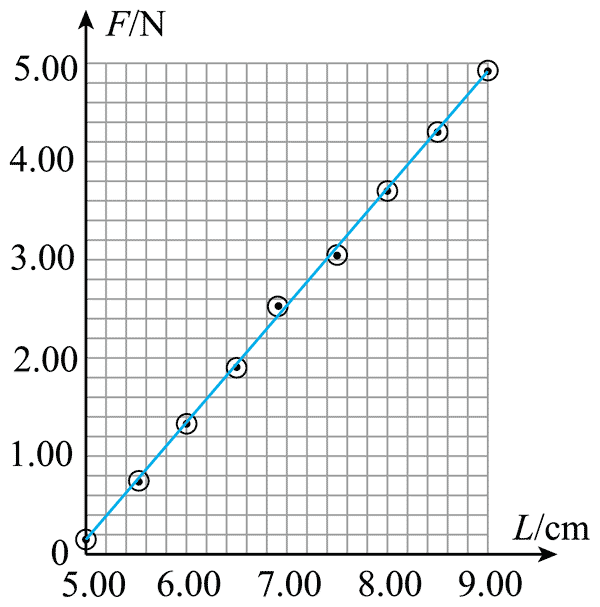
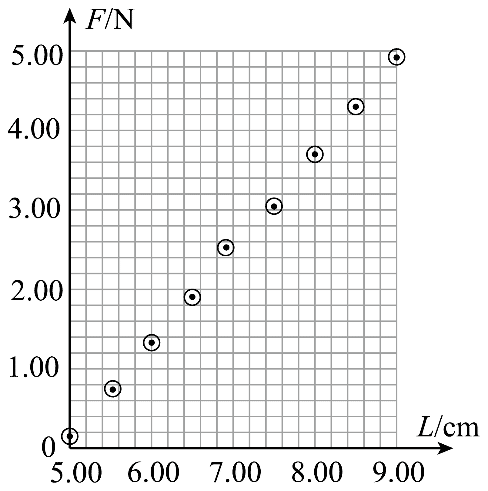2．某同学准备自制一个弹簧秤，他把弹簧上端悬挂在一固定力传感器上（力传感器测量方向已调整至竖直）。未悬挂重物前用刻度尺测得弹簧自然下垂的长度为 5.00 cm，力传感器读数为 0.196 N。在弹簧下端悬挂不同质量的重物，待稳定后用刻度尺测量弹簧的长度 L，并记录相应的力传感器读数 F。

（1）请根据 F–L 图中的数据点完成 F–L 图线；

（2）该弹簧的劲度系数 k =______N/m；（结果保留 3 位有效数字）

（3）用该弹簧秤测量一重物，力传感器读数为 3.00 N，则重物的质量 m = ________kg。（结果保留 3 位有效数字）

 

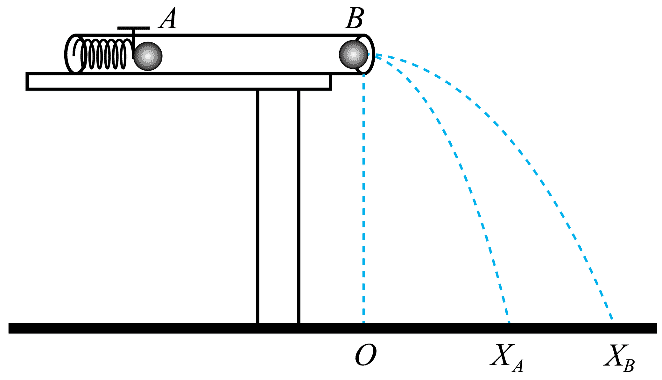3．用图示装置验证动量守恒定律。固定在水平桌面上、内壁光滑的直玻璃管内有一压紧的弹簧，此时弹簧长度为 L，其右侧放置一小球 A。右端管口放置一小球 B，将弹簧释放后球 A 向右运动，与弹簧分离，与球 B 发生碰撞后两球从管口飞出。图中 O 点是小球从管口飞出点在水平地面上的垂直投影，X_A 是球 A 落地点，X_B 是球 B 落地点。测量 O、X_A 两点间距离为 x_A，O、X_B 两点间距离为 x_B，管口到地面的高度为 h。重力加速度为 g。

（1）球 A、球 B 在空中飞行时间（    ）

A．相同                  B．不同

（2）球 B 飞出管口的初速度 v_B =________；（将两球视作质点）

（3）（不定项选择）撤去放置在管口的球 B，将弹簧压紧到长度仍为 L，右侧放置球 A，将弹簧释放，球 A 飞出管口后落地，落地点为 P（图中未标出）。为验证动量守恒定律，还需要测量的物理量有（      ）

A．球 A 的质量 m_A                    B．球 B 的质量 m_B

C．弹簧的原长 L₀                        D．OP 两点间距离 x_P

（4）若两球相碰前后的动量守恒，其表达式应满足________（用本题中测量的物理量符号表示）。

【答案】

1．4.8，0.025

2．（1）

（2）118（答案大于 120 或 小于115，不给分）

（3）0.286

3．（1）A

（2）x_B\(\sqrt {\frac{g}{{2h}}} \)

（3）ABD

（4）m_Ax_P = m_Ax_A + m_Bx_B

 

5．磁场的作用

近期太阳耀斑喷发高能粒子并产生辐射，在我国高纬度地区都观测到了美丽的极光，极光现象的产生与带电粒子在磁场中的运动有关。

 

1．地球上某地区的地磁场方向水平且指向正北方，通以恒定电流的长直导线水平放置在该地区，测得导线正上方某处磁感应强度恰好为零。该导线（    ）

A．南北向放置，电流方向由南向北

B．南北向放置，电流方向由北向南

C．东西向放置，电流方向由东向西

D．东西向放置，电流方向由西向东

 

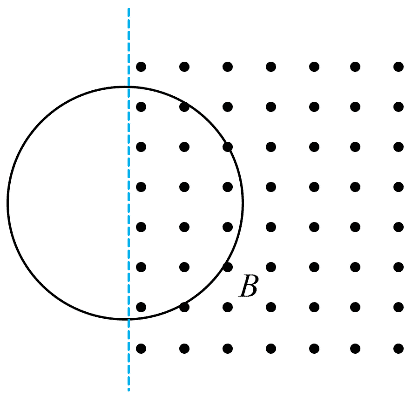2．一有界匀强磁场区域如图所示，质量为 m、电阻为 R、半径为 r的圆形线圈一半在磁场内，一半在磁场外。t = 0 时磁感应强度大小为 B₀，以后均匀减小至零，其随时间的变化率为一常数 k。线圈中产生感应电流，在磁场力作用下运动，不计重力影响。则 t = 0 时线圈的加速度 a 大小为________。线圈做匀速直线运动时回路中的电功率 P 可能为________。

 

3．如图，阴极射线管内有一束电子沿水平方向从左向右运动，整个装置处于竖直向下的匀强磁场中，磁感应强度大小为 B。其中一个电子的动量大小为 p。已知电子电量为 e，电子质量为 m。不计重力影响。

（1）该电子在磁场中的偏转方向为________。

（2）（计算）求该电子在磁场中运动的加速度大小；

（3）（计算）测得该电子穿出射线管时末速度方向与进入管内的初速度方向夹角的正弦值为 \(\frac{1}{a}\)，求管长 L。

【答案】

1．D

2．\(\frac{{{B_0}\pi k{r^3}}}{{mR}}\)，0 或 \(\frac{{{\pi ^2}{k^2}{r^4}}}{R}\)

3．（1）垂直纸面向外

（2）a = \(\frac{{Bpe}}{{{m^2}}}\)

（3）L = \(\frac{p}{{Bea}}\)

【解析】

3．（1）根据左手定则，四指指向电子运动方向的反方向，磁感线穿过手掌心，大拇指所指方向即为洛伦兹力方向，所以电子偏转方向为垂直纸面向外。

（2）电子在匀强磁场中受到洛伦兹力作用，f = Bvq = B \(\frac{p}{m}\) e，

根据牛顿第二定律：F_合 = ma，a = \(\frac{f}{m}\) = \(\frac{{Bpe}}{{{m^2}}}\)

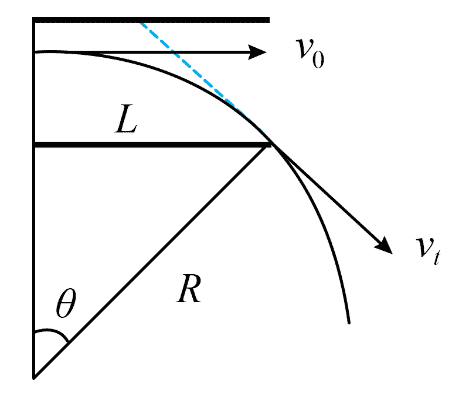（3）电子在匀强磁场中受洛伦兹力作用而做匀速圆周运动，在阴极射线管内走过一段圆弧，如图所示。洛伦兹力提供电子做匀速圆周运动所需的向心力：

f = Bve = m \(\frac{{{v^2}}}{R}\)

可得：R = \(\frac{{mv}}{{Be}}\) = \(\frac{p}{{Be}}\)

sinθ = \(\frac{L}{{R}}\)

将圆周半径 R 表达式代入，可得：L = \(\frac{p}{{Bea}}\)