2024年海南高考
- 下载
- 2024/7/7
- 151 次
- 398 K
1.神舟十七号载人飞船返回舱于 2024 年 4 月 30 日在东风着陆场成功着陆,在飞船返回至离地面十几公里时打开主伞飞船快速减速,返回舱速度大大减小,在减速过程中( )
A.返回舱处于超重状态 B.返回舱处于失重状态
C.主伞的拉力不做功 D.重力对返回舱做负功
【答案】
A
【解析】
AB.返回舱在减速过程中,加速度竖直向上,处于超重状态,故 A 正确,B 错误;
C.主伞的拉力与返回舱运动方向相反,对返回舱做负功,故 C 错误;
D.返回舱的重力与返回舱运动方向相同,重力对返回舱做正功,故 D 错误。
故选 A。
2.人工核反应 3014Si + 11H → X + 3015P 中的 X 是( )
A.中子 B.质子 C.电子 D.α 粒子
【答案】
A
【解析】
根据质量数守恒和电荷数守恒可知 X 的电荷数为 0,质量数为 1,则 X 是中子。
故选 A。
3.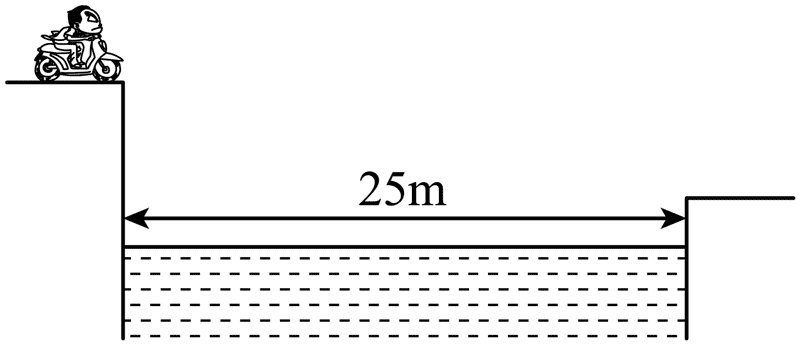 在跨越河流表演中,一人骑车以 25 m/s 的速度水平冲出平台,恰好跨越长 x = 25 m 的河流落在河对岸平台上,已知河流宽度 25 m,不计空气阻力,取 g = 10 m/s2,则两平台的高度差 h 为( )
在跨越河流表演中,一人骑车以 25 m/s 的速度水平冲出平台,恰好跨越长 x = 25 m 的河流落在河对岸平台上,已知河流宽度 25 m,不计空气阻力,取 g = 10 m/s2,则两平台的高度差 h 为( )
A.0.5 m B.5 m
C.10 m D.20 m
【答案】
B
【解析】
车做平抛运动,设运动时间为 t,
竖直方向 h =
水平方向 d= v0t
其中 d = 25 m、v0 = 25 m/s
解得 h = 5 m
故选 B。
4.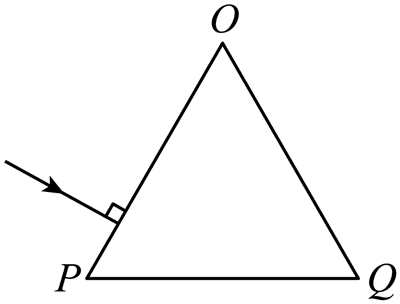 一正三角形 OPQ 玻璃砖,某束光线垂直于 OP 射入,恰好在 PQ 界面发生全反射,则玻璃砖的折射率( )
一正三角形 OPQ 玻璃砖,某束光线垂直于 OP 射入,恰好在 PQ 界面发生全反射,则玻璃砖的折射率( )
A.
【答案】
C
【解析】
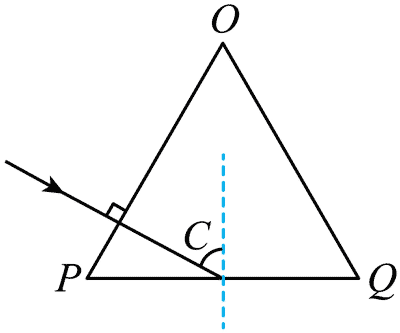 如图所示。根据几何关系可知光线在 PQ 界面的入射角为 C = 60°,
如图所示。根据几何关系可知光线在 PQ 界面的入射角为 C = 60°,
根据全反射的临界条件可得 sinC =
解得 n =
故选 C。
5.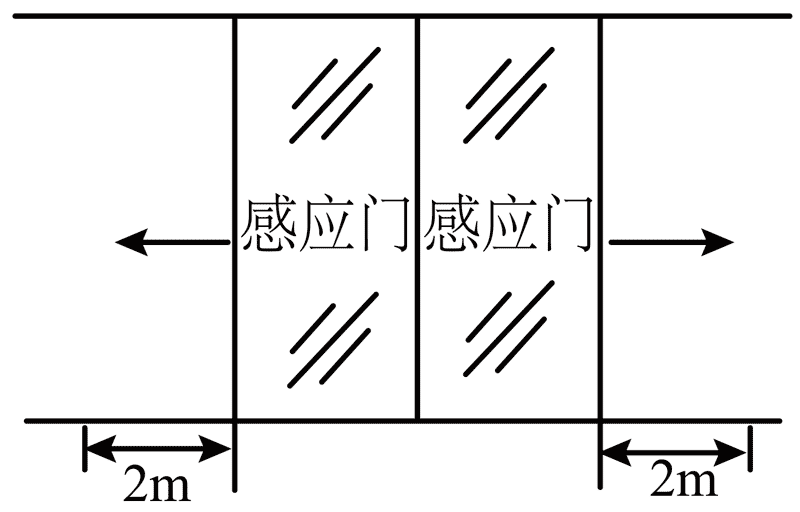 商场自动感应门如图所示,人走进时两扇门从静止开始同时向左右平移,经 4 s 恰好完全打开,两扇门移动距离均为 2 m,若门从静止开始以相同加速度大小先匀加速运动后匀减速运动,完全打开时速度恰好为 0,则加速度的大小为( )
商场自动感应门如图所示,人走进时两扇门从静止开始同时向左右平移,经 4 s 恰好完全打开,两扇门移动距离均为 2 m,若门从静止开始以相同加速度大小先匀加速运动后匀减速运动,完全打开时速度恰好为 0,则加速度的大小为( )
A.1.25 m/s2 B.1 m/s2
C.0.5 m/s2 D.0.25 m/s2
【答案】
C
6.嫦娥六号进入环月圆轨道,周期为 T,轨道高度与月球半径之比为 k,引力常量为 G,则月球的平均密度为( )
A.
【答案】
D
7.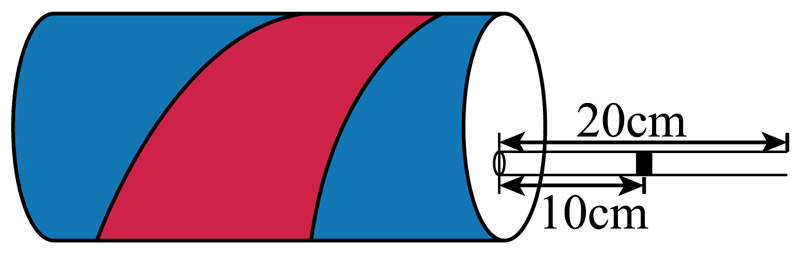 用铝制易拉罐制作温度计,一透明薄吸管里有一段油柱(长度不计)粗细均匀,吸管与罐密封性良好,罐内气体可视为理想气体,已知罐体积为 330 cm3,薄吸管底面积 0.5 cm2,罐外吸管总长度为 20 cm,当温度为 27℃ 时,油柱离罐口 10 cm,不考虑大气压强变化,下列说法正确的是( )
用铝制易拉罐制作温度计,一透明薄吸管里有一段油柱(长度不计)粗细均匀,吸管与罐密封性良好,罐内气体可视为理想气体,已知罐体积为 330 cm3,薄吸管底面积 0.5 cm2,罐外吸管总长度为 20 cm,当温度为 27℃ 时,油柱离罐口 10 cm,不考虑大气压强变化,下列说法正确的是( )
A.若在吸管上标注等差温度值,则刻度左密右疏
B.该装置所测温度不高于 31.5℃
C.该装置所测温度不低于 23.5℃
D.其他条件不变,缓慢把吸管拉出来一点,则油柱离罐口距离增大
【答案】
B
8.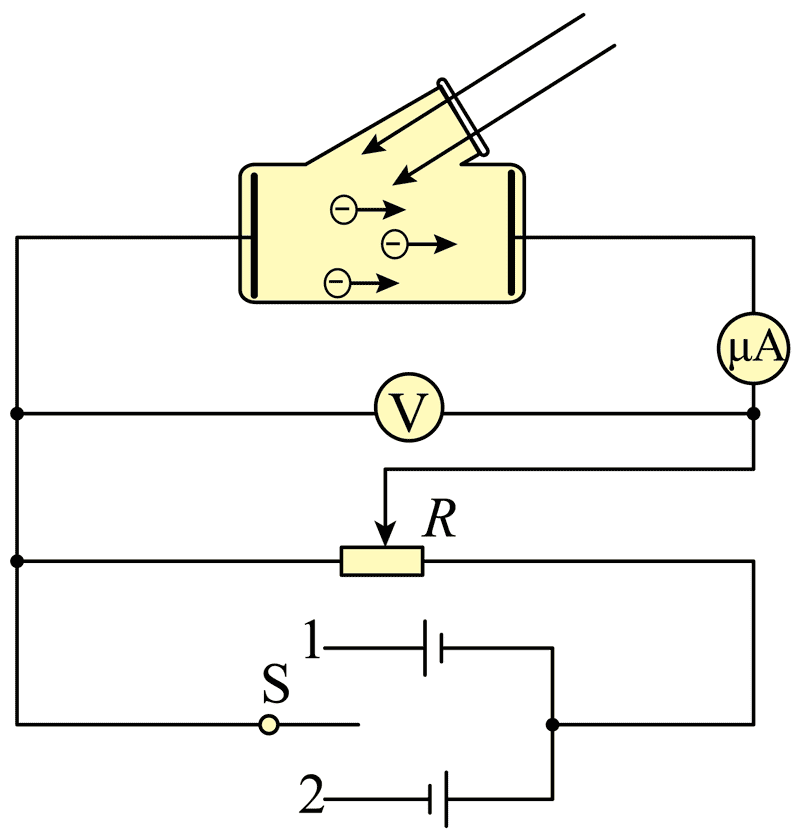 利用如图所示的装置研究光电效应,闭合单刀双掷开关 S1,用频率为 ν1 的光照射光电管,调节滑动变阻器,使电流表的示数刚好为 0,此时电压表的示数为 U1,已知电子电荷量为 e,普朗克常量为 h,下列说法正确的是( )
利用如图所示的装置研究光电效应,闭合单刀双掷开关 S1,用频率为 ν1 的光照射光电管,调节滑动变阻器,使电流表的示数刚好为 0,此时电压表的示数为 U1,已知电子电荷量为 e,普朗克常量为 h,下列说法正确的是( )
A.其他条件不变,增大光强,电压表示数增大
B.改用比 ν1 更大频率的光照射,调整电流表的示数为零,此时电压表示数仍为 U
C.其他条件不变,使开关接 S2,电流表示数仍为零
D.光电管阴极材料的截止频率 νc = ν1 –
【答案】
D
【解析】
A.当开关 S 接 1 时,由爱因斯坦光电效应方程 eU = hν1 − W0,故其他条件不变时,增大光强,电压表的示数不变,故 A 错误;
B.若改用比 ν1 更大频率的光照射时,调整电流表的示数为零,而金属的逸出功不变,故遏止电压变大,即此时电压表示数大于 U,故 B 错误;
C.其他条件不变时,使开关 S 接 2,此时 hν1 > W0,可发生光电效应,故电流表示数不为零,故 C 错误;
D.根据爱因斯坦光电效应方程 eU1 = hν1 − W0,其中 W0 = hνc。联立解得光电管阴极材料的截止频率为 νc = ν1 –
故选 D。
9.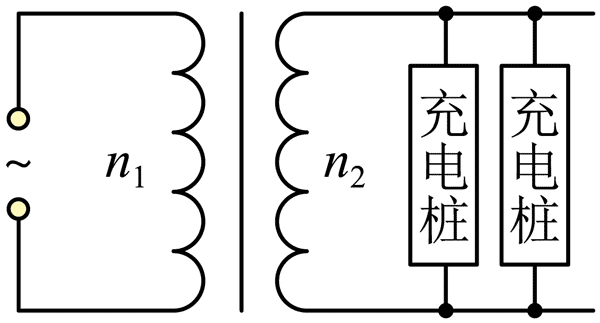 电动汽车充电站变压器输入电压为 10 kV,输出电压为 220 V,每个充电桩输入电流 16 A,设原副线圈匝数分别为 n1、n2,输入正弦交流的频率为 50 Hz,则下列说法正确的是( )
电动汽车充电站变压器输入电压为 10 kV,输出电压为 220 V,每个充电桩输入电流 16 A,设原副线圈匝数分别为 n1、n2,输入正弦交流的频率为 50 Hz,则下列说法正确的是( )
A.交流电的周期为 0.02 s
B.原副线圈匝数比 n1∶n2 = 11∶500
C.输出的最大电压为 220 V
D.若 10 台充电桩同时使用,输入功率为 35.2 kW
【答案】
AD
10.一歌手在湖边唱歌,歌声通过空气和水传到距其 2 km 的湖对岸,空气中的声速为 340 m/s,水中声速为 1450 m/s,歌声可视为频率为 400 Hz 的声波,则下列说法正确的是( )
A.在水中传播频率会改变
B.由空气和水传到湖对岸的时间差约为 4.5 s
C.在空气中波长为 0.85 m
D.在水中的波长为 5 m
【答案】
BC
11.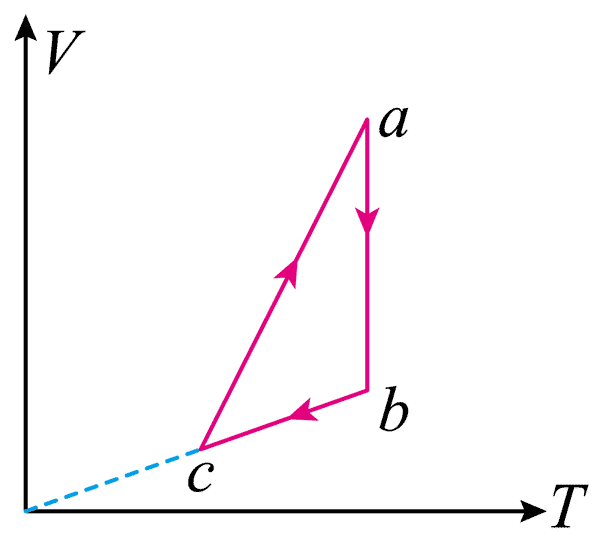 一定质量的理想气体从状态 a 开始经 ab、bc、ca 三个过程回到原状态,已知 ab 垂直于 T 轴,bc 延长线过 O 点,下列说法正确的是( )
一定质量的理想气体从状态 a 开始经 ab、bc、ca 三个过程回到原状态,已知 ab 垂直于 T 轴,bc 延长线过 O 点,下列说法正确的是( )
A.be 过程外界对气体做功 B.ca 过程气体压强不变
C.ab 过程气体放出热量 D.ca 过程气体内能减小
【答案】
AC
12.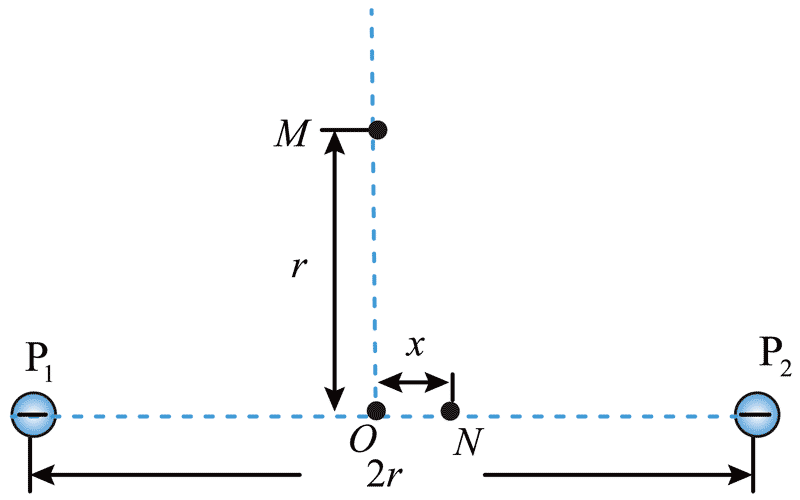 真空中有两个点电荷,电荷量均为 − q(q ≥ 0),固定于相距为 2r 的 P1、P2 两点,O 是 P1P2 连线的中点,M 点在 P1P2 连线的中垂线上,距离 O 点为 r,N 点在 P1P2 连线上,距离 O 点为 x(x ≪ r),已知静电力常量为 k,则下列说法正确的是( )
真空中有两个点电荷,电荷量均为 − q(q ≥ 0),固定于相距为 2r 的 P1、P2 两点,O 是 P1P2 连线的中点,M 点在 P1P2 连线的中垂线上,距离 O 点为 r,N 点在 P1P2 连线上,距离 O 点为 x(x ≪ r),已知静电力常量为 k,则下列说法正确的是( )
A.P1P2 中垂线上电场强度最大的点到 O 点的距离为
B.P1P2 中垂线上电场强度的最大值为
C.在 M 点放入一电子,从静止释放,电子的加速度一直减小
D.在 N 点放入一电子,从静止释放,电子的运动可视为简谐运动
【答案】
CD
13.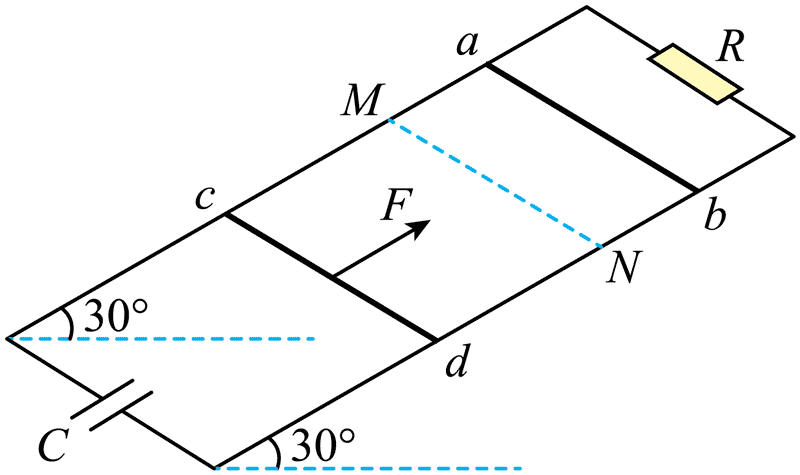 两根足够长的导轨由上下段电阻不计,光滑的金属导轨组成,在 M、N 两点绝缘连接,M、N 等高,间距 L = 1 m,连接处平滑。导轨平面与水平面夹角为 30°,导轨两端分别连接一个阻值 R = 0.02 Ω 的电阻和 C = 1 F 的电容器,整个装置处于 B = 0.2 T 的垂直导轨平面斜向上的匀强磁场中,两根导体棒 ab、cd 分别放在 MN 两侧,质量分为 m1 = 0.8 kg,m2 = 0.4 kg,ab 棒电阻为 0.08 Ω,cd 棒的电阻不计,将 ab 由静止释放,同时 cd 从距离 MN 为 x0 = 4.32 m 处在一个大小 F = 4.64 N,方向沿导轨平面向上的力作用下由静止开始运动,两棒恰好在 M、N 处发生弹性碰撞,碰撞前瞬间撤去 F,已知碰前瞬间 ab 的速度为 4.5 m/s,g = 10 m/s2( )
两根足够长的导轨由上下段电阻不计,光滑的金属导轨组成,在 M、N 两点绝缘连接,M、N 等高,间距 L = 1 m,连接处平滑。导轨平面与水平面夹角为 30°,导轨两端分别连接一个阻值 R = 0.02 Ω 的电阻和 C = 1 F 的电容器,整个装置处于 B = 0.2 T 的垂直导轨平面斜向上的匀强磁场中,两根导体棒 ab、cd 分别放在 MN 两侧,质量分为 m1 = 0.8 kg,m2 = 0.4 kg,ab 棒电阻为 0.08 Ω,cd 棒的电阻不计,将 ab 由静止释放,同时 cd 从距离 MN 为 x0 = 4.32 m 处在一个大小 F = 4.64 N,方向沿导轨平面向上的力作用下由静止开始运动,两棒恰好在 M、N 处发生弹性碰撞,碰撞前瞬间撤去 F,已知碰前瞬间 ab 的速度为 4.5 m/s,g = 10 m/s2( )
A.ab 从释放到第一次碰撞前所用时间为 1.44 s
B.ab 从释放到第一次碰撞前,R 上消耗的焦耳热为 0.78 J
C.两棒第一次碰撞后瞬间,ab 的速度大小为 6.3 m/s
D.两棒第一次碰撞后瞬间,cd 的速度大小为 8.4 m/s
【答案】
BD
14.水平圆盘上紧贴边缘放置一密度均匀的小圆柱体,如图(1)所示,图(2)为俯视图,测得圆盘直径 D = 42.02 cm,圆柱体质量 m = 30.0 g,圆盘绕过盘心 O1 的竖直轴匀速转动,转动时小圆柱体相对圆盘静止。
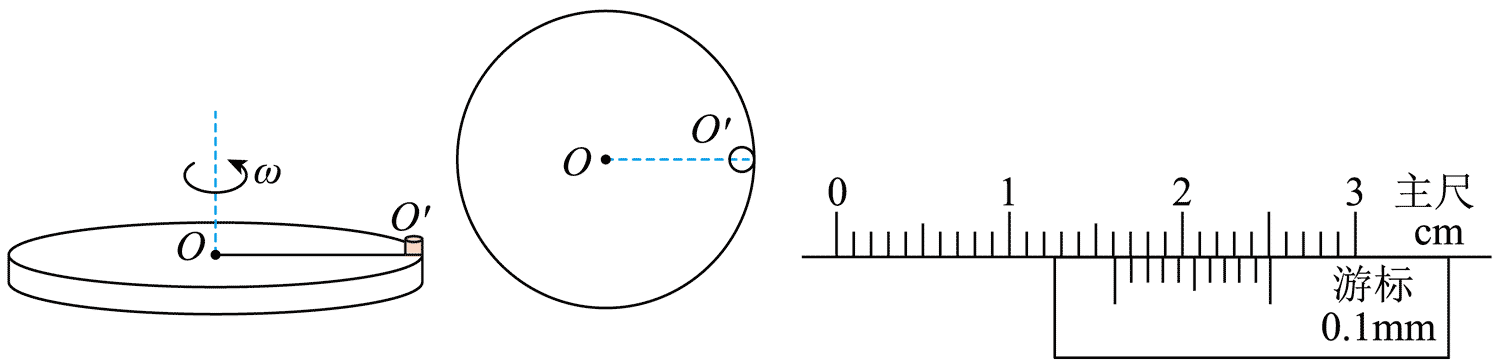
为了研究小圆柱体做匀速圆周运动时所需要的向心力情况,某同学设计了如下实验步骤:
(1)用秒表测圆盘转动 10 周所用的时间 t = 62.8 s,则圆盘转动的角速度 ω =_____rad/s(π 取 3.14)
(2)用游标卡尺测量小圆柱体不同位置的直径,某次测量的示数如图(3)所示,该读数 d =_____mm,多次测量后,得到平均值恰好与 d 相等。
(3)写出小圆柱体所需向心力表达式 F =_____(用 D、m、ω、d 表示),其大小为_____N(保留2位有效数字)
【答案】
(1)1
(2)16.2
(3)
14.为验证两个互成角度的力的合成规律,某组同学用两个弹簧测力计、橡皮条、轻质小圆环、木板、刻度尺、白纸、铅笔、细线和图钉等器材,按照如下实验步骤完成实验:
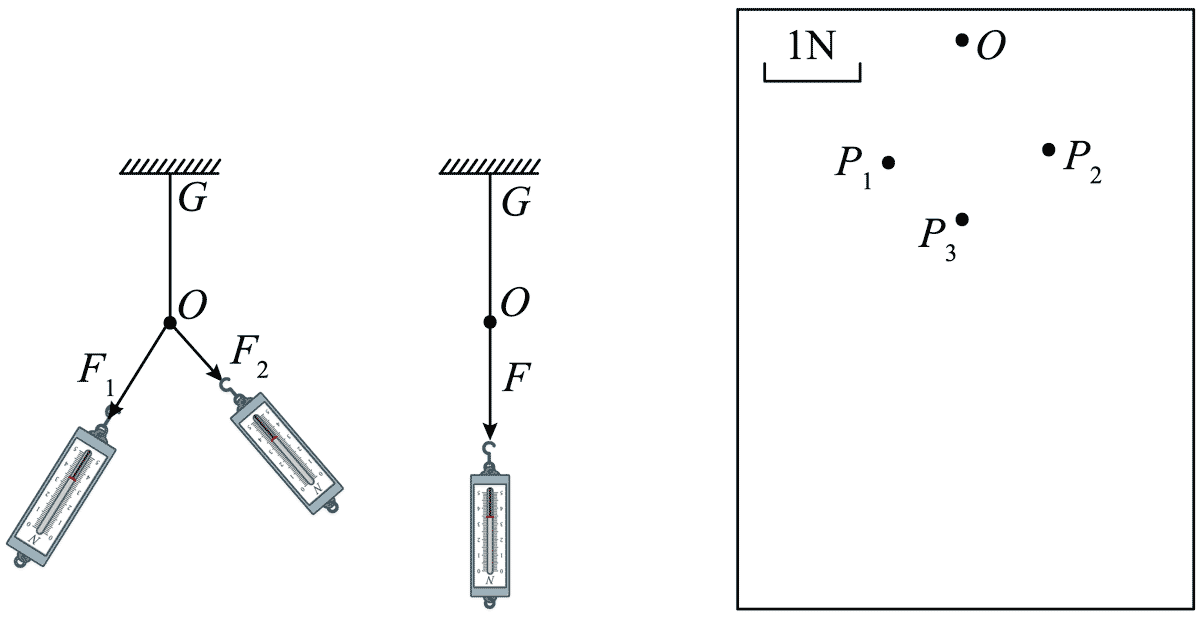
(Ⅰ)用图钉将白纸固定在水平木板上;
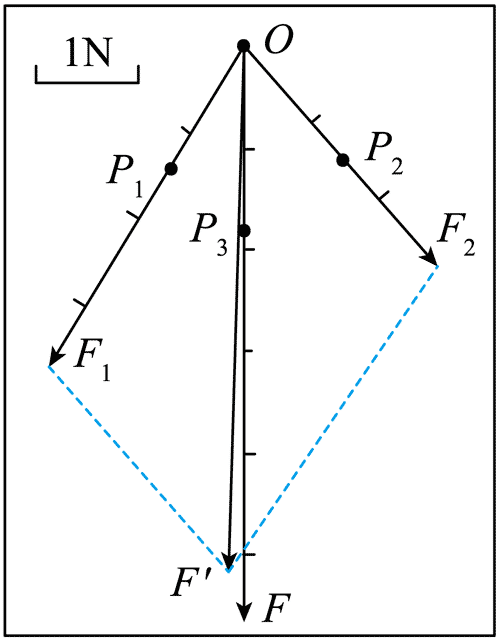
(Ⅱ)如图(1)(2)所示,橡皮条的一端固定在木板上的 G 点,另一端连接轻质小圆环,将两细线系在小圆环上,细线另一端系在弹簧测力计上,用两个弹簧测力计共同拉动小圆环到某位置,并标记圆环的圆心位置为 O 点,拉力 F1 和 F2 的方向分别过 P1 和 P2 点,大小分别为 F1 = 3.60 N、F2 = 2.90 N;拉力 F1 和 F2,改用一个弹簧测力计拉动小圆环,使其圆心到 O 点,在拉力 F 的方向上标记 P3 点,拉力的大小为 F = 5.60 N。请完成下列问题:
(1)在图(2)中按照给定的标度画出 F1、F2 和 F 的图示,然后按平行四边形定则画出 F1、F2 的合力 F′。
(2)比较 F 和 F′,写出可能产生误差的两点原因_________________________。
【答案】
(1)
(2)①没有做到弹簧秤、细绳、橡皮条都与木板平行;②读数时没有正视弹簧测力计
15.用如图 a 所示的电路观察电容器的充放电现象,实验器材有电源 E、电容器 C、电压表、电流表、电流传感器、计算机、定值电阻 R、单刀双掷开关 S1、开关 S2、导线若干。
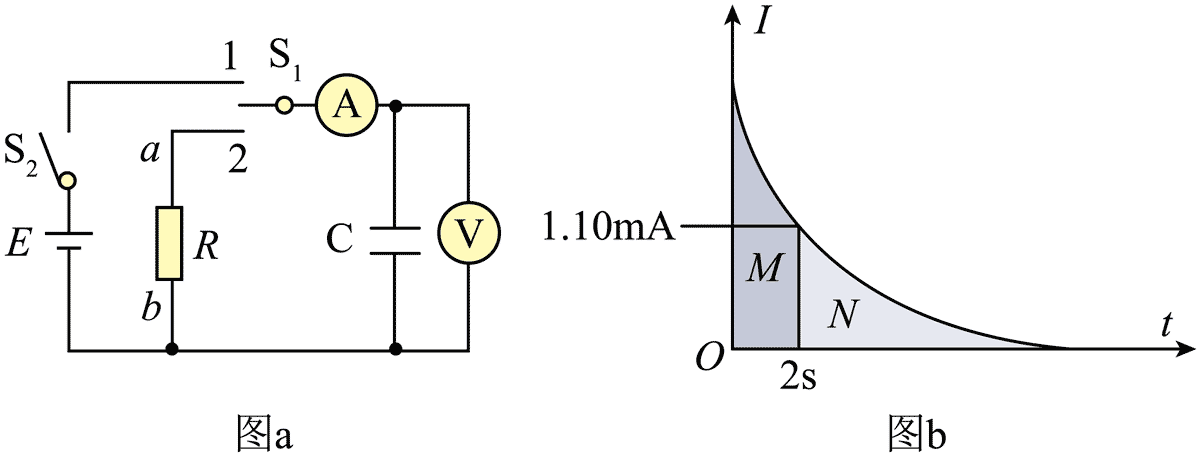
(1)闭合开关 S2,将 S1 接 1,电压表示数增大,最后稳定在 12.3 V。在此过程中,电流表的示数_____(填选项标号)
A.一直稳定在某一数值
B.先增大,后逐渐减小为零
C.先增大,后稳定在某一非零数值
(2)先后断开开关 S2、S1,将电流表更换成电流传感器,再将 S1 接 2,此时通过定值电阻 R 的电流方向_____(选填“a→b”或“b→a”),通过传感器将电流信息传入计算机,画出电流随时间变化的 I – t 图像,如图 b,t = 2 s 时 I = 1.10 mA,图中 M、N 区域面积比为 8∶7,可求出 R =_____kΩ(保留 2 位有效数字)。
【答案】
(1)B
(2)a→b,5.2
【解析】
(1)电容器充电过程中,当电路刚接通后,电流表示数从 0 增大某一最大值,后随着电容器的不断充电,电路中的充电电流在减小,当充电结束电路稳定后,此时电路相当于开路,电流为 0。故选 B。
(2)根据电路图可知充电结束后电容器上极板带正电,将 S1 接 2,电容器放电,此时通过定值电阻 R 的电流方向 a→b;
t = 2 s 时 I = 1.10 mA 可知此时电容器两端的电压为 U2 = IR
电容器开始放电前两端电压为 12.3 V,根据 I – t 图像与横轴围成的面积表示放电量可得 0 ~ 2 s 间的放电量为 Q1 = ΔU⋅C = (12.3 − 1.10×10−3×R)C
2 s 后到放电结束间放电量为 Q2 =ΔUʹ⋅C = 1.10×10−3⋅RC
根据题意 Q1∶Q2 = 8∶7,解得 R = 5.2 kΩ
16.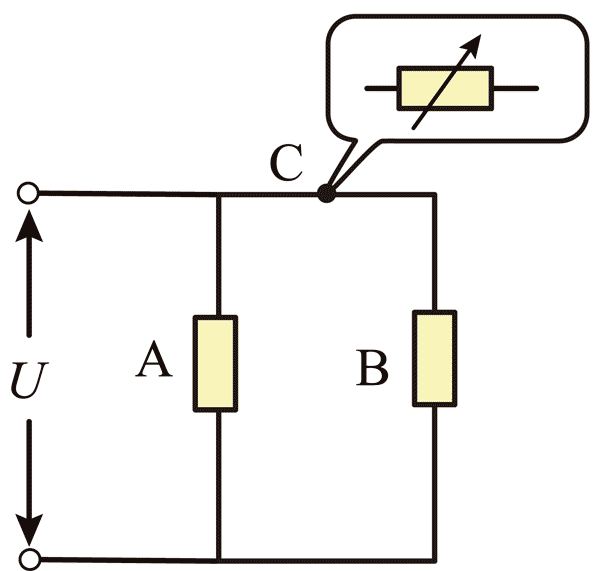 虚接是常见的电路故障,如图所示,电热器 A 与电热器 B 并联。电路中的 C 处由于某种原因形成了虚接,造成了该处接触电阻 0 ~ 240 Ω 之间不稳定变化,可等效为电阻 RC,已知 MN 两端电压 U = 220 V,A 与 B 的电阻 RA = RB = 24 Ω,求:
虚接是常见的电路故障,如图所示,电热器 A 与电热器 B 并联。电路中的 C 处由于某种原因形成了虚接,造成了该处接触电阻 0 ~ 240 Ω 之间不稳定变化,可等效为电阻 RC,已知 MN 两端电压 U = 220 V,A 与 B 的电阻 RA = RB = 24 Ω,求:
(1)MN 间电阻 R 的变化范围;
(2)当 RC = 240 Ω,电热器 B 消耗的功率(保留 3 位有效数字)
【答案】
(1)12 Ω ≤ R ≤ 22 Ω
(2)16.7 W
17.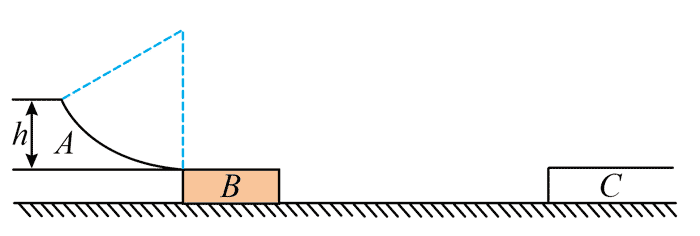 某游乐项目装置简化如图,A 为固定在地面上的光滑圆弧形滑梯,半径 R = 10 m,滑梯顶点 a 与滑梯末端 b 的高度 h = 5 m,静止在光滑水平面上的滑板 B,紧靠滑梯的末端,并与其水平相切,滑板质量 M = 25 kg,一质量为 m = 50 kg 的游客,从 a 点由静止开始下滑,在 b 点滑上滑板,当滑板右端运动到与其上表面等高平台的边缘时,游客恰好滑上平台,并在平台上滑行 s = 16 m 停下。游客视为质点,其与滑板及平台表面之间的动摩擦系数均为 μ = 0.2,忽略空气阻力,重力加速度 g = 10 m/s2,求:
某游乐项目装置简化如图,A 为固定在地面上的光滑圆弧形滑梯,半径 R = 10 m,滑梯顶点 a 与滑梯末端 b 的高度 h = 5 m,静止在光滑水平面上的滑板 B,紧靠滑梯的末端,并与其水平相切,滑板质量 M = 25 kg,一质量为 m = 50 kg 的游客,从 a 点由静止开始下滑,在 b 点滑上滑板,当滑板右端运动到与其上表面等高平台的边缘时,游客恰好滑上平台,并在平台上滑行 s = 16 m 停下。游客视为质点,其与滑板及平台表面之间的动摩擦系数均为 μ = 0.2,忽略空气阻力,重力加速度 g = 10 m/s2,求:
(1)游客滑到 b 点时对滑梯的压力的大小;
(2)滑板的长度 L。
【答案】
(1)1000 N
(2)7 m
18.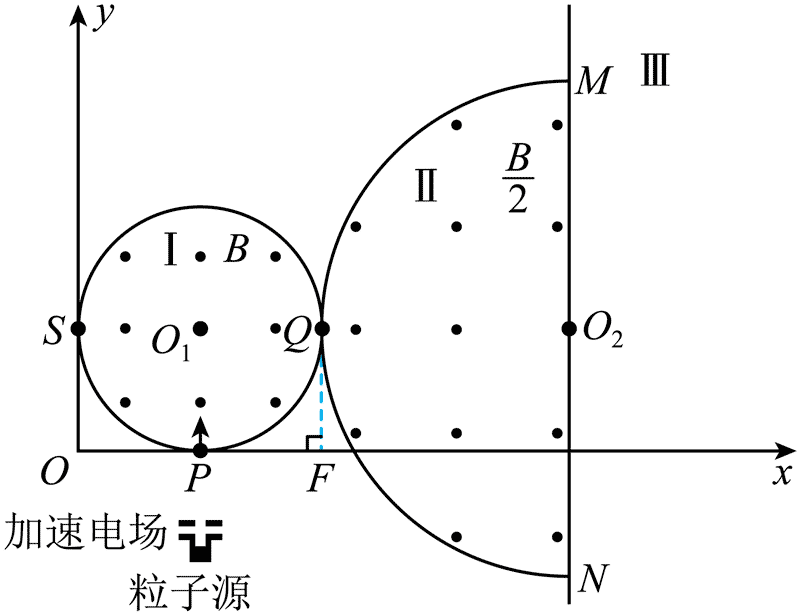 如图,在 xOy 坐标系中有三个区域,圆形区域 Ⅰ 分别与 x 轴和 y 轴相切于 P 点和 S 点。半圆形区域 Ⅱ 的半径是区域 Ⅰ 半径的 2 倍。区域 Ⅰ、Ⅱ 的圆心 O1、O2 连线与 x 轴平行,半圆与圆相切于 Q 点,QF 垂直于 x 轴,半圆的直径 MN 所在的直线右侧为区域 Ⅲ。区域 Ⅰ、Ⅱ 分别有磁感应强度大小为 B、
如图,在 xOy 坐标系中有三个区域,圆形区域 Ⅰ 分别与 x 轴和 y 轴相切于 P 点和 S 点。半圆形区域 Ⅱ 的半径是区域 Ⅰ 半径的 2 倍。区域 Ⅰ、Ⅱ 的圆心 O1、O2 连线与 x 轴平行,半圆与圆相切于 Q 点,QF 垂直于 x 轴,半圆的直径 MN 所在的直线右侧为区域 Ⅲ。区域 Ⅰ、Ⅱ 分别有磁感应强度大小为 B、
(1)求加速电场两板间的电压 U 和区域 Ⅰ 的半径 R;
(2)在能射入区域 Ⅲ 的粒子中,某粒子在区域 Ⅱ 中运动的时间最短,求该粒子在区域 Ⅰ 和区域 Ⅱ 中运动的总时间 t;
(3)在区域 Ⅲ 加入匀强磁场和匀强电场,磁感应强度大小为 B,方向垂直纸面向里,电场强度的大小 E = Bv0,方向沿 x 轴正方向。此后,粒子源中某粒子经区域 Ⅰ、Ⅱ 射入区域 Ⅲ,进入区域 Ⅲ 时速度方向与 y 轴负方向的夹角成 74° 角。当粒子动能最大时,求粒子的速度大小及所在的位置到 y 轴的距离。(sin37° = 0.6,sin53° = 0.8)
【答案】
(1)U =
(2)
(3)vm = 2.6v0,
【解析】
(1)根据动能定理得 qU = mv02
解得 U =
粒子进入区域 I 做匀速圆周运动,根据题意某粒子从 P 点射入区域 Ⅰ,并从 Q 点射入区域 Ⅱ,故可知此时粒子的运动轨迹半径与区域 Ⅰ 的半径 R 相等,粒子在磁场中运动洛伦兹力提供向心力 Bqv0 = m
解得 R =
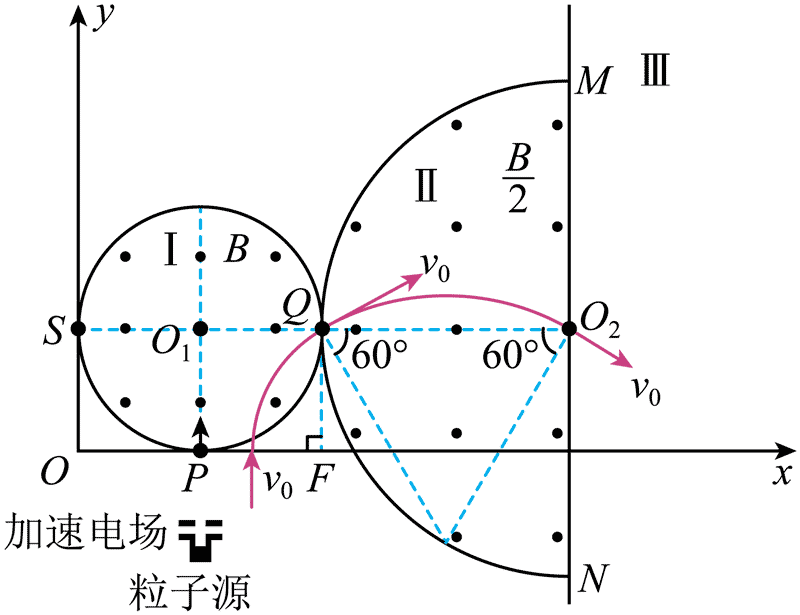 (2)如图,要使粒子在区域 Ⅱ 中运动的时间最短,轨迹所对应的圆心角最小,可知在区域 Ⅱ 中运动的圆弧所对的弦长最短,即此时最短弦长为区域 Ⅱ 的磁场圆半径 2R,根据几何知识可得此时在区域 Ⅱ 和区域 Ⅰ 中运动的轨迹所对应的圆心角都为 60°,粒子在两区域磁场中运动周期分别为
(2)如图,要使粒子在区域 Ⅱ 中运动的时间最短,轨迹所对应的圆心角最小,可知在区域 Ⅱ 中运动的圆弧所对的弦长最短,即此时最短弦长为区域 Ⅱ 的磁场圆半径 2R,根据几何知识可得此时在区域 Ⅱ 和区域 Ⅰ 中运动的轨迹所对应的圆心角都为 60°,粒子在两区域磁场中运动周期分别为
…………
(3)如图,将速度 v0 分解为沿 y 轴正方向的速度 v0 及速度 vʹ,因为 E = Bv0 可得 Eq = Bqv0,故可知沿y轴正方向的速度 v0 产生的洛伦兹力与电场力平衡,粒子同时受到另一方向的洛伦兹力 Bqvʹ,故粒子沿 y 正方向做旋进运动,根据角度可知
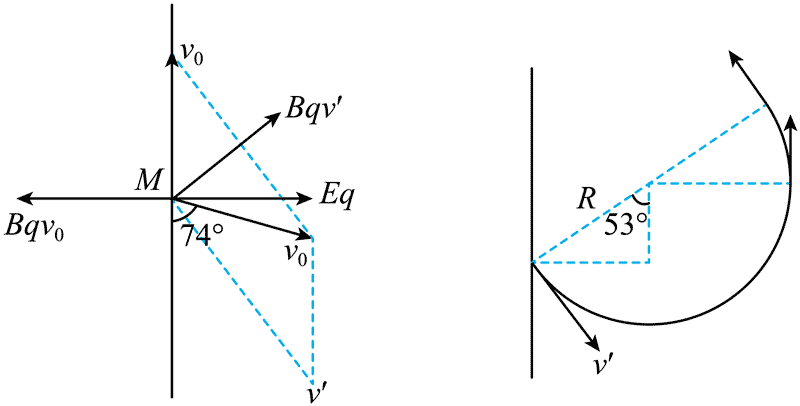
…………
2006 - 2025,推荐分辨率 1024*768 以上,推荐浏览器 Chrome、Edge 等现代浏览器,截止 2021 年 12 月 5 日的访问次数:1872 万 9823。 站长邮箱
