1．2024 年是中国航天大年，神舟十八号、嫦娥六号等已陆续飞天，部分航天器装载了具有抗干扰性强的核电池。已知 ⁹⁰₃₈Sr 衰变为 ⁹⁰₃₉Y 的半衰期约为 29 年；²³⁸₉₄Pu 衰变为 ²³⁴₉₂U 的半衰期约87年。现用相同数目的 ⁹⁰₃₈Sr 和 ²³⁸₉₄Pu 各做一块核电池，下列说法正确的是（     ）

A．⁹⁰₃₈Sr 衰变为 ⁹⁰₃₉Y 时产生 α 粒子

B．²³⁸₉₄Pu 衰变为 ²³⁴₉₂U 时产生 β 粒子

C．50 年后，剩余的 ⁹⁰₃₈Sr 数目大于 ²³⁸₉₄Pu 的数目

D．87 年后，剩余的 ⁹⁰₃₈Sr 数目小于 ²³⁸₉₄Pu 的数目

【答案】

D

【解析】

A．根据质量数守恒和电荷数守恒可知 ⁹⁰₃₈Sr 衰变为 ⁹⁰₃₉Y 时产生电子，即 β 粒子，故A错误；

B．根据质量数守恒和电荷数守恒可知 ²³⁸₉₄Pu 衰变为 ²³⁴₉₂U 时产生 ⁴₂He，即 α 粒子，故 B 错误；

CD．根据题意可知 ²³⁸₉₄Pu 的半衰期大于 ⁹⁰₃₈Sr 的半衰期，现用相同数目的 ⁹⁰₃₈Sr 和 ²³⁸₉₄Pu 各做一块核电池，经过相同的时间，⁹⁰₃₈Sr 经过的半衰期的次数多，所以 ⁹⁰₃₈Sr 数目小于 ²³⁸₉₄Pu 的数目，故 D 正确，C 错误。

故选 D。

 

2．如图所示，国产人形机器人“天工”能平稳通过斜坡。若它可以在倾角不大于 30° 的斜坡上稳定地站立和行走，且最大静摩擦力等于滑动摩擦力，则它的脚和斜面间的动摩擦因数不能小于（    ）

A．\(\frac{1}{2}\)             B．\(\frac{{\sqrt 3 }}{3}\)          C．\(\frac{{\sqrt 2 }}{2}\)          D．\(\frac{{\sqrt 3 }}{2}\)

【答案】

B

【解析】

根据题意可知机器人“天工”它可以在倾角不大于 30° 的斜坡上稳定地站立和行走，对“天工”分析有

mgsin30° ≤ μmgcos30°

可得 μ ≥ \(\frac{{\sqrt 3 }}{3}\)

故选 B。

 

3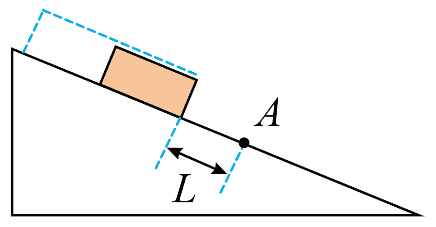．如图所示，固定的光滑斜面上有一木板，其下端与斜面上 A 点距离为 L。木板由静止释放，若木板长度 L，通过 A 点的时间间隔为 Δt₁；若木板长度为 2L，通过 A 点的时间间隔为 Δt₂。Δt₂∶Δt₁ 为（    ）

A．（\({\sqrt 3 }\) − 1）∶（\({\sqrt 2 }\) − 1）

B．（\({\sqrt 3 }\) − \({\sqrt 2 }\)）∶（\({\sqrt 2 }\) − 1）

C．（\({\sqrt 3 }\) + 1）∶（\({\sqrt 2 }\) + 1）

D．（\({\sqrt 3 }\) + \({\sqrt 2 }\)）∶（\({\sqrt 2 }\) + 1）

【答案】

A

【解析】

木板在斜面上运动时，木板的加速度不变，设加速度为 a，木板从静止释放到下端到达 A 点的过程，根据运动学公式有 L = \(\frac{1}{2}\)at₀²；

木板从静止释放到上端到达 A 点的过程，当木板长度为 L 时，有 2L = \(\frac{1}{2}\)at₁²；

当木板长度为 2L 时，有 3L = \(\frac{1}{2}\)at₂²；

又 Δt₁ = t₁ – t₀，Δt₂ = t₂ – t₀

联立解得 Δt₂∶Δt₁ = （\({\sqrt 3 }\) − 1）∶（\({\sqrt 2 }\) − 1）

故选 A。

 

4．检测球形滚珠直径是否合格的装置如图甲所示，将标准滚珠 a 与待测滚珠 b、c 放置在两块平板玻璃之间，用单色平行光垂直照射平板玻璃，形成如图乙所示的干涉条纹。若待测滚珠与标准滚珠的直径相等为合格，下列说法正确的是（    ）

A．滚珠 b、c 均合格

B．滚珠 b、c 均不合格

C．滚珠 b 合格，滚珠 c 不合格

D．滚珠 b 不合格，滚珠 c 合格

【答案】

C

【解析】

单色平行光垂直照射平板玻璃，上、下玻璃上表面的反射光在上玻璃上表面发生干涉，形成干涉条纹，光程差为两块玻璃距离的两倍，根据光的干涉知识可知，同一条干涉条纹位置处光的波程差相等，即滚珠a的直径与滚珠b的直径相等，即滚珠b合格，不同的干涉条纹位置处光的波程差不同，则滚珠a的直径与滚珠c的直径不相等，即滚珠c不合格。

故选C。

 

5．“鹊桥二号”中继星环绕月球运行，其 24 小时椭圆轨道的半长轴为 a。已知地球同步卫星的轨道半径为 r，则月球与地球质量之比可表示为（    ）

A．\(\sqrt {\frac{{{r^3}}}{{{a^3}}}} \)              B．\(\sqrt {\frac{{{a^3}}}{{{r^3}}}} \)              C．\({\frac{{{r^3}}}{{{a^3}}}}\)            D．\({\frac{{{a^3}}}{{{r^3}}}}\)

【答案】

D

 

6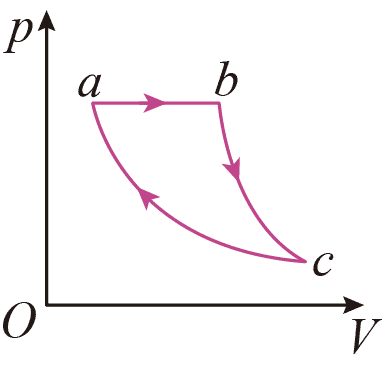．一定质量理想气体经历如图所示的循环过程，a→b 过程是等压过程，b→c 过程中气体与外界无热量交换，c→a 过程是等温过程。下列说法正确的是（    ）

A．a→b 过程，气体从外界吸收的热量全部用于对外做功

B．b→c 过程，气体对外做功，内能增加

C．a→b→c 过程，气体从外界吸收的热量全部用于对外做功

D．a→b 过程，气体从外界吸收的热量等于 c→a 过程放出的热量

【答案】

C

【解析】

A．a→b过程压强不变，是等压变化且体积增大，气体对外做功 W < 0，由盖-吕萨克定律可知 T_b > T_a

即内能增大，ΔU_ab > 0，根据热力学第一定律 ΔU = Q + W 可知 a→b 过程，气体从外界吸收的热量一部分用于对外做功，另一部分用于增加内能，A 错误；

B．方法一：b→c 过程中气体与外界无热量交换，即 Q_bc = 0

又由气体体积增大可知 W_bc < 0，由热力学第一定律 ΔU = Q + W 可知气体内能减少。

方法二：c→a 过程为等温过程，所以 T_c = T_a。

结合 T_b > T_a 分析可知 T_b > T_c。

所以 b 到 c 过程气体的内能减少。故 B 错误；

C．c→a 过程为等温过程，可知 T_c > T_a，ΔU_ac = 0。

根据热力学第一定律可知 a→b→c 过程，气体从外界吸收的热量全部用于对外做功，C 正确；

D．根据热力学第一定律结合上述解析可知：a→b→c→a 一整个热力学循环过程 ΔU = 0，整个过程气体对外做功，因此热力学第一定律可得

ΔU = Q_ab − Q_ca – W =0

故 a→b 过程气体从外界吸收的热量 Q_ab 不等于 c→a 过程放出的热量 – Q_ca，D错误。

故选 C。

 

7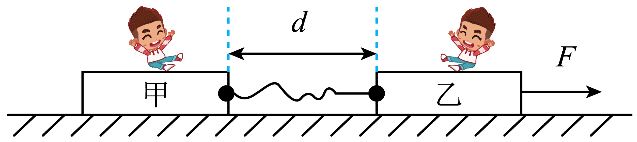．如图所示，质量均为 m 的甲、乙两同学，分别坐在水平放置的轻木板上，木板通过一根原长为 l 的轻质弹性绳连接，连接点等高且间距为 d（d < l）。两木板与地面间动摩擦因数均为 μ，弹性绳劲度系数为 k，被拉伸时弹性势能 E = \(\frac{1}{2}\)kx²（x 为绳的伸长量）。现用水平力 F 缓慢拉动乙所坐木板，直至甲所坐木板刚要离开原位置，此过程中两人与所坐木板保持相对静止，k 保持不变，最大静摩擦力等于滑动摩擦力，重力加速度大小为 g，则 F 所做的功等于（    ）

A．\(\frac{{{{(\mu mg)}^2}}}{{2k}}\) + μmg(l − d)                B．\(\frac{{3{{(\mu mg)}^2}}}{{2k}}\) + μmg(l − d)

C．\(\frac{{3{{(\mu mg)}^2}}}{{2k}}\) + 2μmg(l − d)            D．\(\frac{{{{(\mu mg)}^2}}}{{2k}}\) + 2μmg(l − d)

【答案】

B

 

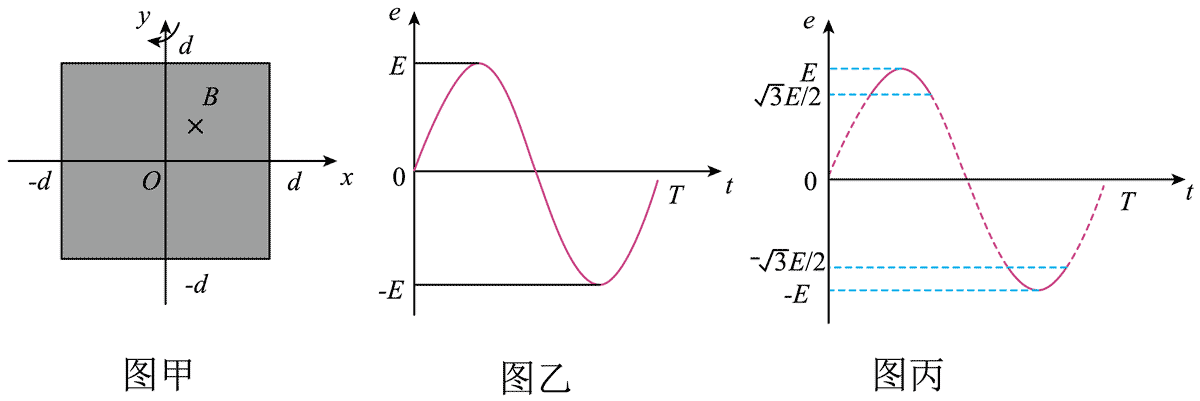
8．如图甲所示，在 − d ≤ x ≤ d，− d ≤ y ≤ d 的区域中存在垂直 Oxy 平面向里、磁感应强度大小为 B 的匀强磁场（用阴影表示磁场的区域），边长为 2d 的正方形线圈与磁场边界重合。线圈以 y 轴为转轴匀速转动时，线圈中产生的交变电动势如图乙所示。若仅磁场的区域发生了变化，线圈中产生的电动势变为图丙所示实线部分，则变化后磁场的区域可能为（    ）

【答案】

C

【解析】

根据题意可知，磁场区域变化前线圈产生的感应电动势为 e = Esinωt

由题图丙可知，磁场区域变化后，当 Esinωt = \(\frac{{\sqrt 3 }}{2}\) E 时，线圈的侧边开始切割磁感线，即当线圈旋转 \(\frac{\pi }{3}\) 时开始切割磁感线，由几何关系可知磁场区域平行于 x 轴的边长变为

dʹ = 2dcos\(\frac{\pi }{3}\) = d

C 正确。

故选 C。

 

9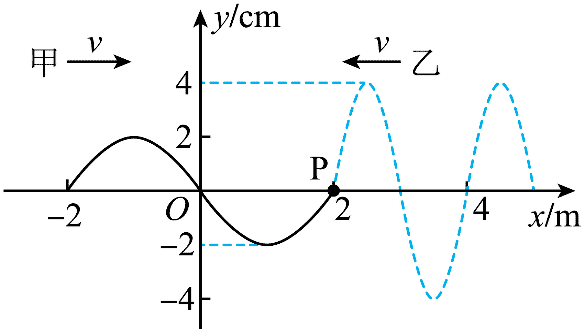．甲、乙两列简谐横波在同一均匀介质中沿 x 轴相向传播，波速均为 2 m/s。t = 0 时刻二者在 x = 2 m 处相遇，波形图如图所示。关于平衡位置在 x = 2 m 处的质点 P，下列说法正确的是（    ）

A．t = 0.5 s 时，P 偏离平衡位置的位移为 0

B．t = 0.5 s 时，P 偏离平衡位置的位移为 – 2 cm

C．t = 1.0 s 时，P 向 y 轴正方向运动

D．t = 1.0 s 时，P 向 y 轴负方向运动

【答案】

BC

【解析】

AB．在 0.5 s 内，甲、乙两列波传播的距离均为

Δx = vΔt = 2×0.5 m = 1 m

根据波形平移法可知，t = 0.5 s 时，x = 1 m 处甲波的波谷刚好传到 P 处，x = 3 m 处乙波的平衡位置振动刚好传到 P 处，根据叠加原理可知，t = 0.5 s 时，P 偏离平衡位置的位移为 – 2 cm，故 A 错误，B 正确；

CD．在 1.0 s 内，甲、乙两列波传播的距离均为

Δxʹ = vΔtʹ = 2×1.0 m = 2 m

根据波形平移法可知，t = 1.0 s 时，x = 0 甲波的平衡位置振动刚好传到 P 处，x = 4 m 处乙波的平衡位置振动刚好传到 P 处，且此时两列波的振动都向y轴正方向运动，根据叠加原理可知，t = 1.0 s 时，P 向 y 轴正方向运动，故 C 正确，D 错误。

故选 BC。

 

10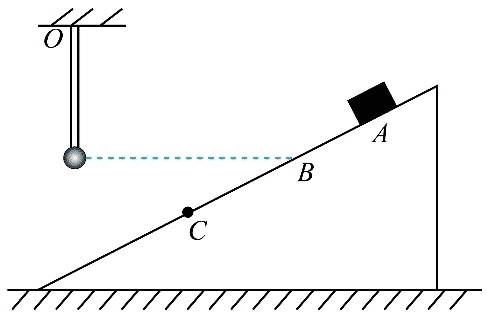．如图所示，带电量为 + q 的小球被绝缘棒固定在 O 点，右侧有固定在水平面上、倾角为 30° 的光滑绝缘斜面。质量为 m、带电量为 + q 的小滑块从斜面上 A 点由静止释放，滑到与小球等高的 B 点时加速度为零，滑到 C 点时速度为零。已知 AC 间的距离为 s，重力加速度大小为 g，静电力常量为 k，下列说法正确的是（    ）

A．OB 的距离 l = \(\sqrt {\frac{{\sqrt 3 k{q^2}}}{{mg}}} \)

B．OB的距离 l = \(\sqrt {\frac{{\sqrt 3 k{q^2}}}{{3mg}}} \)

C．从 A 到 C，静电力对小滑块做功 W = − mgs

D．AC之间的电势差 U_AC = − \(\frac{{mgs}}{{2q}}\)

【答案】

AD

【解析】

AB．由题意知小滑块在 B 点处的加速度为零，则根据受力分析有沿斜面方向

mgsin30° = \(\frac{{k{q^2}}}{{{l^2}}}\) cos30°

解得 l = \(\sqrt {\frac{{\sqrt 3 k{q^2}}}{{mg}}} \)

A 正确，B 错误；

C．因为滑到 C 点时速度为零，小滑块从 A 到 C 的过程，静电力对小滑块做的功为 W，根据动能定理有

W + mgs sin30° = 0

解得 W = − \(\frac{{mgs}}{{2}}\)

故 C 错误；

D．根据电势差与电场强度的关系可知 AC 之间的电势差

U_AC = \(\frac{W}{q}\) = − \(\frac{{mgs}}{{2q}}\)

故 D 正确。

故选 AD。

 

11．如图所示，两条相同的半圆弧形光滑金属导轨固定在水平桌面上，其所在平面竖直且平行，导轨最高点到水平桌面的距离等于半径，最低点的连线 OO' 与导轨所在竖直面垂直。空间充满竖直向下的匀强磁场（图中未画出），导轨左端由导线连接。现将具有一定质量和电阻的金属棒 MN 平行 OO' 放置在导轨图示位置，由静止释放。MN 运动过程中始终平行于 OO' 且与两导轨接触良好，不考虑自感影响，下列说法正确的是（    ）

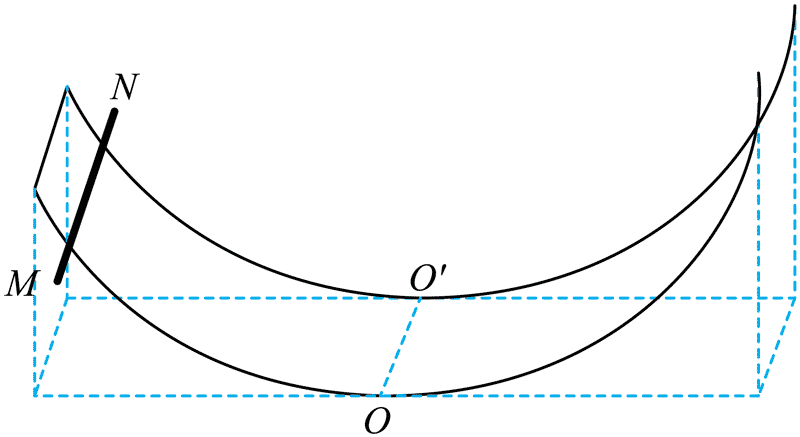
A．MN 最终一定静止于 OO' 位置

B．MN 运动过程中安培力始终做负功

C．从释放到第一次到达 OO' 位置过程中，MN 的速率一直在增大

D．从释放到第一次到达 OO' 位置过程中，MN 中电流方向由 M 到 N

【答案】

ABD

【解析】

A．由于金属棒 MN 运动过程切割磁感线产生感应电动势，回路有感应电流，产生焦耳热，金属棒 MN 的机械能不断减小，由于金属导轨光滑，所以经过多次往返运动，MN 最终一定静止于 OO' 位置，故 A 正确；

B．当金属棒 MN 向右运动，根据右手定则可知，MN 中电流方向由 M 到 N，根据左手定则，可知金属棒 MN 受到的安培力水平向左，则安培力做负功；当金属棒 MN 向左运动，根据右手定则可知，MN 中电流方向由 N 到 M，根据左手定则，可知金属棒 MN 受到的安培力水平向右，则安培力做负功；可知 MN 运动过程中安培力始终做负功，故 B 正确；

C．金属棒 MN 从释放到第一次到达 OO' 位置过程中，由于在 OO' 位置重力沿切线方向的分力为 0，可知在到达 OO' 位置之前的位置，重力沿切线方向的分力已经小于安培力沿切线方向的分力，金属棒 MN 已经做减速运动，故 C 错误；

D．从释放到第一次到达 OO' 位置过程中，根据右手定则可知，MN 中电流方向由 M 到 N，故 D 正确。

故选 ABD。

 

12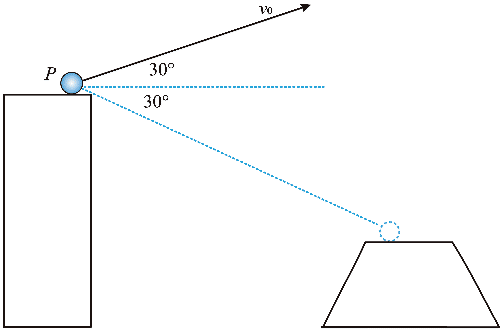．如图所示，工程队向峡谷对岸平台抛射重物，初速度 v₀ 大小为 20 m/s，与水平方向的夹角为 30°，抛出点 P 和落点 Q 的连线与水平方向夹角为 30°，重力加速度大小取 10 m/s²，忽略空气阻力。重物在此运动过程中，下列说法正确的是（    ）

A．运动时间为 2\(\sqrt 3 \) s

B．落地速度与水平方向夹角为 60°

C．重物离 PQ 连线的最远距离为 10 m

D．轨迹最高点与落点的高度差为 45 m

【答案】

BD

 

13．在第四次“天宫课堂”中，航天员演示了动量守恒实验。受此启发，某同学使用如图甲所示的装置进行了碰撞实验，气垫导轨两端分别安装 a、b 两个位移传感器，a 测量滑块 A 与它的距离 x_A，b 测量滑块 B 与它的距离 x_B。部分实验步骤如下：

①测量两个滑块的质量，分别为 200.0 g 和 400.0 g；

②接通气源，调整气垫导轨水平；

③拨动两滑块，使 A、B 均向右运动；

④导出传感器记录的数据，绘制 x_A、x_B 随时间变化的图像，分别如图乙、图丙所示。

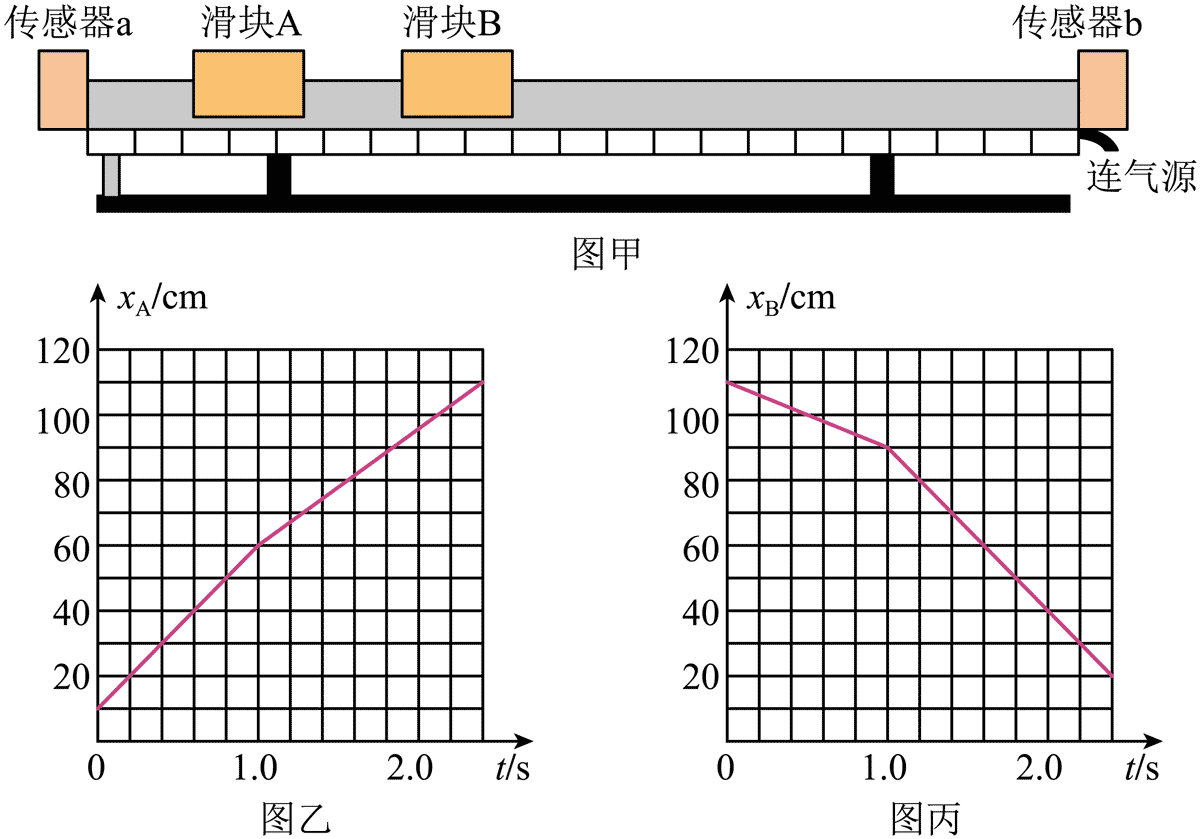
回答以下问题：

（1）从图像可知两滑块在 t = _________s 时发生碰撞；

（2）滑块 B 碰撞前的速度大小 v = _____________m/s（保留 2 位有效数字）；

（3）通过分析，得出质量为 200.0 g 的滑块是________（填“A”或“B”）。

【答案】

（1）1.0

（2）0.20

（3）B

 

14．某学习小组对两种型号铅笔芯的电阻率进行测量。实验器材如下：

学生电源（输出电压 0 ~ 16 V）

滑动变阻器（最大阻值 10 Ω，额定电流 2 A）；

电压表 V（量程 3 V，内阻未知）；

电流表 A（量程 3 A，内阻未知）；

待测铅笔芯 R（X 型号、Y 型号）；

游标卡尺，螺旋测微器，开关 S，单刀双掷开关 K，导线若干。

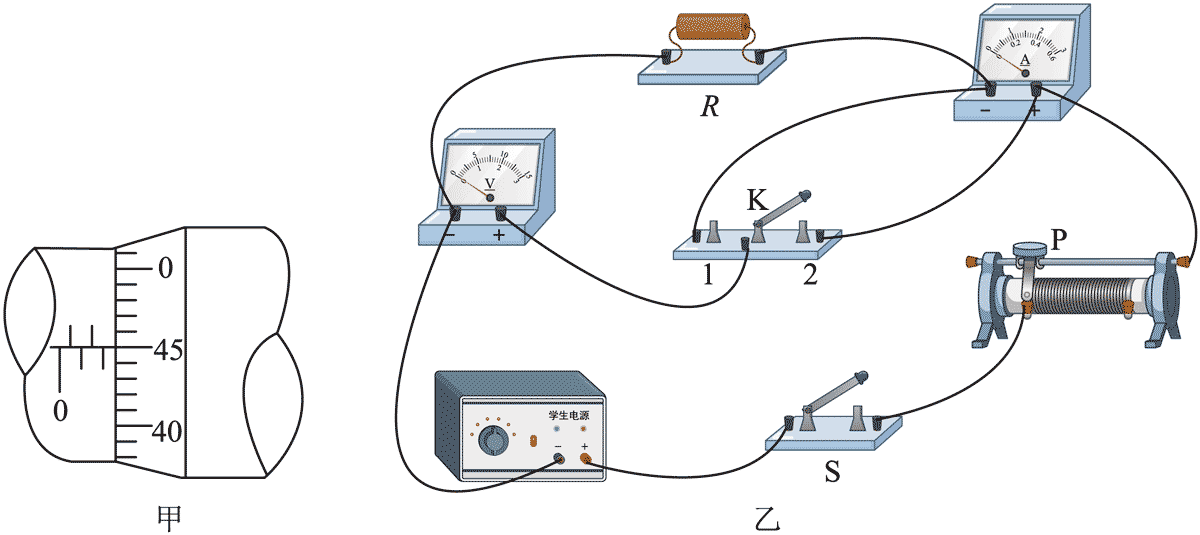
回答以下问题：

（1）使用螺旋测微器测量铅笔芯直径，某次测量结果如图甲所示，该读数为_______mm；

（2）把待测铅笔芯接入图乙所示电路，闭合开关 S 后，将滑动变阻器滑片由最右端向左调节到合适位置，将单刀双掷开关 K 分别掷到 1、2 端，观察到电压表示数变化比电流表示数变化更明显，则测量铅笔芯电阻时应将 K 掷到________（填“1”或“2”）端；

（3）正确连接电路，得到 Y 型号铅笔芯 I – U 图像如图丙所示，求得电阻 R_Y = ______Ω（保留 3 位有效数字）；采用同样方法得到X型号铅笔芯的电阻为 1.70 Ω；

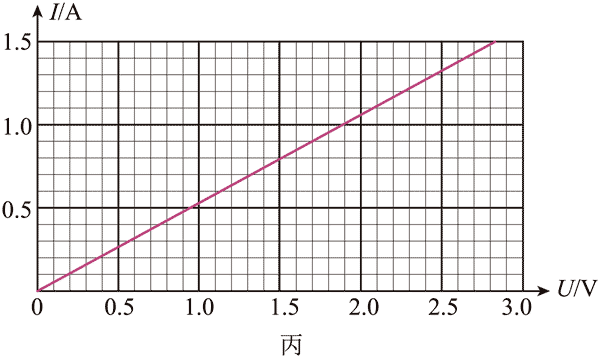
（4）使用游标卡尺测得 X、Y 型号铅笔芯的长度分别为 40.68 mm、60.78 mm，使用螺旋测微器测得 X、Y 型号铅笔芯直径近似相等，则X型号铅笔芯的电阻率______（填“大于”或“小于”）Y 型号铅笔芯的电阻率。

【答案】

（1）2.450

（2）1

（3）1.91

（4）大于

 

15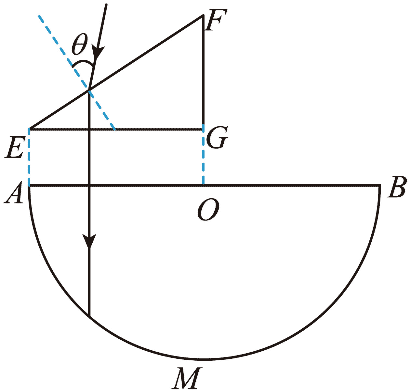．某光学组件横截面如图所示，半圆形玻璃砖圆心为 O 点，半径为 R；直角三棱镜 FG 边的延长线过 O 点，EG 边平行于 AB 边且长度等于 R，∠FEG = 30°。横截面所在平面内，单色光线以 θ 角入射到 EF 边发生折射，折射光线垂直 EG 边射出。已知玻璃砖和三棱镜对该单色光的折射率均为 1.5。

（1）求 sinθ；

（2）以 θ 角入射的单色光线，若第一次到达半圆弧 AMB 可以发生全反射，求光线在 EF 上入射点 D（图中未标出）到 E 点距离的范围。

【答案】

（1）sinθ = 0.75

（2）0 < x ≤ \(\frac{{2\sqrt 3 }}{9}\) R

 

16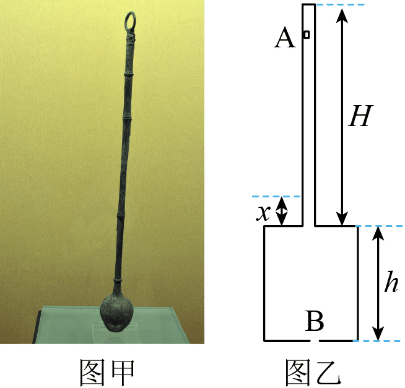．图甲为战国时期青铜汲酒器，根据其原理制作了由中空圆柱形长柄和储液罐组成的汲液器，如图乙所示。长柄顶部封闭，横截面积 S₁ = 1.0 cm²，长度 H = 100.0 cm，侧壁有一小孔 A。储液罐的横截面积 S₂ = 90.0 cm²，高度 h = 20.0 cm，罐底有一小孔 B。汲液时，将汲液器竖直浸入液体，液体从孔 B 进入，空气由孔 A 排出；当内外液面相平时，长柄浸入液面部分的长度为 x；堵住孔 A，缓慢地将汲液器竖直提出液面，储液罐内刚好储满液体。已知液体密度 ρ = 1.0×10³ kg/m³，重力加速度大小 g = 10 m/s²，大气压 p₀ = 1.0×10⁵ Pa。整个过程温度保持不变，空气可视为理想气体，忽略器壁厚度。

（1）求 x；

（2）松开孔 A，从外界进入压强为 p₀、体积为 V 的空气，使满储液罐中液体缓缓流出，堵住孔 A，稳定后罐中恰好剩余一半的液体，求 V。

【答案】

（1）x = 2 cm

（2）V = 8.92×10⁻⁴ m³

 

17．如图甲所示，质量为 M 的轨道静止在光滑水平面上，轨道水平部分的上表面粗糙，竖直半圆形部分的表面光滑，两部分在 P 点平滑连接，Q 为轨道的最高点。质量为 m 的小物块静置在轨道水平部分上，与水平轨道间的动摩擦因数为 μ，最大静摩擦力等于滑动摩擦力。已知轨道半圆形部分的半径 R = 0.4 m，重力加速度大小 g = 10 m/s²。

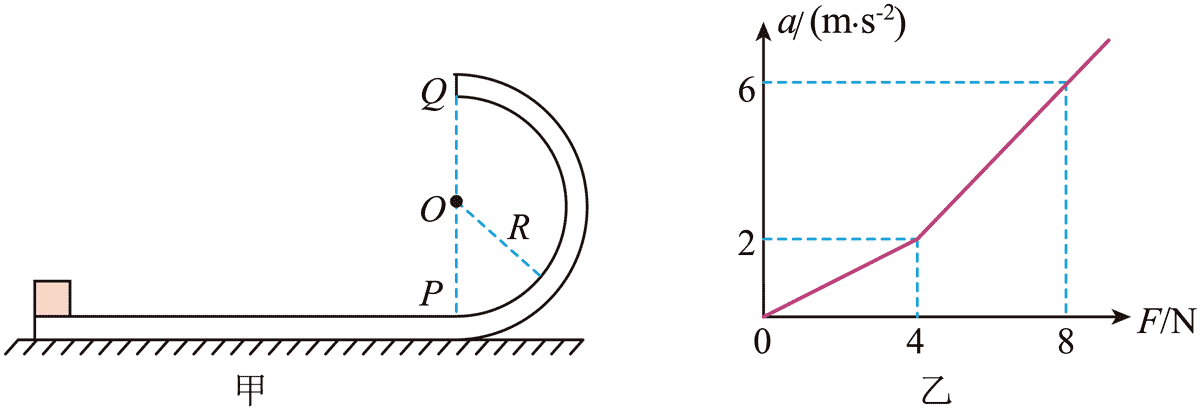
（1）若轨道固定，小物块以一定的初速度沿轨道运动到 Q 点时，受到轨道的弹力大小等于 3mg，求小物块在 Q 点的速度大小 v；

（2）若轨道不固定，给轨道施加水平向左的推力 F，小物块处在轨道水平部分时，轨道加速度 a 与 F 对应关系如图乙所示。

（ⅰ）求 μ 和 m；

（ⅱ）初始时，小物块静置在轨道最左端，给轨道施加水平向左的推力 F = 8 N，当小物块到 P 点时撤去 F，小物块从 Q 点离开轨道时相对地的速度大小为 7 m/s。求轨道水平部分的长度 L。

【答案】

（1）v = 4 m/s

（2）（ⅰ）m = 1 kg，μ = 0.2

（ⅱ）L = 4.5 m

 

18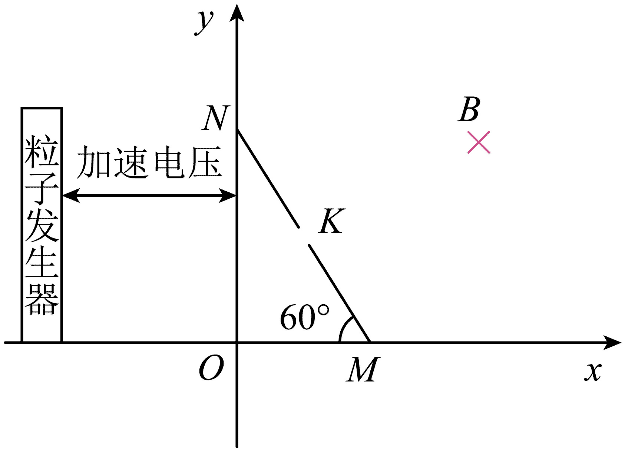．如图所示，在 Oxy 坐标系 x > 0，y > 0 区域内充满垂直纸面向里，磁感应强度大小为 B 的匀强磁场。磁场中放置一长度为 L 的挡板，其两端分别位于x、y轴上 M、N 两点，∠OMN = 60°，挡板上有一小孔 K 位于 MN 中点。△OMN 之外的第一象限区域存在恒定匀强电场。位于 y 轴左侧的粒子发生器在 0 < y < \(\frac{{\sqrt 3 }}{2}\)L 的范围内可以产生质量为 m，电荷量为 + q 的无初速度的粒子。粒子发生器与 y 轴之间存在水平向右的匀强加速电场，加速电压大小可调，粒子经此电场加速后进入磁场，挡板厚度不计，粒子可沿任意角度穿过小孔，碰撞挡板的粒子不予考虑，不计粒子重力及粒子间相互作用力。

（1）求使粒子垂直挡板射入小孔 K 的加速电压 U₀；

（2）调整加速电压，当粒子以最小的速度从小孔 K 射出后恰好做匀速直线运动，求第一象限中电场强度的大小和方向；

（3）当加速电压为 \(\frac{{q{B^2}{L^2}}}{{24m}}\) 时，求粒子从小孔 K 射出后，运动过程中距离 y 轴最近位置的坐标。

【答案】

（1）U₀ = \(\frac{{q{B^2}{L^2}}}{{8m}}\)

（2）E = \(\frac{{q{B^2}L}}{{4m}}\)，方向沿 x 轴正方向

（3）d_m = \(\frac{{(3 - \sqrt 3 )L}}{{12}}\)