1．极板间一蜡烛火焰带有正离子、电子以及其他的带电粒子，两极板电压保持不变，当电极板距离减小时，电场强度如何变？电子受力方向？（    ）

A．电场强度增大，方向向左             B．电场强度增大，方向向右

C．电场强度减小，方向向左              D．电场强度减小，方向向右

【答案】

B

【解析】

由题知，两极板电压保持不变，则根据电势差和电场强度的关系有 E = \(\frac{U}{d}\)，当电极板距离减小时，电场强度 E 增大，再结合题图可知极板间的电场线水平向左，则可知电子受到的电场力方向向右。

故选 B。

 

2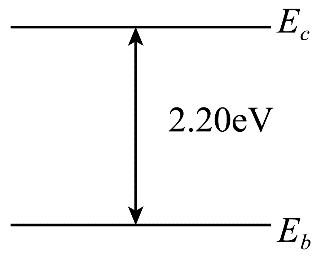．近年来，江西省科学家发明硅衬底氮化镓基系列发光二极管，开创了国际上第三条 LED 技术路线。某氮化镓基 LED 材料的简化能级如图所示，若能级差为 2.20 eV（约 3.52×10⁻¹⁹ J），普朗克常量 h = 6.63×10⁻³⁴ J·s，则发光频率约为（    ）

A．6.38×10¹⁴ Hz                    B．5.67×10¹⁴ Hz

C．5.31×10¹⁴ Hz                    D．4.67×10¹⁴ Hz

【答案】

C

 

3．某物体位置随时间的关系为 x = 1 + 2t + 3t²，则关于其速度与 1 s 内的位移大小，下列说法正确的是（    ）

A．速度是刻画物体位置变化快慢的物理量，1 s 内的位移大小为 6 m

B．速度是刻画物体位移变化快慢的物理量，1 s 内的位移大小为 6 m

C．速度是刻画物体位置变化快慢的物理量，1 s 内的位移大小为 5 m

D．速度是刻画物体位移变化快慢的物理量，1 s 内的位移大小为 5 m

【答案】

C

【解析】

根据速度的定义式 v = \(\frac{{\Delta x}}{{\Delta t}}\) 表明，速度等于位移与时间的比值。位移是物体在一段时间内从一个位置到另一个位置的位置变化量，而时间是这段时间的长度。这个定义强调了速度不仅描述了物体运动的快慢，还描述了物体运动的方向。因此，速度是刻画物体位置变化快慢的物理量。

再根据物体位置随时间的关系 x = 1 + 2t + 3t²，可知开始时物体的位置 x₀ = 1 m，1 s 时物体的位置 x₁ = 6 m，则 1 s 内物体的位移为 Δx = x₁ − x₀ = 5 m。

故选 C。

 

4．两个质量相同的卫星绕月球做匀速圆周运动，半径分别为 r₁、r₂，则动能和周期的比值为（    ）

A．\(\frac{{{E_{k1}}}}{{{E_{k2}}}}\) = \(\frac{{{r_2}}}{{{r_1}}}\)，\(\frac{{{T_1}}}{{{T_2}}}\) = \(\frac{{\sqrt {r_1^3} }}{{\sqrt {r_2^3} }}\)                  B．\(\frac{{{E_{k1}}}}{{{E_{k2}}}}\) = \(\frac{{{r_1}}}{{{r_2}}}\)，\(\frac{{{T_1}}}{{{T_2}}}\) = \(\frac{{\sqrt {r_1^3} }}{{\sqrt {r_2^3} }}\)

C．\(\frac{{{E_{k1}}}}{{{E_{k2}}}}\) = \(\frac{{{r_2}}}{{{r_1}}}\)，\(\frac{{{T_1}}}{{{T_2}}}\) =  \(\frac{{\sqrt {r_2^3} }}{{\sqrt {r_1^3} }}\)                  D．\(\frac{{{E_{k1}}}}{{{E_{k2}}}}\) = \(\frac{{{r_1}}}{{{r_2}}}\)，\(\frac{{{T_1}}}{{{T_2}}}\) =  \(\frac{{\sqrt {r_2^3} }}{{\sqrt {r_1^3} }}\)

【答案】

A

 

5．庐山瀑布“飞流直下三千尺，疑是银河落九天”瀑布高 150 m，水流量 10 m³/s，假设利用瀑布来发电，能量转化效率为 70%，则发电功率为（    ）

A．10⁹            B．10⁷            C．10⁵            D．10³

【答案】

B

 

6．如图（a）所示，利用超声波可以检测飞机机翼内部缺陷。在某次检测实验中，入射波为连续的正弦信号，探头先后探测到机翼表面和缺陷表面的反射信号，分别如图（b）、（c）所示。已知超声波在机翼材料中的波速为 6300 m/s。关于这两个反射信号在探头处的叠加效果和缺陷深度 d，下列选项正确的是（    ）

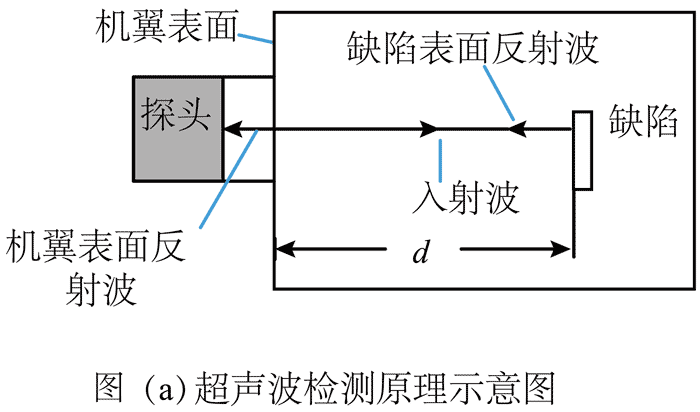
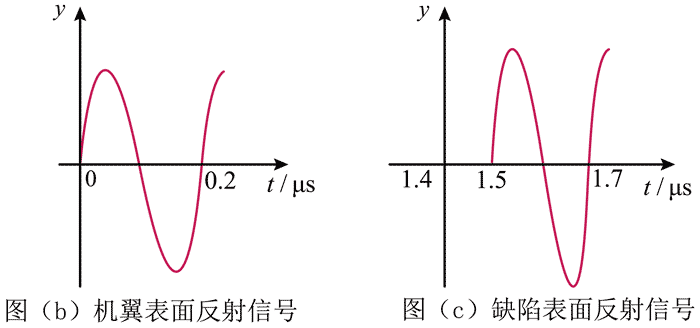
A．振动减弱；d = 4.725 mm               B．振动加强；d = 4.725 mm

C．振动减弱；d = 9.45 mm                 D．振动加强；d = 9.45 mm

【答案】

A

 

7．石墨烯是一种由碳原子组成的单层二维蜂窝状晶格结构新材料，具有丰富的电学性能．现设计一电路测量某二维石墨烯样品的载流子（电子）浓度。如图（a）所示，在长为 a，宽为 b 的石墨烯表面加一垂直向里的匀强磁场，磁感应强度为 B，电极 1、3 间通以恒定电流 I，电极 2、4 间将产生电压 U。当 I = 1.00×10⁻³ A 时，测得 U – B 关系图线如图（b）所示，元电荷 e = 1.60×10⁻¹⁹ C，则此样品每平方米载流子数最接近（    ）

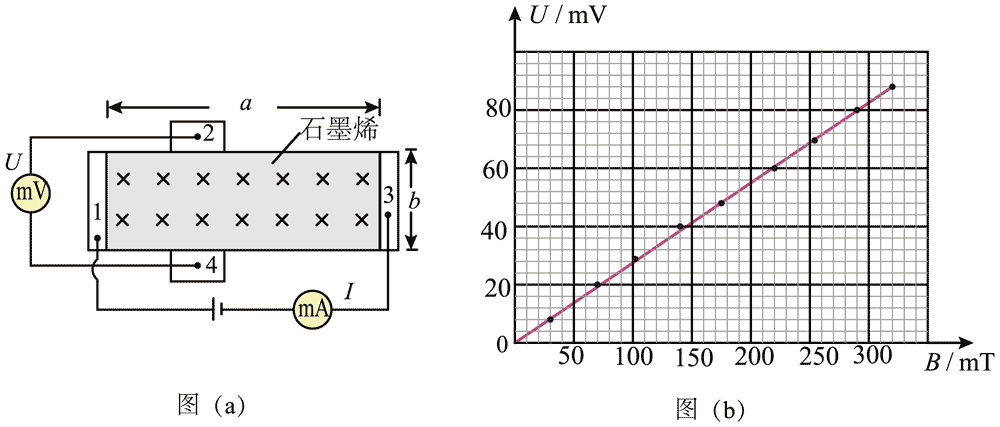
A．1.7×10¹⁹           B．1.7×10¹⁵           C．2.3×10²⁰           D．2.3×10¹⁶

【答案】

D

 

8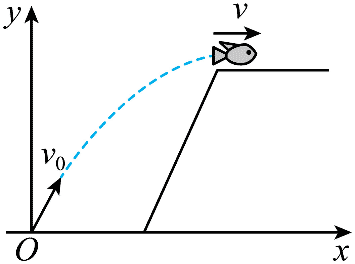．一条河流某处存在高度差，小鱼从低处向上跃出水面，冲到高处．如图所示，以小鱼跃出水面处为坐标原点，x 轴沿水平方向，建立坐标系，小鱼的初速度为 v₀，末速度 v 沿 x 轴正方向。在此过程中，小鱼可视为质点且只受重力作用。关于小鱼的水平位置 x、竖直位置 y、水平方向分速度 v_x 和竖直方向分速度 v_y 与时间 t 的关系，下列图像可能正确的是（    ）

【答案】

AD

 

9．某同学用普通光源进行双缝干涉测光的波长实验。下列说法正确的是（     ）

A．光具座上依次摆放光源、透镜、滤光片、双缝、单缝、遮光筒、测量头等元件

B．透镜的作用是使光更集中

C．单缝的作用是获得线光源

D．双缝间距越小，测量头中观察到的条纹数目内越多

【答案】

BC

 

10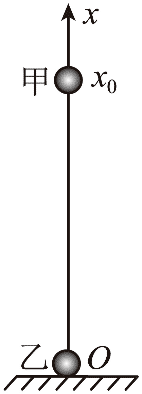．如图所示，垂直于水平桌面固定一根轻质绝缘细直杆，质量均为 m、带同种电荷的绝缘小球甲和乙穿过直杆，两小球均可视为点电荷，带电荷量分别为q和 Q。在图示的坐标系中，小球乙静止在坐标原点，初始时刻小球甲从 x = x₀ 处由静止释放，开始向下运动。甲和乙两点电荷的电势能 E_p = k \(\frac{{Qq}}{r}\)（r 为两点电荷之间的距离，k 为静电力常量）。最大静摩擦力等于滑动摩擦力 f，重力加速度为 g。关于小球甲，下列说法正确的是（     ）

A．最低点的位置 x = \(\frac{{kQq}}{{(mg + f){x_0}}}\)

B．速率达到最大值时的位置 x = \(\sqrt {\frac{{kQq}}{{mg - f}}} \)

C．最后停留位置 x 的区间是 \(\sqrt {\frac{{kQq}}{{mg}}} \) ≤ x ≤ \(\sqrt {\frac{{kQq}}{{mg - f}}} \)

D．若在最低点能返回，则初始电势能 E_p0 < (mg − f)\(\sqrt {\frac{{kQq}}{{mg + f}}} \)

【答案】

BD

 

11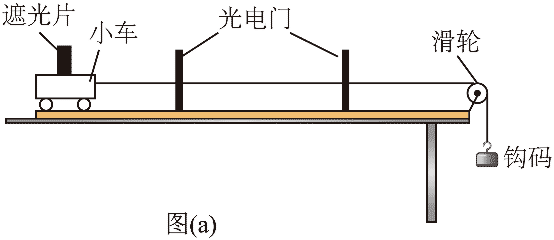．某小组探究物体加速度与其所受合外力的关系。实验装置如图（a）所示，水平轨道上安装两个光电门，小车上固定一遮光片，细线一端与小车连接，另一端跨过定滑轮挂上钩码。

（1）实验前调节轨道右端滑轮高度，使细线与轨道平行，再适当垫高轨道左端以平衡小车所受摩擦力。

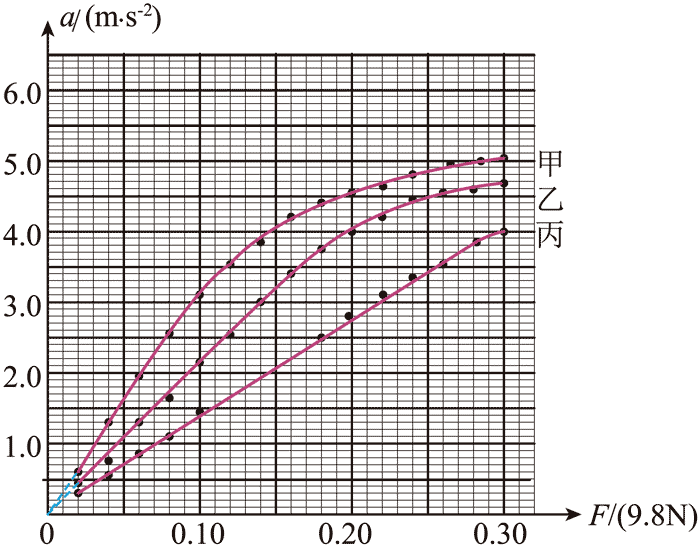
（2）小车的质量为 M₁ = 320 g。利用光电门系统测出不同钩码质量 m 时小车加速度 a。钩码所受重力记为 F，作出 a – F 图像，如图（b）中图线甲所示。

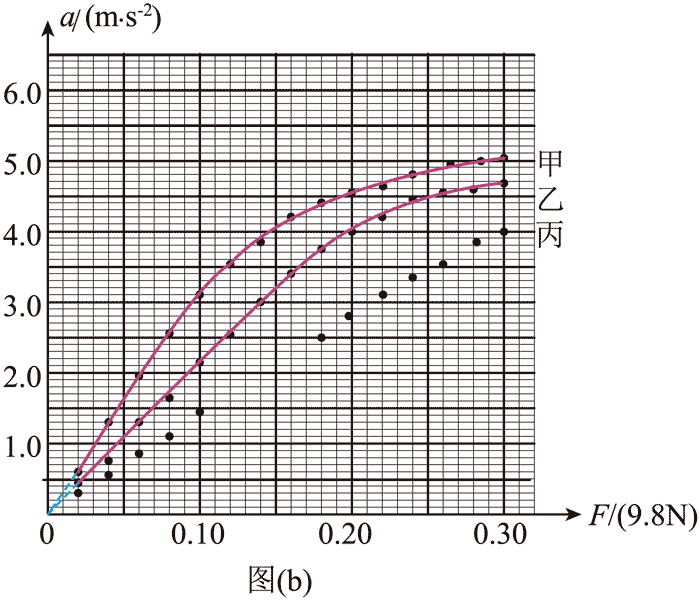
（3）由图线甲可知，F 较小时，a 与 F 成正比；F 较大时，a 与 F 不成正比。为了进一步探究，将小车的质量增加至 M₂ = 470 g，重复步骤（2）的测量过程，作出 a – F 图像，如图（b）中图线乙所示。

（4）与图线甲相比，图线乙的线性区间____________，非线性区间____________。再将小车的质量增加至 M₃ = 720 g，重复步骤（2）的测量过程，记录钩码所受重力 F 与小车加速度 a，如表所示（表中第 9 ~ 14 组数据未列出）。

序号	1	2	3	4	5
钩码所受重力 F/9.8 N	0.020	0.040	0.060	0.080	0.100
小车加速度 a/m·s−2	0.26	0.55	0.82	1.08	1.36
序号	6	7	8	9 ~ 14	15
钩码所受重力 F/9.8 N	0.120	0.140	0.160	…	0.300
小车加速度 a/m·s−2	1.67	1.95	2.20	…	3.92

（5）请在图（b）中补充描出第 6 至 8 三个数据点，并补充完成图线丙_________。

（6）根据以上实验结果猜想和推断：小车的质量____________时，a 与 F 成正比。结合所学知识对上述推断进行解释：______________________。

【答案】

（4）较大，较小

（5）

（6）远大于钩码质量。

设绳子拉力为 T，对钩码根据牛顿第二定律有 F – T = ma

对小车根据牛顿第二定律有 T = Ma

联立解得 F = (M + m)a

变形得 a = \(\frac{1}{{m + M}}\)F

当 m ≪ M 时，可认为 m + M = M

则 a = \(\frac{1}{M}\)F

即 a 与 F 成正比。

 

12．某小组欲设计一种电热水器防触电装置，其原理是：当电热管漏电时，利用自来水自身的电阻，可使漏电电流降至人体安全电流以下。为此，需先测量水的电阻率，再进行合理设计。

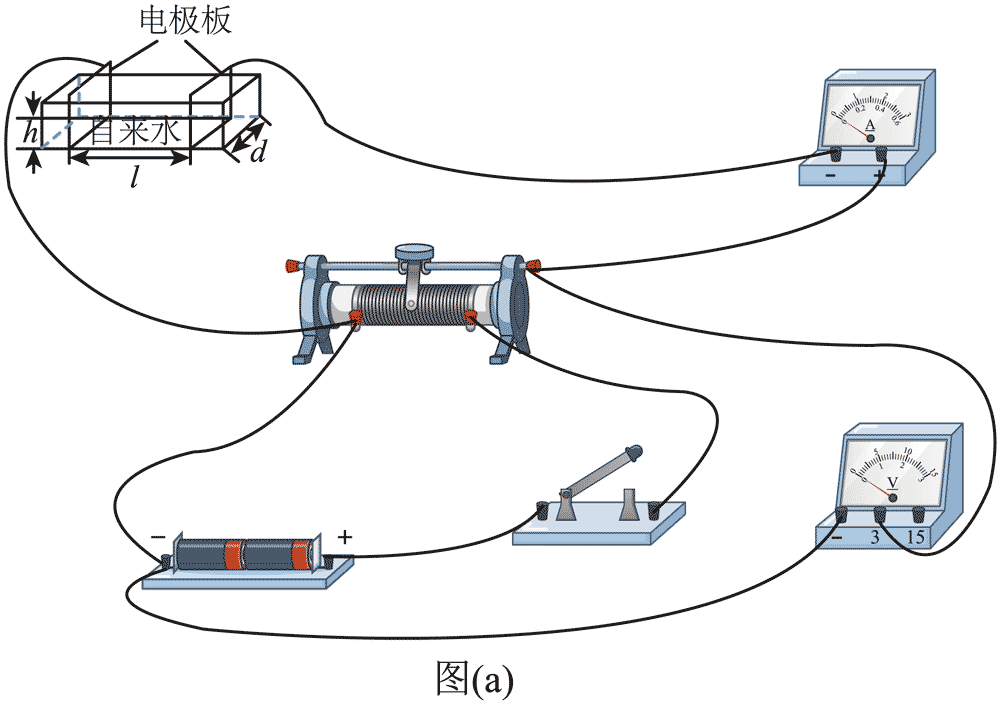
（1）如图（a）所示，在绝缘长方体容器左右两侧安装可移动的薄金属板电极，将自来水倒入其中，测得水的截面宽 d = 0.07 m 和高 h = 0.03 m。

（2）现有实验器材：电流表（量程 300 μA，内阻 R_A = 2500 Ω）、电压表（量程 3 V 或 15 V，内阻未知）、直流电源（3 V）、滑动变阻器、开关和导线．请在图（a）中画线完成电路实物连接_____。

（3）连接好电路，测量 26℃ 的水在不同长度 l 时的电阻值 R_x。将水温升到 65℃，重复测量。绘出 26℃ 和 65℃ 水的 R_x – l 图，分别如图（b）中甲、乙所示。

（4）若 R_x – l 图线的斜率为 k，则水的电阻率表达 ρ =____________（用 k、d、h 表示）。实验结果表明，温度____________（填“高”或“低”）的水更容易导电。

（5）测出电阻率后，拟将一段塑料水管安装于热水器出水口作为防触电装置。为保证出水量不变，选用内直径为 8.0×10⁻³ m 的水管。若人体的安全电流为 1.0×10⁻³ A，热水器出水温度最高为 65℃，忽略其他电阻的影响（相当于热水器 220 V 的工作电压直接加在水管两端），则该水管的长度至少应设计为____________m。（保留两位有效数字）

【答案】

（2）

（4）kdh，高

（5）0.46

 

13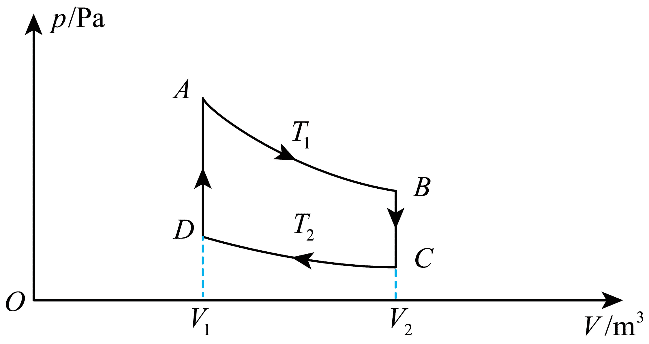．可逆斯特林热机的工作循环如图所示。一定质量的理想气体经 ABCDA 完成循环过程，AB 和 CD 均为等温过程，BC 和 DA 均为等容过程。已知 T₁ = 1200 K，T₂ = 300 K，气体在状态 A 的压强 p_A = 8.0×10⁵ Pa，体积 V₁ = 1.0 m³，气体在状态 C 的压强 p_C = 1.0×10⁵ Pa。求：

（1）气体在状态 D 的压强 p_D；

（2）气体在状态 B 的体积 V₂。

【答案】

（1）2×10⁵ Pa

（2）2.0 m³

 

14．雪地转椅是一种游乐项目，其中心传动装置带动转椅在雪地上滑动。如图（a）、（b）所示，传动装置有一高度可调的水平圆盘，可绕通过中心 O 点的竖直轴匀速转动。圆盘边缘 A 处固定连接一轻绳，轻绳另一端 B 连接转椅（视为质点）。转椅运动稳定后，其角速度与圆盘角速度相等。转椅与雪地之间的动摩擦因数为 μ，重力加速度为 g，不计空气阻力。

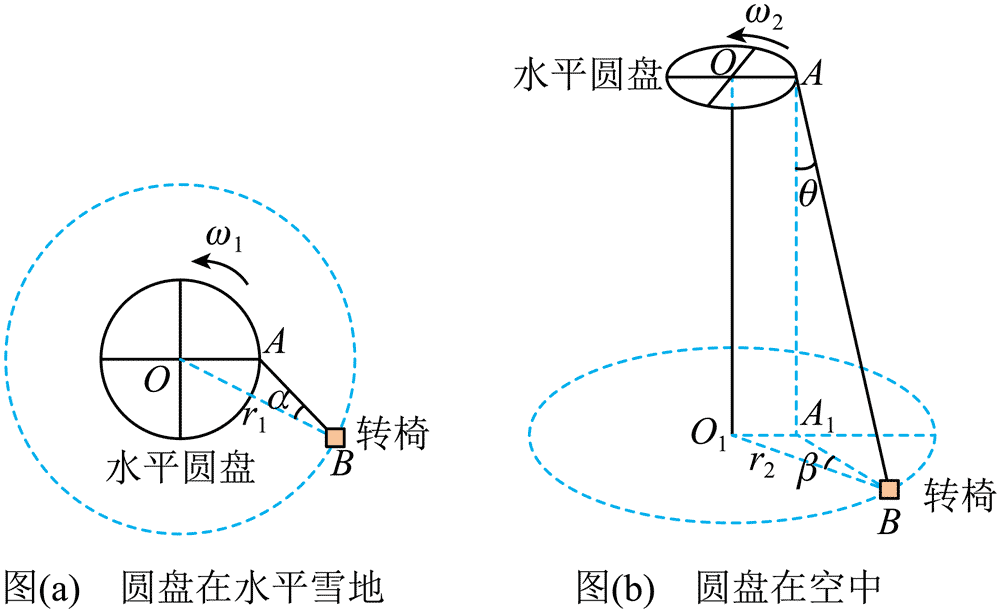
（1）在图（a）中，若圆盘在水平雪地上以角速度 ω₁ 匀速转动，转椅运动稳定后在水平雪地上绕 O 点做半径为 r₁ 的匀速圆周运动。求 AB 与 OB 之间夹角 α 的正切值。

（2）将圆盘升高，如图（b）所示。圆盘匀速转动，转椅运动稳定后在水平雪地上绕 O₁ 点做半径为 r₂ 的匀速圆周运动，绳子与竖直方向的夹角为 θ，绳子在水平雪地上的投影 A₁B 与 O₁B 的夹角为 β。求此时圆盘的角速度 ω₂。

【答案】

（1）\(\frac{{\mu g}}{{\omega _1^2{r_1}}}\)

（2）ω₂ = \(\sqrt {\frac{{\mu g\sin \theta \cos \beta }}{{(\sin \theta \sin \beta  + \mu \cos \theta ){r_2}}}} \)

 

15．如图（a）所示，轨道左侧斜面倾斜角满足 sinθ₁ = 0.6，摩擦因数 μ₁ = \(\frac{3}{20}\)，足够长的光滑水平导轨处于磁感应强度为 B = 0.5 T 的匀强磁场中，磁场方向竖直向上，右侧斜面导轨倾角满足 sinθ₂ = 0.8，摩擦因数 μ₂ = \(\frac{83}{144}\)。现将质量为 m_甲 = 6 kg 的导体杆甲从斜面上高 h = 4 m 处由静止释放，质量为 m_乙 = 2 kg 的导体杆乙静止在水平导轨上，与水平轨道左端的距离为 d。已知导轨间距为l = 2m，两杆电阻均为 R = 1 Ω，其余电阻不计，不计导体杆通过水平导轨与斜面导轨连接处的能量损失，且若两杆发生碰撞，则为完全非弹性碰撞，取 g = 10 m/s²，求：

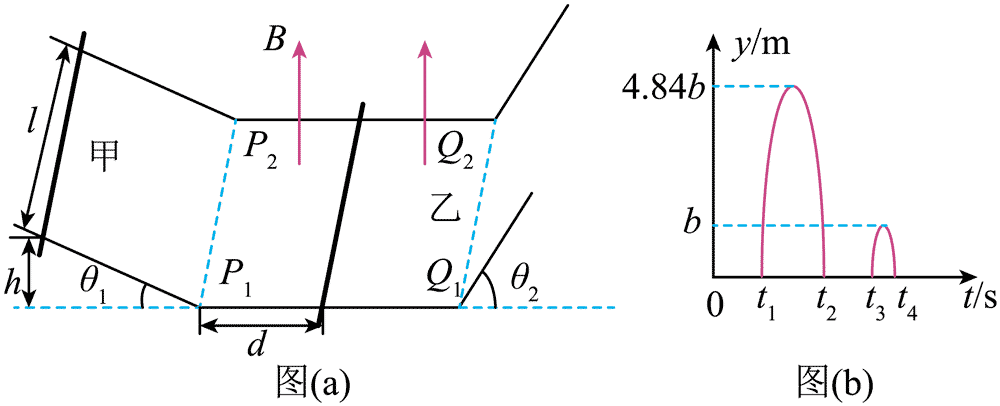
（1）甲杆刚进入磁场，乙杆的加速度？

（2）乙杆第一次滑上斜面前两杆未相碰，距离 d 满足的条件？

（3）若乙前两次在右侧倾斜导轨上相对于水平导轨的竖直高度 y 随时间 t 的变化如图（b）所示（t₁、t₂、t₃、t₄、b 均为未知量），乙第二次进入右侧倾斜导轨之前与甲发生碰撞，甲在 0 ~ t₃ 时间内未进入右侧倾斜导轨，求 d 的取值范围。

【答案】

（1）a_乙0 = 2 m/s²，方向水平向右

（2）d ≥ 24 m

（3）\(\frac{356}{11}\) m < d < \(\frac{696}{11}\) m