1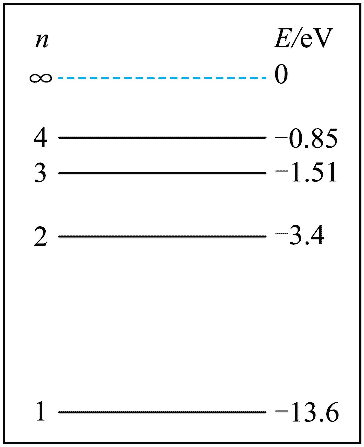．大连相干光源是我国第一台高增益自由电子激光用户装置，其激光辐射所应用的玻尔原子理论很好地解释了氢原子的光谱特征。图为氢原子的能级示意图，已知紫外光的光子能量大于 3.11 eV，当大量处于 n = 3 能级的氢原子向低能级跃迁时，辐射不同频率的紫外光有（    ）

A．1 种         B．2 种         C．3 种         D．4 种

【答案】

B

 

2．某同学参加户外拓展活动，遵照安全规范，坐在滑板上，从高为 h 的粗糙斜坡顶端由静止下滑，至底端时速度为 v。已知人与滑板的总质量为 m，可视为质点．重力加速度大小为 g，不计空气阻力．则此过程中人与滑板克服摩擦力做的功为（    ）

A．mgh           B．\(\frac{1}{2}\)mv²       C．mgh + \(\frac{1}{2}\)mv²           D．mgh − \(\frac{1}{2}\)mv²

【答案】

D

【解析】

人在下滑的过程中，由动能定理可得

mgh − W_f = \(\frac{1}{2}\)mv² − 0

可得此过程中人与滑板克服摩擦力做的功为 W_f = mgh − \(\frac{1}{2}\)mv²

故选 D。

 

3．某仪器发射甲、乙两列横波，在同一均匀介质中相向传播，波速 v 大小相等。某时刻的波形图如图所示，则这两列横波（    ）

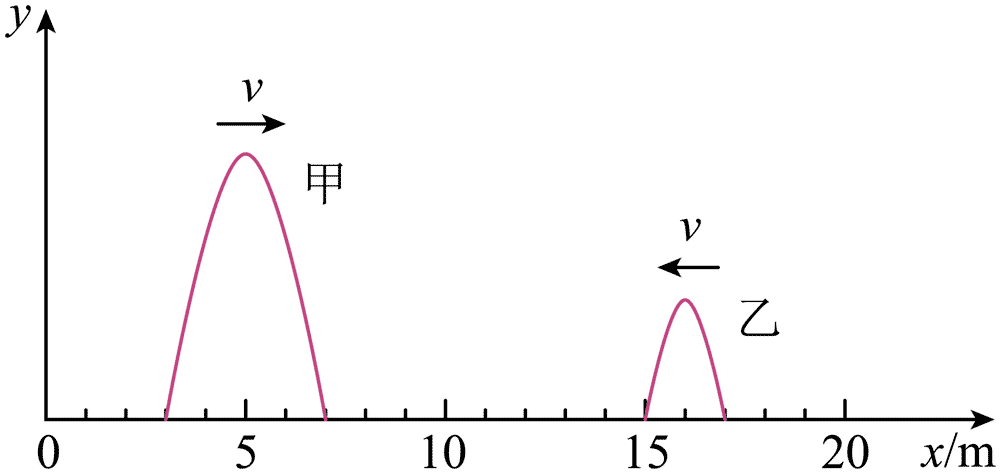
A．在 x = 9.0 m 处开始相遇              B．在 x = 10 m 处开始相遇

C．波峰在 x = 10.5 m  处相遇            D．波峰在 x = 11.5 m 处相遇

【答案】

C

【解析】

AB．由题意可知两列波的波速相同，所以相同时间内传播的的距离相同，故两列横波在 x = 11.0 m 处开始相遇，故 AB 错误；

CD．甲波峰的坐标为 x₁ = 5 m，乙波峰的坐标为 x₂ = 16 m，由于两列波的波速相同，所以波峰在 xʹ = 5 m + \(\frac{{16 - 5}}{2}\) =10.5 m 处相遇，故 C 正确，D 错误。

故选 C。

 

4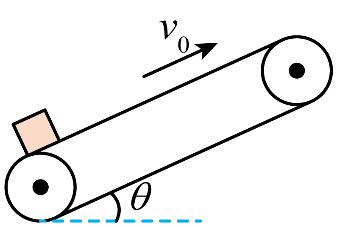．倾角为 θ 的传送带以恒定速率 v₀ 顺时针转动。t = 0 时在传送带底端无初速轻放一小物块，如图所示。t₀ 时刻物块运动到传送带中间某位置，速度达到 v₀。不计空气阻力，则物块从传送带底端运动到顶端的过程中，加速度 a、速度 v 随时间 t 变化的关系图线可能正确的是（    ）

【答案】

C

【解析】

0 ~ t₀ 时间内：物体轻放在传送带上，做加速运动。受力分析可知，物体受重力、支持力、滑动摩擦力，滑动摩擦力大于重力的下滑分力，合力不变，故做匀加速运动。

t₀ 之后：当物块速度与传送带相同时，静摩擦力与重力的下滑分力相等，加速度突变为零，物块做匀速直线运动。

C 正确，ABD 错误。

故选 C。

 

5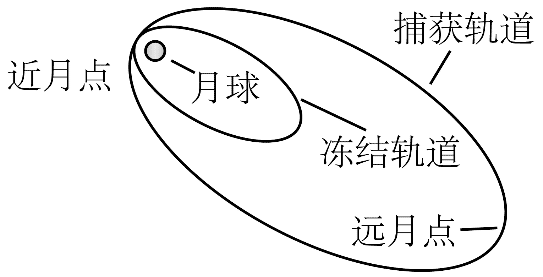．2024 年 3 月 20 日，我国探月工程四期鹊桥二号中继星成功发射升空。当抵达距离月球表面某高度时，鹊桥二号开始进行近月制动，并顺利进入捕获轨道运行，如图所示，轨道的半长轴约为 51 900 km。后经多次轨道调整，进入冻结轨道运行，轨道的半长轴约为 9 900 km，周期约为 24 h。则鹊桥二号在捕获轨道运行时（    ）

A．周期约为 144 h

B．近月点的速度大于远月点的速度

C．近月点的速度小于在冻结轨道运行时近月点的速度

D．近月点的加速度大于在冻结轨道运行时近月点的加速度

【答案】

B

【解析】

A．冻结轨道和捕获轨道的中心天体是月球，根据开普勒第三定律 \(\frac{{T_1^2}}{{R_1^3}}\) = \(\frac{{T_2^2}}{{R_2^3}}\)

整理得 T₂ = \(\sqrt {\frac{{R_2^3}}{{R_1^3}}} \)T₁ = 288 h

A 错误；

B．根据开普勒第二定律得，近月点的速度大于远月点的速度，B 正确；

C．近月点从捕获轨道到冻结轨道鹊桥二号进行近月制动，捕获轨道近月点的速度大于在冻结轨道运行时近月点的速度，C 错误；

D．两轨道的近月点所受的万有引力相同，根据牛顿第二定律可知，近月点的加速度等于在冻结轨道运行时近月点的加速度，D 错误。

故选 B。

 

6．如图所示，竖直平面内有两完全相同的轻质弹簧，它们的一端分别固定于水平线上的 M、N 两点，另一端均连接在质量为 m 的小球上。开始时，在竖直向上的拉力作用下，小球静止于 MN 连线的中点 O，弹簧处于原长。后将小球竖直向上。缓慢拉至 P 点，并保持静止，此时拉力 F 大小为  2mg。已知重力加速度大小为 g，弹簧始终处于弹性限度内，不计空气阻力。若撤去拉力，则小球从 P 点运动到 O 点的过程中（    ）

A．速度一直增大                          B．速度先增大后减小

C．加速度的最大值为 3g           D．加速度先增大后减小

【答案】

A

【解析】

AB．缓慢拉至 P 点，保持静止，由平衡条件可知此时拉力 F 与重力和两弹簧的拉力合力为零。此时两弹簧的合力为大小为 mg。当撤去拉力，则小球从 P 点运动到 O 点的过程中两弹簧的拉力与重力的合力始终向下，小球一直做加速运动，故 A 正确，B 错误；

CD．小球从 P 点运动到 O 点的过程中，形变量变小弹簧在竖直方向的合力不断变小，故小球受的合外力一直变小，加速度的最大值为撤去拉力时的加速度，由牛顿第二定律可知

2mg = ma

加速度的最大值为 2g，CD 错误。

故选 A。

 

7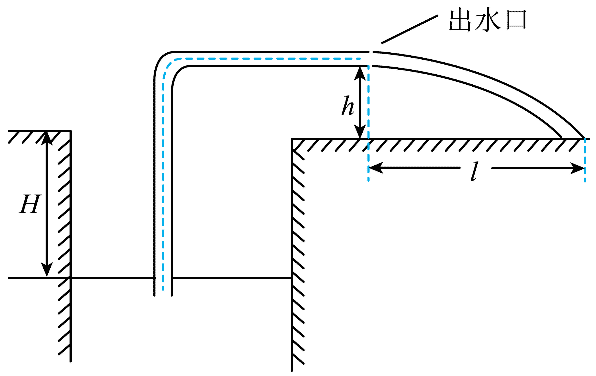．在某地区的干旱季节，人们常用水泵从深水井中抽水灌溉农田，简化模型如图所示。水井中的水面距离水平地面的高度为 H。出水口距水平地面的高度为 h，与落地点的水平距离约为 l。假设抽水过程中 H 保持不变，水泵输出能量的 η 倍转化为水被抽到出水口处增加的机械能。已知水的密度为 ρ，水管内径的横截面积为 S，重力加速度大小为 g，不计空气阻力。则水泵的输出功率约为（    ）

A．\(\frac{{\rho gSl\sqrt {2gh} }}{{2\eta h}}\left( {H + h + \frac{{{l^2}}}{{2h}}} \right)\)          B．\(\frac{{\rho gSl\sqrt {2gh} }}{{2\eta h}}\left( {H + h + \frac{{{l^2}}}{{4h}}} \right)\)

C．\(\frac{{\rho gSl\sqrt {2gh} }}{{2\eta h}}\left( {H + \frac{{{l^2}}}{{2h}}} \right)\)                  D．\(\frac{{\rho gSl\sqrt {2gh} }}{{2\eta h}}\left( {H + \frac{{{l^2}}}{{4h}}} \right)\)

【答案】

B

 

8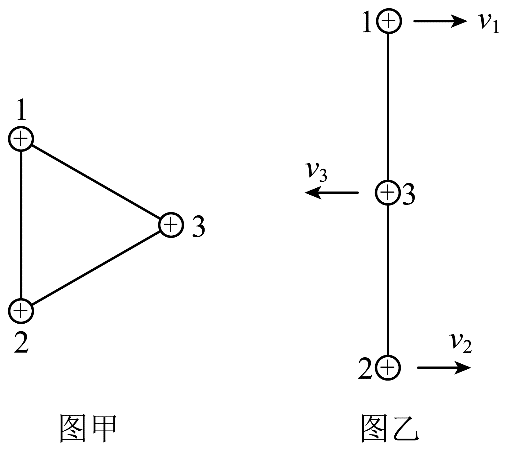．在某装置中的光滑绝缘水平面上，三个完全相同的带电小球，通过不可伸长的绝缘轻质细线，连接成边长为 d 的正三角形，如图甲所示。小球质量为 m，带电量为 + q，可视为点电荷。初始时，小球均静止，细线拉直。现将球 1 和球 2 间的细线剪断，当三个小球运动到同一条直线上时，速度大小分别为 v₁、v₂、v₃，如图乙所示。该过程中三个小球组成的系统电势能减少了 \(\frac{{k{q^2}}}{{2d}}\)，k 为静电力常量，不计空气阻力。则（    ）

A．该过程中小球 3 受到的合力大小始终不变         B．该过程中系统能量守恒，动量不守恒

C．在图乙位置，v₁ = v₂，v₃ ≠ 2v₁                           D．在图乙位置，v₃ = \(\sqrt {\frac{{2k{q^2}}}{{3md}}} \)

【答案】

D

 

9．一倾角为 30° 足够大的光滑斜面固定于水平地面上，在斜面上建立 Oxy 直角坐标系，如图（1）所示。从 t = 0 开始，将一可视为质点的物块从 O 点由静止释放，同时对物块施加沿 x 轴正方向的力 F₁ 和 F₂，其大小与时间 t 的关系如图（2）所示。己知物块的质量为 1.2 kg，重力加速度 g 取 10 m/s²，不计空气阻力。则（    ）

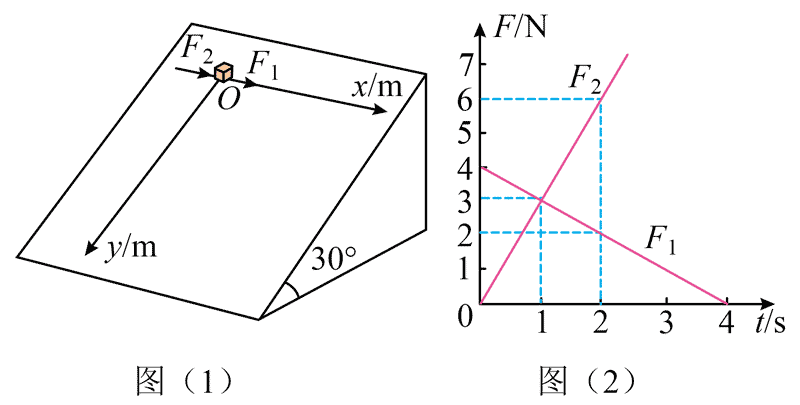
A．物块始终做匀变速曲线运动

B．t = 1 s 时，物块的 y 坐标值为 2.5 m

C．t = 1 s 时，物块的加速度大小为 5\(\sqrt 3 \) m/s²

D．t = 2 s 时，物块的速度大小为 10\(\sqrt 2 \) m/s

【答案】

 BD

 

10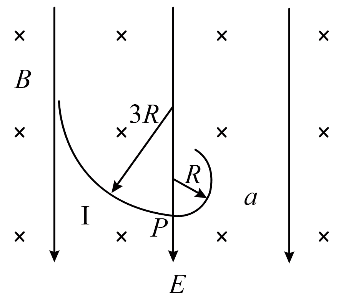．空间中存在竖直向下的匀强电场和垂直于纸面向里的匀强磁场，电场强度大小为 E，磁感应强度大小为 B。一质量为 m 的带电油滴 a，在纸面内做半径为 R 的圆周运动，轨迹如图所示。当 a 运动到最低点 P 时，瞬间分成两个小油滴 Ⅰ、Ⅱ，二者带电量、质量均相同。Ⅰ 在 P 点时与 a 的速度方向相同，并做半径为 3R 的圆周运动，轨迹如图所示。Ⅱ 的轨迹未画出。己知重力加速度大小为 g，不计空气浮力与阻力以及 Ⅰ、Ⅱ 分开后的相互作用，则（    ）

A．油滴 a 带负电，所带电量的大小为 \(\frac{{mg}}{E}\)

B．油滴 a 做圆周运动的速度大小为 \(\frac{{gBR}}{E}\)

C．小油滴 Ⅰ 做圆周运动的速度大小为 ，周期为 \(\frac{{3gBR}}{E}\)

D．小油滴 Ⅱ 沿顺时针方向做圆周运动 \(\frac{{4\pi E}}{{gB}}\)

【答案】

ABD

 

11．某实验小组做“测量玻璃的折射率”及拓展探究实验。

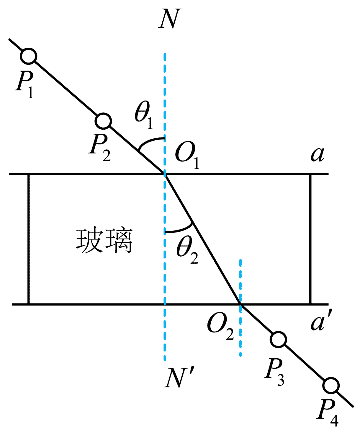（1）为测量玻璃的折射率，按如图所示进行实验，以下表述正确的一项是________。（填正确答案标号）

A．用笔在白纸上沿着玻璃砖上边和下边分别画出直线 a 和 aʹ

B．在玻璃砖一侧插上大头针 P₁、P₂，眼睛在另一侧透过玻璃砖看两个大头针，使 P₂ 把 P₁ 挡住，这样就可以确定入射光线和入射点 O₁。在眼睛这一侧，插上大头针 P₃，使它把 P₁、P₂ 都挡住，再插上大头针 P₄，使它把 P₁、P₂、P₃ 都挡住，这样就可以确定出射光线和出射点 O₂

C．实验时入射角 θ₁ 应尽量小一些，以减小实验误差

（2）为探究介质折射率与光的频率的关系，分别用一束红光和一束绿光从同一点入射到空气与玻璃的分界面．保持相同的入射角，根据实验结果作出光路图，并标记红光和绿光，如图乙所示．此实验初步表明：对于同一种介质，折射率与光的频率有关。频率大，折射率________（填“大”或“小”）

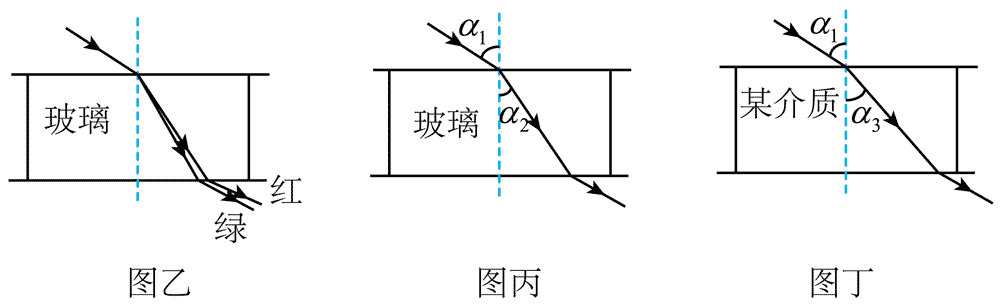
（3）为探究折射率与介质材料的关系，用同一束微光分别入射玻璃砖和某透明介质，如图丙、丁所示。保持相同的入射角 α₁，测得折射角分别为 α₂、α₃（α₂ < α₃），则玻璃和该介质的折射率大小关系为 n_玻璃________n_介质（填“>”或“<”）。此实验初步表明：对于一定频率的光，折射率与介质材料有关。

【答案】

（1）B

（2）大

（3）>

 

12．某实验小组要将电流表 G（铭牌标示：I_g = 500 μA，R_g = 800 Ω）改装成量程为 1 V 和 3 V 的电压表，并用标准电压表对其进行校准。选用合适的电源、滑动变阻器、电阻箱、开关和标准电压表等实验器材，按图（1）所示连接电路，其中虚线框内为改装电路。

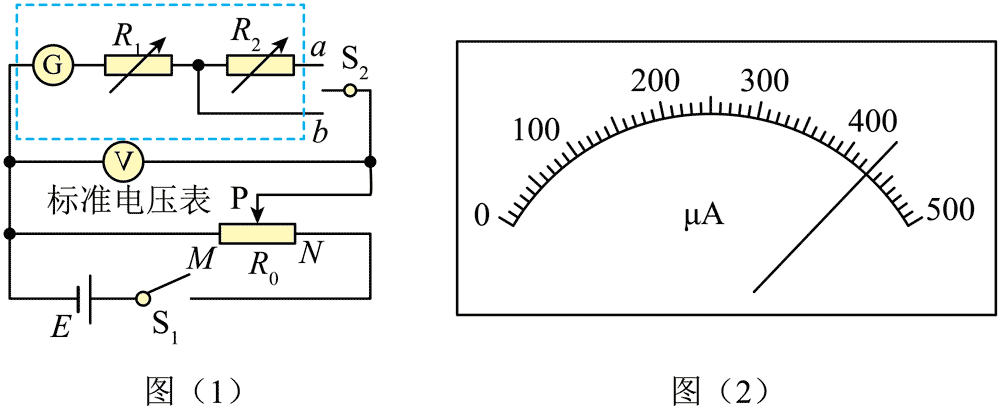
（1）开关 S₁ 闭合前，滑片 P 应移动到________（填“M”或“N”）端。

（2）根据要求和已知信息，电阻箱 R₁ 的阻值已调至 1200 Ω，则 R₂ 的阻值应调至________Ω。

（3）当单刀双掷开关 S₂ 与 a 连接时，电流表 G 和标准电压表 V 的示数分别为 I、U，则电流表 G 的内阻可表示为________。（结果用U、I、R₁、R₂ 表示）

（4）校准电表时，发现改装后电压表的读数始终比标准电压表的读数偏大，经排查发现电流表 G 内阻的真实值与铭牌标示值有偏差，则只要________即可。（填正确答案标号）

A．增大电阻箱 R₁ 的阻值

B．减小电阻箱 R₂ 的阻值

C．将滑动变阻器的滑片 P 向 M 端滑动

（5）校准完成后，开关 S₂ 与 b 连接，电流表 G 的示数如图（2）所示，此示数对应的改装电压表读数为________V。（保留 2 位有效数字）

【答案】

（1）M

（2）4000

（3）R_g =  \(\frac{U}{I}\) − R₁ – R₂

（4）A

（5）0.86

【解析】

（1）由图可知，该滑动变阻器采用分压式接法，为了电路，在开关 S₁ 闭合前，滑片 P 应移到 M 端；

（2）当开关 S₂ 接 b 时，电压表量程为 1 V，根据欧姆定律

U₁ = I_g（R_g + R₁）

当开关 S₂ 接 a 时，电压表量程为 3 V，根据欧姆定律

U₂ = I_g（R_g + R₁ + R₂）

其中 R₁ = 1200 Ω

联立解得 R₂ = 4000 Ω

（3）当开关 S₂ 接 a 时，根据欧姆定律 U = I(R_g + R₁ + R₂)

可得电流表 G 的内阻可表示为 R_g = \(\frac{U}{I}\) − R₁ – R₂

（4）校准电表时，发现改装后电压表的读数始终比标准电压表的读数偏大，可知电流表 G 内阻的真实值小于铭牌标示值，根据闭合电路的欧姆定律可以增大两电阻箱的阻值。

故选 A。

（5）根据闭合电路欧姆定律 U_V = I_A（R_g + R₁）= 430×10⁻⁶×(800 + 1200) V = 0.86 V

 

13．某人驾驶汽车，从北京到哈尔滨，在哈尔滨发现汽车的某个轮胎内气体的压强有所下降（假设轮胎内气体的体积不变，且没有漏气，可视为理想气体）。于是在哈尔滨给该轮胎充入压强与大气压相同的空气，使其内部气体的压强恢复到出发时的压强（假设充气过程中，轮胎内气体的温度与环境相同，且保持不变）。已知该轮胎内气体的体积 V₀ = 30 L，从北京出发时，该轮胎气体的温度 t₁ = − 3 ℃，压强 p₁ = 2.7×10⁵ Pa。哈尔滨的环境温度 t₂ = − 23 ℃，大气压强 p₀ 取 1.0×10⁵ Pa。求：

（1）在哈尔滨时，充气前该轮胎气体压强的大小。

（2）充进该轮胎的空气体积。

【答案】

（1）2.5×10⁵ Pa

（2）6 L

 

14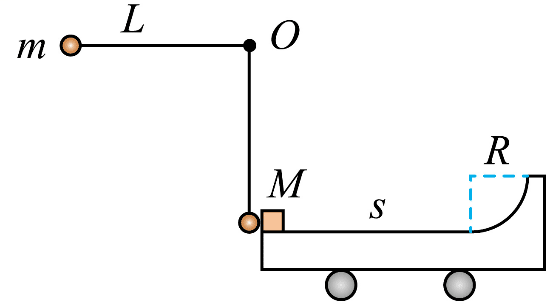．如图所示，一实验小车静止在光滑水平面上，其上表面有粗糙水平轨道与光滑四分之一圆弧轨道。圆弧轨道与水平轨道相切于圆弧轨道最低点，一物块静止于小车最左端，一小球用不可伸长的轻质细线悬挂于 O 点正下方，并轻靠在物块右侧。现将细线拉直到水平位置时，静止释放小球，小球运动到最低点时与物块发生弹性碰撞。碰撞后，物块沿着的轨道运动，已知细线长 L = 1.25 m。小球质量 m = 0.20 kg。物块、小车质量均为 M = 0.30 kg。小车上的水平轨道长 s = 1.0 m。圆弧轨道半径 R = 0.15 m。小球、物块均可视为质点。不计空气阻力，重力加速度 g 取 10 m/s²。

（1）求小球运动到最低点与物块碰撞前所受拉力的大小；

（2）求小球与物块碰撞后的瞬间，物块速度的大小；

（3）为使物块能进入圆弧轨道，且在上升阶段不脱离小车，求物块与水平轨道间的动摩擦因数 μ 的取值范围。

【答案】

（1）6 N

（2）4 m/s

（3）0.25 ≤ μ < 0.4

 

15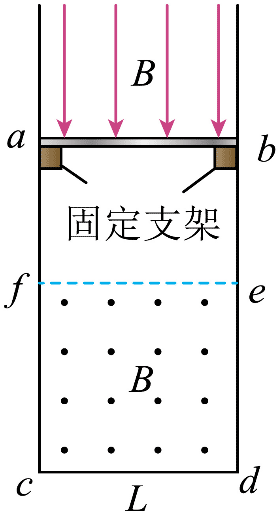．如图所示，一“U”型金属导轨固定在竖直平面内，一电阻不计，质量为m的金属棒 ab 垂直于导轨，并静置于绝缘固定支架上。边长为 L 的正方形 cdef 区域内，存在垂直于纸面向外的匀强磁场。支架上方的导轨间，存在竖直向下的匀强磁场。两磁场的磁感应强度大小 B 随时间的变化关系均为 B = kt（SI），k 为常数（k > 0）。支架上方的导轨足够长，两边导轨单位长度的电阻均为 r，下方导轨的总电阻为 R。t = 0 时，对 ab 施加竖直向上的拉力，恰使其向上做加速度大小为 a 的匀加速直线运动，整个运动过程中 ab 与两边导轨接触良好。已知 ab 与导轨间动摩擦因数为 μ，重力加速度大小为 g。不计空气阻力，两磁场互不影响。

（1）求通过面积 S_cdef 的磁通量大小随时间 t 变化的关系式，以及感应电动势的大小，并写出 ab 中电流的方向；

（2）求 ab 所受安培力的大小随时间 t 变化的关系式；

（3）求经过多长时间，对 ab 所施加的拉力达到最大值，并求此最大值。

【答案】

（1）kL²t，kL²，从 a 流向 b

（2）F_安 = \(\frac{{{k^2}{L^3}t}}{{R + ar{t^2}}}\)

（3）\(\frac{{\mu {k^2}{L^3}}}{{2\sqrt {Rar} }}\) + m(g + a)