1．量子技术是当前物理学应用研究的热点，下列关于量子论的说法正确的是（    ）

A．普朗克认为黑体辐射的能量是连续的

B．光电效应实验中，红光照射可以让电子从某金属表面逸出，若改用紫光照射也可以让电子从该金属表面逸出

C．康普顿研究石墨对 X 射线散射时，发现散射后仅有波长小于原波长的射线成分

D．德布罗意认为质子具有波动性，而电子不具有波动性

【答案】

B

【解析】

A．普朗克认为黑体辐射的能量是一份一份的，是量子化的，故 A 错误；

B．产生光电效应的条件是光的频率大于金属的极限频率，紫光的频率大于红光，若红光能使金属发生光电效应，可知紫光也能使该金属发生光电效应，故 B 正确；

C．石墨对 X 射线的散射过程遵循动量守恒，光子和电子碰撞后，电子获得一定的动量，光子动量变小，根据 λ = \(\frac{h}{p}\) 可知波长变长，故 C 错误；

D．德布罗意认为物质都具有波动性，包括质子和电子，故 D 错误。

故选 B。

 

2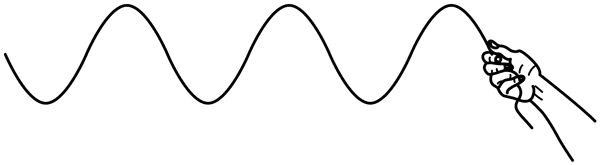．如图，健身者在公园以每分钟 60 次的频率上下抖动长绳的一端，长绳自右向左呈现波浪状起伏，可近似为单向传播的简谐横波。长绳上 A、B 两点平衡位置相距 6 m，t₀ 时刻 A 点位于波谷，B 点位于波峰，两者之间还有一个波谷。下列说法正确的是（    ）

A．波长为 3 m                                               B．波速为 12 m/s

C．t₀ + 0.25 s 时刻，B 点速度为 0            D．t₀ + 0.50 s 时刻，A 点速度为 0

【答案】

D

【解析】

A．如图根据题意可知 x_AB = 1.5λ = 6 m，解得 λ = 4 m。故 A 错误；

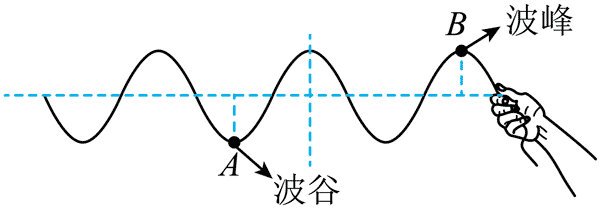
B．波源的振动频率为 f = 1 Hz，故波速为 v= λf = 4 m/s。故 B 错误；

C．质点的振动周期为 T= 1 s，因为 0.25 s = T/4，故 B 点在 t₀ + 0.25 s 运动到平衡位置，位移为 0，速度最大，故 C 错误；

D．0.5 s = T/2，故 A 点在 t₀ + 0.50 s 运动到波峰，位移最大，速度为 0，故 D 正确。

故选 D。

 

3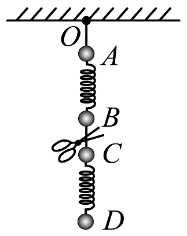．如图，质量分别为 4m、3m、2m、m 的四个小球 A、B、C、D，通过细线或轻弹簧互相连接，悬挂于 O 点，处于静止状态，重力加速度为 g。若将 B、C 间的细线剪断，则剪断瞬间 B 和 C 的加速度大小分别为（    ）

A．g，1.5g            B．2g，1.5g          C．2g，0.5g          D．g，0.5g

【答案】

A

 

4．如图，有一硬质导线 Oabc，其中 abc  是半径为 R 的半圆弧，b 为圆弧的中点，直线段 Oa 长为 R 且垂直于直径 ac。该导线在纸面内绕 O 点逆时针转动，导线始终在垂直纸面向里的匀强磁场中。则 O、a、b、c 各点电势关系为（    ）

A．φ_O > φ_a > φ_b > φ_c      B．φ_O < φ_a < φ_b < φ_c

C．φ_O > φ_a > φ_b = φ_c      D．φ_O < φ_a < φ_b = φ_c

【答案】

C

【解析】

 

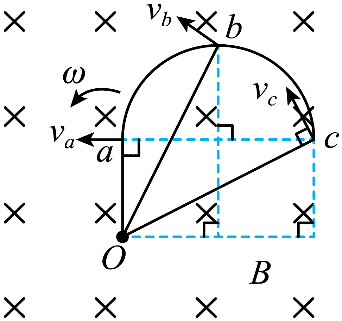
5．真空中有电荷量为 + 4q 和 – q 的两个点电荷，分别固定在 x 轴上 – 1 和 0 处。设无限远处电势为 0，x 正半轴上各点电势 φ 随 x 变化的图像正确的是（    ）

【答案】

D

 

6．根据国家能源局统计，截止到 2023 年 9 月，我国风电装机 4 亿千瓦，连续 13 年居世界第一位，湖南在国内风电设备制造领域居于领先地位。某实验小组模拟风力发电厂输电网络供电的装置如图所示。已知发电机转子以角速度 ω 匀速转动，升、降压变压器均为理想变压器，输电线路上的总电阻可简化为一个定值电阻 R₀。当用户端接一个定值电阻 R 时，R₀ 上消耗的功率为 P。不计其余电阻，下列说法正确的是（    ）

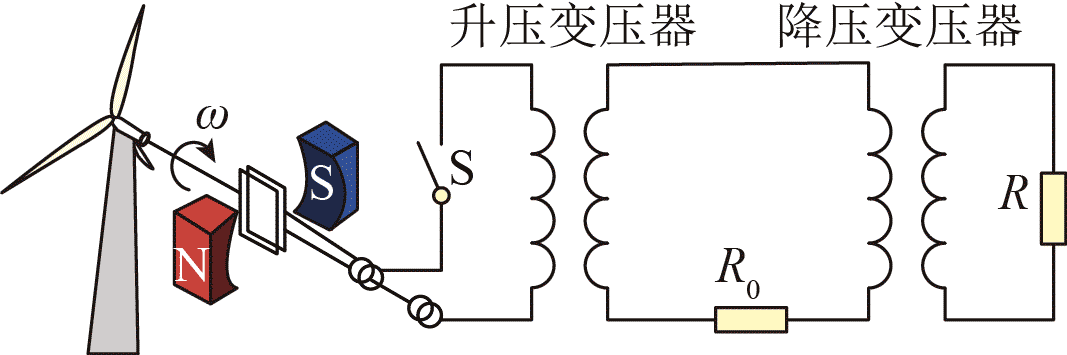
A．风速增加，若转子角速度增加一倍，则 R₀ 上消耗的功率为 4P

B．输电线路距离增加，若 R₀ 阻值增加一倍，则 R₀ 消耗的功率为 4P

C．若升压变压器的副线圈匝数增加一倍，则 R₀ 上消耗的功率为 8P

D．若在用户端再并联一个完全相同的电阻 R，则 R₀ 上消耗的功率为 6P

【答案】

A

 

7．2024 年 5 月 3 日，“嫦娥六号”探测器顺利进入地月转移轨道，正式开启月球之旅。相较于“嫦娥四号”和“嫦娥五号”，本次的主要任务是登陆月球背面进行月壤采集并通过升空器将月壤转移至绕月运行的返回舱，返回舱再通过返回轨道返回地球。设返回舱绕月运行的轨道为圆轨道，半径近似为月球半径。己知月球表面重力加速度约为地球表面的 \(\frac{1}{6}\)，月球半径约为地球半径的 \(\frac{1}{4}\)。关于返回舱在该绕月轨道上的运动，下列说法正确的是（    ）

A．其相对于月球的速度大于地球第一宇宙速度

B．其相对于月球的速度小于地球第一宇宙速度

C．其绕月飞行周期约为地球上近地圆轨道卫星周期的 \(\sqrt {\frac{2}{3}} \) 倍

D．其绕月飞行周期约为地球上近地圆轨道卫星周期的 \(\sqrt {\frac{3}{2}} \) 倍

【答案】

BD

 

8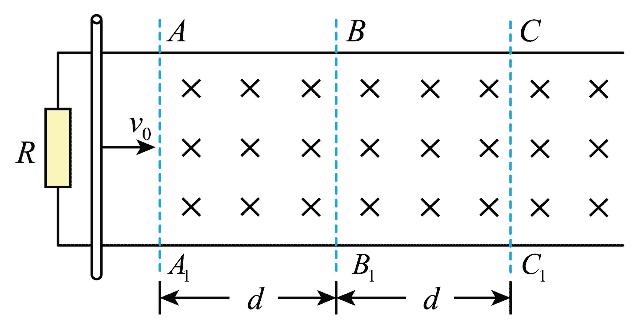．某电磁缓冲装置如图所示，两足够长的平行金属导轨置于同一水平面内，导轨左端与一阻值为 R 的定值电阻相连，导轨 BC 段与 B₁C₁ 段粗糙，其余部分光滑，AA₁ 右侧处于竖直向下的匀强磁场中，一质量为 m 的金属杆垂直导轨放置。现让金属杆以初速度 v₀ 沿导轨向右经过 AA₁ 进入磁场，最终恰好停在 CC₁ 处。已知金属杆接入导轨之间的阻值为 R，与粗糙导轨间的摩擦因数为 μ，AB = BC = d。导轨电阻不计，重力加速度为 g，下列说法正确的是（    ）

A．金属杆经过 BB₁ 的速度为 \({\frac{v_0}{2}}\)

B．在整个过程中，定值电阻 R 产生的热量为 \({\frac{1}{2}}\)mv₀² − \({\frac{1}{2}}\)μmgd

C．金属杆经过 AA₁B₁B 与 BB₁C₁C 区域，金属杆所受安培力的冲量相同

D．若将金属杆的初速度加倍，则金属杆在磁场中运动的距离大于原来的 2 倍

【答案】

CD

 

9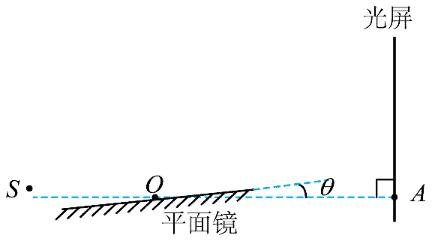．1834 年，洛埃利用平面镜得到杨氏双缝干涉的结果（称洛埃镜实验），平面镜沿 OA 放置，靠近并垂直于光屏。某同学重复此实验时，平面镜意外倾斜了某微小角度 θ，如图所示。S 为单色点光源。下列说法正确的是（    ）

A．沿 AO 向左略微平移平面镜，干涉条纹不移动

B．沿 OA 向右略微平移平面镜，干涉条纹间距减小

C．若 θ = 0°，沿 OA 向右略微平移平面镜，干涉条纹间距不变

D．若 θ = 0°，沿 AO 向左略微平移平面镜，干涉条纹向 A 处移动

【答案】

BC

【解析】

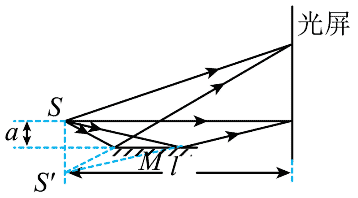CD．根据题意画出光路图。

如图所示，S 发出的光与通过平面镜反射光（可以等效成虚像 S′ 发出的光）是同一列光分成的，满足相干光条件。所以实验中的相干光源之一是通过平面镜反射的光，且该干涉可看成双缝干涉，设 S 与 S′ 的距离为 d，则 d = 2a，S 到光屏的距离为 l，代入双缝干涉公式 Δx = \({\frac{l}{d}}\) λ 可得 Δx = \({\frac{l}{2a}}\) λ。

则若 θ = 0°，沿 OA 向右（沿 AO 向左）略微平移平面镜，对 l 和 d 均没有影响，则干涉条纹间距不变，也不会移动，故 C 正确，D 错误；

AB．同理再次画出光路图。

沿 OA 向右略微平移平面镜，即图中从①位置→②位置，由图可看出双缝的间距增大，则干涉条纹间距减小，沿 AO 向左略微平移平面镜，即图中从②位置→①位置，由图可看出干涉条纹向上移动，故 A 错误，B 正确。

故选 BC。

 

10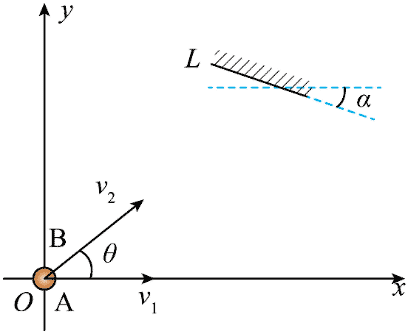．如图，光滑水平面内建立直角坐标系 xOy。A、B 两小球同时从 O 点出发，A 球速度大小为 v₁，方向沿x轴正方向，B 球速度大小为 v₂ = 2 m/s、方向与 x 轴正方向夹角为 θ。坐标系第一象限中有一个挡板 L，与 x 轴夹角为 α。B 球与挡板 L 发生碰撞，碰后 B 球速度大小变为 1 m/s，碰撞前后 B 球的速度方向与挡板 L 法线的夹角相同，且分别位于法线两侧。不计碰撞时间和空气阻力，若 A、B 两小球能相遇，下列说法正确的是（    ）

A．若 θ = 15°，则 v₁ 的最大值为 \(\sqrt 2 \) m/s，且 α = 15°

B．若 θ = 15°，则 v₁ 的最大值为 \(\frac{{2\sqrt 3 }}{3}\) m/s，且 α = 0°

C．若 θ = 30°，则 v₁ 的最大值为 \(\frac{{2\sqrt 3 }}{3}\) m/s，且 α = 0°

D．若 θ = 30°，则 v₁ 的最大值为 \(\sqrt 2 \) m/s，且 α = 15°

【答案】

AC

【解析】

 

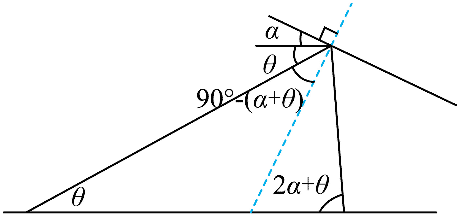
11．某实验小组要探究一金属丝的阻值随气压变化的规律，搭建了如图（a）所示的装置。电阻测量原理如图（b）所示，E 是电源，V 为电压表，A 为电流表。

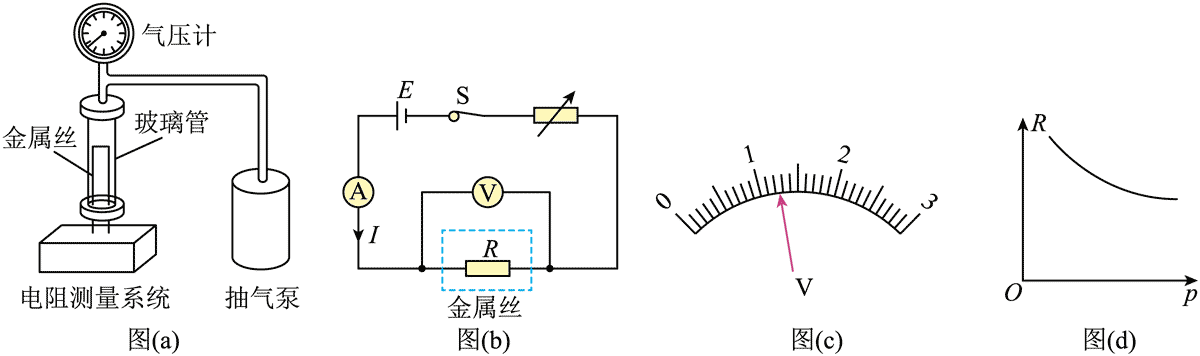
（1）保持玻璃管内压强为 1 个标准大气压，电流表示数为 100 mA，电压表量程为 3 V，表盘如图（c）所示，示数为________V，此时金属丝阻值的测量值 R 为________Ω（保留 3 位有效数字）；

（2）打开抽气泵，降低玻璃管内气压 p，保持电流 I 不变，读出电压表示数 U，计算出对应的金属丝阻值；

（3）根据测量数据绘制 R – p 关系图线，如图（d）所示；

（4）如果玻璃管内气压是 0.5 个标准大气压，保持电流为 100 mA，电压表指针应该在图（c）指针位置的________侧（填“左”或“右”）；

（5）若电压表是非理想电压表，则金属丝电阻的测量值________真实值（填“大于”“小于”或“等于”）。

【答案】

（1）1.23，12.3

（4）右侧

（5）小于

 

12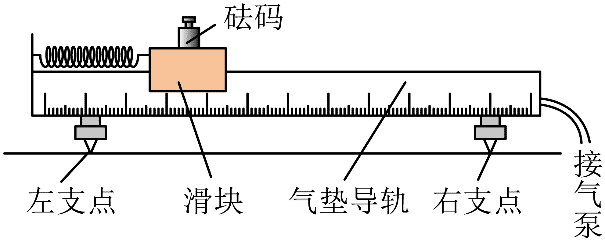．在太空，物体完全失重，用天平无法测量质量。如图，某同学设计了一个动力学方法测量物体质量的实验方案，主要实验仪器包括：气垫导轨、滑块、轻弹簧、标准砝码、光电计时器和待测物体，主要步骤如下：

（1）调平气垫导轨，将弹簧左端连接气垫导轨左端，右端连接滑块；

（2）将滑块拉至离平衡位置 20 cm 处由静止释放，滑块第 1 次经过平衡位置处开始计时，第 21 次经过平衡位置时停止计时，由此测得弹簧振子的振动周期 T；

（3）将质量为 m 的砝码固定在滑块上，重复步骤（2）；

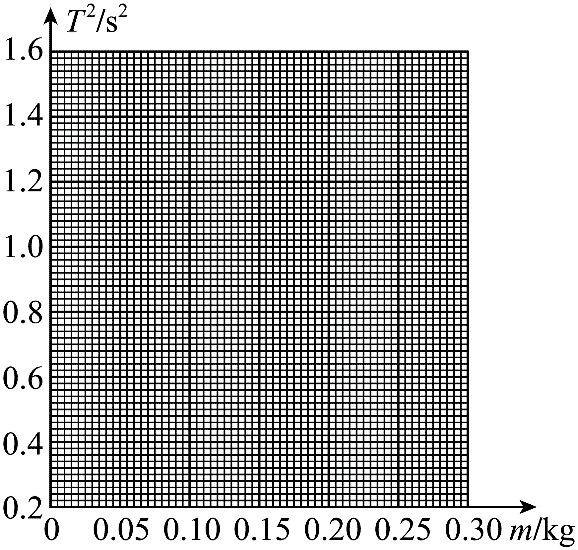（4）依次增加砝码质量 m，测出对应的周期 T，实验数据如下表所示，在图中绘制 T² – m 关系图线______；

m/kg	T/s	T2/s2
0.000	0.632	0.399
0.050	0.775	0.601
0.100	0.893	0.797
0.150	1.001	1.002
0.200	1.105	1.221
0.250	1.175	1381

（5）由 T² – m 图像可知，弹簧振子振动周期的平方与砝码质量的关系是________（填“线性的”或“非线性的”）；

（6）取下砝码后，将待测物体固定在滑块上，测量周期并得到 T² = 0.880s²，则待测物体质量是________kg（保留 3 位有效数字）；

（7）若换一个质量较小的滑块重做上述实验，所得 T² – m 图线与原图线相比将沿纵轴________移动（填“正方向”“负方向”或“不”）。

【答案】

（4）

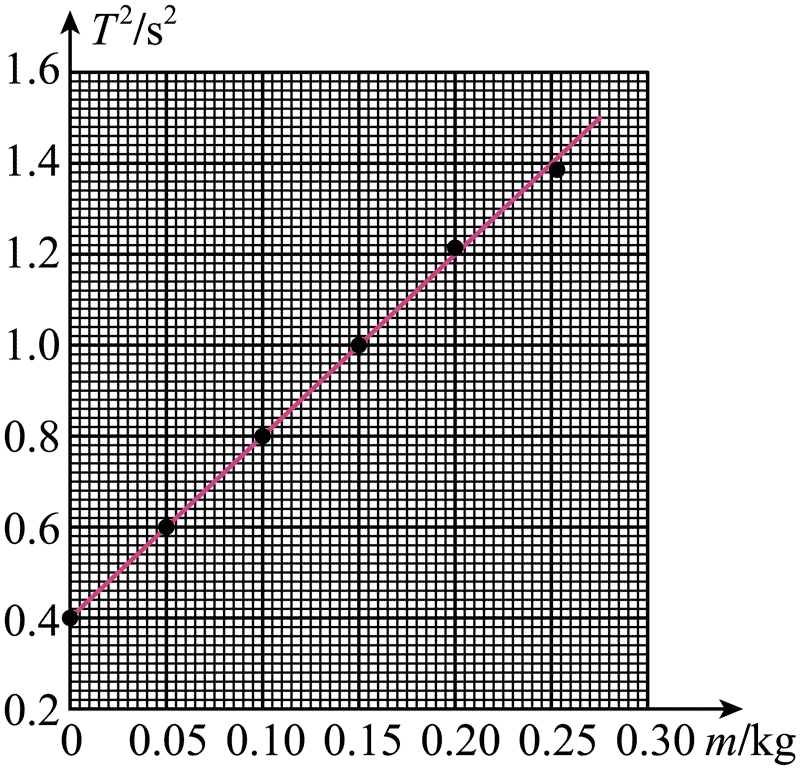
（5）线性的

（6）0.120

（7）负方向

 

13．一个充有空气的薄壁气球，气球内气体压强为 p、体积为 V。气球内空气可视为理想气体。

（1）若将气球内气体等温膨胀至大气压强 p₀，求此时气体的体积 V₀（用 p₀、p 和 V 表示）；

（2）小赞同学想测量该气球内气体体积V的大小，但身边仅有一个电子天平。将气球置于电子天平上，示数为 m = 8.66×10⁻³ kg（此时须考虑空气浮力对该示数的影响）。小赞同学查阅资料发现，此时气球内气体压强 p 和体积 V 还满足：(p − p₀)(V − V_B0) = C，其中 p₀ = 1.0×10⁵ Pa为大气压强，V_B0 = 0.5×10⁻³ m³ 为气球无张力时的最大容积，C = 18 J 为常数。已知该气球自身质量为 m₀ = 8.40×10⁻³ kg，外界空气密度为 ρ₀ = 1.3 kg/m³，求气球内气体体积 V 的大小。

【答案】

（1）\(\frac{{pV}}{{{p_0}}}\)

（2）5×10⁻³ m³

【解析】

（1）理想气体做等温变化，根据玻意耳定律有 pV = p₀V₀

解得 V₀ = \(\frac{{pV}}{{{p_0}}}\)

（2）设气球内气体质量为 m_气，则

m_气 = ρ₀V₀

对气球进行受力分析如图所示。根据气球的受力分析有

mg + ρ₀gV = m_气g + m₀g

结合题中 p 和 V 满足的关系为

(p − p₀)(V − V_B0) = C

解得 V = 5×10⁻³ m³

 

14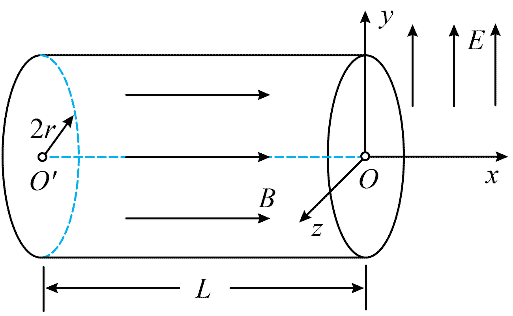．如图，有一内半径为 2r、长为 L 的圆筒，左右端面圆心 O′、O 处各开有一小孔。以 O 为坐标原点，取 O′O 方向为 x 轴正方向建立 xyz 坐标系。在筒内 x ≤ 0 区域有一匀强磁场，磁感应强度大小为 B，方向沿 x 轴正方向；筒外 x ≥ 0 区域有一匀强电场，场强大小为 E，方向沿y轴正方向。一电子枪在 O′ 处向圆筒内多个方向发射电子，电子初速度方向均在 xOy 平面内，且在 x 轴正方向的分速度大小均为 v₀。已知电子的质量为 m、电量为 e，设电子始终未与筒壁碰撞，不计电子之间的相互作用及电子的重力。

（1）若所有电子均能经过 O 进入电场，求磁感应强度 B 的最小值；

（2）取（1）问中最小的磁感应强度 B，若进入磁场中电子的速度方向与 x 轴正方向最大夹角为 θ，求 tanθ 的绝对值；

（3）取（1）问中最小的磁感应强度 B，求电子在电场中运动时 y 轴正方向的最大位移。

【答案】

（1）\(\frac{{2\pi m{v_0}}}{{eL}}\)

（2）\(\frac{{2\pi r}}{L}\)

（3）\(\frac{{2{\pi ^2}{r^2}v_0^2m}}{{Ee{L^2}}}\)

 

15．如图，半径为 R 的圆环水平放置并固定，圆环内有质量为 m_A 和 m_B 的小球 A 和 B（m_A > m_B）。初始时小球 A 以初速度 v₀ 沿圆环切线方向运动，与静止的小球 B 发生碰撞。不计小球与圆环之间的摩擦，两小球始终在圆环内运动。

（1）若小球 A 与 B 碰撞后结合在一起，求碰撞后小球组合体的速度大小及做圆周运动所需向心力的大小；

（2）若小球 A 与 B 之间为弹性碰撞，且所有的碰撞位置刚好位于等边三角形的三个顶点，求小球的质量比 \(\frac{{{m_{\rm{A}}}}}{{{m_{\rm{B}}}}}\)。

（3）若小球 A 与 B 之间为非弹性碰撞，每次碰撞后的相对速度大小为碰撞前的相对速度大小的 e 倍（0 < e < 1），求第 1 次碰撞到第 2n + 1 次碰撞之间小球 B 通过的路程。

【答案】

（1）v = \(\frac{{{m_{\rm{A}}}}}{{{m_{\rm{A}}} + {m_{\rm{B}}}}}\) v₀，F = \(\frac{{m_{\rm{A}}^{\rm{2}}v_0^2}}{{({m_{\rm{A}}} + {m_{\rm{B}}})R}}\)

（2）2 或 5

（3）\(\frac{{2\pi R{m_{\rm{A}}}}}{{{m_{\rm{A}}} + {m_{\rm{B}}}}} \cdot \frac{{{e^{2n}} - 1}}{{{e^n}(e - 1)}}\)