1．《梦溪笔谈》中记录了一次罕见的雷击事件：房屋被雷击后，屋内的银饰、宝刀等金属熔化了，但是漆器、刀鞘等非金属却完好（原文为：有一木格，其中杂贮诸器，其漆器银扣者，银悉熔流在地，漆器曾不焦灼。有一宝刀，极坚钢，就刀室中熔为汁，而室亦俨然）。导致金属熔化而非金属完好的原因可能为（    ）

A．摩擦         B．声波         C．涡流         D．光照

【答案】

C

【解析】

在雷击事件中金属和非金属都经历了摩擦，声波和光照的影响，而金属能够因电磁感应产生涡流非金属不能，因此可能原因为涡流。

故选 C。

 

2．硼中子俘获疗法是目前治疗癌症最先进的手段之一，¹⁰₅B + ¹₀n→^a₃X + ⁴_bY 是该疗法中一种核反应的方程，其中 X、Y 代表两种不同的原子核，则（    ）

A．a = 7，b = 1             B．a = 7，b = 2             C．a = 6，b = 1             D．a = 6，b = 2

【答案】

B

【解析】

由质量数和电荷数守恒可得 10 + 1 = a + 4，5 + 0 = 3 + b

解得 a = 7，b = 2

故选 B。

 

3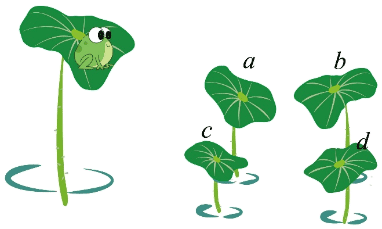．如图所示，有五片荷叶伸出荷塘水面，一只青蛙要从高处荷叶跳到低处荷叶上。设低处荷叶 a、b、c、d 和青蛙在同一竖直平面内，a、b 高度相同，c、d 高度相同，a、b 分别在 c、d 正上方。将青蛙的跳跃视为平抛运动，若以最小的初速度完成跳跃，则它应跳到（    ）

A．荷叶 a              B．荷叶 b              C．荷叶 c              D．荷叶 d

【答案】

C

【解析】

青蛙做平抛运动，水平方向匀速直线，竖直方向自由落体则有

x = vt，h = \(\frac{1}{2}\)gt²

可得 v = x\(\sqrt {\frac{g}{{2h}}} \)

因此水平位移越小，竖直高度越大初速度越小，因此跳到荷叶 c 上面。

故选 C。

 

4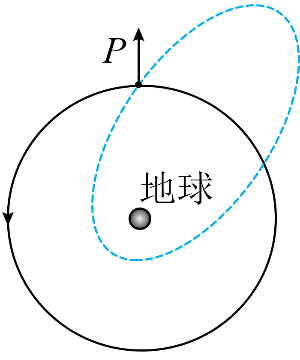．太空碎片会对航天器带来危害。设空间站在地球附近沿逆时针方向做匀速圆周运动，如图中实线所示。为了避开碎片，空间站在 P 点向图中箭头所指径向方向极短时间喷射气体，使空间站获得一定的反冲速度，从而实现变轨。变轨后的轨道如图中虚线所示，其半长轴大于原轨道半径。则（    ）

A．空间站变轨前、后在 P 点的加速度相同

B．空间站变轨后的运动周期比变轨前的小

C．空间站变轨后在 P 点的速度比变轨前的小

D．空间站变轨前的速度比变轨后在近地点的大

【答案】

A

【解析】

A．在 P 点变轨前后空间站所受到的万有引力不变，根据牛顿第二定律可知空间站变轨前、后在 P 点的加速度相同，故 A 正确；

B．因为变轨后其半长轴大于原轨道半径，根据开普勒第三定律可知空间站变轨后的运动周期比变轨前的大，故 B 错误；

C．变轨后在P点因反冲运动相当于瞬间获得竖直向下的速度，原水平向左的圆周运动速度不变，因此合速度变大，故 C 错误；

D．由于空间站变轨后在 P 点的速度比变轨前大，而比在近地点的速度小，则空间站变轨前的速度比变轨后在近地点的小，故 D 错误。

故选 A。

 

5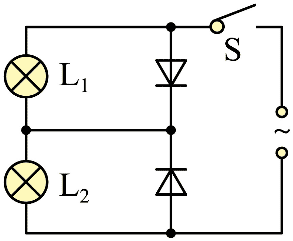．在如图所示电路中接入正弦交流电，灯泡 L₁ 的电阻是灯泡 L₂ 的 2 倍。假设两个二极管正向电阻为 0、反向电阻无穷大。闭合开关 S，灯泡 L₁、L₂ 的电功率之比 P₁∶P₂ 为（     ）

A．2︰1         B．1︰1         C．1︰2         D．1︰4

【答案】

C

【解析】

两个二极管正向电阻为 0，反向电阻无穷大，二极管导通则短路并联的灯泡，此时另一个灯泡与电源串联，根据电路图可知在一个完整的周期内，两个灯泡有电流通过的时间相等都为半个周期，电压有效值相等，则根据 P = \(\frac{{{U^2}}}{R}\) 可知 P₁∶P₂ = R_L2∶R_L1 = 1∶2。

故选 C。

 

6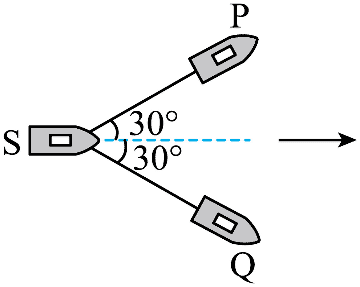．如图所示，两拖船 P、Q 拉着无动力货船 S 一起在静水中沿图中虚线方向匀速前进，两根水平缆绳与虚线的夹角均保持为 30°。假设水对三艘船在水平方向的作用力大小均为 f，方向与船的运动方向相反，则每艘拖船发动机提供的动力大小为（    ）

A．\(\frac{{\sqrt 3 }}{3}\)f         B．\(\frac{{\sqrt 21 }}{3}\)f                C．2f              D．3f

【答案】

B

 

7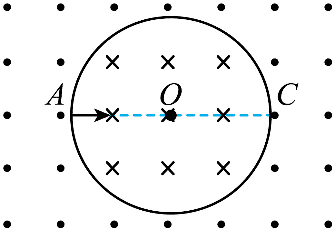．如图所示，在以 O 点为圆心、半径为 R 的圆形区域内有垂直于纸面向里的匀强磁场，磁感应强度大小为 B。圆形区域外有大小相等、方向相反、范围足够大的匀强磁场。一质量为 m、电荷量为 q（q > 0）的带电粒子沿直径 AC 方向从 A 点射入圆形区域。不计重力，下列说法正确的是（    ）

A．粒子的运动轨迹可能经过 O 点

B．粒子射出圆形区域时的速度方向不一定沿该区域的半径方向

C．粒子连续两次由 A 点沿 AC 方向射入圆形区域的最小时间间隔为 \(\frac{{7\pi m}}{{3qB}}\)

D．若粒子从 A 点射入到从 C 点射出圆形区域用时最短，粒子运动的速度大小为 \(\frac{{\sqrt 3 qBR}}{{3m}}\)

【答案】

D

 

8．关于电荷和静电场，下列说法正确的是（    ）

A．一个与外界没有电荷交换的系统，电荷的代数和保持不变

B．电场线与等势面垂直，且由电势低的等势面指向电势高的等势面

C．点电荷仅在电场力作用下从静止释放，该点电荷的电势能将减小

D．点电荷仅在电场力作用下从静止释放，将从高电势的地方向低电势的地方运动

【答案】

AC

【解析】

A．根据电荷守恒定律可知一个与外界没有电荷交换的系统，这个系统的电荷总量是不变的，故 A 正确；

B．根据电场线和等势面的关系可知电场线与等势面垂直，且由电势高的等势面指向电势低的等势面，故 B 错误；

CD．点电荷仅在电场力作用下从静止释放，电场力做正功，电势能减小，根据 φ = \(\frac{{{E_p}}}{q}\) 可知正电荷将从电势高的地方向电势低的地方运动，负电荷将从电势低的地方向电势高的地方运动，故 C 正确，D 错误。

故选 AC。

 

9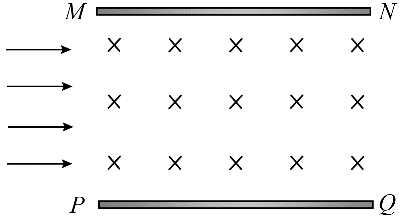．磁流体发电机的原理如图所示，MN 和 PQ 是两平行金属极板，匀强磁场垂直于纸面向里。等离子体（即高温下电离的气体，含有大量正、负带电粒子）从左侧以某一速度平行于极板喷入磁场，极板间便产生电压。下列说法正确的是（    ）

A．极板 MN 是发电机的正极

B．仅增大两极板间的距离，极板间的电压减小

C．仅增大等离子体的喷入速率，极板间的电压增大

D．仅增大喷入等离子体的正、负带电粒子数密度，极板间的电压增大

【答案】

AC

 

10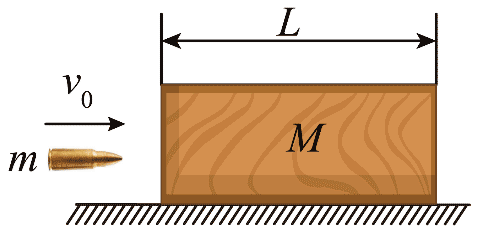．如图所示，在光滑水平面上静止放置一质量为 M、长为 L 的木块，质量为 m 的子弹水平射入木块。设子弹在木块内运动过程中受到的阻力不变，其大小 f 与射入初速度大小 v₀ 成正比，即 f = kv₀（k 为已知常数）。改变子弹的初速度大小 v₀，若木块获得的速度最大，则（    ）

A．子弹的初速度大小为 \(\frac{{2kL(m + M)}}{{mM}}\)

B．子弹在木块中运动的时间为 \(\frac{{2mM}}{{k(m + M)}}\)

C．木块和子弹损失的总动能为 \(\frac{{{k^2}{L^2}(m + M)}}{{mM}}\)

D．木块在加速过程中运动的距离为 \(\frac{{mL}}{{m + M}}\)

【答案】

AD

 

11．某同学利用激光测量半圆柱体玻璃砖的折射率，具体步骤如下：

①平铺白纸，用铅笔画两条互相垂直的直线 AAʹ 和 BBʹ，交点为 O。将半圆柱体玻璃砖的平直边紧贴 AAʹ，并使其圆心位于 O 点，画出玻璃砖的半圆弧轮廓线，如图（a）所示。

②将一细激光束沿 CO 方向以某一入射角射入玻璃砖，记录折射光线与半圆弧的交点 M。

③拿走玻璃砖，标记 CO 光线与半圆弧的交点 P。

④分别过 M、P 作 BBʹ 的垂线 MMʹ、PPʹ，Mʹ、Pʹ 是垂足，并用米尺分别测量 MMʹ、PPʹ 的长度 x 和 y。

⑤改变入射角，重复步骤②③④，得到多组 x 和 y 的数据。根据这些数据作出 y – x 图像，如图（b）所示。

（1）关于该实验，下列说法正确的是_____（单选，填标号）。

A．入射角越小，误差越小

B．激光的平行度好，比用插针法测量更有利于减小误差

C．选择圆心 O 点作为入射点，是因为此处的折射现象最明显

（2）根据 y – x 图像，可得玻璃砖的折射率为_____（保留三位有效数字）。

（3）若描画的半圆弧轮廓线半径略大于玻璃砖的实际半径，则折射率的测量结果_____（填“偏大”“偏小”或“不变”）。

【答案】

（1）B

（2）1.57

（3）不变

 

12．某同学设计了一个测量重力加速度大小 g 的实验方案，所用器材有：2 g 砝码若干、托盘 1 个、轻质弹簧 1 根、米尺 1 把、光电门 1 个、数字计时器 1 台等。

具体步骤如下：

①将弹簧竖直悬挂在固定支架上，弹簧下面挂上装有遮光片的托盘，在托盘内放入一个砝码，如图（a）所示。

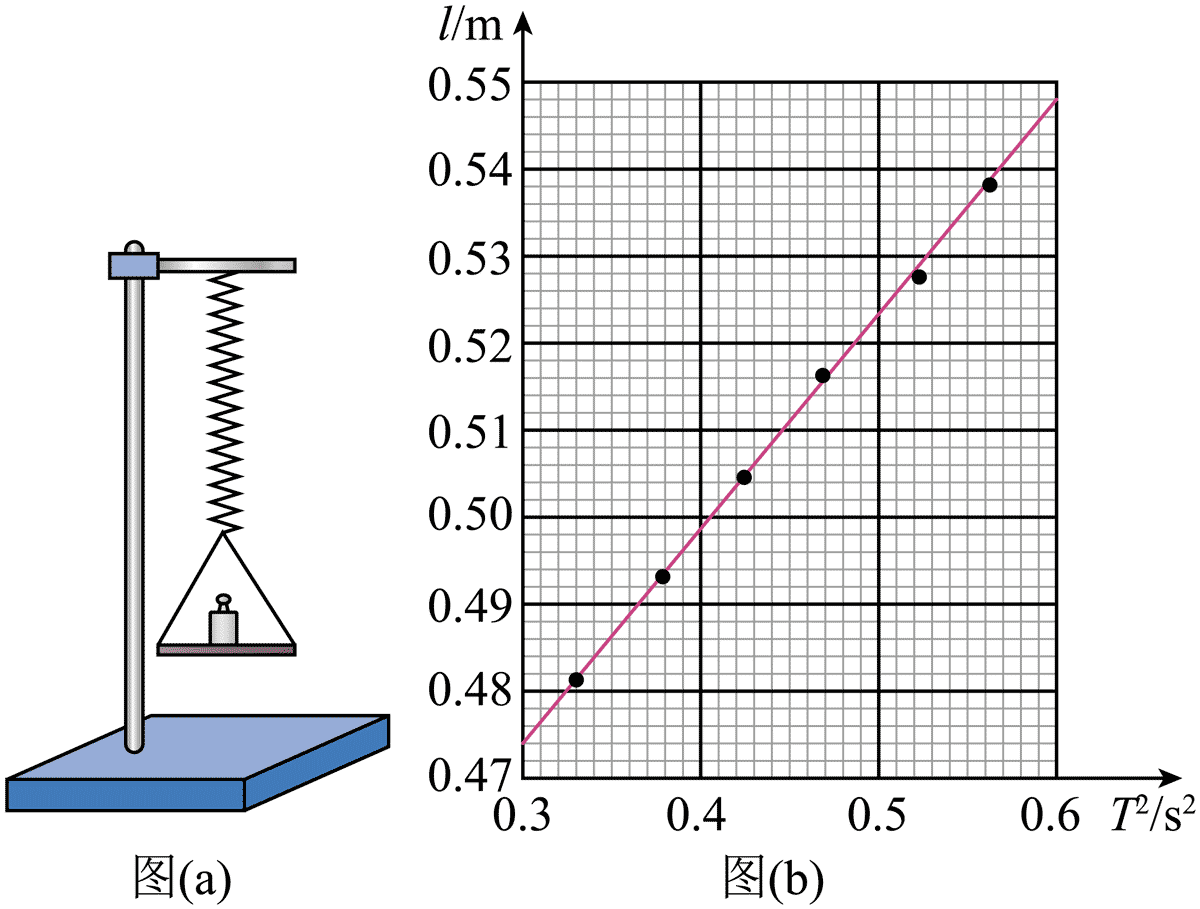
②用米尺测量平衡时弹簧的长度 l，并安装光电门。

③将弹簧在弹性限度内拉伸一定长度后释放，使其在竖直方向振动。

④用数字计时器记录 30 次全振动所用时间 t。

⑤逐次增加托盘内砝码的数量，重复②③④的操作。

该同学将振动系统理想化为弹簧振子。已知弹簧振子的振动周期 T = 2π\(\sqrt {\frac{M}{k}} \)，其中 k 为弹簧的劲度系数，M 为振子的质量。

（1）由步骤④，可知振动周期 T =_____。

（2）设弹簧的原长为 l₀，则 l 与 g、l₀、T 的关系式为 l = _____。

（3）由实验数据作出的 l – T² 图线如图（b）所示，可得 g =_____m/s²（保留三位有效数字，π² 取 9.87）。

（4）本实验的误差来源包括_____（双选，填标号）。

A．空气阻力

B．弹簧质量不为零

C．光电门的位置稍微偏离托盘的平衡位置

【答案】

（1）\(\frac{t}{{30}}\)

（2）l₀ + \(\frac{{g{T^2}}}{{4{\pi ^2}}}\)

（3）9.59

（4）AC？AB?

 

13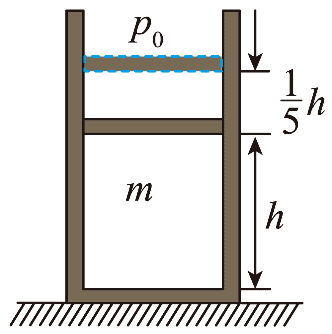．如图所示，在竖直放置、开口向上的圆柱形容器内用质量为 m 的活塞密封一部分理想气体，活塞横截面积为 S，能无摩擦地滑动。初始时容器内气体的温度为 T₀，气柱的高度为 h。当容器内气体从外界吸收一定热量后，活塞缓慢上升 \(\frac{1}{5}\)h 再次平衡。已知容器内气体内能变化量 ΔU 与温度变化量 ΔT 的关系式为 ΔU = CΔT，C 为已知常数，大气压强恒为 p₀，重力加速度大小为 g，所有温度为热力学温度。求：

（1）再次平衡时容器内气体的温度。

（2）此过程中容器内气体吸收的热量。

【答案】

（1）\(\frac{6}{5}\)T₀

（2）\(\frac{1}{5}\)(p₀S + mg)h + \(\frac{1}{5}\)CT₀

 

14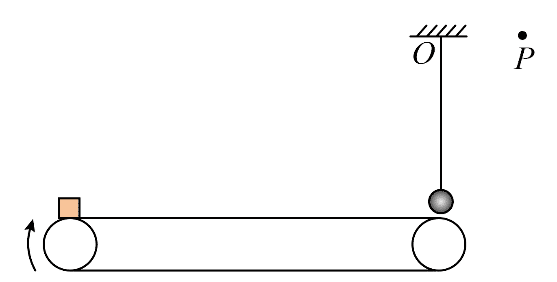．如图所示，水平传送带以 5 m/s 的速度顺时针匀速转动，传送带左右两端的距离为 3.6 m。传送带右端的正上方有一悬点 O，用长为 0.3 m、不可伸长的轻绳悬挂一质量为 0.2 kg 的小球，小球与传送带上表面平齐但不接触。在 O 点右侧的 P 点固定一钉子，P 点与 O 点等高。将质量为 0.1 kg 的小物块无初速轻放在传送带左端，小物块运动到右端与小球正碰，碰撞时间极短，碰后瞬间小物块的速度大小为 1 m/s、方向水平向左。小球碰后绕 O 点做圆周运动，当轻绳被钉子挡住后，小球继续绕 P 点向上运动。已知小物块与传送带间的动摩擦因数为 0.5，重力加速度大小 g = 10 m/s²。

（1）求小物块与小球碰撞前瞬间，小物块的速度大小；

（2）求小物块与小球碰撞过程中，两者构成的系统损失的总动能；

（3）若小球运动到 P 点正上方，绳子不松弛，求 P 点到 O 点的最小距离。

【答案】

（1）5 m/s

（2）0.3 J

（3）0.2 m

 

15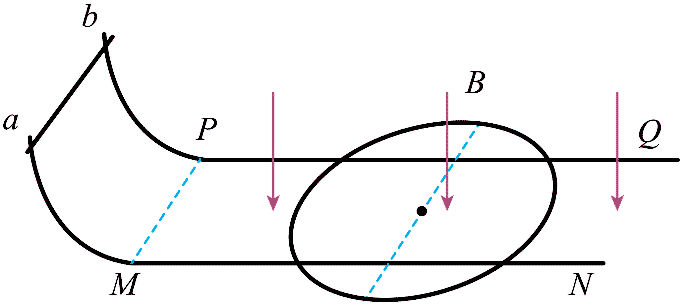．如图所示，两足够长平行金属直导轨 MN、PQ 的间距为 L，固定在同一水平面内，直导轨在左端 M、P 点分别与两条竖直固定、半径为 L 的 \(\frac{1}{4}\) 圆弧导轨相切。MP 连线与直导轨垂直，其左侧无磁场，右侧存在磁感应强度大小为 B、方向竖直向下的匀强磁场。长为 L、质量为 m、电阻为 R 的金属棒 ab 跨放在两圆弧导轨的最高点。质量为 2m、电阻为 6R 的均匀金属丝制成一个半径为 L 的圆环，水平放置在两直导轨上，其圆心到两直导轨的距离相等。忽略导轨的电阻、所有摩擦以及金属环的可能形变，金属棒、金属环均与导轨始终接触良好，重力加速度大小为 g。现将金属棒 ab 由静止释放，求：

（1）ab 刚越过 MP 时产生的感应电动势大小；

（2）金属环刚开始运动时的加速度大小；

（3）为使 ab 在整个运动过程中不与金属环接触，金属环圆心初始位置到 MP 的最小距离。

【答案】

（1）BL\(\sqrt {2gL} \)

（2）\(\frac{{{B^2}{L^2}\sqrt {2gL} }}{{3mR}}\)

（3）L + \(\frac{{mR\sqrt {2gL} }}{{{B^2}{L^2}}}\)