1．“祝融号”火星车沿如图所示路线行驶，在此过程中揭秘了火星乌托邦平原浅表分层结构，该研究成果被列为“2022 年度中国科学十大进展”之首。“祝融号”从着陆点 O 处出发，经过 61 天到达 M 处，行驶路程为 585 米；又经过 23 天，到达 N 处，行驶路程为 304 米。已知 O、M 间和 M、N 间的直线距离分别约为 463 米和 234 米，则火星车（    ）

A．从 O 处行驶到 N 处的路程为 697 米

B．从 O 处行驶到 N 处的位移大小为 889 米

C．从 O 处行驶到 M 处的平均速率约为 20 米/天

D．从 M 处行驶到 N 处的平均速度大小约为 10 米/天

【答案】

D

 

2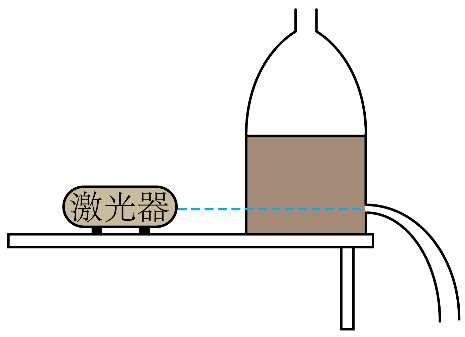．如图，一教师用侧面开孔的透明塑料瓶和绿光激光器演示“液流导光”实验。瓶内装有适量清水．水从小孔中流出后形成了弯曲的液流。让激光水平射向小孔，使光束与液流保持在同一竖直平面内，观察到光束沿着弯曲的液流传播。下列操作中，有助于光束更好地沿液流传播的是（    ）

A．减弱激光强度

B．提升瓶内液面高度

C．改用折射率更小的液体

D．增大激光器与小孔之间的水平距离

【答案】

B

【解析】

若想使激光束完全被限制在液流内，则应使激光在液体内发生全反射现象，根据全反射可知应该增大液体的折射率或则增大激光束的入射角。

A．减弱激光的强度，激光的临界角，折射率均不会改变，故 A 错误；

B．提升瓶内液面的高度，会造成开口处压强增大，水流的速度增大，水流的更远，进而增大了激光束的入射角，则会有大部分光在界面处发生全反射，有助于光速更好的沿液流传播，故 B 正确；

C．若改用折射率更小的液体，临界角变大，更不容易发生全反射，故 C 错误；

D．增大激光器与小孔之间的水平距离不能改变液体的折射率或激光束的入射角，现象不会改变，故 D 错误。

故选 B。

 

3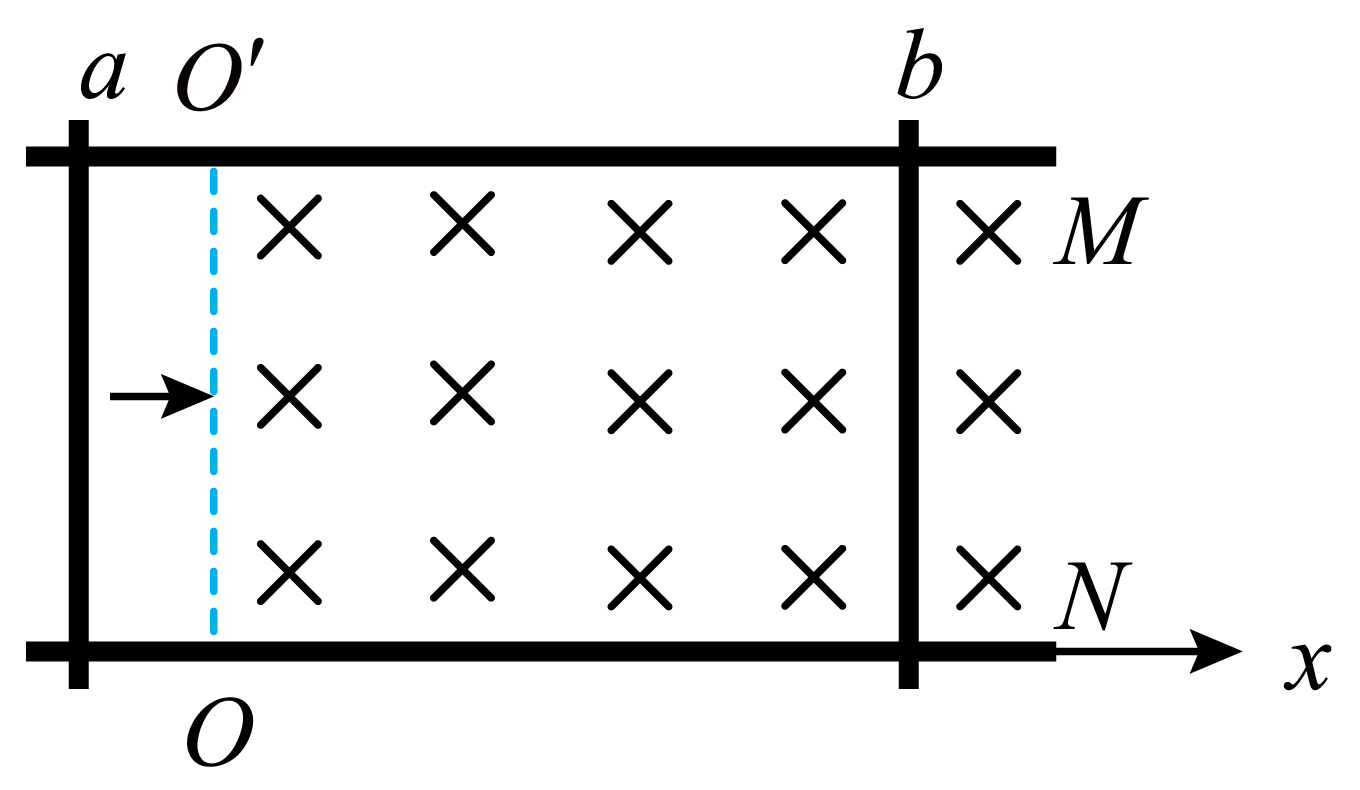．如图，M、N 是两根固定在水平面内的光滑平行金属导轨，导轨足够长且电阻可忽略不计；导轨间有一垂直于水平面向下的匀强磁场，其左边界 OOʹ 垂直于导轨；阻值恒定的两均匀金属棒 a、b 均垂直于导轨放置，b 始终固定。a 以一定初速度进入磁场，此后运动过程中始终与导轨垂直且接触良好，并与 b 不相碰。以 O 为坐标原点，水平向右为正方向建立轴坐标；在运动过程中，a 的速度记为 v，a 克服安培力做功的功率记为 P。下列 v 或 P 随 x 变化的图像中，可能正确的是（    ）

【答案】

A

 

5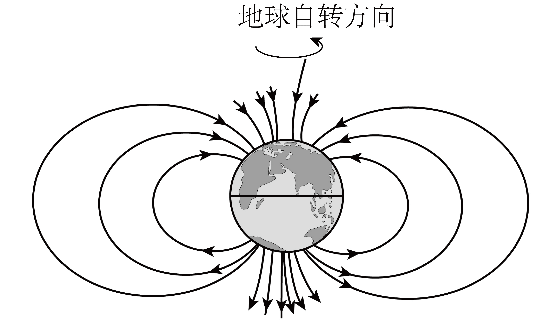．地球本身是一个大磁体，其磁场分布示意图如图所示。学术界对于地磁场的形成机制尚无共识。一种理论认为地磁场主要源于地表电荷随地球自转产生的环形电流。基于此理论，下列判断正确的是（    ）

A．地表电荷为负电荷

B．环形电流方向与地球自转方向相同

C．若地表电荷的电量增加，则地磁场强度增大

D．若地球自转角速度减小，则地磁场强度增大

【答案】

AC

【解析】

A．根据右手螺旋定则可知，地表电荷为负电荷，故 A 正确；

B．由于表电荷为负电荷，则环形电流方向与地球自转方向相反，故 B 错误；

C．若地表电荷的电量增加，则等效电流越大，地磁场强度增大，故 C 正确；

D．若地球自转角速度减小，则等效电流越小，地磁场强度减小，故 D 错误。

故选 AC。

 

6．甲、乙两辆完全相同的小车均由静止沿同一方向出发做直线运动。以出发时刻为计时零点，甲车的速度–时间图像如图（a）所示，乙车所受合外力–时间图像如图（b）所示。则（    ）

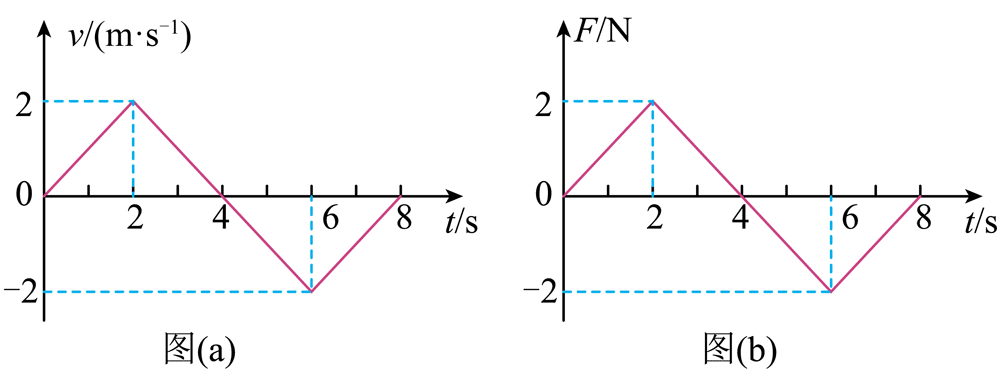
A．0 ~ 2 s 内，甲车的加速度大小逐渐增大

B．乙车在 t = 2 s 和 t = 6 s 时的速度相同

C．2 ~ 6 s 内，甲、乙两车的位移不同

D．t = 8 s 时，甲、乙两车的动能不同

【答案】

BC

【解析】

A．由题知甲车的速度–时间图像如图（a）所示，则根据图（a）可知 0 ~ 2 s 内，甲车做匀加速直线运动，加速度大小不变，故 A 错误；

B．由题知乙车所受合外力–时间图像如图（b）所示，则乙车在 0 ~ 2 s 内根据动量定理有

I₂ = mv₂，I₂ = S_{0 ~ 2} = 2 N·s

乙车在 0 ~ 6 s 内根据动量定理有

I₆ = mv₆，I₆ = S_{0 ~ 6} = 2 N·s

则可知乙车在 t = 2  s和 t = 6 s 时的速度相同，故 B 正确；

C．根据图（a）可知，2 ~ 6 s 内甲车的位移为 0；根据图（b）可知，2 ~ 6 s 内乙车一直向正方向运动，则 2 ~ 6 s 内，甲、乙两车的位移不同，故 C 正确；

D．根据图（a）可知，t = 8 s 时甲车的速度为 0，则 t = 8 s 时，甲车的动能为 0；乙车在 0 ~ 8 s 内根据动量定理有

I₈ = mv₈，I₈ = S_{0 ~ 8} = 0

可知 t = 8 s 时乙车的速度为 0，则 t = 8 s 时，乙车的动能为 0，故 D 错误。

故选 BC。

 

7．人类为探索宇宙起源发射的韦伯太空望远镜运行在日地延长线上的拉格朗日 L₂ 点附近，L₂ 点的位置如图所示。在 L₂ 点的航天器受太阳和地球引力共同作用，始终与太阳、地球保持相对静止。考虑到太阳系内其他天体的影响很小，太阳和地球可视为以相同角速度围绕日心和地心连线中的一点 O（图中未标出）转动的双星系统。若太阳和地球的质量分别为 M 和 m，航天器的质量远小于太阳、地球的质量，日心与地心的距离为 R，万有引力常数为 G，L₂ 点到地心的距离记为 r（r ≪ R），在 L₂ 点的航天器绕 O 点转动的角速度大小记为 ω。下列关系式正确的是（   ）[可能用到的近似 \(\frac{1}{{{{(R + r)}^2}}}\) ≈ \(\frac{1}{{{R^2}}}\left( {1 - 2\frac{r}{R}} \right)\)]

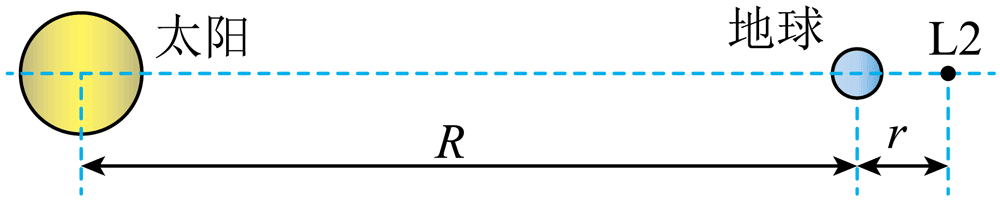
A．ω = \(\sqrt {\frac{{G(M + m)}}{{2{R^3}}}} \)                B．ω = \(\sqrt {\frac{{G(M + m)}}{{{R^3}}}} \)

C．r = \(\sqrt[3]{{\frac{{3m}}{{3M + m}}}}\) R                 D．r = \(\sqrt[3]{{\frac{{m}}{{3M + m}}}}\) R

【答案】

BD

 

9．福建福清核电站采用我国完全自主研发的“华龙一号”反应堆技术，建设了安全级别世界最高的机组。机组利用 ²³⁵U 核裂变释放的能量发电，典型的核反应方程为¹₀n + ²³⁵₉₂U→¹⁴¹_ZBa + ^A₃₆Kr + 3¹₀n，则 A = _________；Z = _________；若核反应过程中质量亏损 1 g，释放的能量为_________J。（光速大小取 3.0×10⁸ m/s）

【答案】

92，56，9×10¹³

【解析】

（1）根据核反应前后质量数守恒有 1 + 235 = 141 + A + 3

解得 A = 92

（2）根据核反应前后电荷数守恒有

92 = Z + 36

解得

Z = 56

（3）根据爱因斯坦质能方程可知核反应过程中质量亏损 1 g，释放的能量为

E = Δmc² = 1×10⁻³×9.0×10¹⁶ J = 9×10¹³ J

 

10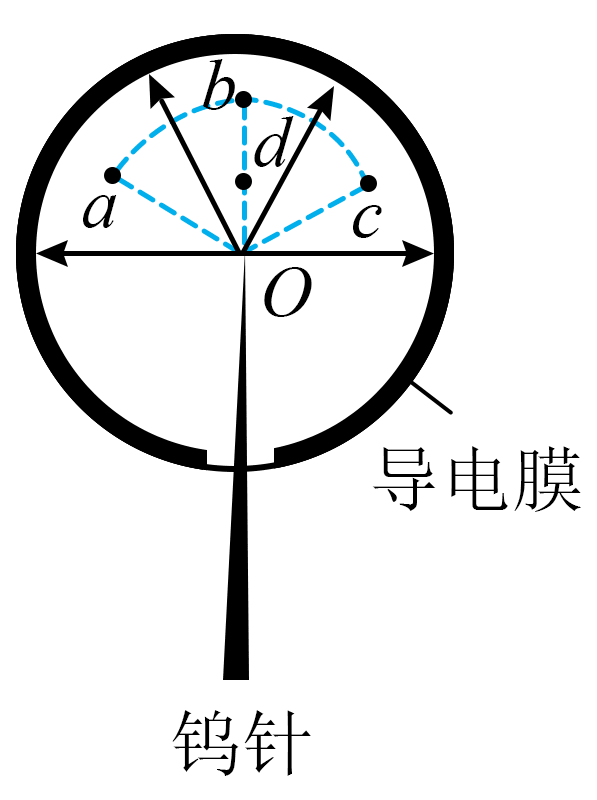．“场离子显微镜”的金属钨针尖处于球形真空玻璃泡的球心 O，玻璃泡内壁有一层均匀导电膜：在钨针和导电膜间加上高电压后，玻璃泡上半部分的电场可视为位于 O 点处点电荷形成的电场，如图所示。a、b、c、d、O 为同一平面上的 5 个点，abc 是一段以 O 为圆心的圆弧，d 为 Ob 的中点。a、d 两点场强大小分别为 E_a、E_d，O、a、c、d 四点电势分别为 φ_o、φ_a、φ_c、φ_d，则 φ_a_________φ_d；φ_a_________φ_c，(φ_o − φ_a)_________2(φ_o − φ_d)。（填“大于”“等于”或“小于”）

【答案】

小于，等于，小于

【解析】

（1）由于沿着电场线方向电势逐渐降低，可知 φ_a < φ_d

（2）（3）由题知，在钨针和导电膜间加上高电压后，玻璃泡上半部分的电场可视为位于 O 点处点电荷形成的电场，则根据点电荷形成的电场的电势分布可知

φ_a = φ_c

且越靠近 O 场强越强，则 Od 部分的场强均大于 db 部分的场强，则根据 U = Ed，结合微元法可定性判别出 φ_o − φ_b < 2(φ_o − φ_d)

而 φ_a = φ_b

则 φ_o − φ_a < 2(φ_o − φ_d)

 

11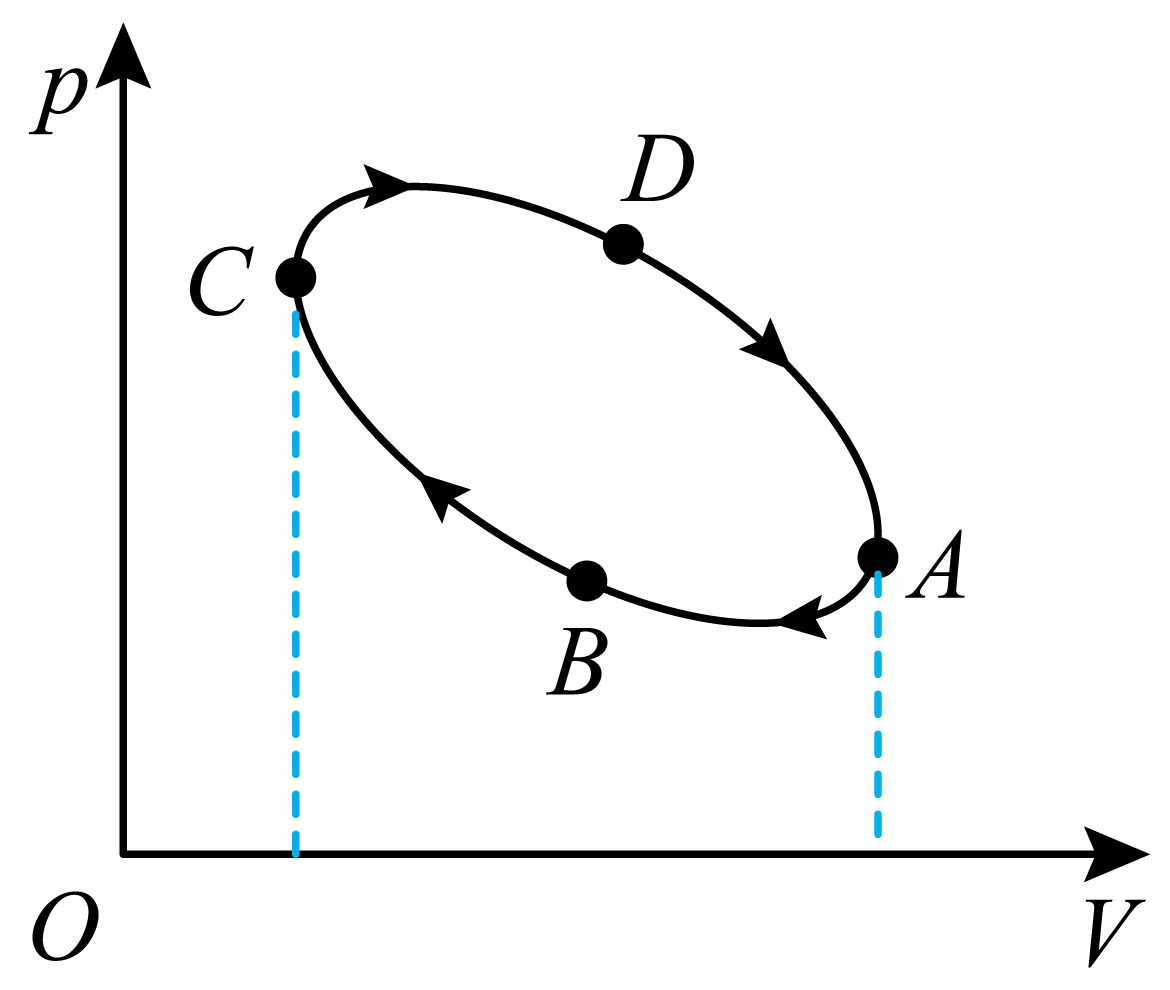．一定质量的理想气体经历了 A→B→C→D→A 的循环过程后回到状态 A，其 p – V 图如图所示。完成一次循环，气体内能_________（填“增加”“减少”或“不变”），气体对外界_________（填“做正功”“做负功”或“不做功”），气体______（填“吸热”“放热”“不吸热”或“不放热”）。

【答案】

不变，做正功，吸热

【解析】

（1）完成一次循环，回到初始状态，理想气体温度不变，而一定质量的气体的内能仅由温度决定，所以整个过程气体的内能不变；

（2）（3）对 p – V 图像来说，图像与坐标轴所围图形的面积表示气体做功情况，其中从 A→B→C 的过程气体的体积减小是外界对气体做功的过程，从 C→D→A 的过程气体的体积增大，是气体对外做功的过程，且从 C→D→A 的过程图像与坐标轴所围的面积大于从 A→B→C 的过程图像与坐标轴所围的面积，即气体对外做的功大于外界对气体做的功，则整个过程中表现为气体对外界做正功；根据热力学第一定律

ΔU = W + Q

因为 ΔU = 0，可知因 W < 0，则 Q > 0。

所以气体从外界吸收热量。

 

12．某小组用图（a）所示的实验装置探究斜面倾角是否对动摩擦因数产生影响。所用器材有：绒布木板、滑块、挡光片、米尺、游标卡尺、光电门、倾角调节仪等。实验过程如下：

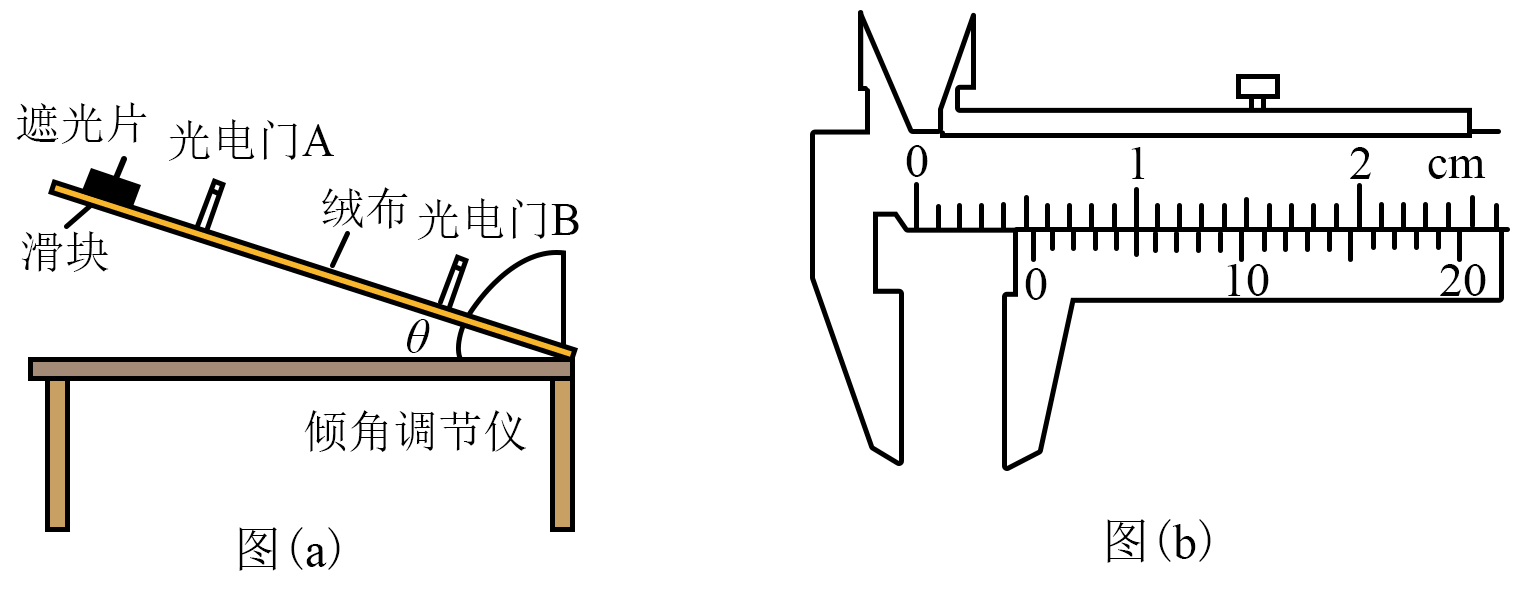
（1）将绒布平铺并固定在木板上，然后将光电门 A、B 固定在木板上。用米尺测量 A、B 间距离 L；

（2）用游标卡尺测量挡光片宽度 d，示数如图（b）所示。该挡光片宽度 d = ________mm；

（3）调节并记录木板与水平面的夹角 θ，让装有挡光片的滑块从木板顶端下滑。记录挡光片依次经过光电门 A 和 B 的挡光时间 Δt_A 和 Δt_B，求得挡光片经过光电门时滑块的速度大小 v_A 和 v_B。某次测得 Δt_A = 5.25×10⁻³ s，则 v_A = _________m/s（结果保留 3 位有效数字）

（4）推导滑块与绒布间动摩擦因数 μ 的表达式，可得 μ = _________（用 L、v_A、v_B、θ 和重力加速度大小 g 表示），利用所得实验数据计算出 μ 值；

（5）改变 θ 进行多次实验，获得与 θ 对应的 μ，并在坐标纸上作出 μ – θ 关系图像，如图（c）所示；

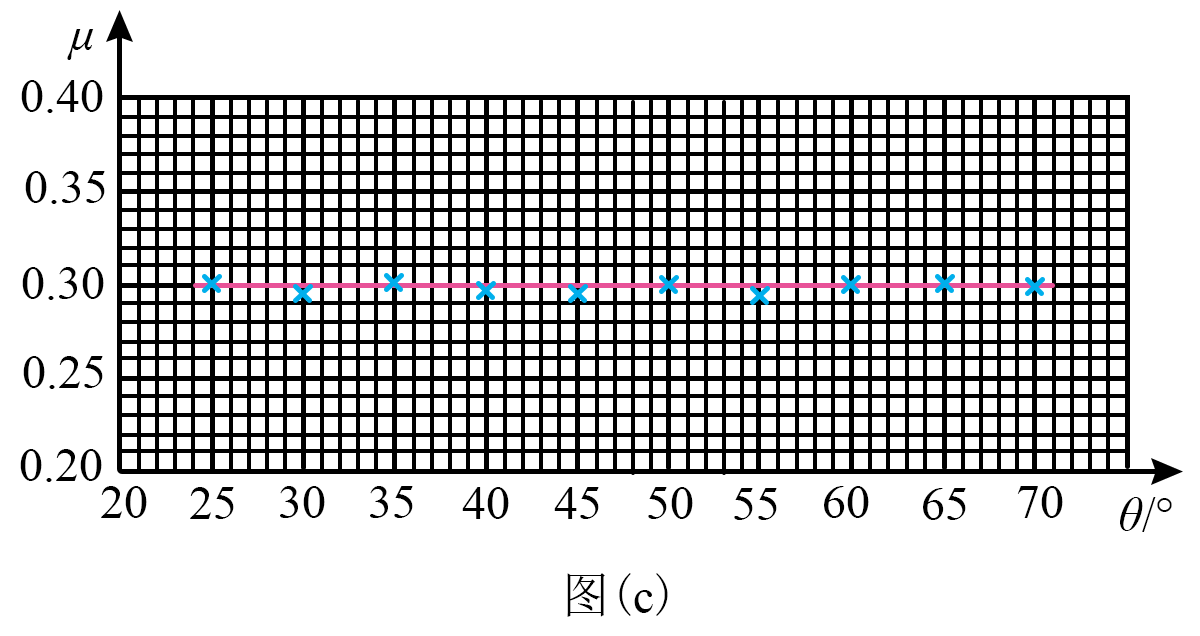
（6）根据上述实验，在误差允许范围内，可以得到的结论为_________。

【答案】

（2）5.25

（3）1.00

（4）tanθ − \(\frac{{v_{\rm{B}}^2 - v_{\rm{A}}^2}}{{2gL\cos \theta }}\)

（6）斜面倾角对动摩擦因数没有影响

 

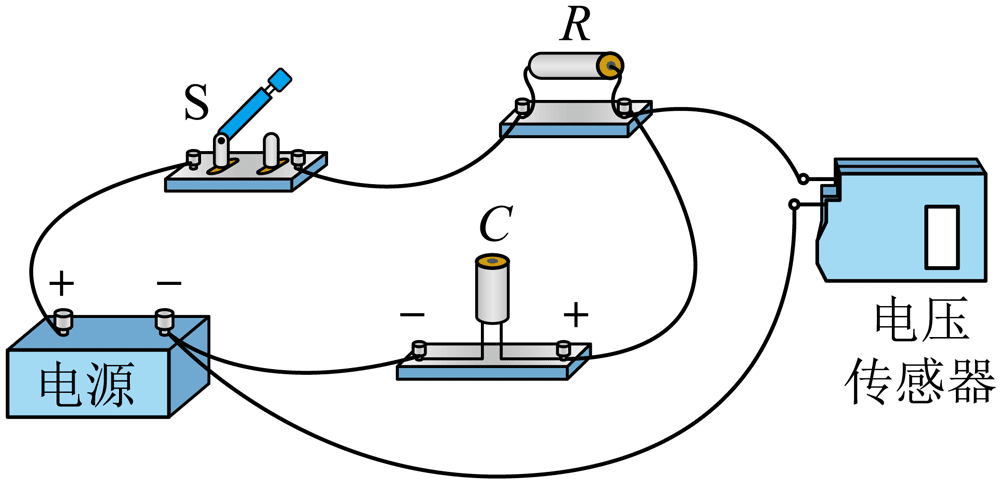
13．某同学用图（a）所示的电路观察矩形波频率对电容器充放电的影响。所用器材有：电源、电压传感器、电解电容器 C（4.7 μF，10 V），定值电阻 R（阻值 2.0 kΩ）、开关 S、导线若干。

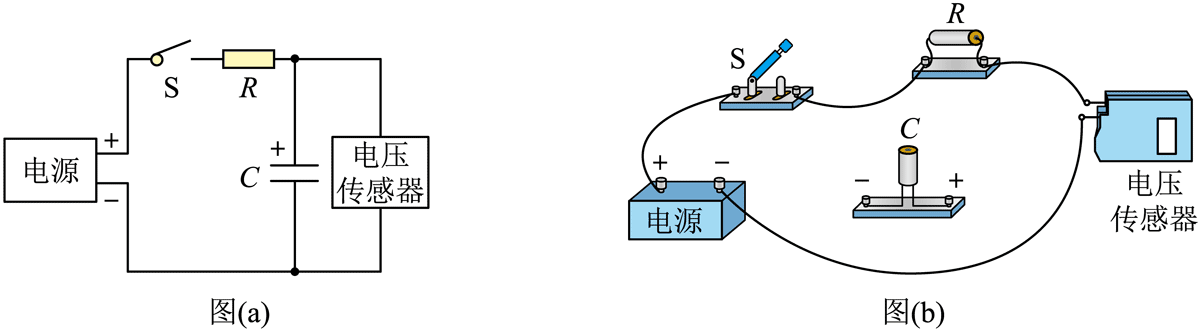
（1）电解电容器有正、负电极的区别。根据图（a），将图（b）中的实物连线补充完整_________；

（2）设置电源，让电源输出图（c）所示的矩形波，该矩形波的频率为_________Hz；

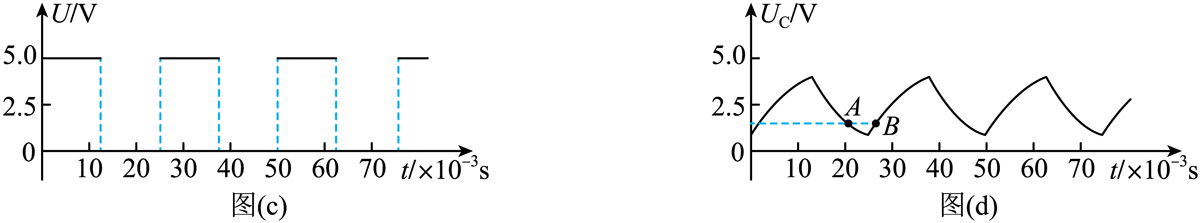
（3）闭合开关S，一段时间后，通过电压传感器可观测到电容器两端的电压 U_C 随时间周期性变化，结果如图（d）所示，A、B 为实验图线上的两个点。在 B 点时，电容器处于_________状态（填“充电”或“放电”）在_________点时（填“A”或“B”），通过电阻 R 的电流更大；

（4）保持矩形波的峰值电压不变，调节其频率，测得不同频率下电容器两端的电压随时间变化的情况，并在坐标纸上作出电容器上最大电压 U_m 与频率 f 关系图像，如图（e）所示。当 f = 45 Hz 时电容器所带电荷量的最大值 Q_m = _________C（结果保留两位有效数字）；

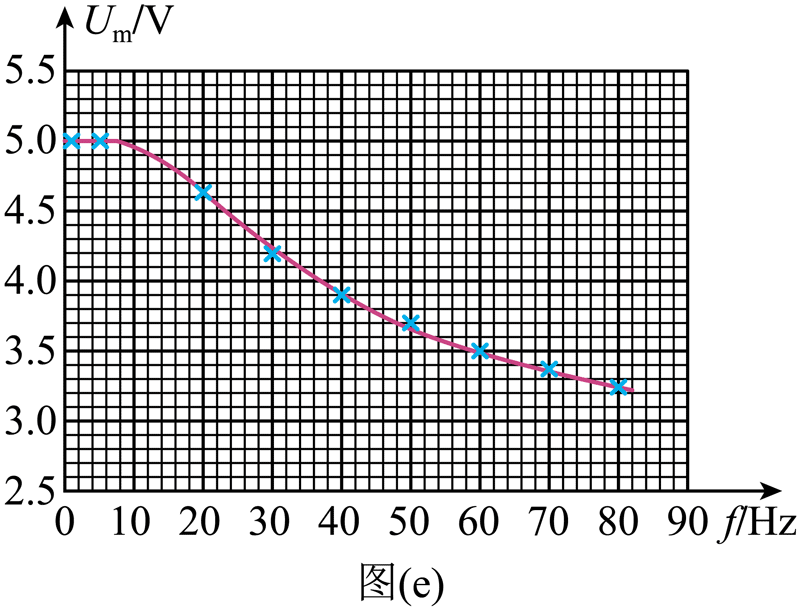
（5）根据实验结果可知，电容器在充放电过程中，其所带的最大电荷量在频率较低时基本不变，而后随着频率的增大逐渐减小。

【答案】

（1）

（2）40

（3）充电，B

（4）1.8×10⁻⁵

 

14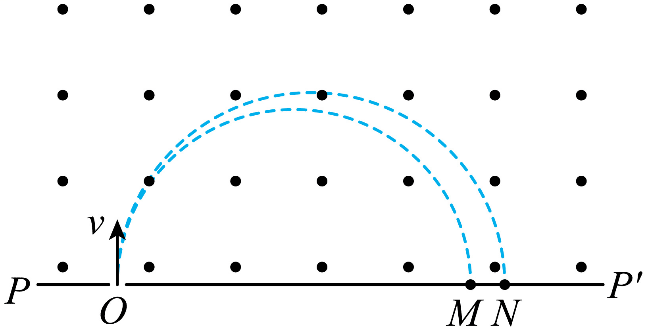．阿斯顿（F．Aston）借助自己发明的质谱仪发现了氖等元素的同位素而获得诺贝尔奖，质谱仪分析同位素简化的工作原理如图所示。在 PPʹ 上方存在一垂直纸面向外的匀强磁场，磁感应强度大小为 B。两个氖离子在 O 处以相同速度 v 垂直磁场边界入射，在磁场中发生偏转，分别落在 M 和 N 处。已知某次实验中，v = 9.6×10⁴ m/s，B = 0.1 T，落在 M 处氖离子比荷（电荷量和质量之比）为 4.8×10⁶ C/kg；P、O、M、N、Pʹ 在同一直线上；离子重力不计。

（1）求 OM 的长度；

（2）若 ON 的长度是 OM 的 1.1 倍，求落在 N 处氖离子的比荷。

【答案】

（1）0.4 m

（2）4.4×10⁶ C/kg

 

15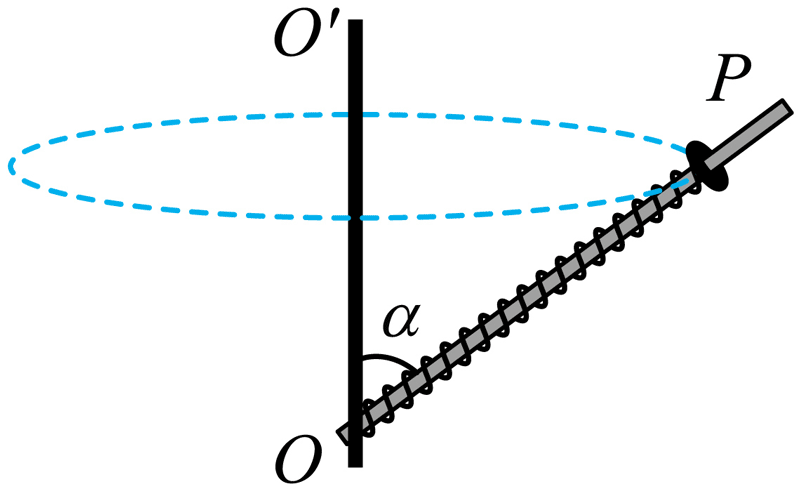．一种离心测速器的简化工作原理如图所示。细杆的一端固定在竖直转轴 OOʹ 上的 O 点，并可随轴一起转动。杆上套有一轻质弹簧，弹簧一端固定于 O 点，另一端与套在杆上的圆环相连。当测速器稳定工作时，圆环将相对细杆静止，通过圆环的位置可以确定细杆匀速转动的角速度。已知细杆长度 L = 0.2 m，杆与竖直转轴的夹角 α 始终为 60°，弹簧原长 x₀ = 0.1 m，弹簧劲度系数 k = 100 N/m，圆环质量 m = 1 kg；弹簧始终在弹性限度内，重力加速度大小取 10 m/s²，摩擦力可忽略不计。

（1）若细杆和圆环处于静止状态，求圆环到 O 点的距离；

（2）求弹簧处于原长时，细杆匀速转动的角速度大小；

（3）求圆环处于细杆末端 P 时，细杆匀速转动的角速度大小。

【答案】

（1）0.05 m

（2）\(\frac{{10\sqrt 6 }}{3}\) rad/s

（3）10 rad/s

 

16．如图（a），一粗糙、绝缘水平面上有两个质量均为 m 的小滑块 A 和 B，其电荷量分别为 q(q > 0)和 − q。A 右端固定有轻质光滑绝缘细杆和轻质绝缘弹簧，弹簧处于原长状态。整个空间存在水平向右场强大小为 E 的匀强电场。A、B 与水平面间的最大静摩擦力等于滑动摩擦力，其大小均为 2qE。t = 0 时，A 以初速度 v₀ 向右运动，B 处于静止状态。在 t₁ 时刻，A 到达位置 S，速度为 v₁，此时弹簧未与 B 相碰；在 t₂ 时刻，A 的速度达到最大，此时弹簧的弹力大小为 3qE；在细杆与 B 碰前的瞬间，A 的速度为 2v₁，此时 t = t₃。0 ~ t₃ 时间内 A 的 v – t 图像如图（b）所示，v₁ 为图线中速度的最小值，t₁、t₂、t₃ 均为未知量。运动过程中，A、B 处在同一直线上，A、B 的电荷量始终保持不变，它们之间的库仑力等效为真空中点电荷间的静电力，静电力常量为 k；B 与弹簧接触瞬间没有机械能损失，弹簧始终在弹性限度内。

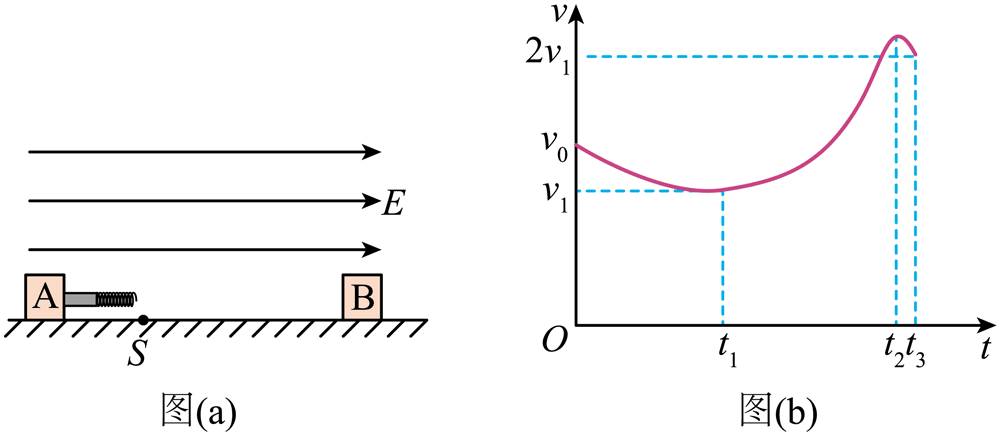
（1）求 0 ~ t₁ 时间内，合外力对 A 所做的功；

（2）求 t₁ 时刻 A 与 B 之间的距离；

（3）求 t₁ ~ t₂ 时间内，匀强电场对 A 和 B 做的总功；

（4）若增大 A 的初速度，使其到达位置 S 时的速度为 2v₁，求细杆与 B 碰撞前瞬间 A 的速度。

【答案】

（1）\(\frac{1}{2}\)mv₁² − \(\frac{1}{2}\)mv₀²

（2）\(\sqrt {\frac{{kq}}{E}} \)

（3）\(\frac{{q\sqrt {kqE} }}{2}\)

（4）(1 + \(\sqrt 3 \))v₁