1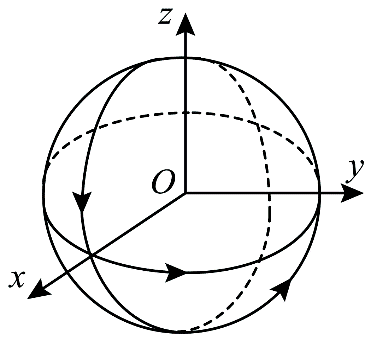．如图，球心在坐标原点 O 的球面上有三个彼此绝缘的金属环，它们分别与 x – y 平面、y – z 平面、z – x 平面与球面的交线（大圆）重合，各自通有大小相等的电流，电流的流向如图中箭头所示，坐标原点处的磁场方向与 x 轴、y 轴、z 轴的夹角分别是（    ）

A．− arccos\(\frac{1}{{\sqrt 3 }}\)，− arccos\(\frac{1}{{\sqrt 3 }}\)，− arccos\(\frac{1}{{\sqrt 3 }}\)

B．arccos\(\frac{1}{{\sqrt 3 }}\)，− arccos\(\frac{1}{{\sqrt 3 }}\)，− arccos\(\frac{1}{{\sqrt 3 }}\)

C．arccos\(\frac{1}{{\sqrt 3 }}\)，arccos\(\frac{1}{{\sqrt 3 }}\)，− arccos\(\frac{1}{{\sqrt 3 }}\)

D．arccos\(\frac{1}{{\sqrt 3 }}\)，arccos\(\frac{1}{{\sqrt 3 }}\)，arccos\(\frac{1}{{\sqrt 3 }}\)

【答案】

D

 

2．从楼顶边缘以大小为 v₀ 的初速度竖直上抛一小球；经过 t₀ 时间后在楼顶边缘从静止开始释放另一小球．若要求两小球同时落地，忽略空气阻力，则 v₀ 的取值范围和抛出点的高度应为（    ）

A．\(\frac{1}{2}\)gt₀ ≤ v₀ < gt₀，h = \(\frac{1}{2}gt_0^2{\left( {\frac{{{v_0} - g{t_0}}}{{{v_0} - \frac{1}{2}g{t_0}}}} \right)^2}\)

B．v₀ ≠ gt₀，h = \(\frac{1}{2}gt_0^2{\left( {\frac{{{v_0} - \frac{1}{2}g{t_0}}}{{{v_0} - g{t_0}}}} \right)^2}\)

C．\(\frac{1}{2}\)gt₀ ≤ v₀ < gt₀，h = \(\frac{1}{2}gt_0^2{\left( {\frac{{{v_0} - \frac{1}{2}g{t_0}}}{{{v_0} - g{t_0}}}} \right)^2}\)

D．v₀ ≠ \(\frac{1}{2}\)gt₀，h = \(\frac{1}{2}gt_0^2{\left( {\frac{{{v_0} - g{t_0}}}{{{v_0} - \frac{1}{2}g{t_0}}}} \right)^2}\)

【答案】

C

 

3．如图，四个半径相同的小球（构成一个体系）置于水平桌面的一条直线上，其中一个是钕永磁球（标有北极 N 和南极 S），其余三个是钢球；钕球与右边两个钢球相互接触．让另一钢球在钕球左边一定距离处从静止释放，逐渐加速，直至与钕球碰撞，此时最右边的钢球立即以很大的速度被弹开。对于整个过程的始末，下列说法正确的是（    ）

A．体系动能增加，体系磁能减少            B．体系动能减少，体系磁能增加

C．体系动能减少，体系磁能减少            D．体系动能增加，体系磁能增加

【答案】

A

 

4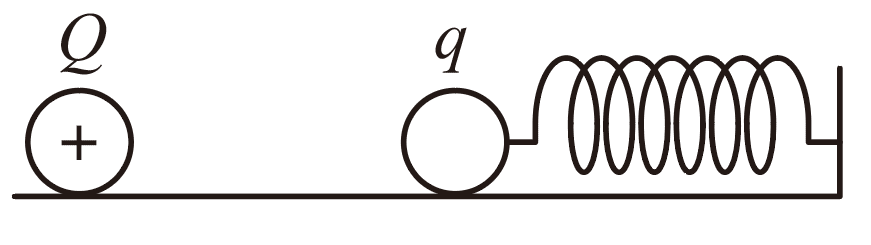．如图，一带正电荷 Q 的绝缘小球（可视为点电荷）固定在光滑绝缘平板上，另一绝缘小球（可视为点电荷）所带电荷用（其值可任意选择）表示，可在平板上移动，并连在轻弹簧的一端，轻弹簧的另一端连在固定挡板上；两小球的球心在弹簧的轴线上。不考虑可移动小球与固定小球相互接触的情形，且弹簧的形变处于弹性限度内。关于可移动小球的平衡位置，下列说法正确的是（    ）

A．若 q > 0，总有一个平衡的位置

B．若 q > 0，没有平衡位置

C．若 q < 0，可能有一个或两个平衡位置

D．若 q < 0，没有平衡位置

【答案】

AC

 

5．如图，小物块 a、b 和 c 静置于光滑水平地面上。现让 a 以速度 v 向右运动，与 b 发生弹性正碰，然后 b 与 c 也发生弹性正碰。若 b 和 c 的质量可任意选择，碰后 c 的最大速度接近于（    ）

A．2v            B．3v            C．4v            D．5v

【答案】

C

 

6．2016 年 2 月 11 日美国国家科学基金会宣布：美国的“激光干涉引力波天文台“（LIGO）的两台孪生引力波探测器首次直接探测到了引力波．该引力波是由 13 亿光年之外的两颗黑洞在合并的最后阶段产生的。初始质量分别为 29 倍太阳质量和 36 倍太阳质量的两颗黑洞，合并成了一颗 62 倍太阳质量、高速旋转的黑洞；亏损的质量以引力波的形式释放到宇宙空间．这亏损的质量为______kg，相当于______J 的能量．已知太阳质量约为 2.0×10³⁰ kg，光在真空中的速度为 3.0×10⁸ m/s。

【答案】

6.0×10³⁰，5.43.0×10⁴⁷

 

7．在一水平直线上相距 18 m 的 A、B 两点放置两个波源．这两个波源振动的方向平行、振幅相等、频率都是 30 Hz，且有相位差 π。它们沿同一条直线在其两边的媒质中各激起简谱横波。波在媒质中的传播速度为 360 m/s。这两列波在 A、B 两点所在直线上因干涉而振幅等于原来各自振幅的点有______个，它们到 A 点的距离依次为______________m。

【答案】

6；2.0，4.0，8.0，10，14，16

 

8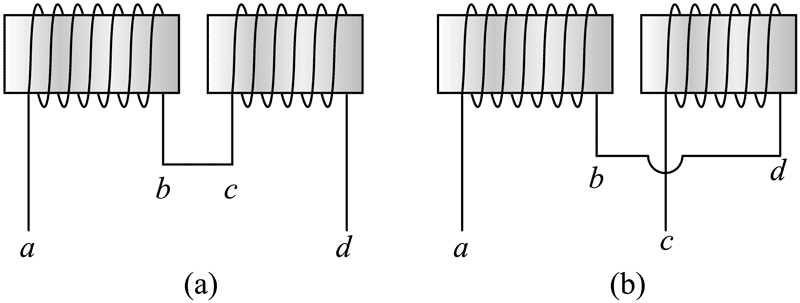．如图，以 a、b 为端点的线圈 1 的自感为 L₁，以 c、d 为端点的线圈 2 的自感为 L₂，互感为 M（线圈 1 中的电流的变化在线圈 2 中产生的感应电动势与线圈中电流随时间的变化率成正比，比例系数称为互感 M₂₁；且 M₁₂ = M₂₁ = M）。若将两线圈 1 和 2 首尾相连（顺接）而串联起来，如图（a）所示，则总自感为______；若将两线圈 1 和 2 尾尾相接（反接）而串联起来，如图（b）所示，则总自感为______。

【答案】

L₁ + L₂ + 2M，L₁ + L₂ − 2M

 

9．如图，一小角度单摆的轻质摆杆的长度 AB = L，地球半径 OC = R，单摆的悬点到地面的距离 AC = L。已知地球质量为 M，引力常量为 G。当 L ≪ R 时，单摆做简谐运动的周期为______；当 L ≫ R 时，单摆做简谐运动的周期为______。悬点相对于地球不动，不考虑地球自转。

【答案】

2π\(\sqrt {\frac{{L{R^2}}}{{MG}}} \)，2π\(\sqrt {\frac{{{R^3}}}{{MG}}} \)

 

10．μ⁻ 子与电子的性质相似，其电量与电子相同，而质量 m_μ 约为电子的 206.8 倍。用 μ⁻ 子代替氢原子中的电子就形成 μ⁻ 子－氢原子，μ⁻ 子－氢原子的线状光谱与氢原子具有相似的规律。μ⁻ 子－氢原子基态的电离能为______eV，μ⁻ 子－氢原子从第二激发态跃迁到第一激发态发出的光子的波长为______Å。已知质子质量 m_p 是电子的 1 836 倍，氢原子基态的电离能为 13.605 eV；光在真空中的速度为 2.998×10⁸ m/s，普朗克常量为 4.136×10⁻¹⁵ eV·s。（按玻尔理论计算时，在 μ⁻ 子－氢原子中若仍将质子视为不动，则 μ⁻ 子相当于质量为 \(\frac{{{m_{\rm{\mu }}}{m_{\rm{p}}}}}{{{m_{\rm{\mu }}} + {m_{\rm{p}}}}}\) 的带电粒子）

【答案】

2530，35.29

 

11．一足球运动员 1 自 A 点向球门的 B 点踢出球，已知 A、B 之间的距离为 s，球自 A 向 B 的运动可视为水平地面上的匀速直线运动，速率为 u。另一足球运动员 2 到 AB 连线的距离为 l，到 A、B 两点的距离相等．运动员 1 踢出球后，运动员 2 以匀速 v 沿直线去拦截该球。设运动员 2 开始出发去拦截球的时刻与球被运动员 1 踢出的时刻相同。

（1）如果运动员 2 能拦截到球，求运动员 2 开始出发去拦截球直至拦截到球的时间间隔、球被拦截时球到 A 点的距离、球到运动员 2 出发点的距离和运动员 2 运动的方向与 A、B 连线的夹角；

（2）求为了使运动员 2 能拦截到球，u、v、s 和 l 应当满足的条件。

【答案】

略

 

12．一固体星球可近似看作半径为 R（足够大）的球形均匀的固体，构成星球的物质的密度为 ρ，引力常量为 G。

（1）考虑星球表面山体的高度．如果山高超出某一限度，山基便发生流动（可认为是山基部分物质熔化的结果，相当于超出山的最高限的那块固体物质从山顶移走了），从而使山的高度减低，山在这种情况下其高度的小幅减低可视为一小块质量的物质从山顶移至山底。假设该小块的物质重力势能的减小与其全部熔化所需要的能量相当，山体由同一种物质构成该物质的熔化热为 L，不考虑温度升到熔点所需要能量，也不考虑压强对固体熔化热的影响。试估计由同一种物质构成的山体高度的上限。

（2）若由同一种物质构成的山高的上限不大于 R/10，试估计在此条件下由同一种物质构成的星球半径的下限。

（3）月亮是一个固体星球，其密度和半径分别为 3.34×10³ kg/m³ 和 1.7×10⁶ m。假设月亮全由 SiO₂ 构成，SiO₂ 的熔化热为 2.4×10⁵ J/kg。已知 G = 6.67×10⁻¹¹ N·m²/kg²。估计月球上的山体高度与月球半径比值的上限。

【答案】

（1）h ≤ \(\frac{{3L}}{{4\pi G\rho R}}\)

（2）R ≥ \(\sqrt {\frac{{15L}}{{2\pi G\rho }}} \)

（3）0.09

 

13．真空中平行板电容器两极板的面积均为 S，相距 d，上、下极板所带电量分别为 Q 和 – Q（Q > 0）。现将一厚度为 t、面积为 S/2（宽度和原来的极板相同，长度是原来极板的一半）的金属片在上极板的正下方平行插入电容器，将电容器分成如图所示的 1、2、3 三部分。不考虑边缘效应。静电力常量为 k。试求：

（1）插入金属片以后电容器的总电容；

（2）金属片上表面所带电量；

（3）1、2、3 三部分的电场强度；

（4）插入金属片过程中外力所做的功。

【答案】

（1）C = \(\frac{S}{{8\pi k}}\left( {\frac{1}{d} + \frac{1}{{d - t}}} \right)\)

（2）\(\frac{d}{{2d - t}}\) Q

（3）E₂ = E₁ = \(\frac{{8\pi k}}{S}\frac{{Qd}}{{2d - t}}\)，E₃ = \(\frac{{8\pi k}}{S}\frac{{Q(d - t)}}{{2d - t}}\)

（4）W = − \(\frac{{2\pi k}}{S}\frac{{{Q^2}dt}}{{2d - t}}\)

 

14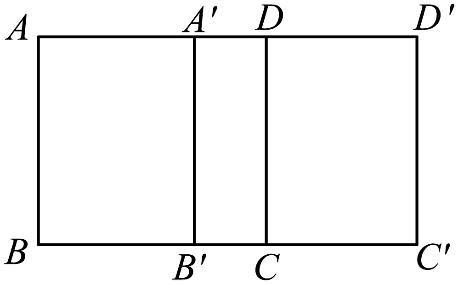．如图，两个相同的正方形刚性细金属框 ABCD 和 AʹBʹCʹDʹ 的质量均为 m，边长均为 a，每边电阻均为 R；两框部分地交叠在同一平面内，两框交叠部分长为 l，电接触良好。将整个系统置于恒定的匀强磁场中，磁感应强度大小为 B₀，方向垂直于框面（纸面）向纸面内。现将磁场突然撤去，求流过框边重叠部分 AʹD 的横截面的总电荷量。不计摩擦、重力和框的电感。

【答案】

Q = − \(\frac{{{a^2} + al - {l^2}}}{{3{a^2} - {l^2}}}\frac{{{B_0}{a^2}}}{R}\)

 

15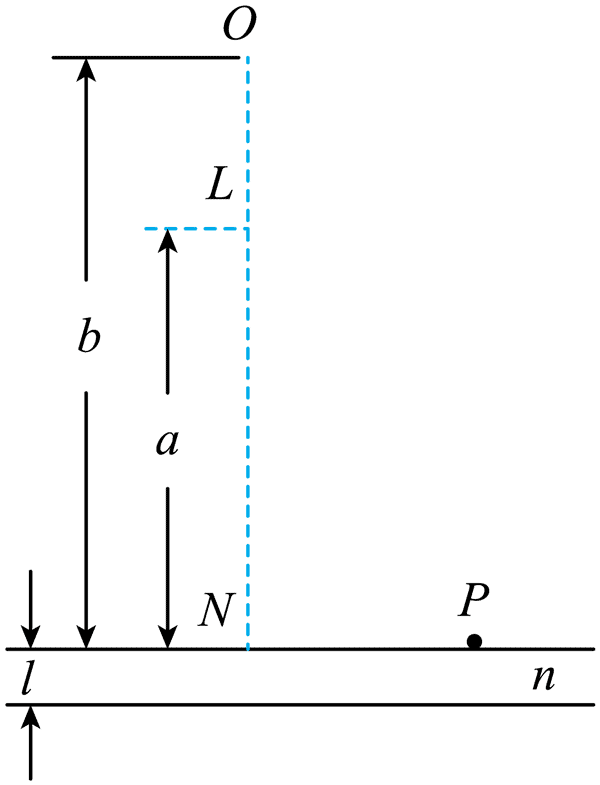．牛顿曾观察到一束细日光射到有灰尘的反射镜上面会产生干涉条纹。为了分析这一现象背后的物理，考虑如图所示的简单实验。一平板玻璃的折射率为 n，厚度为 t，下表面涂有水银反射层，上表面撒有滑石粉（灰尘粒子）。观察者 O 和单色点光源 L（光线的波长为 λ）的连线垂直于镜面（垂足为N），LN = a，ON = b。反射镜面上的某灰尘粒子 P 与直线 ON 的距离为 r（b > a ≫ r > t）。观察者可以观察到明暗相间的环形条纹 。

（1）求第 m 个亮环到 N 点的距离；

（2）若 n = 1.63，a = 0.0495 m，b = 0.245 m，t = 1.1×10⁻⁵ m，λ = 680 nm，求最小亮环（m = 1）的半径。

已知：sinx ≈ x，\(\sqrt {1 + x} \) ≈ 1 + \(\frac{x}{2}\)，当 x ≪ 1。

【答案】

（1）r = ba \(\sqrt {\frac{{mn\lambda }}{{t({b^2} - {a^{}})}}} \)

（2）r₀ = 0.016 m

 

16．充有水的连通软管常常用来检验建筑物的水平度．但软管中气泡会使得该软管两边管口水面不在同一水平面上．为了说明这一现象的物理原因，考虑如图所示的连通水管（由三管内径相同的 U 形管密接而成），其中封有一段空气（可视为理想气体），与空气接触的四段水管均在竖直方向；且两个有水的 U 形管两边水面分别等高。此时被封闭的空气柱的长度为 L_a。已知大气压强为 p₀、水的密度为 ρ、重力加速度大小为 g，L₀ ≡ \(\frac{{{p_0}}}{{\rho g}}\)。现由左管口添加体积为 ΔV = xS 的水，S 为水管的横截面积，在稳定后：

（1）求两个有水的 U 形管两边水面的高度的变化和左管添水后封闭的空气柱长度；

（2）当 x ≪ L₀、L_a ≪ L_b 时，求两个有水的 U 形管两边水面的高度的变化（用 x 表出）以及空气柱的长度。已知 \(\sqrt {1 + z} \) ≈ 1 + \(\frac{z}{2}\)，当 z ≪ 1。

【答案】

略