1．如图，弹簧振子在 A、B 之间做简谐运动，O 为平衡位置，A、B 间的距离为 20 cm，由 A 运动到 B 的最短时间为 1 s，则下列说法正确的是（    ）

A．从 O 到 A 再到 O 振子完成一次全振动

B．振子的周期为 2 s，振幅为 20 cm

C．振子完成两次全振动所通过的路程是 80 cm

D．从 A 点开始经过 2 s 时，振子对平衡位置的位移为零

【答案】

C

 

2．如图所示为一简谐运动的振动图像，则下列说法正确的是（    ）

A．该简谐运动的振幅为 6 cm，周期为 8 s

B．6 ~ 8 s 时间内，振子由负向最大位移处向平衡位置运动

C．图中的正弦函数曲线表示振子的运动轨迹

D．该振动图像对应的函数表达式为 x = 3sin\(\left( {\frac{\pi }{4}t} \right)\)

【答案】

BD

 

3．一振子沿 x 轴做简谐运动，平衡位置在坐标原点。t = 0 时振子的位移为 − 0.2 m，t = 1 s 时振子的位移为 0.2 m，则（    ）

A．若振幅为 0.2 m，振子的周期可能为 \(\frac{1}{3}\) s

B．若振幅为 0.2 m，振子的周期可能为 \(\frac{4}{5}\) s

C．若振幅为 0.4 m，振子的周期可能为 \(\frac{6}{11}\) s

D．若振幅为 0.4 m，振子的周期可能为 \(\frac{5}{13}\) s

【答案】

C

 

4．把水平的弹簧振子抽象为理想模型时，不可以忽略不计的是（    ）

A．振子所受的阻力              B．振子的形状大小

C．弹簧的质量                      D．振子的质量

【答案】

D

 

5．关于简谐运动，下列说法正确的是（    ）

A．简诣运动一定是水平方向的运动

B．所有的振动都可以看作是简谐运动

C．物体做简谐运动时的轨迹线一定是正弦函数曲线

D．只要振动图像是正弦函数曲线，物体一定做简谐运动

【答案】

 D

 

6．关于简谐运动的周期、频率、振幅，下列说法正确的是（    ）

A．振幅是矢量，方向从平衡位置指向最大位移处

B．周期和频率的乘积是一个常数

C．振幅增加，周期也必然增加，而频率减小

D．频率与振幅有关

【答案】

B

 

7．如图所示为一个质点做简谐运动的振动图像，下列说法正确的是（    ）

A．t₁ 至 t₂ 时刻质点完成一次全振动

B．t₁ 至 t₃ 时刻质点完成一次全振动

C．t₁ 至 t₄ 时刻质点完成一次全振动

D．t₂ 至 t₄ 时刻质点完成一次全振动

【答案】

C

 

8．一个质点做简谐运动，振幅为 0.8 cm，周期为 0.25 s，计时开始时具有正向最大速度，它的位移与时间的关系式为（    ）

A．x = 8×10⁻³ sin（8πt）                      B．x = 8×10⁻³cos（8πt）

C．x = 8\(\sqrt 2 \)×10⁻³sin（8πt）                D．x = 8\(\sqrt 2 \)×10⁻³cos（8πt）

【答案】

A

 

9．弹簧振子从距离平衡位置5 cm 处由静止释放，4 s 内完成 5 次全振动，则这个弹簧振子的振幅为_______cm，振动的周期为_______s；4 s 末振子的位移大小为______cm，4 s 内振子通过的路程为_______cm。

【答案】

5，0.8，5，100

 

10．如图甲所示，一个质点经过平衡位置 O，在 A、B 两点间做简谐运动，它的振动图像如图乙所示，设向右为正方向，则 OB = ________cm；第 0.7 s 末，质点位置在_______点与________点之间。

【答案】

5，O，B

 

11．有两个振动，其位移与时间的关系式分别为 x₁ = 4sin（100πt + \(\frac{\pi }{3}\)）、x₂ = 5sin（50πt + \(\frac{\pi }{3}\)），下列说法正确的是（    ）

A．两振动的振幅相同                  B．两振动的相位差恒定

C．两振动的初相位相同              D．两振动的振动步调一致

【答案】

C

 

12．如图所示为获取弹簧振子的振动图像的一种方法，改变纸带运动的速度，下列说法正确的是（    ）

A．如果纸带不动，画出的振动图像仍然是正弦函数曲线

B．如果纸带不动，画出的振动图像是一条线段

C．图示时刻，振子正经过平衡位置向左运动

D．若纸带运动的速度不恒定，则纸带上画出的仍然是简谐运动的图像

【答案】

B

 

13．如图甲所示，水平的光滑杆上有一个弹簧振子，振子以 O 点为平衡位置，在 a、b 两点之间做简谐运动，取向右为正方向，其振动图像如图乙所示。由振动图像可知（    ）

A．振子的振动周期等于 t₁

B．在 t = 0 时刻，振子的位置在 a 点

C．在 t = t₁ 时刻，振子向右经过 O 点

D．从 t₁ 到 t₂，振子正从 O 点向 a 点运动

【答案】

C

 

14．用频闪照相的方法获得弹簧振子的 x – t 图像如图所示，下列有关该图像的说法正确的是（    ）

A．该图傺的坐标原点建立在振子的平衡位置

B．从图像中可以看出振子在振动过程中是沿 t 轴方向移动的

C．为了显示振子在不同时刻偏离平衡位置的位移，让底片沿垂直 x 轴方向匀速运动

D．图像中振子的疏密显示出相同时间内振子位置变化的快慢不同

【答案】

ACD

 

15．一弹簧振子做简谐运动，振幅为 A，周期为 T，下列说法正确的是（    ）

A．若 t 时刻和 t + Δt 时刻振子对平衡位置的位移大小相等，方向相同，则 Δt 一定等于 T 的整数倍

B．t 时刻和 t + \(\frac{T}{2}\) 时刻振子对平衡位置的位移一定等大反向（位移为零时除外）

C．在 \(\frac{T}{2}\) 时间内，质点的路程一定为 2A

D．若 Δt = \(\frac{T}{4}\)，则 t 和 t + Δt 两时刻，振子的位移大小之和一定等于 A

【答案】

BC

 

16．某质点在竖直方向上做简谐运动，规定竖直向上为正方向，质点的振动图像如图所示，则质点在 10 s 时刻的速度方向______________（选填“竖直向上”或“竖直向下”），0.5 ~ 1.5 s 时间内的位移为__________cm，0 ~ \(\frac{{15}}{4}\) s 内运动的路程为_________cm。

【答案】

竖直向上，− 80，320 − 20

 

17．一个质点在平衡位置 O 附近做简谐运动，它离开 O 点运动后经过 3 s 第一次经过 M 点，再经过 2 s 第二次经过 M 点，则该质点的振动周期为_________s。若该质点由 O 点出发后在 20 s 内经过的路程是 20 cm，则质点做简谐振动的振幅为________cm。

【答案】

16 或 \(\frac{{16}}{3}\)，4 或 \(\frac{{4}}{3}\)

 

18．有一弹簧振子在水平方向上的 B、C 之间做简谐运动，已知 B、C 间的距离为 20 cm，振子在 2 s 内完成了 10 次全振动，若从某时刻振子经过平衡位置时开始计时（t = 0），经过 \(\frac{{1}}{4}\) 周期振子有负向最大位移。

（1）求该振子的振幅和周期；

（2）画出该振子的振动图像（画出一个周期）；

（3）写出该振子的位移随时间变化的关系式。

【答案】

（1）10 cm，0.2 s

（2）如图

（3）x = − 10sin（10πt）

 

19．关于简谐运动，下列说法正确的是（    ）

A．回复力与位移成正比，方向有时与位移相同，有时与位移方向相反

B．加速度与位移成正比，方向永远与位移方向相反

C．速度与位移成反比，方向与位移有时相同、有时相反

D．加速度与回复力成反比，方向永远相同

【答案】

B

 

20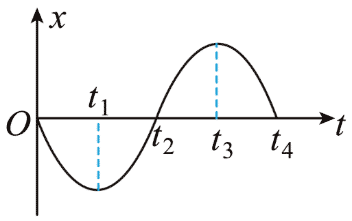．一质点做简谐运动的图像如图所示，下列说法正确的是（    ）

A．0 ~ t₁ 的时间内，质点的位移方向和加速度方向均为负

B．t₁ 到 t₂ 的过程中，质点的速度大小和加速度大小均增大

C．t₂ 到 t₃ 的过程中，质点的位移大小和加速度大小均增大

D．t₃ ~ t₄ 的时间内，质点的位移方向和速度方向均为正

【答案】

C

 

21．如图，弹簧下面挂一质量为 m 的物体，物体在竖直方向上做振幅为 A 的简谐运动，物体振动到最高点时，弹簧正好为原长，则在振动过程中（    ）

A．物体的最大动能应等于 mgA

B．弹簧的弹性势能和物体的动能总和不变

C．弹簧的最大弹性势能等于 2mgA

D．物体在最低点时的弹力大小应小于 2mg

【答案】

C

 

22．对简谐运动的回复力公式 F = − kx 的理解，正确的是（    ）

A．k 只表示弹簧的劲度系数                   B．式中的负号表示回复力总是负值

C．位移 x 是相对平衡位置的位移          D．回复力只随位移变化，不随时间变化

【答案】

C

 

23．简谐运动的平衡位置是指（    ）

A．速度为零的位置                   B．回复力为零的位置

C．加速度为零的位置               D．位移最大的位置

【答案】

B

 

24．做简谐运动的物体连续两次通过同一位置（非最大位移处）时，物理量有变化的是（    ）

A．速度        B．加速度            C．位移        D．动能

【答案】

A

 

25．做简谐运动的物体，当其位移为负时，下列说法正确的是（    ）

A．速度一定为正值，加速度一定为负值

B．速度一定为负值，加速度一定为正值

C．速度不一定为负值，加速度不一定为正值

D．速度不一定为负值，加速度一定为正值

【答案】

D

 

26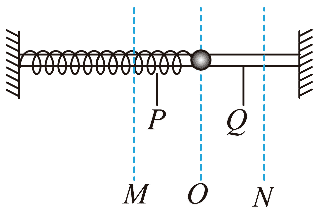．如图，一个弹簧振子在 M、N 之间做简谐运动。P、Q 是关于平衡位置 O 对称的两点，下列说法正确的是（    ）

A．振子在从 M 点向 N 点运动过程中，动能先减小后增大

B．振子在 OP 间与在 OQ 间的运动时间相等

C．振子运动到 P、Q 两点时，位移相同

D．振子在从 M 点向 N 点运动过程中，加速度先增大后减小

【答案】

B

 

27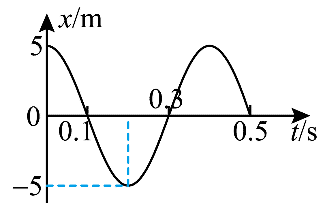．某弹簧振子做简谐运动，其振动图像如图所示，由图可知（    ）

A．在 t = 0 时，振子的动能最小

B．在 t = 0.1 s 时，振子具有最大势能

C．在 t = 0. 25 s 时，振子加速度方向为负方向

D．在 t = 0.5 s 时，振子位移为零，所以振动系统的能量为零

【答案】

A

 

28．一个质点做简谐运动，当它们的加速度逐渐增大时，速度一定在逐渐_________（选填“增大”或“减小”），位移减小时，质点一定朝________（选填“平衡位置”或“两侧”）运动。

【答案】

减小，平衡位置

 

29．一弹簧振子的周期为 1.2 s，当振子开始从平衡位置向右运动，恰经 0.8 s 时，振子向_______（选填“左”或“右”）做加速度变_________（选填“大”或“小”）的_________（选填“加速”或“减速”）运动。

【答案】

左，大，减速

 

30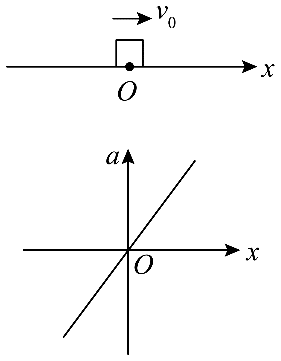．某物体以初速度 v₀ 从原点出发沿 x 轴正方向运动，其加速度 a 随位置 x 的关系如图所示，则该物体的运动__________简谐运动（选填“是”或“不是”），理由是_________________________________。

【答案】

不是，由图像可知加速度方向远离平衡位置，而简谐运动的加速度是指向平衡位置的

 

31．如图，弹簧振子在光滑水平面上以振幅 A 做简谐运动，质量为 M 的滑块上面放一质量为 m 的砝码，砝码随滑块一起做简谐运动，已知弹簧的劲度系数为 k，试求：

（1）使砝码随滑块一起振动的回复力是什么？它跟位移成正比的比例常数 kʹ 等于多少？

（2）当滑块运动到振幅一半位置时，砝码所受的回复力多大？方向如何？

【答案】

（1）使砝码随滑块一起做简谐运动的回复力是滑块对砝码的静摩擦力。

kʹ = \(\frac{m}{{M + m}}\)k

（2）F_回 = \(\frac{{mkA}}{{2(M + m)}}\)，方向指向平衡位置

 

32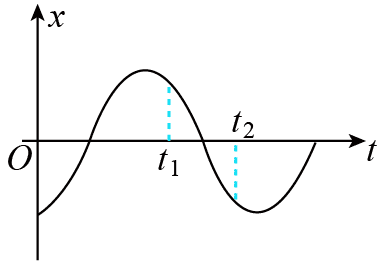．如图所示为某弹簧振子做简谐运动的振动图像，若 t₁、t₂ 时刻振子所处的位置关于平衡位置对称，下列说法正确的是（    ）

A．t₁、t₂ 时刻，振子的速度相同

B．t₁、t₂ 时刻，振子的加速度相同

C．t₁ 至 t₂ 这段时间，振子的速度方向改变

D．t₁ 至 t₂ 这段时间，振子的加速度方向不变

【答案】

A

 

33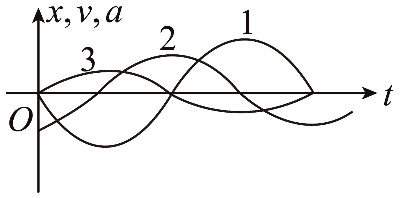．如图，三条曲线分别表示简谐运动中的位移 x、速度 v 和加速度 a，下列说法正确的是（    ）

A．曲线 3、2、1 分别表示 x、v、a 曲线     B．曲线 2、1、3 分别表示 x、v、a 曲线

C．曲线 1、3、2 分别表示 x、v、a 曲线     D．曲线 1、2、3 分别表示 x、v、a 曲线

【答案】

D

 

34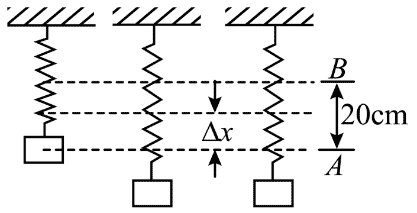．如图，将弹簧振子从平衡位置拉下一段距离 Δx，释放后振子在 A、B 间振动。设 AB = 20 cm，振子由 A 到 B 的时间为 0.1 s，则下列说法正确的是（    ）

A．振子的振幅为 20 cm，周期为 0.2 s

B．振子在 A、B 两处受到的回复力分别为 kΔx + mg 与 kΔx − mg

C．振子在 A、B 两处受到的回复力大小都是 kΔx

D．振子一次全振动通过的路程是 20 cm

【答案】

C

 

35．下列关于简谐运动的说法正确的是（    ）

A．做简谐运动的质点，经过 \(\frac{3}{4}\) 个周期所通过的路程一定等于 3 倍的振幅

B．做简谐运动的质点，离开平衡位置的位移相同时，加速度也相同

C．做简谐运动的质点，在半个周期内，合外力的冲量一定不为零

D．做简谐运动的质点，在半个周期内，合外力做的功一定为零

【答案】

BD

 

36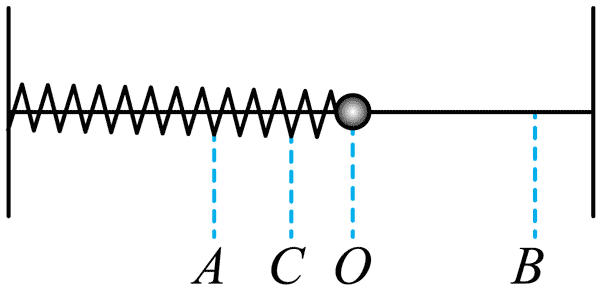．如图，一弹簧振子做简谐运动，取向右为正方向，A、B 两处为最大位移处，O 为平衡位置，C 为 AO 间某一位置。则振子（    ）

A．从 B→O 时，位移是正值，加速度为正值

B．从 O→B 时，位移是正值，速度为正值

C．运动到 C 处时，位移为负值，加速度为正值，速度可能为正值

D．运动至 C 处时，位移为正值，加速度为负值，速度可能是负值

【答案】

BC

 

37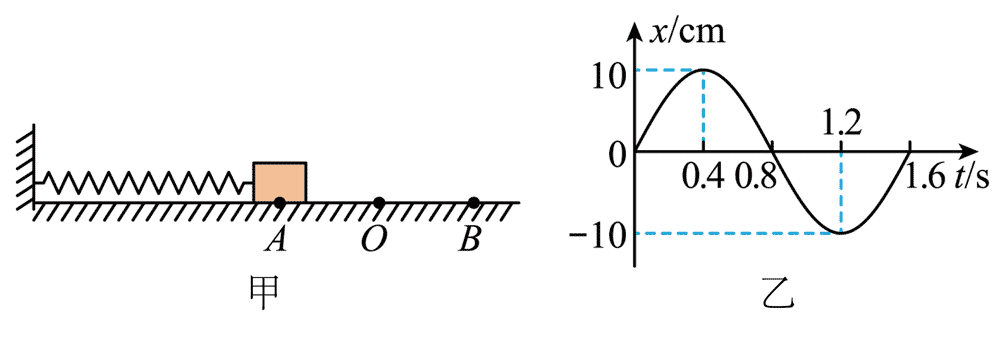．（多选）如图甲，弹簧振子以 O 点为平衡位置，在 A、B 两点之间做简谐运动。取向右为正方向，振动物体的位移 x 随时间 t 的变化如图乙所示，则由图可知（    ）

A．t = 0.2 s 时，振动物体的加速度方向向左

B．t = 0.6 s 时，振动物体的速度方向向右

C．在 t = 0.4 s 到 t = 0.8 s 时间内，振动物体的动能逐渐增大

D．在 t = 0 到 t = 2.4 s 时间内，振动物体通过的路程是 80 cm

【答案】

AC

 

38．一个弹簧振子在水平面内做简谐运动，其表达式为 x = 10sin（10πt + π），该弹簧振子周期 T =__________s。从 t = 0 时开始，经过__________s，弹簧振子第一次具有正向最大加速度。弹簧振子在第一个周期内，从__________s 到__________s 沿正方向运动且弹性势能逐渐增大。

【答案】

0.2，0.05，0.10，0.15

 

39．如图所示为两个弹簧振子 A、B 做简谐运动的振动图像。

（1）求弹簧振子 A 的振幅和周期；

（2）8 ~ 10 s 内，振子 B 的加速度大小如何变化，方向如何？

（3）在 t = 10 s 时，A、B 振子都通过平衡位置，并且它们的速度大小相等、方向相反，从此时起，至少再经过多长的时间，它们再同时通过平衡位置且速度相同；

（4）写出两个弹簧振子的位移与时间的关系式。

【答案】

（1）1 cm，s

（2）加速度逐渐减小，方向指向平衡位置

（3）20 s

（4）x_A = sin（0.15πt +1.5π），x_A = 0.8sin（0.2πt）

 

40．单摆在振动过程中，对摆球的分析正确的是（    ）

A．摆球在最低点的加速度为零

B．合外力方向始终与速度方向垂直

C．摆球在最高点的合外力为零

D．摆球在任何位置的加速度都不等于零

【答案】

D

 

41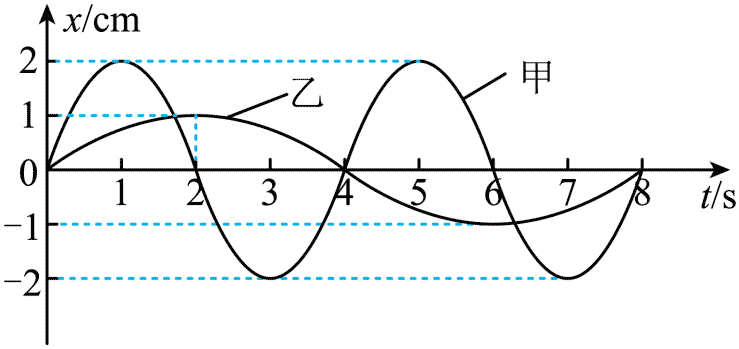．  （多选）甲、乙两个单摆的振动图像如图所示，由图可知（    ）

A．当 t = 2 s 时，甲的摆线拉力为零，乙的速度为零

B．当 t = 4 s 时，甲、乙的速度方向相反

C．甲、乙两个单摆的振幅之比是 4∶1

D．甲、乙两个单摆的摆长之比是 1∶4

【答案】

BD

 

42．如图，几个摆长相同的单摆，它们在不同条件下的周期分别为 T₁、T₂、T₃、T₄，关于周期大小关系的判断，正确的是（    ）

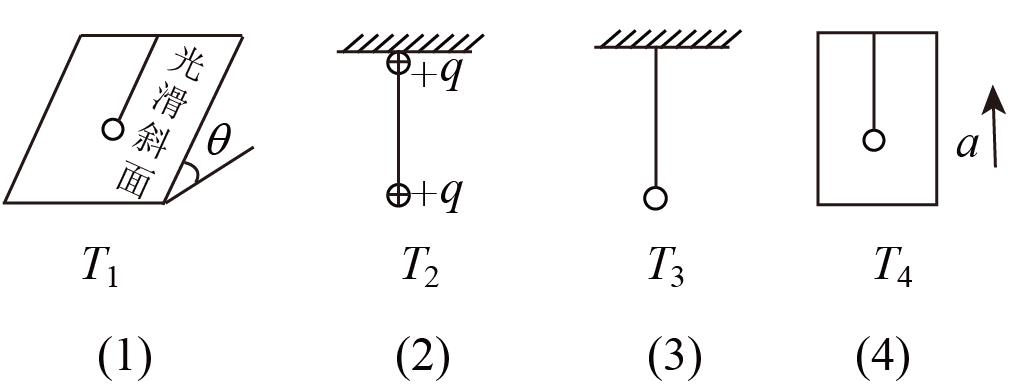
A．T₁ > T₂ > T₃ > T₄               B．T₁ < T₂ < T₃ < T₄

C．T₁ < T₂ = T₃ < T₄               D．T₁ > T₂ = T₃ > T₄

【答案】

D

 

43．关于单摆，下列说法正确的是（    ）

A．物体能被看作单摆的条件是摆动时摆角要小于 5°

B．摆角小于 5° 时振动的频率与振幅无关

C．细线拉力与重力的合力提供回复力

D．摆动到最低点时摆球的合力为零

【答案】

B

 

44．为使单摆的周期变长，可采取的方法是（    ）

A．振幅适当加大        B．将单摆从广州移到北京

C．摆球质量增大        D．摆长适当加长

【答案】

D

 

45．同一地点有甲、乙两个单摆，摆球质量之比 m_甲∶m_乙 = 1∶2，它们都在做简谐运动。甲摆动 4 次时，乙恰好摆动 5 次。可以判断这两个单摆摆长之比 l_甲∶l_乙 为（    ）

A．25∶16            B．16∶25            C．8∶5        D．2∶5

【答案】

A

 

46．如图，用两不可伸长的轻绳悬挂一个小球，两绳长度均为 L、两绳之间的夹角 α 已知，小球的半径为 r，当小球垂直于纸面做简谐运动时，其周期为（    ）

A．2π \(\sqrt {\frac{L}{g}} \)         B．2π \(\sqrt {\frac{{L\cos \frac{\alpha }{2}}}{g}} \)

C．2π \(\sqrt {\frac{{L + r}}{g}} \)           D．2π \(\sqrt {\frac{{L\cos \frac{\alpha }{2} + r}}{g}} \)

【答案】

D

 

47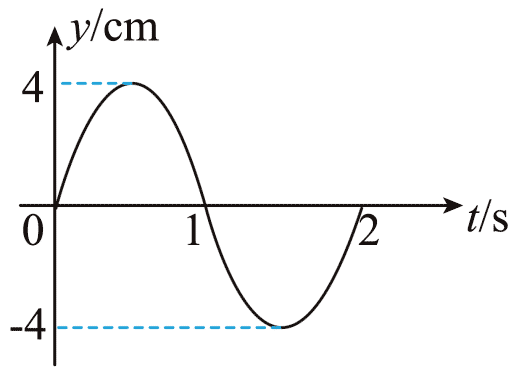．一条较长细线下面挂一个小球就可构成一个单摆。单摆在竖直平面内自由摆动，其做简谐运动的振动图像如图所示。则下列说法正确的是（    ）

A．该单摆的频率为 2 Hz

B．该单摆的摆长大约为 2 m

C．根据图中的数据不能估算出它摆动的最大摆角

D．若将此单摆从山脚移到山顶，单摆的周期将会变大

【答案】

D

 

48．一个单摆的振动周期是 2 s，求下列情况下做简谐运动的单摆周期。

（1）摆长缩短为原来的 \(\frac{1}{4}\)，单摆的周期为_________s；

（2）摆球的质量减为原来的 \(\frac{1}{4}\)，单摆的周期为_________s；

（3）振幅减为原来的 \(\frac{1}{4}\)，单摆的周期为_______。

【答案】

（1）1

（2）2

（3）2

 

49．（1）在上海，为了制作一个周期为 1 s 的单摆，则摆长 l 应取何值？

（2）如果将上一问中制作的单摆运到北京，此单摆在一天内完成的全振动次数是多少？

（3）如果我们认为这个单摆完成一次全振动的时间为“1 s”并用其计时，在北京，这个计时器是偏快还是偏慢？如果一个计时器一天内的偏差超过 1 min，我们就需要每天校准。对于这个单摆计时器（摆钟），是否需要每天校准？

（已知上海的重力加速度 g₁ = 9. 796 4 m/s²，北京的重力加速度 g₂ = 9.801 5 m/s²）

【答案】

（1）l = 0.248 4 m。

（2）约为 86 426次。

（3）这个计时器偏快，一天内的偏差 Δt = 26 s，偏差不足 1 min，故不需要每天校准。

 

50．一单摆做简谐运动，若保持摆长不变，摆球的质量减少为原来的一半，摆球经过平衡位置时的速度增加为原来的 3 倍，则单摆振动的（    ）

A．频率变大，振幅变小            B．频率变小，振幅变大

C．频率不变，振幅变小            D．频率不变，振幅变大

【答案】

D

 

51．内部装满水的空心球用轻绳悬挂在一固定点，使球在竖直面内做小角度摆动，若球的底部是漏水的，则随着水的流失，其摆动周期将（    ）

A．总是变大                      B．总是变小

C．先变小再变大               D．先变大再变小

【答案】

D

 

52．在某一密度均匀的球形星体上，做摆长为 l 的单摆实验。若星体的半径为 R，质量为 M，引力常量为 G，则该单摆的周期为（    ）

A．4πR \(\sqrt {\frac{l}{{GM}}} \)          B．2πR \(\sqrt {\frac{2l}{{GM}}} \)          C．2πR \(\sqrt {\frac{l}{{GM}}} \)          D．πR \(\sqrt {\frac{l}{{GM}}} \)

【答案】

C

 

53．（多选）摆长为 1 m 的单摆做小角度的摆动，振动过程的最大位移为 6 cm，不计空气阻力，重力加速度 g 取 π² m/s²，从摆球向右通过最低点开始计时，则从 t = 1 s 到 t = 2 s 的过程中（    ）

A．摆球的重力势能先减小后增大            B．摆球的动能先减小后增大

C．摆球振动的回复力先减小后增大        D．摆球的切向加速度先增大后减小

【答案】

BD

 

54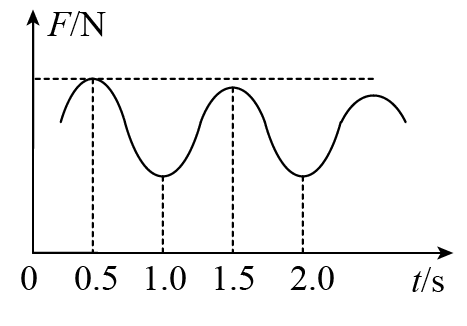．（多选）将某单摆的摆线上端系在一个力传感器上，单摆摆动过程中，摆线张力随时间的变化规律如图所示。已知单摆的摆角小于 5°，重力加速度 g = π² m/s²，则下列说法正确的是（    ）

A．单摆的周期为 1 s

B．单摆的摆长为 1 m

C．当 t = 0.5 s 时，摆球正经过最低点

D．摆球运动过程中周期越来越小

【答案】

BC

 

55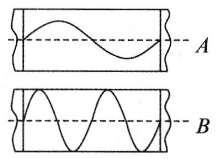．用甲、乙两个沙摆演示简谐运动的振动图像，如图所示为两个沙摆在各自木板上形成的曲线，若 A、B 两板拉动的速度之比 v_A∶v_B = 1∶2，则两摆摆动的周期之比 T_A∶T_B = _________，摆长之比 l_A∶l_B  = ______。

【答案】

4∶1，16∶1

 

56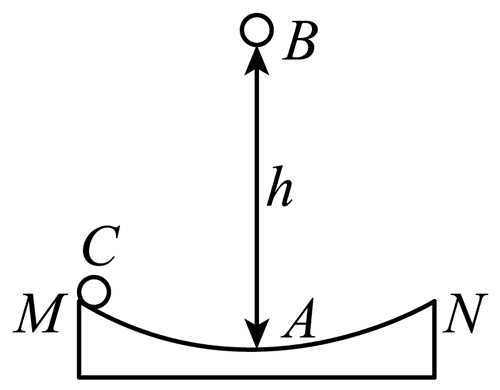．如图，光滑的弧形槽的半径为 R（R 远大于弧长 MN），A 为弧形槽的最低点。小球 B 放在 A 点正上方，离A点的高度为 h，小球 C 放在 M 点，同时释放两球，使两球正好在 A 点相碰，则从建立模型的角度分析，小球 C 的运动可视为______模型，h 应为______。

【答案】

单摆，\(\frac{1}{8}\)π²（2n + 1）²R（n = 0，1，2，…）

 

57．摆钟是一种利用摆的等时性制成的计时装置，它具有下列特性：钟摆的振动可以等效成是单摆的简谐运动，摆钟的指示时间与摆钟的振动次数成正比。现有一座摆钟，摆长为 1 m，一昼夜快 10 min，要使它走时正确，应该将摆长调到多长？（结果精确到 0.001 m）

【答案】

应将摆长调到1.014 m。

 

58．某同学利用单摆测量当地的重力加速度。

（1）实验室有多种足够长的细线可用来制作单摆，由于材质不同，这些线的质量、弹性各不相同，为更好地完成实验，该同学应选择怎样的摆线？请分析说明：___________。

（2）该同学经测量得到 6 组摆长 l 和对应的周期 T，画出 l – T² 图像，然后在图像上选取 A、B 两个点，如图所示。则当地重力加速度的表达式 g = __________。处理完数据后，该同学发现在计算摆长时用的是摆线长度而未计入小球的半径，这样__________（选填“影响”或“不影响”）重力加速度的计算。

（3）该同学在实验时有下列操作：

A．摆线偏离竖直方向的最大摆角小于 5°

B．当小球通过平衡位置时开始计时

C．摆球未在竖直面内摆动，摆成了圆锥摆

D．计时开始后测得摆球第 n 次经过平衡位置所用的时间为 t，记录单摆的周期 T = \(\frac{{2t}}{n}\)

以上操作中你认为__________存在问题，试分析说明该操作对测量结果有何影响：_____________________。

【答案】

（1）为了保证在实验过程中摆长不发生变化，摆线应选无弹性的材质

（2）\(\frac{{4{\pi ^2}({l_B} - {l_A})}}{{T_B^2 - T_A^2}}\)，不影响

（3）C，测量结果偏小

 

59．“用单摆测量重力加速度的大小”的实验装置如图所示。

（1）（多选）组装单摆时，应在下列器材中选用（    ）

A．长度为 1 m 左右的细线

B．长度为 30 cm 左右的橡皮绳

C．直径为 1.8 cm 的塑料球

D．直径为 1.8 cm 的铁球

（2）单摆完成 n 次全振动所用的时间 t，则单摆的周期 T = __________；

（3）测出悬点 O 到小球球心的距离（摆长） l，则当地的重力加速度 g = __________表示）。

【答案】

（1）AD

（2）\(\frac{t}{n}\)

（3）\(\frac{{4{\pi ^2}{n^2}l}}{{{t^2}}}\)

 

60．某位同学用下列器材来测量当地的重力加速度：他选择一个半径 r 较大的表面光滑的凹面镜、一个小砝码和一个停表。具体实验步骤如下：

① 将凹面镜水平固定放置，将小砝码从凹面镜边缘静止释放，如图所示。

② 当小砝码滑至凹面镜最低点时按停表计时，同时数作“1”，接着一直数到小砝码第 60 次通过最低点时，按停表停止计时。读出这段记录的时间 t，算出小砝码振动的周期 T = \(\frac{t}{60}\)。

③ 利用所求得的 T 代入到 g = \(\frac{{4{\pi ^2}r}}{{{T^2}}}\) 中即测得重力加速度。

请你分析他的实验方法是否存在不完善或错误？如果有，写出该步骤的序号并加以说明或纠正。

【答案】

① 不完善，在边缘释放有可能最大摆角已超过 5°；

② 错误，应数作“0”或改周期 T = \(\frac{t}{29.5}\)；

③ 不完善，应多测几次取平均值。

 

61．某同学利用实验来验证单摆周期 T 与摆长 l 的关系。

（1）（多选）为了完成实验并使实验结果尽可能精确，除了铁架台外，在下列器材中还应选用（    ）

A．游标卡尺               B．米尺               C．秒表        D．天平

E．测力计            F．长度不同的细线     G．中心有小孔的钢球

（2）（多选）为了尽量准确获得 T² – l 图像，在下列测量步骤中必须进行的是（    ）

A．测量小球的质量                   B．测量悬点到小球上端的距离

C．测量小球的直径                   D．测量细线中的拉力

E．测量单摆小角度摆动 50 个周期所用的时间

F．改变摆长，进行重复测量

（3）（单选）某同学获得的 T² – l 图像如图中实线所示，T² – l 理论关系如图中虚线所示，造成这个结果可能的原因是（    ）

A．计算摆长时，取从悬点到小球上端的长度

B．计算摆长时，取从悬点到小球下端的长度

C．用不同的摆长进行实验时摆角选取不同

D．选用的摆球质量偏大

【答案】

（1）ABCFG

（2）BCEF

（3）B

 

62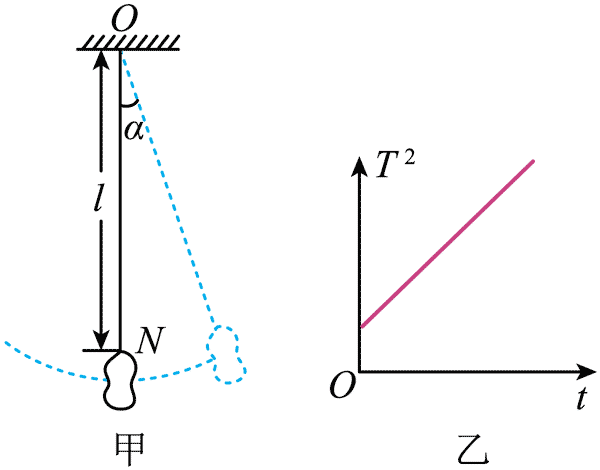．某同学在家做“用单摆测量重力加速度的大小”的实验，他使用一块外形不规则的小石块代替摆球，如图甲所示。

（1）（多选）下列实验操作中，正确的是（    ）

A．摆线要选择不可伸缩、尽量长一些的细线；

B．用刻度尺测量 ON 间细线的长度 l，l 就是单摆摆动的摆长；

C．将石块拉开一个大约 α = 5° 的小角度，然后由静止释放；

D．从石块摆至最低点开始计时，测出30次全振动的总时间 t，由 T = \(\frac{t}{30}\) 计算出周期；

（2）这位同学用 ON 的长 l 为摆长，利用公式求出的重力加速度的测量值比真实值_________（选填“偏大”或“偏小”）；

（3）该同学利用测出的多组摆长 l 和周期 T 的数值，作出 T² – l 图像如图乙所示，若图像的斜率为 k，则重力加速度的表达式 g = __________。

【答案】

（1）ACD

（2）偏小

（3）\(\frac{{4{\pi ^2}}}{k}\)

 

63．“用单摆测量重力加速度的大小”的实验装置如图所示。

（1）实验前根据单摆周期公式推导出重力加速度的表达式，四位同学对表达式有不同的观点：

同学甲认为，T 一定时，g 与 l 成正比；

同学乙认为，l 一定时，g 与 T² 成正比；

同学丙认为，l 变化时，T² 是不变的；

同学丁认为，l 变化时，l 与 T² 的比值是定值。

其中观点正确的是同学_______________。

（2）实验时摆线与悬点连接处用铁架夹住摆线，用米尺测得摆线长度，用游标卡尺和秒表分别测得摆球直径和 50 次全振动时间。表格是某次记录的一组数据，请填表。

次数	摆线长度/cm	摆球直径/cm	50 次全振动时间/s	摆长 l /cm	重力加速度 g /（m·s−2）
1	97.0	2.0	100.0

【答案】

（1）丁

（2）98.0，9.66

 

64．在“用单摆测量重力加速度的大小”的实验中。

（1）（多选）下列做法正确的是

A．选择密度较小的摆球

B．用夹子夹牢摆线，再用铁架台的铁夹将夹子夹紧，确保摆长不变

C．把单摆从平衡位置拉开 5° 的摆角，并在释放摆球的同时开始计时

D．保证摆球在同一竖直平面内摆动

（2）测摆长时，若正确测出悬线长 l = 96 cm 和摆球直径 d = 2 cm，则摆长为________m。

（3）测周期时，当摆球经过_________位置时，开始计时并计数 1 次，测出经过该位置 100 次用时为 98 s，则周期为_________s（保留小数点后两位）。

（4）多次改变摆长，使单摆做小角度摆动，测量摆长 l 及相应的周期 T。此后，分别取 l 和 T 的对数，所得到的 lgT – lgl 图像为_____________（选填“直线”“对数曲线”或“指数曲线”）；读得图像与纵轴交点的纵坐标为 c，由此得到该地重力加速度 g = _________。

【答案】

（1）BD

（2）0.97

（3）平衡（或最低点），1.98

（4）直线，\(\frac{{4{\pi ^2}}}{{{{10}^{2c}}}}\)

 

65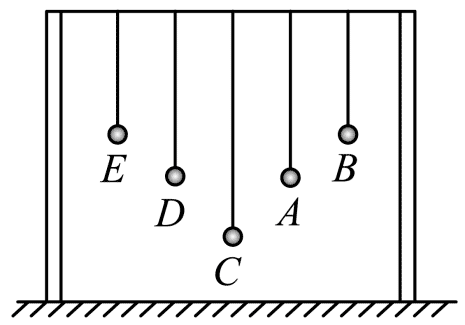．如图，薄金属条上挂有 5 个相同的小球 A、B、C、D、E，细线质量可忽略，线长远大于球半径，A、D 两球的线长相等，使 A 小角度垂直于纸面摆动，其余各球随之开始摆动，稳定后（    ）

A．C振动的周期最长

B．B 振动的周期最短

C．B、C、D、E 均为受迫振动

D．C 的振幅最大

【答案】

C

 

66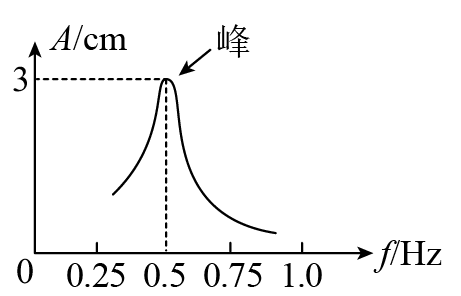．如图所示为一个单摆做受迫振动时振幅 A 与驱动力的频率 f 的关系，下列说法正确的是（    ）

A．该单摆摆长约为 6 cm

B．发生共振时单摆的周期为 1 s

C．单摆实际摆动的频率可能大于驱动力的频率

D．若增大摆长，则曲线的“峰”将向左移动

【答案】

D

 

67．下列各种振动中，不是受迫振动的是（    ）

A．敲击后的锣面振动                      B．缝纫机针的振动

C．人挑担子时，担子上下振动        D．蜻蜓、蝴蝶翅膀的振动

【答案】

A

 

68．关于受迫振动和共振，下列说法正确的是（    ）

A．做受迫振动物体的机械能守恒

B．火车过桥时限制速度是为了防止火车发生共振

C．声音可振碎玻璃杯是因为玻璃杯发生了共振

D．物体受迫振动达到稳定后，其振动频率由驱动力频率和固有频率共同决定

【答案】

C

 

69．受迫振动在稳定状态时（    ）

A．一定做简谐运动                          B．不可能是简谐运动

C．一定按驱动力的频率振动            D．一定发生共振

【答案】

C

 

70．超声波洁牙机利用超声波激励工作头产生高频振动，使牙结石因振动而松脱。下列说法正确的是（    ）

A．工作头的振动频率小于超声波的频率

B．工作头的振动频率与牙结石固有频率接近时，牙结石更容易脱落

C．工作头的振动频率越大，洁牙效果越好

D．工作头停止振动，牙结石的固有频率逐渐减小

【答案】

B

 

71．有甲、乙两个弹簧振子，甲的固有频率为 f，乙的固有频率为 9f，若它们均在频率为 8f 的驱动力作用下受迫振动，则（    ）

A．甲的振幅较大，振动频率为 f

B．乙的振幅较大，振动频率为 9f

C．甲的振幅较大，振动频率为 9f

D．乙的振幅较大，振动频率为 8f

【答案】

D

 

72．一物体做受迫振动，最初驱动力的频率小于该物体的固有频率，则在驱动力的频率逐渐增大到一定数值的过程中，该物体的振幅可能（    ）

A．保持不变                             B．逐渐减小

C．先逐渐增大，后逐渐减小     D．先逐渐减小，后逐渐增大

【答案】

C

 

73．共振是一种受迫振动，共振时，驱动力的频率等于做受迫振动物体的_________，物体的振幅_________。微波炉就是利用____________________________工作的，它的工作频率与_________频率相同。

【答案】

固有频率，最大，共振，水分子或食物分子的共振，固有

 

74．大海中航行的轮船，受到大风大浪冲击时，为了防止倾覆，应当改变航行方向和_________，使风浪冲击力的频率远离轮船摇摆的_________。

【答案】

速度，固有频率

 

75．匀速运行的火车的车厢里用细线吊着一个小球形成一个单摆，细线长为 l，则该单摆的固有周期 T = _________。在铁轨接合处火车会产生振动，从而使球摆动。如果每根铁轨长为 L，则当火车的速度 v = _________时，球摆动的振幅最大。（已知重力加速度为 g）

【答案】

2π\(\sqrt {\frac{l}{g}} \)，\(\frac{L}{{2\pi }}\sqrt {\frac{g}{l}} \)

 

76．如图所示为研究受迫振动的实验装置，弹簧振子悬挂在 O 点，如果转动摇柄，曲轴可以带动弹簧振子上下振动。问：

（1）开始时不转动摇柄，而用手往下拉振子，然后放手让振子上下振动，测得振子在 10 s内完成 20 次全振动，此时振子做什么振动？其固有周期和固有频率各是多少？

（2）在振子正常振动过程中，以转速 4 r/s 匀速转动摇柄，振子的振动稳定后，振子做什么运动？其周期是多少？

（3）若要振子振动的振幅最大，摇柄的转速应为多大？为什么？

【答案】

（1）简谐运动，0.5 s，2 Hz

（2）受迫振动，0.25 s

（3）2 r/s。

 

77．一洗衣机正常工作时非常平稳，当切断电源后，发现洗衣机先是振动越来越强烈，然后振动再逐渐减弱，对这一现象，下列说法正确的是（    ）

A．正常工作时，洗衣机波轮的运转频率比洗衣机的固有频率大

B．正常工作时，洗衣机波轮的运转频率比洗衣机的固有频率小

C．正常工作时，洗衣机波轮的运转频率等于洗衣机的固有频率

D．只有当洗衣机振动最剧烈时，洗衣机做受迫振动

【答案】

A

 

78．蜘蛛会根据丝网的振动情况感知是否有昆虫“落网”，若丝网的固有频率为 200 Hz，下列说法正确的（    ）

A．“落网”昆虫翅膀振动的频率越大，丝冈的振幅越大

B．当“落网”昆虫翅膀振动的频率低于 200 Hz 时，丝网不振动

C．当“落网”昆虫翅膀振动的频率等于 200 Hz 时，丝网的振幅最大

D．昆虫“落网”时，丝网振动的频率由丝网的固有频率决定

【答案】

C

 

79．将固有频率分别为 f₁、f₂ 的两振子固定在同一振台上，打开振台后逐渐调大振台的驱动力频率。已知 f₁ < f₂，关于两振子受迫振动的振幅 A₁、A₂，则（    ）

A．A₁、A₂ 不可能同时增大

B．A₁ 增大的同时 A₂ 不可能减小

C．A₁、A₂ 不可能同时减小

D．A₁ 减小的同时 A₂ 不可能增大

【答案】

B

 

80．如图甲，在一条紧绷的绳子上挂着 a、b、c、d 四个摆。当以摆振动的时候，其余各摆在 a 摆的驱动下也逐步振动起来，不计空气阻力，达到稳定时，b 摆的振动图像如图乙所示，下列说法正确的是（    ）

A．稳定时 b 摆的振幅最大                    B．稳定时 d 摆的周期最小

C．由图乙可以估算出 b 摆的摆长          D．由图乙可以估算出 c 摆的摆长

【答案】

D

 

81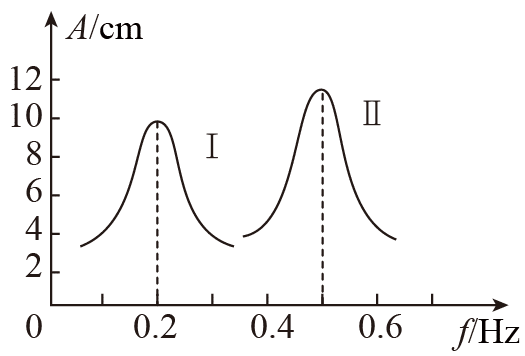．如图所示为摆长为 1 m 的单摆分别在地球表面和某星球表面做受迫振动的共振曲线，已知地球表面重力加速度大小为 10 m/s²。下列说法正确的是（    ）

A．图线 Ⅰ 是某星球上的单摆共振曲线，图线 Ⅱ 是地球上的单摆共振曲线

B．图线 Ⅰ 是地球上的单摆共振曲线，图 Ⅱ 是某星球上的单摆共振曲线

C．将一摆钟从地球移到该星球上，摆钟会变快

D．该星球表面重力加速度约为 62.5 m/s²

【答案】

A

 

82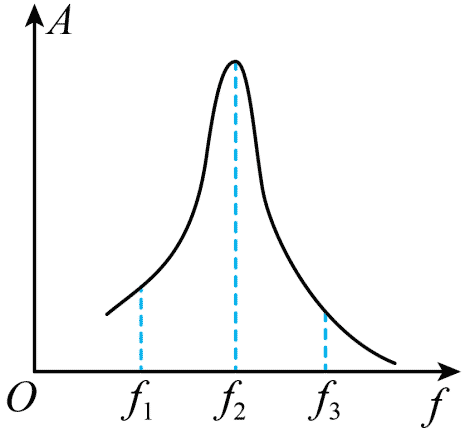．（多选）一弹簧振子做受迫振动时的振幅与驱动力频率的关系如图所示。下列说法正确的是（    ）

A．假如让振子自由振动，它的频率为 f₂

B．驱动力的频率为 f₂ 时，振子处于共振状态

C．驱动力的频率为 f₃ 时，振子的振动频率为 f₃

D．振子做自由振动时，频率可能为 f₁、f₂ 和 f₃

【答案】

ABC

 

83．（多选）据《天中记》一书记载，晋初（公元 3 世纪）时，皇宫附近有户人家挂着的铜盘每天早晚轻轻自鸣两次，人们十分惊恐。有学者判断这是铜盘与皇宫早晚的钟声共鸣所致。后来把铜盘磨薄一些，它就不再自鸣了。关于这个现象，下列说法正确的是（    ）

A．共鸣是一种共振

B．铜盘共鸣时的振动频率等于皇宫钟声的频率

C．把铜盘磨薄改变了驱动力的频率

D．把铜盘磨薄使铜盘的固有频率远离驱动力的频率

【答案】

ABD

 

84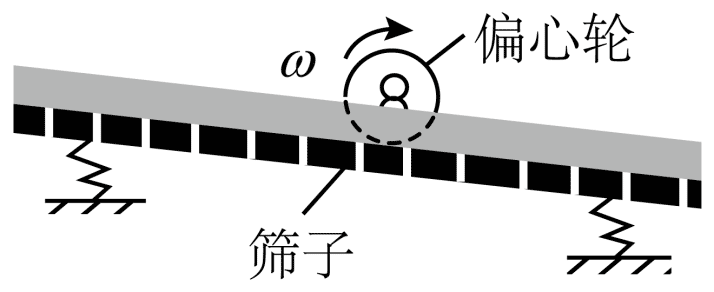．（多选）将一个铁筛四角用四根弹簧支起，筛子上装一个电动偏心轮，它每转动一周给筛子提供一次驱动力。已知增大电动偏心轮的输入电压，可提高转速；增大筛子质量，可增大筛子的固有周期。已知筛子自由振动时完成 10 次全振动用 15 s，电动偏心轮转速为 36 r/min，要使筛子振动的振幅最大，可采用的办法是（    ）

A．提高电动偏心轮的输入电压               B．降低电动偏心轮的输入电压

C．增大筛子的质量                                 D．减小筛子的质量

【答案】

AC

 

85．减震器，是为加速车架与车身振动的衰减，以改善汽车的行驶舒适性的汽配元件，在大多数汽车的悬架系统内部都装有减震器。汽车的重力一般作用于固定在轴承上的若干弹簧上，弹簧套在减震器上，丙者同时起到改善作用。为了研究方便，我们把两者简化成一个等效劲度系数 k = 1.5×10⁵ N/m 的“弹簧”，汽车开始运动时，在振幅较小的情况下，其振动的频率满足 f = \(\frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)（l 为弹簧的压缩长度），若人体可以看成一个弹性体，其固有频率约为 2 Hz，已知汽车的质量为 600 kg，每个人的质量为 70 kg，g 取 10 m/s²。求：

（1）汽车的振动频率与人体固有频率相等时 l 的大小；

（2）这辆车乘坐几个人时，人感觉最颠簸。

【答案】

（1）0.063 m

（2）5 个

 

86．关于简谐运动的特点，下列说法正确的是（    ）

A．回复力跟位移成正比且方向相反          B．回复力与时间成正比

C．速度跟位移成正比且方向相反              D．速度与时间成正比

【答案】

A

 

87．物体做简谐运动时，下列判断正确的（    ）

A．在平衡位置加速度最大                  B．在平衡位置速度最大

C．在运动路径两端速度最大              D．在运动路径两端加速度最小

【答案】

B

 

88．光滑水平面内的弹簧振子做简谐运动，经过半个周期，振子的（    ）

A．动量一定不变          B．速度一定不变          C．加速度一定不变              D．动能一定不变

【答案】

D

 

89．弹簧振子的周期为 2 s，从振子通过平衡位置向右运动起，经过 1.8 s 时，其运动情况是（    ）

A．向右减速          B．向右加速          C．向左减速          D．向左加速

【答案】

B

 

90．如图，表面光滑的固定圆弧轨道，最低点为 P，弧长远小于半径 R，现将可视为质点的两个小球分别从 A、B 点同时由静止释放，AP 大于 BP，则（    ）

A．两球在 P 点相遇                    B．两球在 P 点右侧相遇

C．两球在 P 点左侧相遇            D．以上情况均有可能

【答案】

A

 

91．如图，振子在 a、b 间做简谐运动，O 为平衡位置，设向右为正方向，从某一时刻开始（t = 0）经过 \(\frac{1}{2}\) 周期，振子具有负方向最大加速度，下列能正确反映振子振动情况的是（    ）

【答案】

B

 

92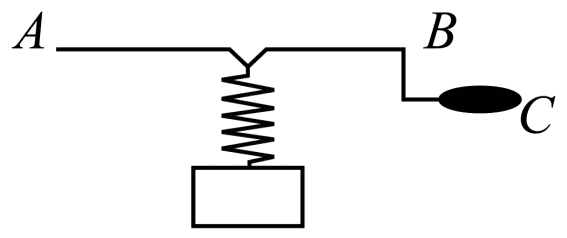．如图所示的装置中，在曲轴 AB 上悬挂一个弹簧振子，若不转动把手 C，让其上下振动，周期为 T₁，若使把手以周期 T₂（T₂ > T₁）匀速转动，当运动都稳定后，则（    ）

A．弹簧振子的振动周期为 T₁

B．弹簧振子的振动周期为 \(\frac{{{T_1} + {T_2}}}{2}\)

C．把手转速减小，可使弹簧振子的振幅增大

D．把手转速增大，可使弹簧振子的振幅增大

【答案】

D

 

93．一个单摆由甲地（重力加速度为 g_甲）移到乙地（重力加速度为 g_乙）后，发现走时变快了，其变快的原因及调整的方法是（    ）

A．g_甲 > g_乙，将摆长缩短          B．g_甲 < g_乙，将摆长放长

C．g_甲 < g_乙，将摆长缩短          D．g_甲 > g_乙，将摆长放长

【答案】

B

 

94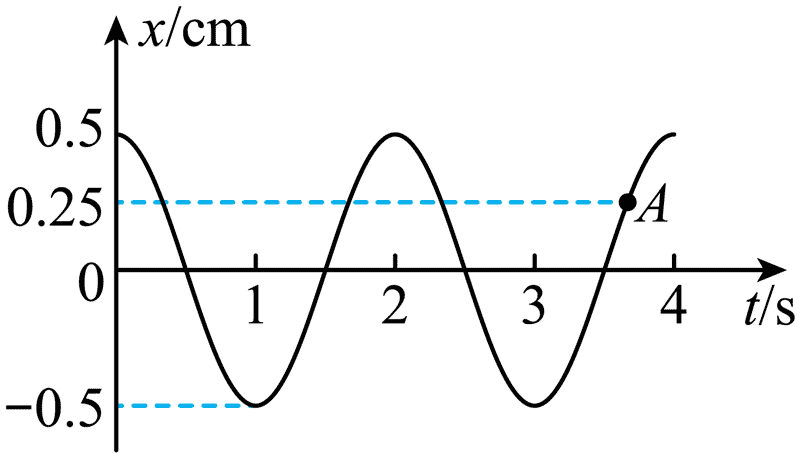．如图所示为水平弹簧振子做简谐运动的振动图像。已知弹簧的劲度系数为 10 N/cm，下列说法正确的是（    ）

A．图中 A 点，振子所受的回复力大小为 2.5 N

B，图中 A 点，振子的速度方向指向 x 轴的负方向

C．弹簧振子的振幅等于 1 cm

D．4 s 内，振子做了 4 次全振动

【答案】

A

 

95．甲、乙两位同学在同一实验室做沙摆实验，以相同速度拉动纸板，在相同长度的纸板上得到的痕迹图像如图所示，下列说法不正确的是（    ）

  

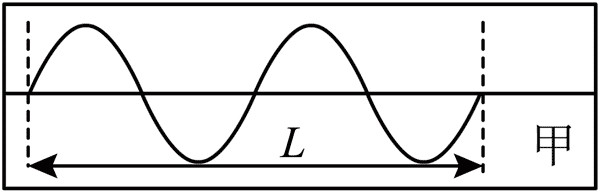
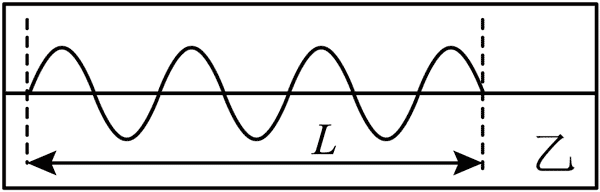
A．沙摆质量的变化对周期的影响较小，可以忽略不计

B．甲、乙两个沙摆的周期之比为 7∶4

C．甲、乙两个沙摆的摆长为 16∶49

D．在误差范围内，甲、乙两同学测得的重力加速度的数值相同

【答案】

C

 

96．做简谐运动的物体，当它每次经过同一位置时，速度_______不同，加速度_______相同。（均选填“可能”或“一定”）

【答案】

可能，一定

 

97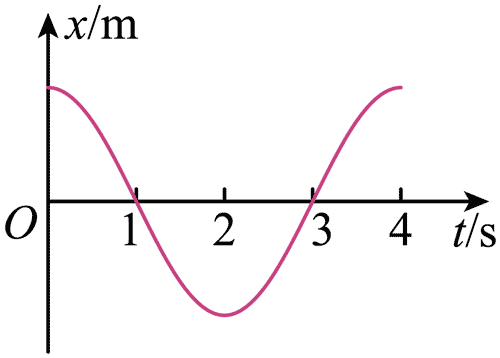．从图中给出的 0 ~ 4 s 内的振动图像可知，振子在_______s 末正方向速度最大，在_______s 末正方向加速度最大，在_______时间范围内振子向正方向振动。

【答案】

3，2，2 ~ 4 s

 

98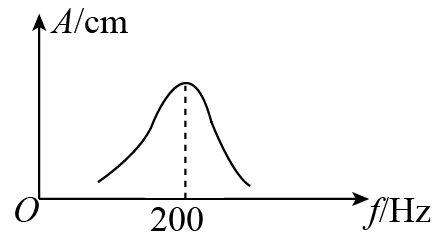．如图所示为某物体做受迫振动时的共振曲线，则该物体振动的固有频率为_______Hz，在驱动力的频率由 150 Hz 增大到 250 Hz 的过程中，物体振动的振幅变化情况是_______。

【答案】

200，先增大后减小

 

99．单摆做简谐运动的周期与摆球的质量_______（选填“有关”或“无关”）。有一劲度系数为 k 的轻质弹簧竖直悬挂，下端系上质量为 m 的物块，将物块向下拉离平衡位置后松开，物块上下做简谐运动，其振动周期恰好等于以物块平衡时弹簧的伸长量为摆长的单摆的周期，则物块做简谐运动的周期为_______。

【答案】

无关，2π\(\sqrt {\frac{m}{k}} \)

 

100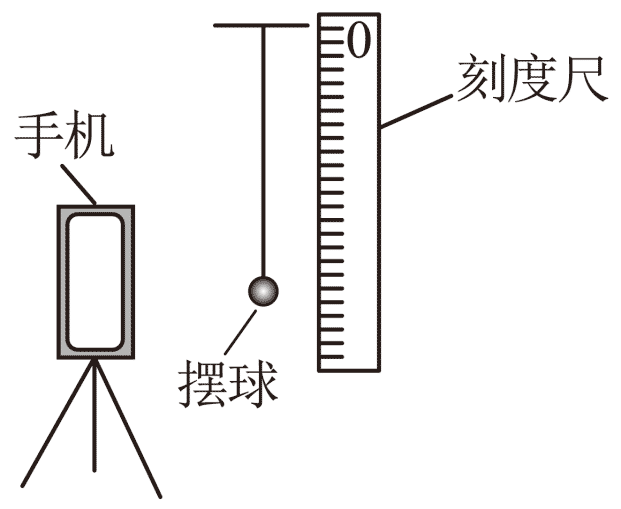．某同学在家里做“用单摆测量重力加速度的大小”的实验，用手机拍摄单摆振动的视频，得到分帧图片，根据图片上显示的位置和时刻，来测当地的重力加速度，实验装置如图所示。

（1）家中有乒乓球、小塑料球和带孔小木球、带孔小钢球，其中最适合做摆球的物体是_____________；

（2）下列主要操作步骤的正确顺序是____________________（选填序号）；

① 把刻度尺竖直固定在墙上；

② 打开手机摄像功能，开始摄像；

③ 手机固定在三脚架上，调整好手机镜头的位置；

④ 把小球拉开一定的小角度，静止释放小球，使其在竖直面内摆动；

⑤ 把小球用长约 1 m 的细线悬挂起来，使其悬点和刻度尺的零刻度对齐；

⑥ 停止摄像，选择合适的分帧图片进行分祈。

（3）从视频中截取小球第 1 次和第 41 次经过最低点时的两帧图片，图片中小球所在位置和时刻如图所示，可以估测单摆的摆长约为________m，单摆的周期为_______s，粗略测得的重力加速度大小为___________m/s²。

【答案】

（1）带孔小钢球

（2）①⑤③②④⑥

（3）0.95，1.95，9.85

 

101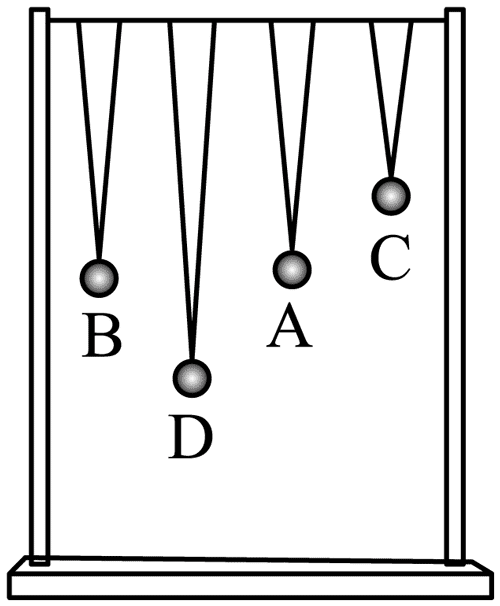．如图，在紧绷的绳子上挂 A、B、C、D 四个摆，其中 A、B 摆长相同。将摆 A 垂直于纸面拉离平衡位置一定距离后释放，摆 A 开始摆动，并通过绳子给摆 B、C、D 施加驱动力，使 B、C、D 做受迫振动，忽略其他能量损耗。

（1）比较四个摆的周期大小，并简要说明理由。

（2）B、C、D 三个摆中哪一个的振幅最大？为什么？

（3）分析摆 A 摆动过程中机械能是否守恒，并简要说明理由。

【答案】

（1）四个摆的周期相同，因为 B、C、D 做受迫振动其振动的频率由驱动力的频率决定，与驱动力的频率相同，即 B、C、D 做受迫振动的周期与 A 的固有周期相同。

（2）受迫振动中，当固有频率等于驱动力频率时，出现共振现象，振幅达到最大，根据固有周期与摆长的关系为 T = 2π\(\sqrt {\frac{l}{g}} \)，f = \(\frac{1}{T}\)，所以 A、B 摆长相同，则固有周期、固有频率相同，可知 B 发生共振，振幅最大。

（3）摆 A 开始摆动，并通过绳子给摆 B、C、D 施加驱动力，使 B、C、D 做受迫振动，忽略其他能量损耗，由能量转化和守恒规律可知，摆 A 的机械能转化为整个系统的机械能，则摆 A 摆动过程中机械能不守恒。

 

102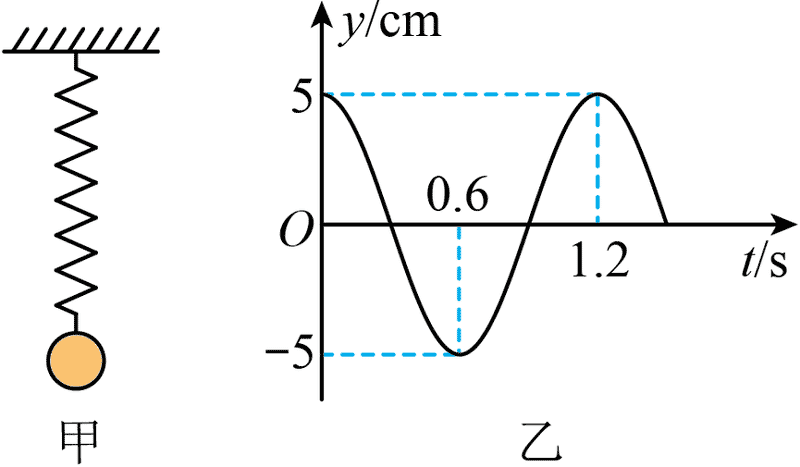．如图甲，轻质弹簧上端固定，下端系一质量 m = 0.2 kg 的小球，小球静止时弹簧伸长量为 8 cm。现使小球在竖直方向上做简谐运动，从小球在最高点释放时开始计时，小球相对平衡位置的位移随时间 t 变化的规律如图乙所示，重力加速度 g 取 10 m/s²。

（1）写出小球相对平衡位置的位移随时间变化的关系式；

（2）求小球在 0 ~ 13 s 内运动的总路程和 13 s 时刻的位置；

（3）求小球运动到最高点时的加速度大小。

【答案】

（1）y = 5cos（\(\frac{{5\pi }}{3}\)t）

（2）y = 2.5 cm，总路程 s = 217.5 cm。

（3）a = 6.25 m/s²

 

103．下列不属于理想模型的是（    ）

A．质点          B．元电荷              C．弹簧振子          D．单摆

【答案】

B

 

104．在竖直方向上做简谐运动的弹簧振子，当振子的速度相等时，下列物理量一定相同的是（    ）

A．弹性势能          B．位移          C．势能          D．加速度

【答案】

C

 

105．关于简谐运动，下列说法正确的是（    ）

A．物体通过平衡位置时，合外力一定为零

B．振子做减速运动时，加速度在减小

C．振子向平衡位置运动时，加速度方向与速度方向相反

D．振子远离平衡位置运动时，加速度方向与速度方向相反

【答案】

D

 

106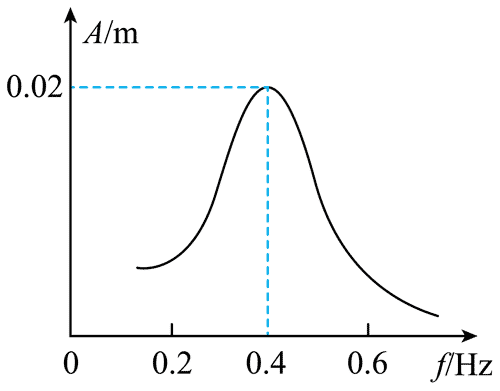．一弹簧振子在驱动力的作用下做受迫振动，其振幅大小与驱动力的频率之间的关系如图所示，下列说法正确的是（    ）

A．弹簧振子的固有频率为 0.02 Hz

B．弹簧振子的固有周期为 50 s

C．弹簧振子做受迫振动时的周期与其固有周期有关

D．弹簧振子共振时具有的能量最大

【答案】

D

 

107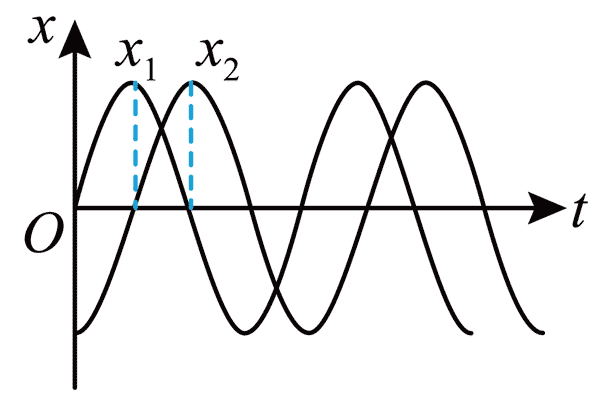．两个同周期的简谐运动的振动图像如图所示，则 x₁ 的相位比 x₂ 的相位（    ）

A．落后 \(\frac{\pi }{2}\)             B．超前 \(\frac{\pi }{2}\)             C．落后 π               D．超前 π

【答案】

B

 

108．汽车在凹凸不平的道路上前进，车厢上下振动，若在某段时间内车厢的振动可看作简谐运动。当车厢振动到哪个位置时，车厢内的人感到车座对该人的支持力最小（    ）

A．振动到最低点时              B．向上振动到经过平衡位置时

C．振动到最高点时              D．向下振动到经过平衡位置时

【答案】

C

 

109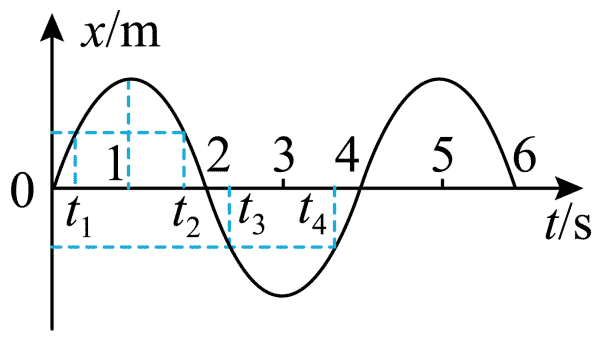．弹簧振子做简谐运动的振动图像如图所示，则（    ）

A．t = 0 时，质点的位移为零，速度为零，加速度为零

B．t = l s 时，质点的位移最大，速度最大，加速度最大

C．t₁ 和 t₂ 时刻振子具有相同的速度

D．t₃ 和 t₄ 时刻振子具有相同的加速度

【答案】

D

 

110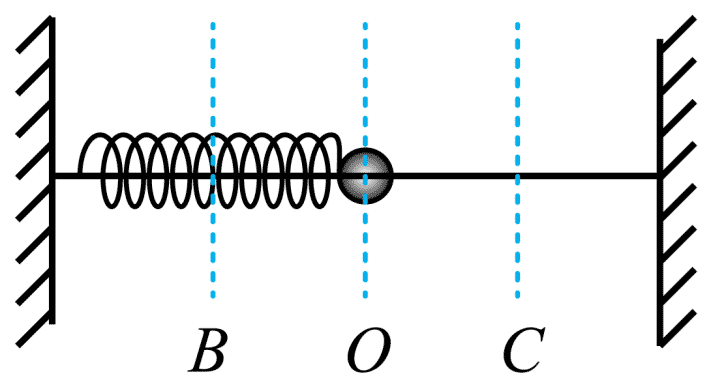．如图，弹簧振子在 B、C 两点间做简谐运动，O 点为平衡位置，B、C 为两侧的最大位置，若振子振幅为 A，由 B 运动到 C 的时间为 2 s，则（    ）

A．从 O 点再次回到 O 点为一次全振动

B．振子经过 4 s，振子通过的路程为 4A

C．振子从 B 到 C 的平均速度为 0.5A m/s

D．振子经过的路程为 A 时所用的时间一定为 1 s

【答案】

B

 

111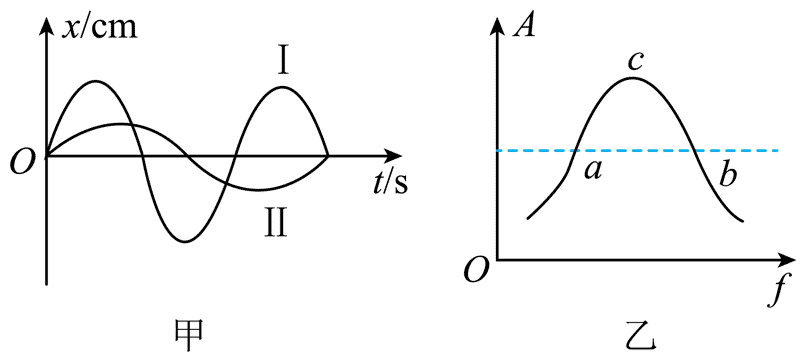．某简谐振子自由振动时的振动图像如图甲中的曲线 Ⅰ 所示，而在某驱动力作用下做受迫振动时，稳定后的振动图像如图甲申的曲线 Ⅱ 所示，那么，此受迫振动对应的状态可能是图乙中共振曲线的（    ）

A．a 点          B．b 点          C．c 点           D．都有可能

【答案】

A

 

112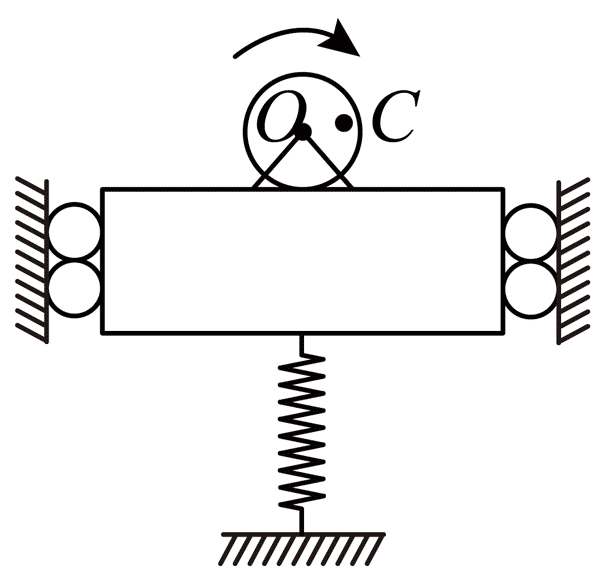．如图，一个偏心轮的圆心为 O，重心为 C，它们所组成的系统在竖直方向上发生自由振动的频率为 f。如果偏心轮以角速度 ω 绕 O 轴匀速转动，则当 ω =__________时振动最为剧烈，这个现象称为__________。

【答案】

2πf，共振

 

113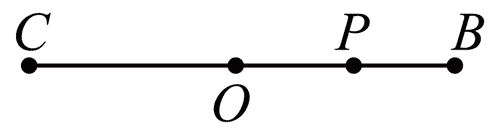．弹簧振子以 O 点为平衡位置，在 B、C 两点间做简谐运动，在 t = 0 时，振子从 OB 间的 P 点以速度 v 向 B 点运动；在 t = 0.2 s 时，振子速度第一次变为 − v；在 t = 0.5 s 时，振子速度第二次变为 − v。

（1）求弹簧振子振动的周期 T；

（2）若 B、C 之间的距离为 25 cm，求振子在 4 s 内通过的路程；

（3）若 B、C 之间的距离为 25 cm，从平衡位置计时，写出弹簧振子位移的表达式，并画出弹簧振子的振动图像。

【答案】

（1）1 s

（2）200 cm

（3）x = 12.5sin（2πt）

略

 

114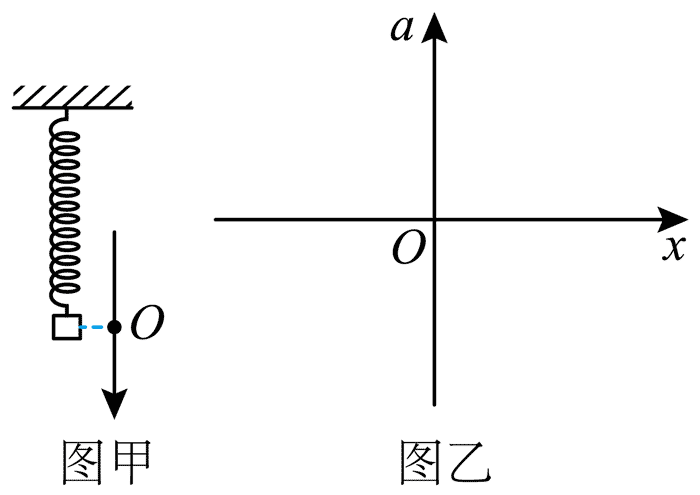．如图甲所示，劲度系数为 k 的轻质弹簧上端固定，下端连接质量为 m 的小物块。以小物块的平衡位置为坐标原点 O，以竖直向下为正方向建立坐标轴 Ox。现将小物块向上托起，使弹簧恢复到原长时将小物块由静止释放，小物块在竖直方向做往复运动，且弹簧始终在弹性限度内。

（1）求小物块的平衡位置 O 与原长的距离；

（2）以小物块经过平衡位置向下运动过程为例，通过推导说明小物块的运动是否为简谐运动；

（3）在图乙中画出由最高点运动到最低点的过程中，小物块的加速度 a 随 x 变化的图像（要求标出关键位置的坐标）。

【答案】

（1）x₀ = \(\frac{{mg}}{k}\)

（2）外物块运动到平衡位置下方 x 处，此时弹簧弹力大小 F = k（x + x₀），则小物块所受合力 F_合 = mg − F = mg − k（x + x₀）= − kx，即小物块所受合力与其偏离平衡位置的位移大小成正比，方向相反，说明小物块的运动是简谐运动。

（3）如图所示

 

115．下列说法正确的是（    ）

A．做平抛运动的物体的动量不变

B．物体的动量越大，受到的力的冲量越大

C．简谐运动系统的能量一定守恒

D．共振是有害的，因此在任何情况下都要尽可能避免共振

【答案】

C

 

116．做简谐运动的物体，相邻两次通过同一位置时，不同的物理量是（    ）

A．弹性势能          B．速度          C．加速度              D．回复力

【答案】

B

 

117．一艘在太空飞行的宇宙飞船，开动推进器后受到的推力为 2 000 N，开动 4 s 的时间，速度的改变量为 8 m/s，则宇宙飞船的质量为（    ）

A．1 000 kg           B．2 000 kg            C．3 000 kg            D．4 000 kg

【答案】

A

 

118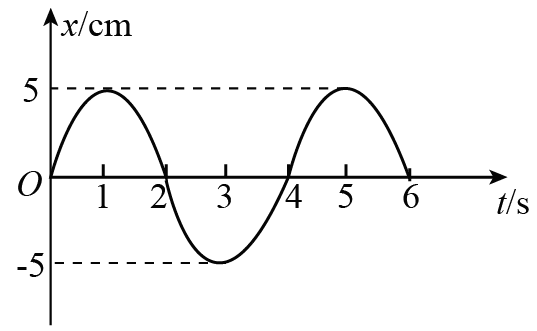．如图所示为一弹簧振子的振动图像，下列说法正确的是（    ）

A．该振子做简谐运动的频率为 4 Hz

B．第 2 s 末到第 3 s 末时间内振子的速度变大

C．第 2 s 末到第 3 s 末时间内振子的回复力变小

D．经过 100 s 振子通过的路程是 5 m

【答案】

D

 

119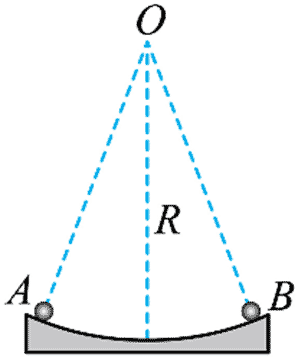．如图，小球在半径为 R 的光滑球面上的 A、B 之间做小角度的往返运动，则（    ）

A．小球的质量越大，其振动的频率越大

B．球面半径 R 越大，小球振动的频率越小

C．OA、OB 之间夹角越小，小球振动的频率越小

D．将整个装置移至正在加速上升的电梯中，小球振动的频率减小

【答案】

B

 

120．一弹簧振子的位移 y 随时间 t 变化的关系式为 y = 0.1sin（2.5πt），位移 y 的单位为 m，时间 t 的单位为 s。下列说法正确的是（    ）

A．弹簧振子的振幅为 0.2 m                                B．弹簧振子的周期为 1.25 s

C．在 t = 0.2 s 时，振子的加速度最大             D．在任意 0.2 s 内，振子的路程均为 0.1 m

【答案】

C

 

121．将总质量为 1.05 kg 的模型火箭点火升空，从静止开始，在 0.02 s 的时间内有 50 g 燃气以大小为 200 m/s 的速度从火箭尾部喷出，且燃气喷出过程中重力和空气阻力可忽略。则下列说法正确的是（    ）

A．在燃气喷出过程，火箭获得的平均推力为 800 N

B．在燃气喷出过程，火箭获得的平均推力为 200 N

C．在燃气喷出后的瞬间，火箭的速度大小约为 5 m/s

D．在燃气喷出后的瞬间，火箭的速度大小约为 10 m/s

【答案】

D

 

122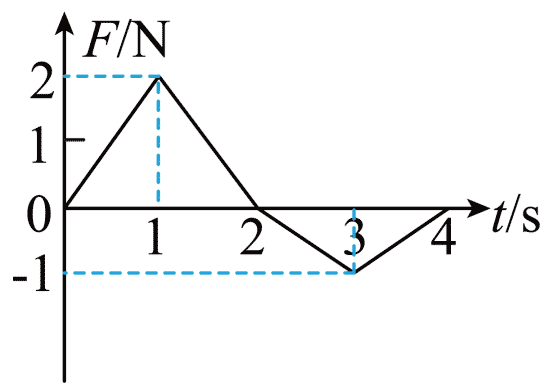．在光滑水平地面上，一质量为 1 kg 的物体在水平向右的拉力 F 作用下，由静止开始运动，拉力 F 随时间变化的关系如图所示，则下列说法正确的是（    ）

A．0 ~ 1 s 内合外力的冲量为 2 N·s                B．0 ~ 4 s 内合外力的冲量为 1 N·s

C．t = 1 s 时，物体的速度最大                           D．t = 4 s 时，物体的速度为零

【答案】

B

 

123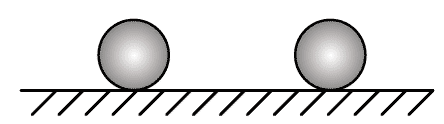．如图，光滑水平面上有大小相同的 A、B 两球在同一直线上运动。两球质量关系为 m_B = 2m_A，规定向右为正方向，A、B 两球的动量均为 10 kg·m/s，运动中两球发生碰撞，碰撞后 A 球的动量为 6 kg·m/s，则（    ）

A．左方是 A 球，碰撞后 A、B 两球速度大小之比为 2∶5

B．左方是 A 球，碰撞后 A、B 两球速度大小之比为 6∶7

C．右方是 A 球，碰撞后 A、B 两球速度大小之比为 2∶5

D．右方是 A 球，碰撞后 A、B 两球速度大小之比为 6∶7

【答案】

B

 

124．简谐运动中平衡位置的回复力__________为零，合外力__________为零，加速度__________为零。（均选填“一定”或“不一定”）

【答案】

一定，不一定，不一定

 

125．摆角小于 5°__________（选填“是”或“不是”）建立单摆模型的条件之一。保持某个单摆的摆线长度不变，摆球换成密度相同、质量 4 倍的球，该单摆做简谐运动的周期会__________（选填“增大”“减小”或“不变”）。

【答案】

是，增大

 

126．质量为 0.4 kg 的小球以 6 m/s 的速度竖直向下撞击水平地面，与地面作用时间为 0.25 s 后再以 4 m/s 的速度反向弹回。取竖直向上为正方向，则小球与地面碰撞前后的动量变化为__________kg·m/s，碰撞过程中小球受到地面作用力的冲量大小为__________N·s。

【答案】

4，5

 

127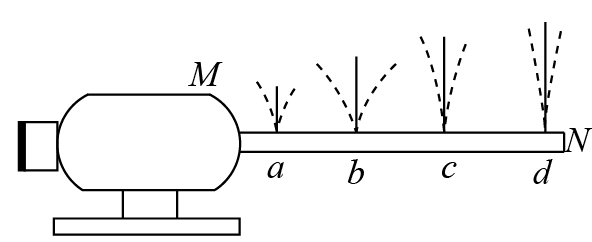．如图所示是用来测量各种电动机转速的转速计原理图。在同一铁支架 MN 上焊有固有频率依次为 100 Hz、90 Hz、80 Hz、70 Hz 的四个钢片 a、b、c、d，将 M 端与正在转动的电动机接触，发现 b 钢片振幅很大，其余钢片振幅很小，则 a、b、c、d 此时振动频率为__________Hz，电动机的转速为__________r/min。

【答案】

90，5 400

 

128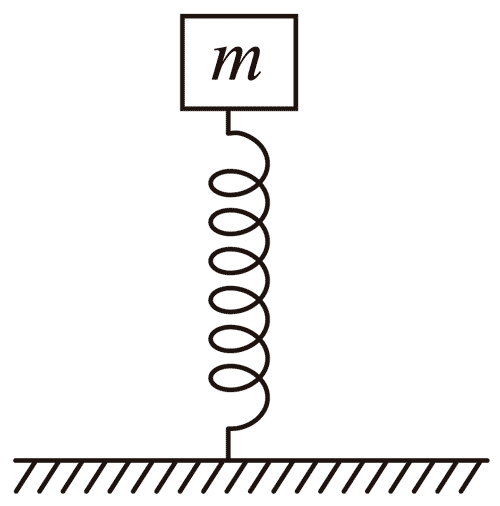．如图，质量为 m 的木块放在轻质弹簧上，与弹簧一起在竖直方向上做简谐运动。当振幅为 A 时，物俸对弹簧的最大压力是物体重力的 1.5 倍，则物体对弹簧的最小弹力为__________；要使物体在振动中不离开弹簧，振幅的最大值为_________。

【答案】

0.5mg，2A

 

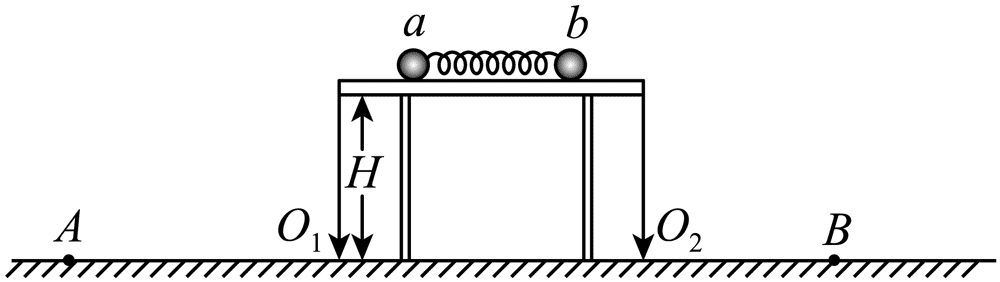
129．b 之间用细线连接，中间夹一个被压缩的轻质弹簧（弹簧原长小于桌面宽度，不考虑空气阻力对球运动的影响）。剪断细线，观察两球的运动情况，进行必要的测量，验证两球相互作用过程中是否动量守恒。

（1）（多选）本实验必须测量的物理量是（    ）

A．桌面到水平地面的高度 H

B．小球 a、b 的质量 m_a、m_b

C．小球 a、b 离开桌面后在空中飞行的时间 t

D．记录纸上 O₁ 点到 a 球落地点 A 的距离 O₁A，O₂ 点到 b 球落地点 B 的距离 O₂B

（2）用测得的物理量验证动量守恒的关系式为_____________________________；

（3）此装置还可用来测剪断细线前弹簧的弹性势能 E_p，则 E_p = __________（用 m_a、m_b、H、O₁A、O₂B、g 表示）。

【答案】

（1）BD

（2）m_a·O₁A = m_b·O₂B

（3）\(\frac{g}{{4H}}\)（m_a·O₁A² + m_b·O₂B²）

 

130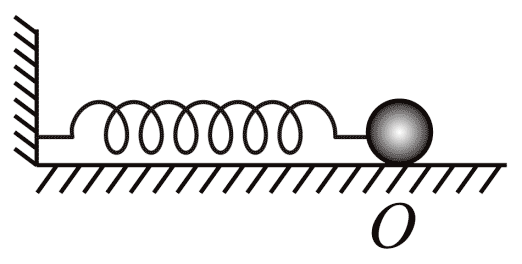．如图，弹簧振子放在光滑水平桌面上，O 点处是平衡位置，振幅 A = 2 cm，周期 T = 0.4 s。

（1）若以向右为位移的正方向，当振子运动到 O 点右侧最大位移处开始计时，试画出其一个周期的振动图像；

（2）若从振子经过平衡位置开始计时，求经过 2.6 s 振子通过的路程；

（3）若从振子经过平衡位置开始计时，定性描述半个周期内弹簧振子各种形式的能量的变化过程。

【答案】

（1）如图

（2）0.52 m

（3）弹簧振子的动能先减小后增大，弹性势能先增大后减小

 

131．某机车关闭发动机后以 0.4 m/s 的速度驶向停在铁轨上并互相间隔一定距离的若干节车厢，与它们一一对接。机车与第一节车厢相碰后它们连在一起共同运动，紧接着又与第二节车厢相碰，就这样，直至碰上最后一节车厢的共同速度为 0.05 m/s。设机车和车厢的质量都相等，机车和车厢运行过程中一切阻力忽略不计。

（1）列车一共有多少节车厢？

（2）若机车与第一节车厢相碰时相互作用的时间是 0.02 s，求碰撞过程中平均作用力和车厢重力的比值。

【答案】

（1）n = 7

（2）1

 

132．振动的物体都具有周期性，若简谐运动的弹簧振子的周期为 T，则它的动能、势能变化的周期为（    ）

A．2T             B．T                C．\(\frac{T}{2}\)              D．\(\frac{T}{4}\)

【答案】

C

 

133．一个弹簧振子，第一次被压缩 x 后释放做自由振动，频率为 f₁；第二次被压缩 2x 后释放做自由振动，频率为 f₂ 则（    ）

A．f₁ > f₂                 B．f₁ = f₂         C．f₁ < f₂         D．不能确定

【答案】

B

 

134．某单摆在做小角度摆动，下列做法会改变它的周期大小的是（    ）

A．仅增大摆球质量

B．仅减小摆角

C．在摆球上施加一个竖直向下的恒力

D．让摆球带正电，悬点处也有一带正电的小球

【答案】

C

 

135．摆长为 l 的单摆做简谐运动，若从某时刻开始计时（取 t = 0），当振动至 t = \(\frac{{3\pi }}{2}\sqrt {\frac{l}{g}} \) 时，摆球恰具有负向最大速度，则单摆的振动图像是（    ）

【答案】

C

 

136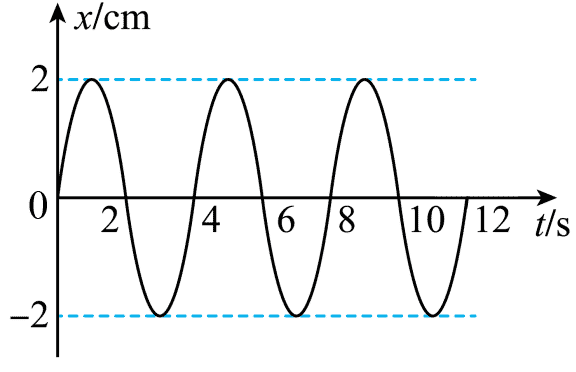．质点做简谐运动的振动图像如图所示，下列说法正确的是（    ）

A．质点振动的频率是 4 Hz

B．第 2 s 末质点的速度为零

C．在 4 s 内质点经过的路程是 8 cm

D．在 t = 3 s 和 t = 5 s 两时刻，质点的位移大小相等、方向相同

【答案】

C

 

137．一炮弹质量为 m，以斜向上、与水平面成 60° 角的初速度 v 发射，炮弹在最高点爆炸成两块，其中质量为 \(\frac{m}{3}\) 的一块恰好做自由落体运动，另一块的瞬时速度大小为（    ）

A．\(\frac{3v}{4}\)            B．\(\frac{3v}{8}\)            C．2v              D．\(\frac{4v}{3}\)

【答案】

A

 

138．如图，学生练习用头颠球。某一次足球从静止开始下落 20 cm，被头竖直顶起，离开头部后上升的最大高度仍为 20 cm。已知足球与头部的作用时间为 0.1 s，足球的质量为 0.4 kg，不计空气阻力。下列说法正确的是（    ）

A．头部对足球的平均作用力为足球重力的 5 倍

B．在与头部作用的过程中，足球动量变化量大小为零

C．下落到与头部刚接触时，足球动量大小为 1.6 kg·m/s

D．从最高点下落至重新回到最高点的过程中，足球重力的冲量为零

【答案】

A

 

139．如图，物体 m 系在两水平弹簧之间，两弹簧的劲度系数分别为 k₁ 和 k₂，且 k₁ = k，k₂ = 2k，两弹簧均处于自然伸长状态。向右拉动 m，然后释放，物体在 B、C 间振动（不计阻力），O 为平衡位置，则下列判断正确的是（    ）

A．m 做简谐运动，OC > OB                      B．m 做简谐运动，OC < OB

C．回复力 F = − kx                                        D．回复力 F = − 3kx

【答案】

D

 

140．弹簧振子做简谐运动，O 为平衡位置，当它经过点 O 时开始计时，经过 0.3 s 第一次到达点 M，再经过 0.2 s 第二次到达点 M，则弹簧振子第三次到达点 M 还要经过的时间可能为（    ）

A．\(\frac{1}{2}\) s            B．\(\frac{8}{15}\) s          C．1.4 s          D．1.6 s

【答案】

C

 

141．如图，在光滑水平地面上，A、B 两物体的质量都为 m，A 以速度 v 向右运动，B 左端有一轻质弹簧且初速度为零，在 A 与弹簧接触以后的过程中（A 与弹簧不粘连），下列说法正确的是（    ）

A．A、B 组成的系统机械能守恒

B．轻质弹簧被压缩到最短时，A 的动能为 \(\frac{1}{4}\)mv²

C．轻质弹簧被压缩到最短时，A、B 组成的系统的总动量小于 mv

D．弹簧恢复原长时，A 的动量为零

【答案】

D

 

142．如图，小球甲、乙分别以速度 v₁、v₂ 从斜面顶端抛出并落在斜面上，且竖直方向位移分别为 h₁、h₂，另一小球丙相对斜面抛出，与小球甲落在斜面上同一位置，其竖直方向位移为 h₃，三小球质量都相同。下列说法正确的是（    ）

A．若 h₁ = h₃，则甲、丙两小球落在斜面瞬间的动量大小相同

B．若 v₁ ≠ v₂，则甲、乙两小球末动量大小、方向都不相同

C．若 h₁ = h₃，则甲、丙两小球落在斜面瞬间的重力冲量相同

D．三小球不可能同时落在斜面上

【答案】

C

 

143．秒摆的频率为_________Hz，北京使用的秒摆摆长_________（选填“大于”或“小于”）广州使用的秒摆摆长。

【答案】

0.5，大于

 

144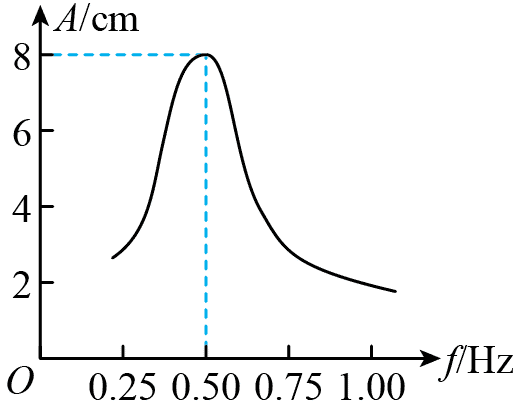．如图所示为一个单摆的共振曲线。由图可知该单摆共振时的振幅为_________cm，该单摆的固有周期为_________s。

【答案】

8，2

 

145．如图，弹簧振子的振动周期为 2 s，由 C 点向 B 点开始振动，并从 O 点开始计时，若振幅为 2 cm，则在 3.5 s 内振子通过的路程为_________cm，3.4 s 末振子正在向_________点运动（选填“C”“O”或“B”）。

【答案】

14，C

 

146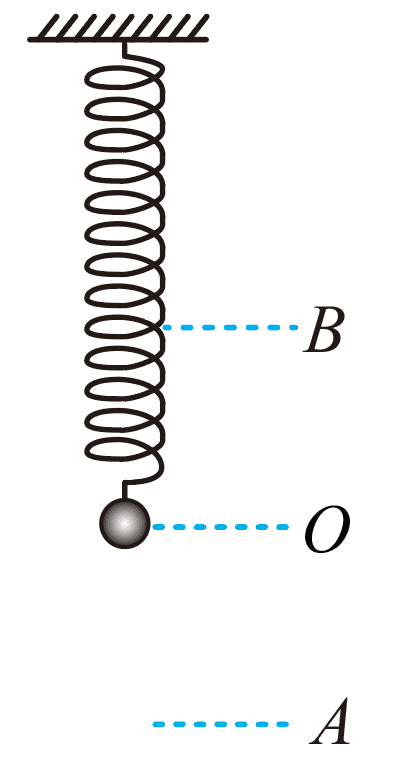．如图，弹簧振子竖直悬挂，振子质量 m = 0.1 kg，劲度系数 k = 10 N/m，静止时振子处在点 O 的位置，现给振子一个向上的初速度，经过 \(\frac{{\pi }}{5}\) s 振子到最高点 B 时弹簧刚好恢复原长。求：

（1）振子振动的振幅、周期；

（2）从点 O 运动开始计时，经过时间 t = \(\frac{{21\pi }}{5}\) s 的路程；

（3）振子运动到最低点 A 的回复力。

【答案】

 （1）0.1 m，0.8π s

（2）2.1 m

（3）1 N，方向向上

 

147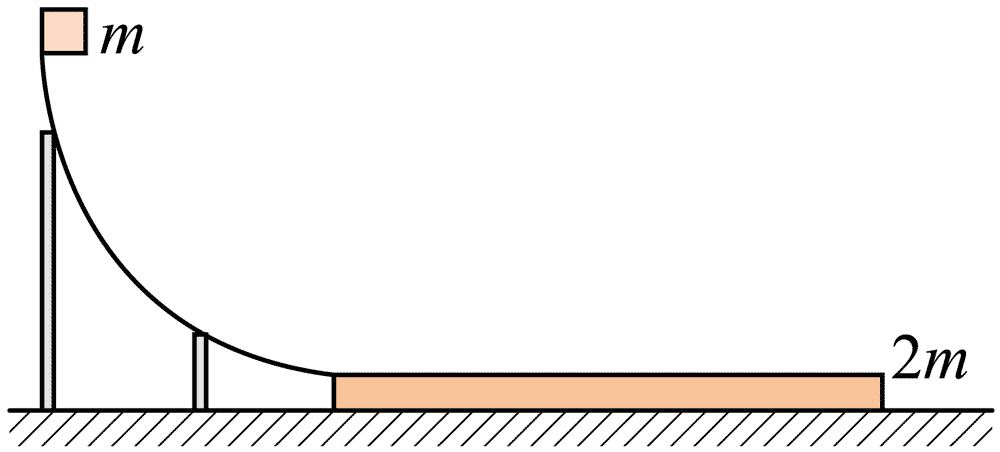．如图，将质量为 0.4 kg 的长木板静止放置在光滑的水平面上，在其左侧竖直面内固定一个半径 r = 1.8 m 的四分之一光滑圆弧轨道，轨道的最低点切线水平且与长木板等高，让质量为 0.2 kg 的木块从轨道的最高点由静止开始下滑，最终木块刚好不离开长木板，已知木块与长木板之间的滑动摩擦力大小 f = 0.8 N。求：

（1）木板的长度；

（2）木块在木板上的滑行时间；

（3）木块从静止开始下落到稳定运动，合力对其冲量为多少？

【答案】

（1）L = 3 m

（2）0.4 N·s