1．下列物理量中属于矢量的是（    ）

A．振幅          B．周期    C．功率          D．加速度

【答案】

D

 

2．爱因斯坦在物理学中的重要贡献有（    ）

A．发现万有引力定律                          B．建立狭义相对论

C．首次测定元电荷的电荷量              D．最早发现电磁感应现象

【答案】

B

 

3．在国际单位制（SI）中，“电势”用基本单位可以表示为 （    ）

A．kg·m²·s⁻²          B．kg·m·C⁻¹          C．kg·m²·A⁻¹·s⁻³           D．kg·m²·C⁻¹·s⁻³

【答案】

C

 

4．关于电动势和电压的理解，下列说法正确的是（    ）

A．电源两极间的电压就是电源的电动势

B．家用 5 号干电池的电动势大于 7 号干电池的电动势

C．两者单位都是伏特，故电动势与电压属于同一物理量

D．电动势的大小反映电源把其它形式能量转化为电能的本领

【答案】

D

 

5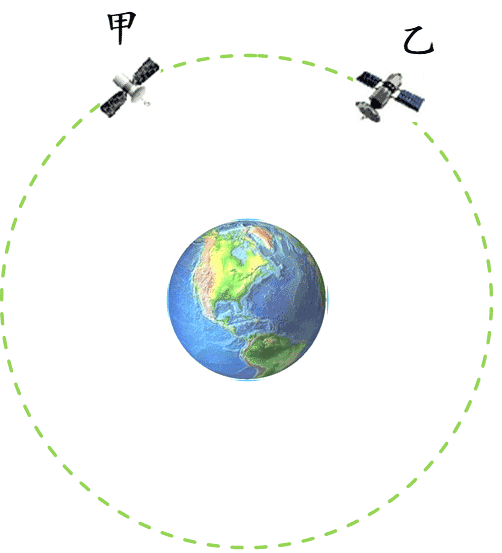．如图，甲、乙两颗人造地球卫星在同一圆形轨道上绕地球运行，则两颗卫星（    ）

A．动能一定相同

B．周期一定相同

C．加速度一定相同

D．受地球的引力一定相同

【答案】

B

 

6．从某高处释放一粒小石子，经过 2 s 从同一地点再释放另一粒小石子。不计空气阻力，落地前，两粒石子间的距离将（    ）

A．保持不变         B．不断减小         C．不断增大         D．先增大后减小

【答案】

C

 

7．宇航员在图示的天宫空间站内将冰墩墩抛出，则（    ）

A．冰墩墩处于完全失重状态，是因为其不受重力

B．冰墩墩在飞行过程中，所受外力的合力不为零

C．冰墩墩在飞行过程中，因为不受力，所以做匀速直线运动

D．抛掷瞬间，宇航员对冰墩墩的作用力大于冰墩墩对宇航员的作用力

【答案】

B

 

8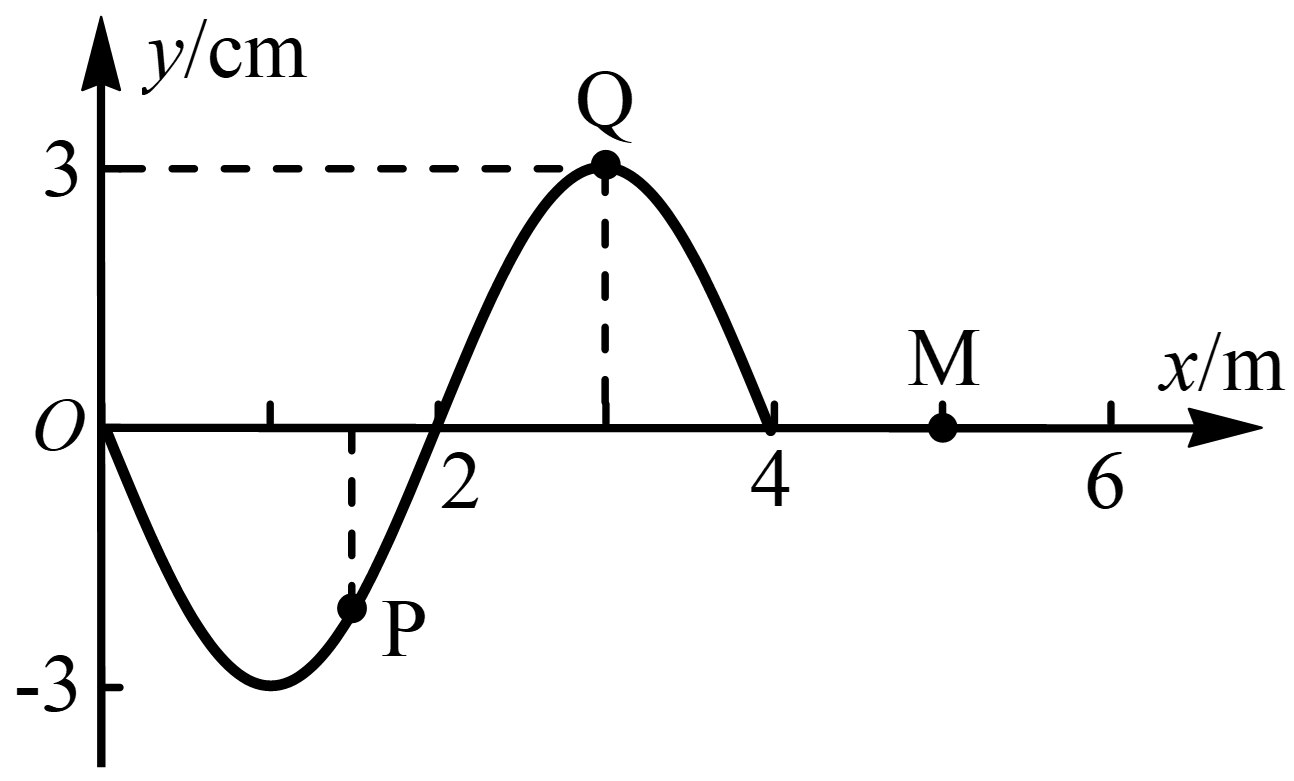．图示为 t = 0时刻的波形图，波速 v = 2 m/s。从图示时刻开始，质点 Q 领先于质点 P 到达平衡位置。则（    ）

A．波沿 x 轴负方向传播

B．质点 P 的振动周期 T = 4 s

C．t = 1.5 s 时，质点 P 和 Q 均沿 y 轴正方向运动

D．t = 0 到 1.5 s 的时间内，质点 M 通过的路程为 6 cm

【答案】

D

 

9．如图，O 点固定一个点电荷 + Q，绝缘细线将另一带电小球 + q 悬挂于 O 点。将小球 + q 轻轻拉至 A 点，由静止释放后，小球在 A、B 间做小幅摆动，不计空气阻力。当小球 + q 向左经过最低点 C 时，迅速移走点电荷 + Q，则（    ）

A．摆动周期减小

B．小球仍能到达 B 点

C．再次经过 C 点时，小球的速度大于此前经过 C 点时的速度

D．再次经过 C 点时，细线的张力大于此前经过 C 点时的张力

【答案】

B

【解析】

选项 AB：由于带电小球之间的库仑力始终沿绳方向，对圆弧切线方向的回复力没有影响，因此单摆的周期、振幅都不会发生变化。选项 A 错误、B 正确；

选项 C：库仑力始终垂直于运动方向，不做功，小球的机械能仍然不变，经过 C 的速度大小也不变；

选项 D：在最低点 C，沿绳方向原来有一个向下的库仑斥力，移走电荷后此力消失，导致细线的拉力变小。选项 D 错误。

正确选项为 B。

 

10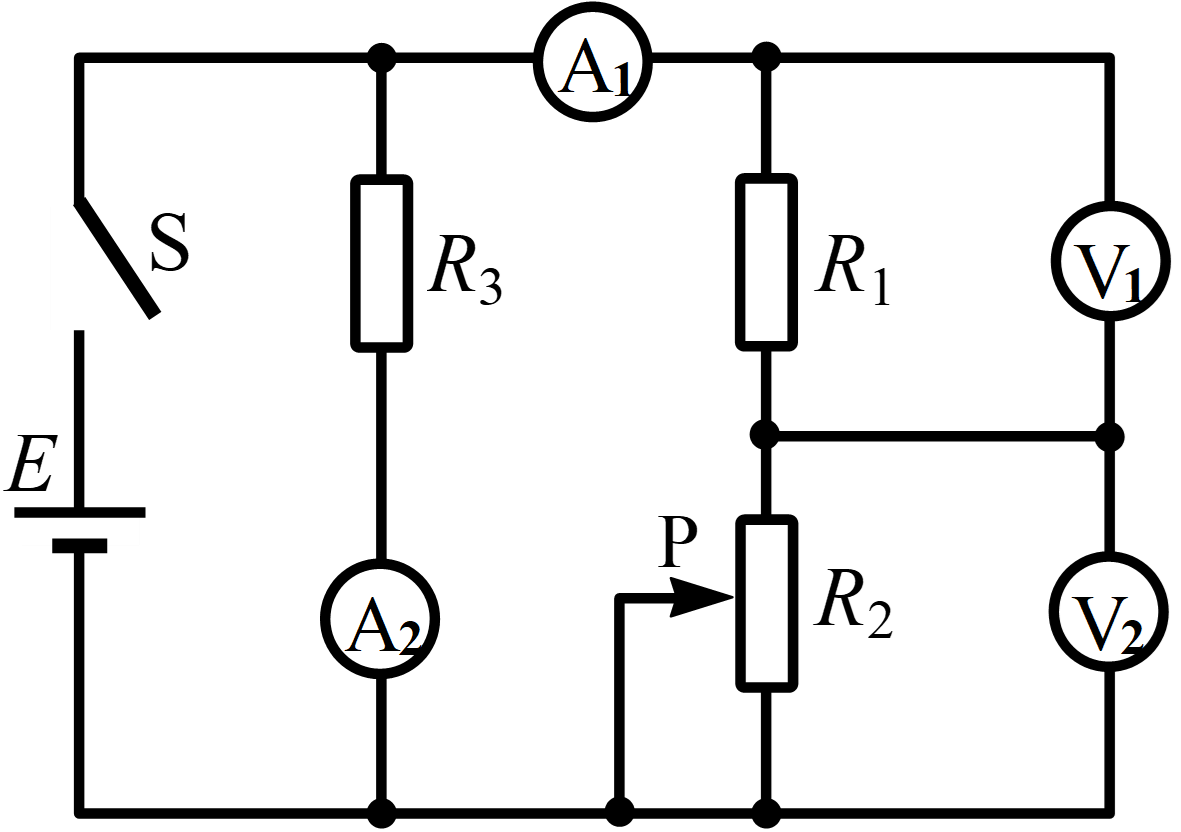．图示电路中，电源电动势为 E，内阻不计。闭合开关 S，滑动头 P 由中点向下移动的过程中，电表 A₁、V₁、V₂ 示数变化的大小分别为 ΔI₁、ΔU₁、ΔU₂，则（    ）

A．A₁ 示数减小、A₂ 示数增大

B．A₁ 示数减小，A₂ 示数不变

C．\(\frac{{\Delta {U_1}}}{{\Delta {I_1}}}\) 不变，\(\frac{{\Delta {U_2}}}{{\Delta {I_1}}}\) 增大

D．\(\frac{{\Delta {U_1}}}{{\Delta {I_1}}}\)、\(\frac{{\Delta {U_2}}}{{\Delta {I_1}}}\) 均不变，且 \(\frac{{\Delta {U_1}}}{{\Delta {I_1}}}\) < \(\frac{{\Delta {U_2}}}{{\Delta {I_1}}}\)

【答案】

B

【解析】

选项 AB：滑片向下移动的过程中，R₂ 变大，总电阻变大，干路电流 I 变小；由于内阻不计，端电压 U 不变，因此通过 R₃ 的电流 I₃ 不变，即 A₂ 示数不变；而通过 R₁ 的电流 I₁ = I – I₃ 可知 A₁ 的示数减小。选项 A 错误，B 正确；

选项 CD：\(\frac{{\Delta {U_1}}}{{\Delta {I_1}}}\) = R₁ 是不变的。由于端电压 U 不变，且 U = U₁ + U₂，可以得出 ΔU₁ = ΔU₂，进一步可以得出 \(\frac{{\Delta {U_1}}}{{\Delta {I_1}}}\) = \(\frac{{\Delta {U_2}}}{{\Delta {I_1}}}\) = R₁ 且不变的结论。选项 C、D 都是错误的

正确选项为 B。

 

11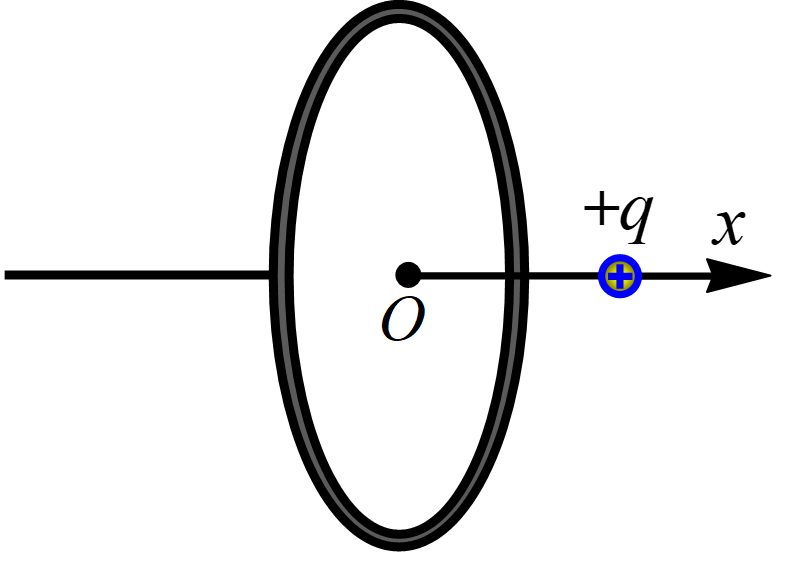．如图，圆环均匀带正电，沿其中心轴线建立 x 轴。将另一点电荷 + q 从圆心 x = 0 处沿 x 轴正方向移到无穷远处的过程中，电场力做功为 W₀。取无穷远处为电势能零点，则电荷 + q 具有的电势能 E_p 与位置坐标 x 的关系图像正确的是（    ）

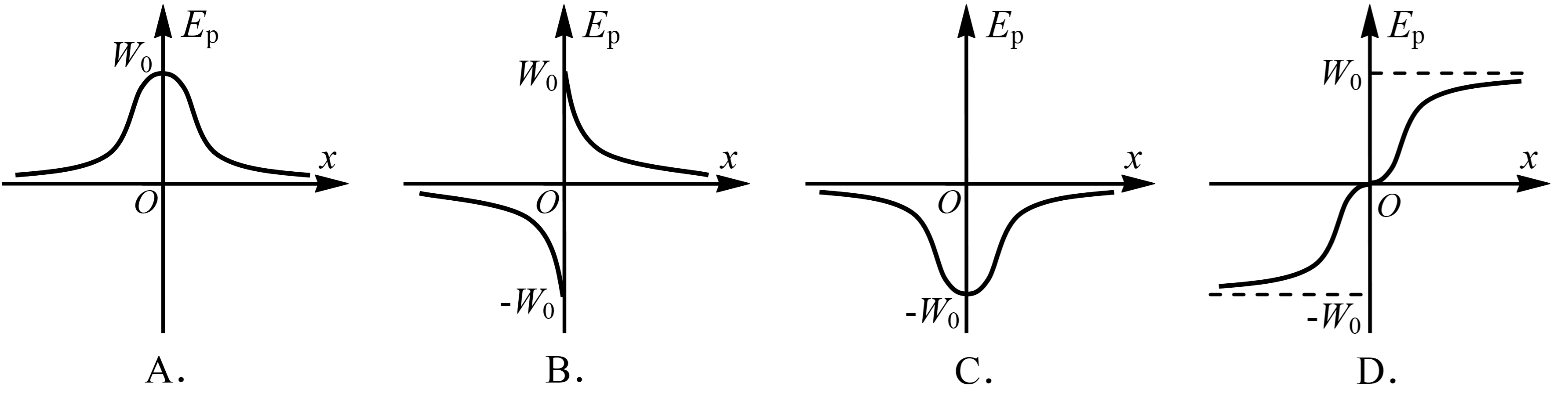
【答案】

A

 

12．如图，飞行员通过手柄控制推力 F 的大小和方向，可以改变单人滑板式飞行器在空中的飞行方向和速度。调节推力 F，使飞行器沿与竖直成 θ 角的方向匀速飞行（θ < 90°），飞行员受到空气的阻力与其速度成正比，则（    ）

A．推力 F 沿飞行方向指向左上方

B．飞行方向不变，速度越大，推力 F 与竖直方向夹角越小

C．若保持推力 F 方向不变，匀速飞行的速度较大时，θ 角较小

D．若保持推力 F 大小不变，匀速飞行的速度较大时，θ 角较小

【答案】

C

【解析】

由于飞行器匀速飞行，则它在其重力 G、空气阻力 f、推力 F 作用下处于受力平衡状态，受力情况如图所示。

A．由受力图可知推力 F 并不沿飞行方向。选项 A 错误；

B．速度越大，空气阻力 f 越大，由图可知，F 与竖直方向的夹角越大。选项 B 错误；

C．由图可知，速度较大时 f 也较大，即图中对应 f 的邻边变长，要使对应 F 的对角线方向不变，此邻边应顺时针旋转，即 v 方向顺时针旋转，θ 变小。选项 C 正确。

D．由图可知，速度较大时对应 f 的邻边变长，要使对应 F 的对角线长度不变，应使 θ 变大。选项 D 错误。

 

13．静电场是________________周围空间存在的一种物质；描述电场力的属性和能的属性的物理量分别为_________________、_________________。

【答案】

 静止电荷，电场强度、电势

 

14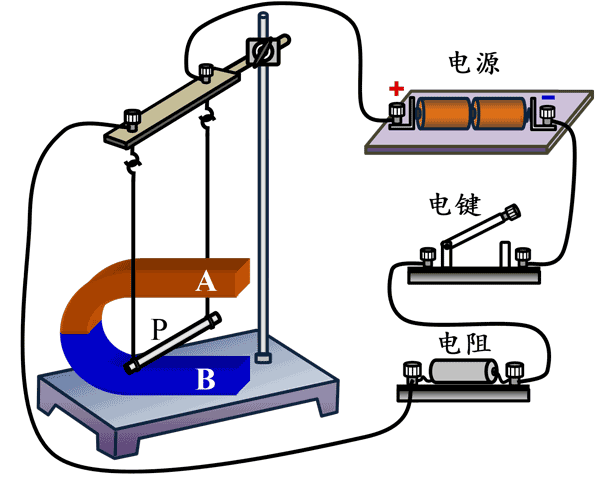．图示为研究左手定则的实验装置图。闭合电键，铜棒 P 向右摆动，则 U 型磁铁的 A 端为________极（选填“N”或“S”）。铜棒 P 从静止开始起，第一次到达右侧最高点的过程中，不计空气阻力，其机械能________________（选填“增大”、“减小”、“先增后减”、“先减后增”）。

【答案】

N，增大

 

15．跳水比赛中，运动员向上离开踏板的瞬间为计时起点，竖直向上为正方向。运动员可看做质点，其竖直方向的速度 v 与时间 t 的关系如图所示，则运动员到达最高点的时刻为___________，踏板距离水面的高度为_________m。

【答案】

0.5 s，10

 

16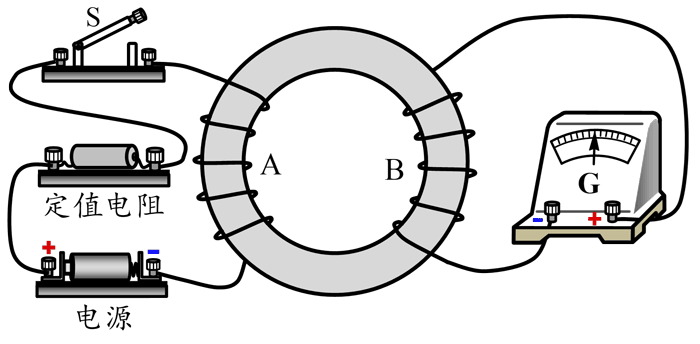．图示为研究电磁感应现象的实验装置图，A、B 是套在同一圆形铁芯上的两个线圈。事先已经探明：电流从正极流入灵敏电流计 G 时，指针向右偏转。现将电键 S 闭合，再稳定一段时间，观察到电流计的指针先______________，最后回到中间位置不动。指针回到中间不再偏转的原因是：_________________________________________________________________。

【答案】

向左偏转。电路接通稳定后，线圈 A 产生磁场虽然最强但恒定不变，穿过线圈 B 的磁通量最大但不变，感应电流消失，电流计的指针不再偏转。

 

17．图（甲）中，粗糙程度相同的斜面固定在地面上，将小物块从斜面顶端由静止释放，经 6 s 匀加速下滑到底端。图（乙）中的 ①、② 两条曲线分别表示该过程重力、摩擦力对物块做功随时间的变化关系，虚线 AB 为 t = 6 s 时曲线 ① 的切线，则切线 AB 斜率的物理意义是___________________________________。以地面为重力势能零势能面，当物块重力势能 E_p = 9 J 时，其动能 E_k = _______J。

【答案】

t = 6 s 时重力的瞬时功率（答“t = 6 s 时重力势能的变化率”、“t = 6 s 时重力势能变化的快慢”的，同样给分），6

【解析】

（1）由 P = \(\frac{W}{t}\) 可知，W – t 图像斜率的物理意义即功率，切线斜率即对应时刻的瞬时功率；

（2）由图可知，小物块从顶端滑至底端，重力做功 18 J，克服摩擦力做功 6 J。当重力势能为 9 J 时，即物块滑至斜面中点。由 W_G = mgsinθ·s、W_f = − fs 可知，W_G 与 W_f 成正比关系，因此物块滑至斜面中点的过程中，重力做功 9 J，克服摩擦力做功应为 3 J，根据动能定理可知此时刻动能为 6 J。

 

18．在“用 DIS 测量电源的电动势和内阻”的实验中，A 同学将待测电源、电阻箱 R、阻值为 6 Ω 的定值电阻 R₀、电流传感器连成图（甲）所示的电路。

（1）B 同学认为：R₀ 阻值太小，可以去掉。你___________B 同学的观点（选填“赞同”、“不赞同”），理由是：_____________________________________。

（2）A 同学实验时，调整电阻箱的阻值，记录多组电阻箱的阻值 R 和电流传感器示数 I，在计算机上绘出 \(\frac{1}{I}\) - R 关系图线，如图（乙）中的线 a 所示。将电源 a 换为电源 b，测量多组数据，在同一坐标系中绘出图线 b。

    

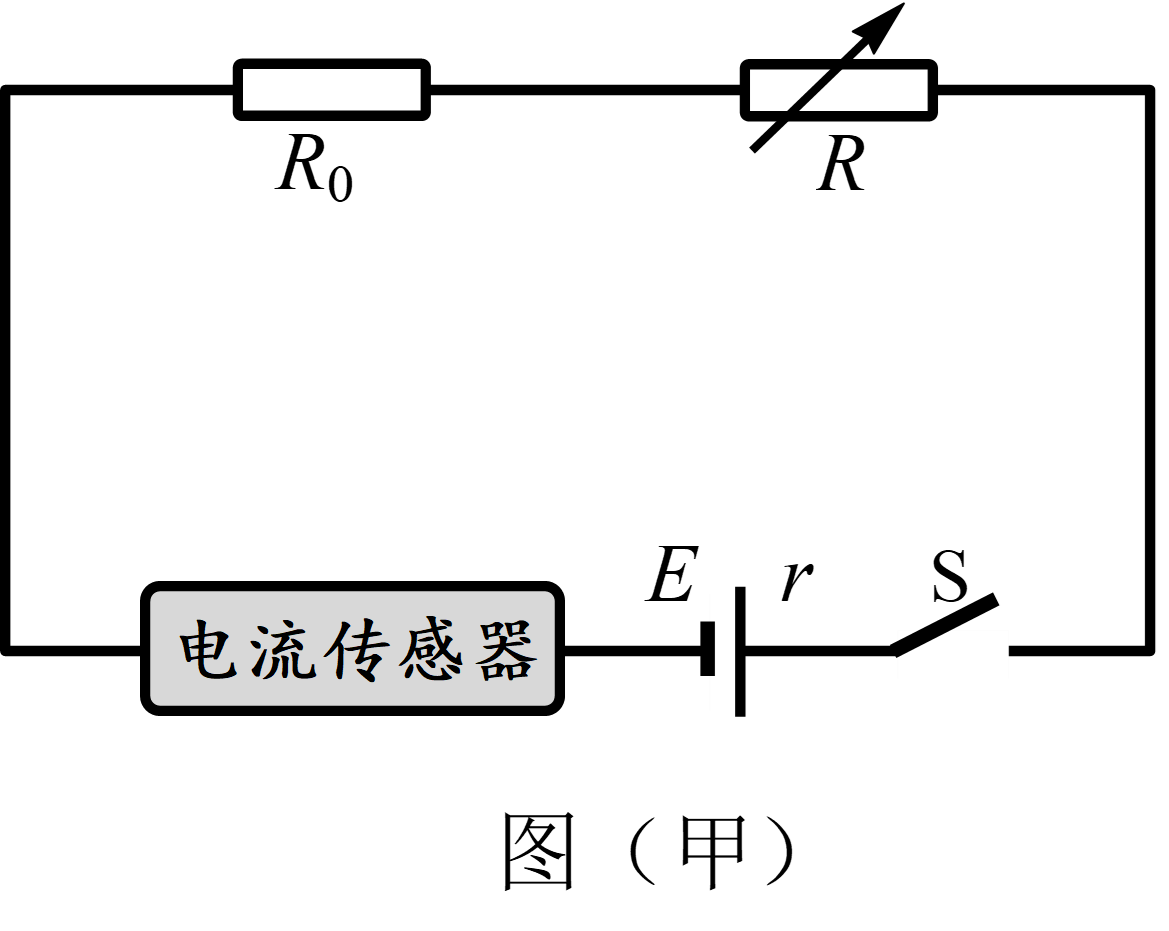
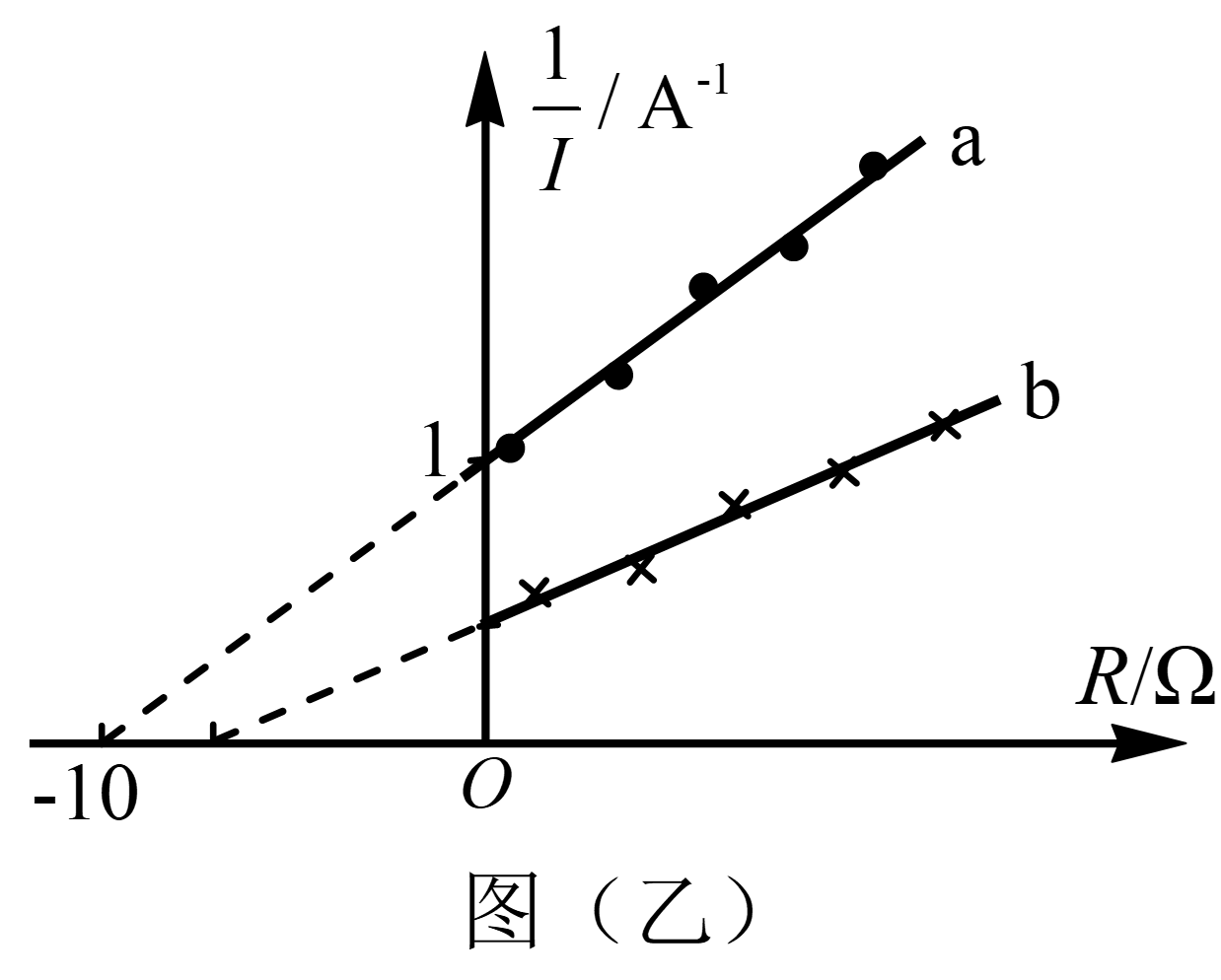
①不计电流传感器的内阻，依据图线可知，电源 a 的电动势 E_a = _________V，内阻 r_a = _______Ω。

②若将定值电阻 R₂ 分别与电源 a、b 连接，则 R₂ 两次消耗的功率 P_a_______P_b（选填“大于”、“等于”或“小于”）。

【答案】

（1）不赞同。若无 R₀，调节 R 的过程中，电源可能被短路，损坏电源或电流传感器。

（2）① 10 V，4 Ω；

② 小于

 

19．如图，长度为 2l 的光滑直杆 AB 固定在水平地面，与水平面的夹角 θ = 30°，质量为 m 的小球套在杆上。原长为 l 的轻质橡皮筋下端固定在 A 点正下方的 O 点，上端与球相连。将小球从 A 点由静止释放，运动到底端 B 时速度恰为零，橡皮筋始终在弹性限度内，重力加速度为 g。求：

（1）运动到杆的中点 C 时，小球速度 v_C 的大小；

（2）运动到杆的中点 C 时，小球重力的功率 P_G；

（3）请分析说明：小球从 A 到 B 的过程中，其动能是如何变化的？

【答案】

（1）v_C = \(\sqrt {gl} \)

（2）P_G = \(\frac{1}{2}\) mg \(\sqrt {gl} \)

（3）动能先增大后减小

【解析】

（1）因 OC = OA，故小球运动到 C 点之前的过程中，橡皮筋处于松弛状态，其弹力为零，

机械能守恒：mglsinθ = \(\frac{1}{2}\)mv_C²，

解出：v_C = \(\sqrt {2gl\sin \theta } \) = \(\sqrt {gl} \)

（2）重力的瞬时功率 P_G = mgv_Csinθ = \(\frac{1}{2}\) mg \(\sqrt {gl} \)

（3）A 到 C 的过程中：

橡皮筋弹力为零，小球仅受重力、支持力，匀加速下滑，动能增大；

C 到 B 的过程中：

小球受重力 mg、支持力 F_N、橡皮筋弹力 F_f 的作用，如图。 

     

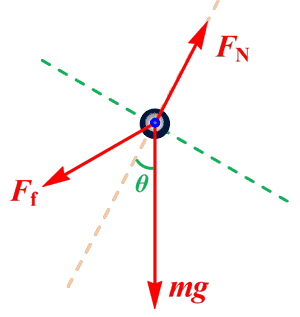
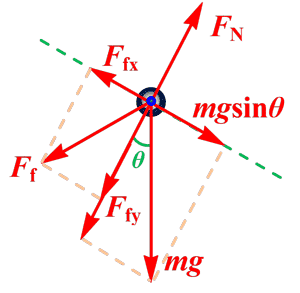
橡皮筋弹力 F_f 逐渐增大，沿杆向上的分力 F_fx 逐渐增大，

最初，F_fx ≤ mgsinθ，合外力沿杆向下，继续加速向下运动，动能增大；

此后，F_fx > mgsinθ，合外力沿杆向上，减速运动，动能减小；

故 A 到 B 的过程中，小球的动能先增大后减小。

 

20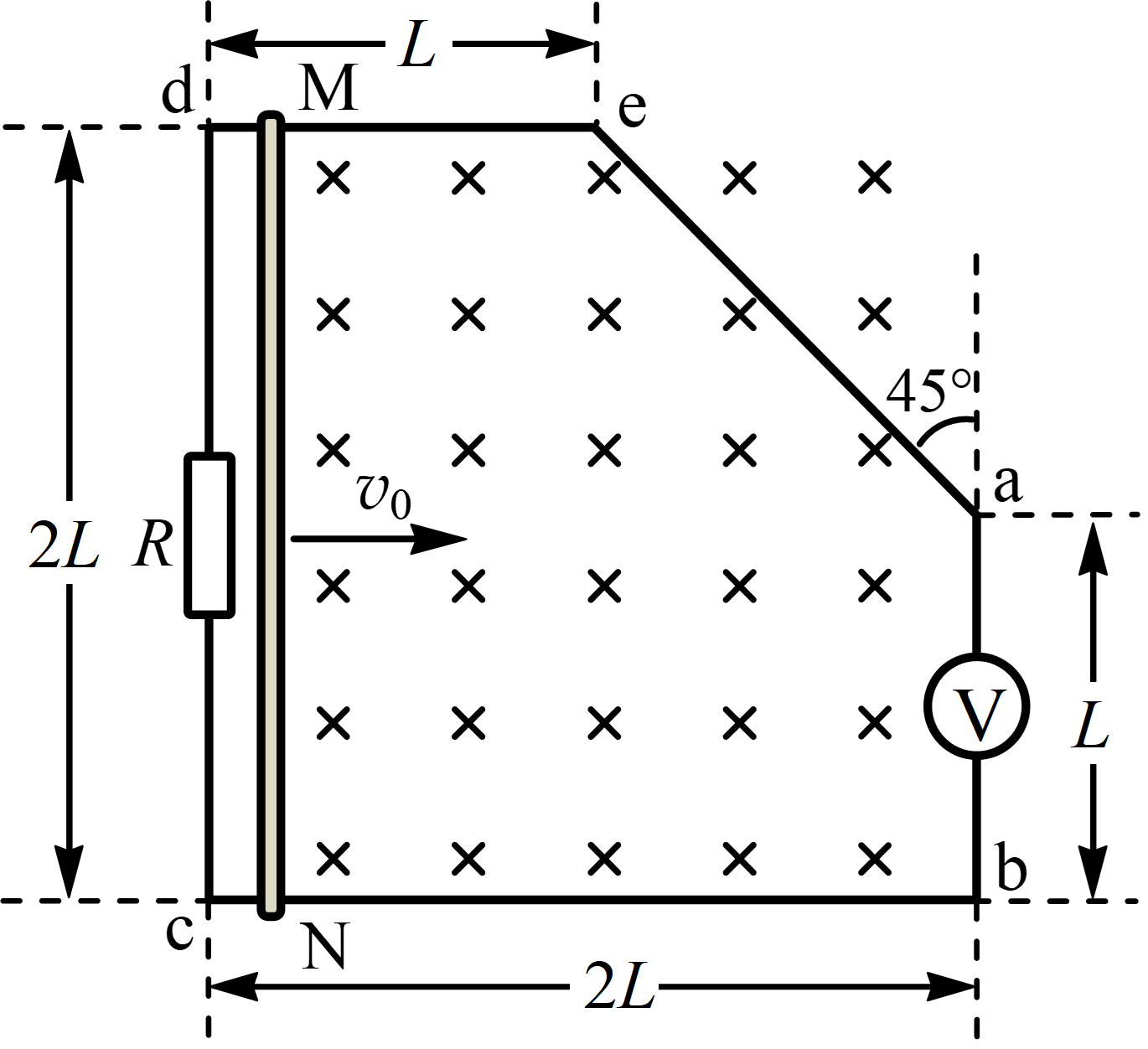．光滑金属框架 abcde 置于水平面内，∠b = ∠c = ∠d = 90°，各边长度如图所示。Cd 边接入阻值为 R 的定值电阻，ab 边接入电压表 V，导体棒 MN 平行于 cd，不计框架与导体棒的电阻。匀强磁场垂直于框架平面，磁感应强度大小为 B。在外力作用下，MN 沿框架以初始速度 v₀ 从靠近 cd 的位置向右运动，导体棒始终与 bc 垂直且接触良好。MN 运动到 ab 之前的过程中，电压表的示数恒为 U。

（1）试从功和能量转化关系的角度证明：MN 在 d、e 之间运动的过程中，切割磁感线产生的电动势 E = 2BLv₀；

（2）若定义“另类加速度”为通过单位位移内的速度改变量，用公式表示为 A = \(\frac{{\Delta v}}{{\Delta s}}\)。请分析说明：MN 向右运动的整个过程中，A 是如何变化的？

（3）MN 由 cd 向右运动到 ab 的过程中，安培力对导体棒所做的功 W_A 为多少？

【答案】

（1）导棒向右切割磁感线的过程中，克服安培力做功，将其他形式的能量转化为电能。

故：克服安培力做功等于电能的增加量，即：F_A·s = EIt

安培力 F_A = BI·(2L)

由于不计导棒电阻，故电动势等于路端电压，即 E = U

导棒在 d、e 之间时，路端电压、电动势不变，切割磁感线的长度为 2L 也不变，导棒应匀速运动，t 内的位移 s = v₀t

将 F_A = BI·(2L) 和 s = v₀t 带入 F_A·s = EIt，即可得到 E = 2BLv₀

（2）A 先不变后增大

（3）W_A = − \(\frac{{7BU{L^2}}}{{2R}}\)

【解析】

（1）导棒向右切割磁感线的过程中，克服安培力做功，将其他形式的能量转化为电能。

故：克服安培力做功等于电能的增加量，即：F_A·s = EIt

安培力 F_A = BI·(2L)

由于不计导棒电阻，故电动势等于路端电压，即 E = U

导棒在 d、e 之间时，路端电压、电动势不变，切割磁感线的长度为 2L 也不变，导棒应匀速运动，t 内的位移 s = v₀t

将 F_A = BI·(2L) 和 s = v₀t 带入 F_A·s = EIt，即可得到 E = 2BLv₀

（2）当位移 s ≤ L 时，U = 2BLv₀，速度 v = v₀ = \(\frac{U}{{2BL}}\) 不变。故 A = 0，不变；

当位移 L ≤ s ≤ 2L 时，MN 接入电路的有效长度为 (3L − s)，

由 U = B(3L − s)v，解出 v = \(\frac{U}{{B(3L - s)}}\)，v 随位移 s 的增大而非线性增大，

依据数学原理，A 逐渐增大。故全过程中，A 先不变后增大。

（3）导棒在 d、e 之间运动的过程中，安培力恒定，

W_A1 = −BI·(2L)·s₁ = − B(\(\frac{U}{R}\))·(2L)·L = − \(\frac{{2BU{L^2}}}{R}\)；

此后的过程中，I = \(\frac{U}{R}\) 恒定，安培力 F_A = BI·(3L − s) = \(\frac{BU}{R}\)·(3L − s) 随位移 s 的增大，由 \(\frac{{2BUL}}{R}\) 线性减小到 \(\frac{{BUL}}{R}\)

故安培力的平均值  \({\bar F_A}\) = \(\frac{{3BUL}}{2R}\)，

此阶段，安培力做功W_A2 = − \({\bar F_A}\)·s₂ = − \({\bar F_A}\)·L = − \(\frac{{3BU{L^2}}}{{2R}}\)。

全过程，安培力做功 W_A = W_A1 + W_A2 = − \(\frac{{7BU{L^2}}}{{2R}}\)