1．静电可通过物体间的__________、_________、_______等方式来产生。这些起电方式的本质都源于物质的原子中的___________在不同物体间或者同一物体的不同部分间发生转移。

【答案】

摩擦，接触，感应，电子

 

2．将不带电的导体 A 和带有负电荷的导体 B 接触后，导体 A 中的电子数________，质子数________（选填“增加”、“减少”或“不变”）。

【答案】

增加，不变

【解析】

物体接触带电时电子发生转移，导体 B 的多余电子转移到了不带电的导体 A，从而使导体 A 带负电，而并非质子数目的变化，质子数目在接触过程中是不变的。

 

3．一个负二价硫离子所带电荷量为________C。一个原来不带电的物体经接触后，所带的电荷量为 + 8 × 10⁻⁸ C，该物体__________（选填“得到”或“失去”）__________个电子。

【答案】

− 3.2 × 10⁻¹⁹，失去，5 × 10¹¹

 

4．在环境的温度、湿度、气压相同的情况下，玻璃、尼龙、羊毛、丝绸、棉花、纸张、硬橡胶、腈纶……中的两种物质摩擦时，排在前面的物质带正电，后面的物质带负电，而且两种物质在上述序列中距离越远，摩擦起电现象越显著。用事先准备的尼龙、丝绸、腈纶三种材料进行摩擦起电的实验：尼龙棒与丝绸摩擦后，尼龙棒带_______（选填“正”或“负”）电；腈纶与丝绸摩擦，腈纶带____（选填“正”或“负”）电；将这三种材料中的_________与__________摩擦，会有更显著的起电现象。

【答案】

正，负，尼龙（腈纶），腈纶（尼龙）

【解析】

两个物体相互摩擦，哪个物体带正电，哪个物体带负电，主要决定于物质失去电子的难易程度。因为在序列中，尼龙在前，丝绸居中，腈纶最后，所以尼龙与丝绸摩擦，尼龙带正电；丝绸与腈纶摩擦，腈纶带负电。尼龙与腈纶摩擦，起电现象最显著。4

 

5．如图所示，导体 AB 靠近带正电的小球 Q 放置，则：（1）若用手接触 B 端，移去手指再移去带正电的小球 Q，导体 AB 是否带电？若带电，带何种电荷？（2）若用手接触 A 端，移去手指再移去带正电的小球 Q，导体 AB 是否带电？若带电，带何种电荷？简述理由。

【答案】

（1）导体 AB 带电，带负电荷

（2）导体 AB 带电，带负电荷

导体 AB 在带正电的小球 Q 附近时，导体棒上的自由电子会向导体棒的左边运动，导体棒的左端因有了多余的电子而带负电，右端因失去电子而带正电。而当手碰在导体棒上，不论是 A 端还是 B 端时，导体棒通过人体与大地相连而成为一大导体；导体棒成为距 Q 较近的近端，带负电。移去手指再移去 Q 后，导体棒仍带负电。

 

6．研究表明，0.3 A 的电流通过人的胸部会使心脏颤动，这将破坏正常的心跳节奏，干扰血液循环和血氧供应。如果电流持续 2 min，则有多少电子通过胸部？

【答案】

2.25 × 10²⁰ 个电子

【解析】

q = It = 0.3 × 2 × 60 C = 36 C

n = \(\frac{q}{e}\) = \(\frac{{36}}{{1.6 \times {{10}^{ - 19}}}}\) = 2.25 × 10²⁰ 个

 

7．某实验室备有以下器材：塑料直尺、塑料三角尺、塑料笔杆、木质梳子、玻璃棒、毛皮、橡胶棒、丝绸、尼龙布、纱布、由细线悬挂的泡沫塑料球。能否选用已有器材设计一个实验以确定用尼龙布摩擦过的塑料直尺带的是正电还是负电？若能，试写出所需器材和主要实验步骤。

【答案】

所需器材：由细线悬挂的泡沫塑料球、塑料直尺、尼龙布、玻璃棒和丝绸（或橡胶棒和毛皮）。

主要实验步骤：先用丝绸摩擦玻璃棒（毛皮摩擦橡胶棒），使玻璃棒带正电（负电），再让玻璃棒（橡胶棒）接触由细线悬挂的泡沫塑料球，使小球也带正电（负电），再把用尼龙布摩擦过的塑料直尺靠近小球。如果是排斥的，塑料直尺就带正电（负电）；如果是吸引的，塑料直尺带的就是负电（正电）。

 

8．在物理学中，为了研究问题的方便，有时需要突出问题的主要方面，忽略次要因素，例如，将带电体抽象为点电荷。把带电体看成点电荷的条件是_________________________，点电荷概念的提出采用了___________的科学研究方法。

【答案】

带电体的大小、形状、电荷分布对它们之间的相互作用的影响可忽略；理想化模型（物理模型、模型建构）

 

9．静电力常量是 k = 9 × 10⁹ _______，其物理意义是：两个均带_________C 电荷量的点电荷，相距________m 时，它们相互间的库仑力大小是_________N。

【答案】

N·m²/C²，1，1，9 × 10⁹

 

10．判断以下说法是否正确，简述理由。

说法	判断	理由（可以举例或推理）
只有体积很小的带电体才能看成点电荷
元电荷的数值最早是由美国物理学家密立根测得的，元电荷是物理学的基本常数之一
由公式 F = k \(\frac{{{q_1}{q_2}}}{{{r^2}}}\)  知，当真空中的两个电荷间的距离 r → 0 时，它们之间的静电力 F → ∞
一带正电的金属小球放在潮湿的空气中，一段时间后发现该小球几乎不带电了。这是因为小球上原有的正电荷会自动逐渐消失

【答案】

错；当带电体的形状、大小及电荷的分布状况对它们之间的作用力影响可以忽略时，可以看成点电荷

对；该说法符合科学史实。

错；当两个电荷距离趋于0时，两电荷不能看成点电荷，此时库仑定律的公式不再适用。

错；小球几乎不带电了，是因为小球上原有多余的正电荷与周围空气中的负离子中和，而不是小球上原有多余的正电荷消失了。

 

11．库仑定律的适用条件是_______________________。有两个相距 10 cm 的点电荷，它们的电荷量分别是 + 4.0 × 10⁻⁹ C和 − 2.0 × 10⁻⁹ C，这两个电荷间的相互作用力大小为__________N，它们之间有__________（选填”吸引”或”排斥”）的相互作用。

【答案】

静止的点电荷，7.2 × 10⁶，吸引

【解析】

F = k \(\frac{{\left| {{q_1}} \right| \cdot \left| {{q_2}} \right|}}{{{r^2}}}\) = 9 × 10⁹ × \(\frac{{4.0 \times {{10}^{ - 9}} \times 2.0 \times {{10}^{ - 9}}}}{{{{0.1}^2}}}\) N = 7.2 × 10⁻⁶ N

 

12．两个完全相同的小金属球（皆可视为点电荷），所带电荷量之比为 7∶3，它们在相距一定距离时相互作用的吸引力为 F₁，如果让它们充分接触后再放回各自原来的位置上，此时相互作用力变为 F₂，则 F₁ 与 F₂ 的大小之比为____________。

【答案】

21∶4

【解析】

设两个相同小金属球所带电荷量分别为 7Q 和 3Q，它们在相距一定距离时相互作用力为 F₁ = k \(\frac{{21{Q^2}}}{{{r^2}}}\)；由于相互吸引，故两金属球带异号电荷。接触后再分开，两球电荷量的绝对值均为 2Q，此时两球的库仑力 F₂ = k \(\frac{{4{Q^2}}}{{{r^2}}}\) = \(\frac{4}{21}\)F₁，则 F₁∶F₂ 大小之比为 21∶4。

 

13．将电荷量为 + 8 × 10⁻⁸ C 的带电小球分成两部分（带电小球的大小可忽略），两部分相距 4 cm。求这两部分之间的静电力大小的最大值。

【答案】

9 × 10⁻³ N

【解析】

设两部分电荷量分别为 q₁ 和 q₂，由于 q₁ + q₂ = 恒量，根据基本不等式 ab ≤ （\(\frac{{a + b}}{2}\)）²，当且仅当 a = b 时等号成立，所以当 q₁ = q₂ = + 4 × 10⁻⁸ C 时静电力最大。

F = k \(\frac{{{q_1}{q_2}}}{{{r^2}}}\) = 9 × 10⁹ × \(\frac{{{{(4.0 \times {{10}^{ - 8}})}^2}}}{{{{0.04}^2}}}\) = 9 × 10⁻³ N

 

14．两个电荷量相等的带电体间保持 3.2 × 10⁻³ m 的距离，由静止开始释放。假设这两个带电体仅受相互间的库仑力作用。释放瞬间第一个带电体获得 7 m/s² 的加速度，第二个带电体获得 9 m/s² 的加速度。若第一个带电体的质量为 6.3 × 10⁻⁷ kg，第二个带电体的质量为多大？每个带电体的电荷量是多少？

【答案】

4.9 × 10⁻⁷ kg，7.08 × 10⁻¹¹ C

【解析】

两带电体间静电力大小相等、方向相反、作用在同一直线上。

F₁ = F₂

m₁a₁ = m₂a₂

m₂ = \(\frac{{{a_1}}}{{{a_2}}}\) m₁ = \(\frac{7}{9}\) × 6.3 × 10⁻⁷ kg = 4.9 × 10⁻⁷ kg

F₁ = k \(\frac{{q^2}}{{{r^2}}}\)

q = \(\sqrt {\frac{{F{r^2}}}{k}} \) = \(\sqrt {\frac{{{m_1}{a_1}{r^2}}}{k}} \) = \(\sqrt {\frac{{6.3 \times {{10}^{ - 7}} \times 7 \times {{(3.2 \times {{10}^{ - 3}})}^2}}}{{9.0 \times {{10}^9}}}} \) C ≈ 7.08 × 10⁻¹¹ C

 

15．如图所示，水平轴上有两个质子（符号 p）和一个电子（符号 e），中心质子处在电子与另一质子连线的中点，求：

（1）中心质子受到左侧电子相互作用而产生的静电力的方向；

（2）中心质子受到右侧质子相互作用而产生的静电力的方向；

（3）中心质子受到的合力的方向。

【答案】

（1）水平向左

（2）水平向左

（3）水平向左

 

16．如图所示，三个电荷量分别为 + q 或 – q 的点电荷固定在坐标轴上。在所有的四种情况中，各点电荷到坐标原点的距离都相等，则 y 轴上电荷所受到的静电力合力的方向为何？

【答案】

各图中 y 轴上电荷所受到的静电力合力的方向依次为：

y 轴负方向（竖直向下），y 轴负方向（竖直向下），x 轴正方向（水平向右），x 轴负方向（水平向左）

 

17．电荷之间的相互作用是通过___________发生的。电场的基本性质是对放入其中的电荷有_________的作用。放入电场中某点的电荷所受的__________和其_________之比叫做该点的电场强度，物理学中规定电场中某点的电场强度方向跟______电荷在该点所受电场力的方向相同。

【答案】

电场，力，电场力，电荷量，正

 

18．如图为某区域的电场线，A、B、C 为电场中的三点，在图中分别画出放在 A、B 两点处的正、负电荷所受电场力的方向和 C 点处的电场强度方向。

【答案】

如图所示

 

19．如图所示，在电荷量为 Q 的点电荷产生的电场中，电荷量为 q 的负试探电荷在 A 点受到的电场力为 F，方向水平向左。A 点的电场强度的大小和方向为何？

【答案】

F/q，方向水平向右

 

20．在如图所示的电场中，一电荷量为 − 1.0 × 10⁻⁸ C 的试探电荷在 A 点所受电场力大小 F = 2.0 × 10⁻⁴ N，则 A 点的电场强度的大小 E = ________N/C，方向为_______（选填“向左”或“向右”；该试探电荷所受电场力 F 的方向为_________（选填”向左”或”向右”）。若取走试探电荷，则 A 点的电场强度的大小 E = _________N/C。

【答案】

 2.0 × 10⁴，向右，向左，2.0 × 10⁴

【解析】

A 点电场强度的大小为：E = \(\frac{F}{q}\) = \(\frac{{2.0 \times {{10}^{ - 4}}}}{{1.0 \times {{10}^{ - 8}}}}\) N/C = 2.0 × 10⁴ N/C，方向向右。根据负试探电荷受力方向和电场方向相反可得：试探电荷在 A 点所受电场力的方向向左，若取走试探电荷，则 A 处的电场强度仍为 2.0 × 10⁴ N/C。

 

21．在匀强电场中发射 a、b、c、d、e 五个质子，每个质子的发射速度大小和方向如图所示。问：这五个质子在电场中的加速度大小关系如何？

【答案】

加速度大小都相等

【解析】

a = \(\frac{F}{m}\) = \(\frac{qE}{m}\) = \(\frac{q}{m}\) E，匀强电场中各处的电场强度 E 相同，质子的荷质比 \(\frac{q}{m}\) 又是一定的，与质子的速度无关，所以加速度的大小都相等。

 

22．带电粒子在距离其 50 cm 处产生的电场强度的大小为 0.3 N/C。求带电粒子电荷量的大小。

【答案】

8.33 × 10⁻¹² C

【解析】

E = k \(\frac{q}{{{r^2}}}\)

q = \(\frac{{E{r^2}}}{k}\) = \(\frac{{0.3 \times {{(0.5)}^2}}}{{9 \times {{10}^9}}}\) C ≈ 8.33 × 10⁻¹² C

 

23．库仑通过和万有引力的类比得出了电荷间作用力跟距离的二次方成反比的规律。有质量的物体周围存在着引力场。如用定义静电场电场强度的方法来定义引力场的场强，类比可得，与质量为 M 的质点相距 r 处的引力场场强的表达式为 E_G = __________（万有引力恒量用 G 表示）。

【答案】

\(\frac{{GM}}{{{r^2}}}\)

 

24．如图所示，用两根绝缘线把两个电荷量的大小均为 q 的带电小球悬挂起来，a 球带正电荷，b 球带负电荷。设两球间的库仑力小于 b 球的重力。现加一水平向左的匀强电场，画出两小球处于平衡状态时两小球的大致位置，简述理由。

【答案】

如图所示，以两个小球整体为研究对象，可判断 a 球上方绝缘线处于竖直绷紧状态。再以 b 球为研究对象，根据平衡条件可判断 a 与 b 之间绝缘线向右偏转。

 

25．如图所示，用一根绝缘细线悬挂一个带电小球，小球的质量为 1.0 × 10⁻² kg，所带的电荷量为 + 2.0 × 10⁻⁸ C。现加一水平向右的匀强电场，平衡时绝缘细线与竖直方向成 30° 角，则：（1）该匀强电场的电场强度为多大？（2）若改变所加电场的方向，使小球在图中位置仍保持平衡，所加的最小电场的电场强度大小为多大？方向如何？

【答案】

（1）E ≈ 2.9 × 10⁶ N/C

（2）E_min = 2.5 × 10⁶ N/C

【解析】

（1）qE = mgtan30°

E = \(\frac{{mg\tan 30^\circ }}{q}\) = \(\frac{{1.0 \times {{10}^{ - 2}} \times 10 \times \frac{{\sqrt 3 }}{3}}}{{2.0 \times {{10}^{ - 8}}}}\) N/C ≈ 2.9 × 10⁶ N/C

（2）qE_min = mgsin30°

E_min = \(\frac{{mg\sin 30^\circ }}{q}\) = \(\frac{{1.0 \times {{10}^{ - 2}} \times 10 \times 0.5}}{{2.0 \times {{10}^{ - 8}}}}\) N/C = 2.5 × 10⁶ N/C

由于点到直线的距离以垂线（到垂足）最短，电场强度 E 沿此方向数值最小，故最小电场强度的方向为垂直细线向上

 

26．四个带电粒子间隔均匀地分布于 O 点的左右两侧，带电粒子的电荷量如图所示。根据各图中 O 点处电场强度的大小，按由大到小的顺序进行排序。

【答案】

E₂ > E₄ > E₃ > E₁

【解析】

根据对称性可知，关于中心点对称的两点电荷合电场强度为零，所以 E₁ = 0。根据点电荷电场强度 E = k \(\frac{q}{{{r^2}}}\) 和电场强度的叠加原理可得到：

E₂ = k \(\frac{e}{{{{(2d)}^2}}}\) + k \(\frac{e}{{{{(2d)}^2}}}\) + k \(\frac{e}{{{d^2}}}\) + k \(\frac{e}{{{d^2}}}\) = \(\frac{5}{2}\) k \(\frac{e}{{{d^2}}}\)，方向向右

E₃ = k \(\frac{e}{{{{(2d)}^2}}}\) + k \(\frac{e}{{{{(2d)}^2}}}\) = \(\frac{1}{2}\) k \(\frac{e}{{{d^2}}}\)，方向向左

E₄ = k \(\frac{e}{{{d^2}}}\) + k \(\frac{e}{{{d^2}}}\) = 2k \(\frac{e}{{{d^2}}}\)，方向向左

所以，中心点处电场强度的大小按由大到小排序：E₂ > E₄ > E₃ > E₁

 

27．静电场是___________周围空间存在的一种物质；通常用_______来描述电场力的性质，用_________来描述电场能量的性质。正电荷沿着电场线运动，电势________，电势能________。

【答案】

静止电荷，电场强度，电势，降低，减小

 

28．在电场中电场力对其中移动的电荷做功与__________无关，只决定于__________。电场力做正功，电势能___________；克服电场力做功，电势能________。电场力对电荷做功与电荷的电势能的变化量的关系为_________。

【答案】

路径，始、末位置，减小，增加，W = − ΔE_p

 

29．判断以下关于电势和电势能的说法是否正确，简述理由。

说法	判断	理由（可以举例或推理）
电荷在电场中电势高的地方，具有较大的电势能
具有较大的电荷量的电荷，有较大的电势能
负电荷具有的电势能可以比正电荷具有的电势能大
只有当电荷有较大的电荷量，又在电势较高的地方，它才具有较大的电势能

【答案】

错。负电荷在电势高的地方，具有的电势能较小。

错。E_p = qφ 电势能除了与电荷量有关还与所处位置的电势有关（如零电势）。

对。电势能除与电荷的正、负有关外，还同电势有关。例如负电荷在负电势处的电势能（大于 0）就比正电荷在负电势处的电势能（小于 0）大。

错。例如负电荷有较大的电荷量，又在电势为正且较高的地方，电势能反而较小。

 

30．将一电荷量为 q = + 2.0 × 10⁻⁶ C的点电荷从无穷远处移至电场中的 A 点，电场力做了 4.0 × 10⁻⁵ J 的功，则 A 点的电势为多少？

【答案】

− 20 V

【解析】

设无穷远处电势为零。从无穷远处到 A，电场力做正功 W = 4.0 × 10⁻⁵ J，等效于从 A 到无穷远处，电场力做负功 W = − 4.0 × 10⁵ J，即正电荷在 A 点的电势能为 E_p = − 4.0 × 10⁻⁵ J。

φ_A = \(\frac{{{E_p}}}{q}\) = \(\frac{{ - 4.0 \times {{10}^{ - 5}}}}{{2.0 \times {{10}^{ - 6}}}}\) V = − 20 V

 

31．电场中有 A、B 两点，A 点的电势比 B 点的高，A 点电势为零。一个点电荷 q 被先后放在 A 点和 B 点，当该电荷从 A 点移动到 B 点时，是电场力做功还是克服电场力做功？点电荷放在哪一点时其电势能较大？

【答案】

若点电荷 q 为正电荷，则由于 A 点的电势比 B 点的高，说明电荷 q 在 A 点的电势能大于在 B 点的电势能；从 A 点移到 B 点，电势能减少，电场力做正功。

若点电荷 q 为负电荷，则由于 A 点的电势比 B 点的高，说明负电荷在 A 点的电势能小于在 B 点的电势能；从 A 点移到 B 点，电势能增加，电荷克服电场力做功。

 

32．甲同学认为“电场强度大的地方电势一定高，例如孤立正电荷周围靠近正电荷处”，乙同学认为“电场强度为零的地方电势一定为零，例如无穷远处”，丙同学则认为“电势相等处电场强度也一定相等，例如匀强电场的等势面处”。你是否同意他们的说法？简述理由。

【答案】

他们三位同学的说法都不正确，电场强度的大小与电势的高低没有关系。

 

33．如图（a）所示，A、B 为一条电场线上的两点。将一正电荷由 A 点静止释放，正电荷仅在电场力的作用下向 B 点运动，运动过程的速度 – 时间图像如图（b）所示。比较正电荷分别在 A、B 两点的电场强度大小与电势高低，简述理由。

【答案】

正电荷仅在电场力的作用下由 A 点向 B 点运动，速度增加，动能增大，电势能减小。正电荷的电势能 E_pA > E_pB，所以 φ_A > φ_B。v – t 图斜率表示加速度，由图可得斜率变大，所以 a_A < a_B，因为 a = \(\frac{q}{m}\)E，所以 E_A < E_B。

 

34．如图所示，处于真空中的立方体中心或顶角处存在电荷量为 + q 或 − q 的点电荷。以下四种情况中，a、b 两点的电场强度和电势均相同的是（    ）。

【答案】

D

【解析】

根据点电荷的电场强度公式 E = k \(\frac{q}{{{r^2}}}\)，可求得各个点电荷分别在 a、b 两点产生的电场强度，再根据矢量的合成，可得 a、b 两点的电场强度大小和方向。再根据几种常见电场的等势面分布情况可判断 a、b 两点的电势关系，故 D 正确。

 

35．下列基本概念与规律中既适用于点电荷产生的静电场也适用于匀强电场的是（    ）。

① 电场强度 E = \(\frac{F}{q}\)           ② 电场强度 E = \(\frac{U}{d}\)          ③ 电场强度 E = k \(\frac{q}{{{r^2}}}\)        ④ 电势差 U_AB = \(\frac{{{W_{AB}}}}{q}\)

A．①③        B．②③        C．②④        D．①④

【答案】

D

 

36．电子伏（eV）与 SI 制的能量单位焦耳（J）的换算关系为 1 eV = _________J。 

【答案】

1.6 × 10⁻¹⁹

 

37．将一带电粒子从电势为 2 000 V 的 A 点移动到电势为 3 600 V 的 B 点，电场力做功 3.2 × 10⁻⁶ J，求这一带电粒子的电荷量。

【答案】

− 2.0 × 10⁻⁹ C

【解析】

U_AB = φ_A − φ_A =（2 000 − 3 600）V = − 1.6 × 10³ V

q = \(\frac{{{W_{AB}}}}{{{U_{AB}}}}\) = \(\frac{{3.2 \times {{10}^{ - 6}}}}{{ - 1.6 \times {{10}^3}}}\) C = − 2.0 × 10⁻⁹ C

 

38．电场线分布如图所示，电场中 a、b 两点的电场强度大小分别为 E_a 和 E_b 电势分别为 φ_a 和 φ_b，比较 a、b 两点的电场强度大小与电势高低。

【答案】

E_a < E_b，φ_a > φ_b

【解析】

可根据电场线的疏密判断电场强度的大小；绘制 a、b 两点所处的等势面和电场线的方向判断 a、b 两点的电势高低。

 

39．如图所示，水平实线表示匀强电场的电场线（箭头未画出）。一个带正电荷的粒子以某一速度射入该电场，仅在电场力作用下的运动轨迹如图中的虚线所示，a、b 为轨迹上的两点，则匀强电场的电场强度方向为_________。若 a 点的电势为 φ_a，b 点的电势为 φ_b。，则 φ_a __________（选填“>”“=”或“<”）φ_b。

【答案】

水平向右，>

 

40．如图所示，水平实线表示匀强电场的电场线（箭头未画出）。电场中有 A、B 两点，AB = 4 cm。将一电荷量为 + 1.0 × 10⁻⁶ C的点电荷放在 A 点时，电势能为 4.0 × 10⁻⁴ J。将一电荷量为 − 2.0 × 10⁻⁷ C 的点电荷放在 B 点时，电势能为 5.0 × 10⁻⁶ J，则 A、B 两点的电势差 U_AB 为________V，电场强度 E 的大小为_______N/C，方向为_________。

【答案】

425，2.125 × 10⁴，水平向右

【解析】

φ_A = \(\frac{{{E_{pA}}}}{q}\) = \(\frac{{4.0 \times {{10}^{ - 4}}}}{{  1.0 \times {{10}^{ - 6}}}}\) V = 400 V

φ_B = \(\frac{{{E_{pB}}}}{q}\) = \(\frac{{5.0 \times {{10}^{ - 6}}}}{{  - 2.0 \times {{10}^{ - 7}}}}\) V = −25 V

U_AB = φ_A − φ_B = 400 −（− 25）V = 425 V

E = \(\frac{{{U_{AB}}}}{d}\) = \(\frac{{{U_{AB}}}}{{AB \cdot \cos 60^\circ }}\) = \(\frac{{425}}{{0.04 \times 0.5}}\) V/m = 2.125 × 10⁴ N/C

因为沿电场线电势降低且 φ_A > φ_B，所以电场强度方向水平向右

 

41．图（a）、（b）、（c）为匀强电场中的三组垂直于纸面的等势面，三张图的比例尺相同，则：（1）图（a）、（b）、（c）所示区域内电场强度的大小关系如何？（2）哪组电场强度的方向是竖直向下的？

【答案】

（1）E_a > E_b = E_c。

（2）图（c）所示的电场强度的方向竖直向下。

【解析】

（1）因为 E = \(\frac{U}{d}\)，且三组等势面上、下间距离 d 均相同，所以比较电势差的大小即可得到电场强度的大小。由图像可得相同间距的上、下两等势面间电势差的大小：U_a = 80 V；U_b = 40 V；U_c = − 40 V。可得 E_a > E_b = E_c。

（2）电势沿电场线逐渐降低。若电场强度的方向竖直向下，则由上而下电势下降，因此图（c）所示的电场强度的方向竖直向下。

 

42．在匀强电场中一组竖直方向的等势面如图所示，则匀强电场的方向如何？若将电子沿图中五条路径从一个等势面移动到另一个等势面，对于每条路径，移动前后两点间的电势差是多少？沿每条路径电场力对电子做多少功？

【答案】

 水平向右（与等势面垂直）

五条路径的电势差分别为 U₁ = U₂ = 10 V，U₃ =  20 V，U₄ = − 10 V，U₅ =  10 V。

W₁ = W₂ = W₅ = − 1.6 × 10⁻¹⁸ J，W₃ = − 3. 2 × 10⁻¹⁸ J，W₄ = 1.6 × 10⁻¹⁸ J

【解析】

五条路径的电势差分别为 U₁ = U₂ = 80 V − 70 V = 10 V，U₃ = 80 V − 60 V = 20 V，U₄ = 60 V − 70 V = − 10 V，U₅ = 70 V − 60 V = 10 V。

根据 W_AB = eU_AB

W₁ = W₂ = W₅ = eU₁ = （− 1.6 × 10⁻¹⁹）× 10 J = − 1.6 × 10⁻¹⁸ J

W₃ = eU₃ = （− 1.6 × 10⁻¹⁹） × 20 J = − 3. 2 × 10⁻¹⁸ J

W₄ = eU₄ = （− 1.6 × 10⁻¹⁹） × （− 10）J = 1.6 × 10⁻¹⁸ J

 

43．如图所示，在电场中有 A、B、C 三点分别处于两个不同的等势面上，若将一个电子从 A 移至 B，电场力做功 6.4 × 10⁻¹⁸ J，求电势差 U_BA、U_AC、U_CB。

【答案】

U_BA = 40 V，U_AC = − 40 V，U_CB = 0

【解析】

U_AB = \(\frac{{{W_{AB}}}}{q}\) = \(\frac{{6.4 \times {{10}^{ - 18}}}}{{ - 1.6 \times {{10}^{ - 19}}}}\) V = − 40 V

U_BA = − U_AB = 40 V

U_AC = U_AB = − 40 V

因为 B 与 C 在同一等势面上，所以 U_CB = 0。

 

44．如图所示，一个电子由 A 点静止释放，仅在电场力的作用下加速通过 B 点。A 点和 B 点间电势差的大小为 100 V。试问：

（1）A、B 两点的电势哪个高？

（2）电子在 B 点处的动能为多大？

【答案】

（1）B 点电势高

（2）E_kB = 100 eV

【解析】

（1）电子静止释放仅在电场力的作用下加速运动，说明电场力做正功 W_AB

U_AB = \(\frac{{{W_{AB}}}}{q}\) = \(\frac{{{W_{AB}}}}{e}\)，因为 W_AB > 0，e < 0（？？这样表述不太好吧），所以 U_AB < 0 即 φ_A < φ_B。

故 B 点电势高

（2）U_AB = − 100 V

电子在仅有电场力做功 W_AB = eU_AB 的情况下加速运动，则根据动能定理有：

eU_AB = E_kB – 0

E_kB = （− 1.6 × 10⁻¹⁹）×（− 100）J = 1.6 × 10⁻¹⁷ J = 100 eV

 

45．上海市质子重离子医院（SPHIC）是我国首家同时拥有质子和重离子放射治疗技术的医疗机构。医院使用直线加速器（图 9 – 20）将质子由静止预加速到 7 MeV 的能量，之后再将质子注入同步加速器进行加速，速度达到光速的 70% 时被引入治疗室，能够治疗人体内 30 cm 深度的肿瘤。试问：

（1）质子经直线加速器预加速后获得的速度大小是多少？

（2）如果在直线加速器的匀强电场中加速长度为 3 m，则加速匀强电场的电场强度为多大？（质子的质量为 1.67 × 10⁻²⁷ kg）

【答案】

（1）v ≈ 3.66 × 10⁷ m/s

（2）E ≈ 2.33 × 10⁶ N/C

【解析】

（1）W = \(\frac{1}{2}\)mv²

v = \(\sqrt {\frac{{2W}}{m}} \) = \(\sqrt {\frac{{2 \times 7 \times {{10}^6} \times 1.6 \times {{10}^{ - 19}}}}{{1.67 \times {{10}^{ - 27}}}}} \) m/s ≈ 3.66 × 10⁷ m/s

（2）qEd = \(\frac{1}{2}\)mv²

E = \(\frac{W}{{qd}}\) = \(\frac{{7 \times {{10}^6} \times 1.6 \times {{10}^{ - 19}}}}{{1.6 \times {{10}^{ - 19}} \times 3}}\) N/C ≈ 2.33 × 10⁶ N/C

 

46．关于电容器，下列说法中正确的是（    ）。

A．电容器所带电荷量与两极板间的电势差成反比

B．电容器两极板间的电势差越高，电容就越大

C．电容器所带的电荷量越多，电容就越大

D．电容是描述电容器储存电荷本领的物理量

【答案】

D

 

47．一平行板电容器充电完成后两板间电势差为 16 V，极板所带的电荷量为 7.52 × 10⁻³ C，则此电容器的电容为 _______ μF；再对电容器放电，放电结束后电容器的电容为 _______μF。

【答案】

470，470

【解析】

平行板电容器的电容 C = \(\frac{Q}{U}\) = \(\frac{{7.52 \times {{10}^{ - 3}}}}{{16}}\) F = 4.7 × 10⁻⁴ F = 470 μF；电容反映电容器本身的特性，电容器不带电时电容不变，仍为 470 μF。

 

48．超级电容器是一种专门用于储能的特种电容器，在工业、电子产品、医疗、交通运输和军事等方面都有应用。如图所示，一超级电容器标有“2.7 V 100 F”，将该电容器接在 1.5 V 干电池的两端，求充电完成后该电容器所带的电荷量。

【答案】

150 C

【解析】

实际电压 1.5 V 低于电容器的额定电压 2.7 V，所以充电完成时电容器两极板间电势差为 1.5 V。根据 C = \(\frac{Q}{U}\) 可得，电容器所带的电荷量为 Q = CU = 100 × 1.5 C = 150 C。

 

49．一个电容器所带的电荷量为 4 × 10⁻⁸ C，两极板间的电势差为 10 V。

（1）求这个电容器的电容。

（2）如果电容器的电荷量减少了 1×10⁻⁸ C，则两极板间的电压为多大？

【答案】

（1）C = 4 × 10⁻⁹ F

（2）U′ =7.5 V

【解析】

（1）C = \(\frac{Q}{U}\) = \(\frac{{4 \times {{10}^{ - 8}}}}{{10}}\) F = 4 × 10⁻⁹ F。

（2）电荷量减小后，电荷量为 3 × 10⁸ C，电容不变，故电压 U′ = \(\frac{{Q'}}{U}\) = \(\frac{{4 \times {{10}^{ - 8}} - 1 \times {{10}^{ - 8}}}}{{4 \times {{10}^{ - 9}}}}\) V = 7.5 V。

 

50．如图所示，金属平行板电容器的电容为 100 pF，两极板 A、B 之间相距 1 cm，电源电压为 60 V。对电容器充电，当两板间的电势差增大至与电源电压相等时，求：

（1）电容器间的匀强电场的电场强度的大小和方向；

（2）电容器所带的电荷量。

【答案】

（1）E = 6 × 10³ N/C。场强方向由 A 板指向 B 板。

（2）Q = 6 × 10⁻⁹ C

【解析】

（1）电容器间的匀强电场的电场强度大小：E = \(\frac{U}{d}\) = \(\frac{{60}}{{1 \times {{10}^{ - 2}}}}\) V/m = 6 × 10³ N/C。

A 板带正电，B 板带负电，所以场强方向由 A 板指向 B 板。

（2）电容器所带的电荷量 Q = CU = 100 × 10⁻¹² × 60 C = 6 × 10⁻⁹ C。

 

51．用如图所示电路给电容器进行充、放电。若通过图中电流表的电流方向向右，那么电路中电流表的示数变化是 ________（选填“增大”或“减小”），单刀双掷开关 S 当前接通________（选填“1”或“2”）位置，电容器两端的电压表的示数变化是__________（选填“增大”或“减小”），电容器此时处于___________（选填“充电”或“放电”）状态。若通过图中电流表的电流方向向左，那么电路中电流表的示数变化是__________（选填“增大””或“减小”），单刀双掷开关 S 当前接通_______（选填“1”或“2”）位置，电容器两端的电压表的示数变化是__________（选填“增大”或“减小”），电容器此时处于_________（选填“充电”或“放电”）状态。

【答案】

减小，1，增大，充电，减小，2，减小，放电

 

52．电容器在充电和放电过程中，整个电路中能量是如何转化的？

【答案】

在电容器充电过程中，电源的电能转化为电容器储存的电场能和整个电路的内能（电热）；在电容器放电过程中，电容器储存的电场能转化为整个电路的内能（电热）。

 

53．如图所示，平行板电容器两极板间有电场强度为 E 的匀强电场，且带正电的极板接地，以正电极板为坐标原点沿电场方向建立如图所示的坐标轴。一质量为 m，电荷量为 + q 的带电粒子（不计重力）从 x 轴上坐标为 x₀ 处静止释放。

（1）求该粒子在 x₀ 处的电势能。

（2）试运用牛顿第二定律证明，该带电粒子在两极板间运动的过程中，动能与电势能之和保持不变。

【答案】

（1）带正电的极板接地作为零势能面，若带电粒子从正极板到 x₀ 处电场力做功为

W = qEx₀                                           ①

W = − ΔE_p = −（E_p − 0）                    ②

由 ①、② 式可得：E_p = − qEx₀

（2）在带电粒子的运动方向上任取一点，设坐标为 x，由牛顿第二定律可得：

qE = ma                                            ③

由运动学公式可得：

v² = 2a（x − x₀）                               ④

由 ③、④ 式可得坐标为 x 处：

E_kx = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) \(\frac{{qE}}{a}\) 2a（x – x₀）= qE（x − x₀）

E_p = − qEx

E = E_k + E_p = qE（x – x₀）+（− qEx）= − qEx₀（恒量）

即动能与电势能之和保持不变

 

54．图中属于防范静电危害的是（    ）。

【答案】

D

 

55．静电复印机的基本工作原理是：先使硒鼓带正电，并利用光学方法将原稿上的字迹成像在硒鼓上，留下带_______电的静电潜像，再靠静电的吸引力吸附带______电的墨粉。然后用带______电的白纸与硒鼓接触，吸引硒鼓上的墨粉，最后加热使墨粉熔化留在纸上。

【答案】

正，负，正.2

 

56．根据你的生活经验和学习过的实例，说出如何防范静电对人类的危害？简述静电防范的原理。

【答案】

可采用良好接地、工艺控制、维持适当的空气湿度、使用避雷针（接闪杆）等途径来防范静电的危害。静电防范是让产生的电荷及时传导离开，不产生积累。

 

57．在生产和社会生活中，静电利用是利用电荷间的____________。___________、______________、______________等是利用静电的例子。

【答案】

相互作用，静电除尘，静电喷雾，静电复印

 

58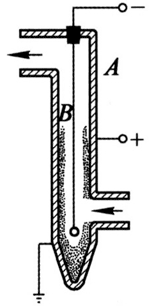．以煤作燃料的工厂、电站，每天排出的烟气里含有大量的煤粉，不仅浪费燃料，而且严重地污染环境。图 9 – 26 是静电除尘器的原理示意图。除尘器由金属管 A 和悬在管中的金属丝 B 组成，A 接到高压电源的正极，B 接到高压电源的负极。简述静电除尘的原理。

【答案】

由于金属管 A 接高压电源的正极，B 接高压电源的负极，在它们之间形成很强的电场；B 附近的空气分子被强电场电离，成为正离子和电子。正离子被吸引到负极 B 上，获得电子后又成为分子；而电子在向正极 A 运动的过程中遇到烟气中的煤粉，使其带负电，在电场力作用下煤粉被吸附到正极 A 上；煤粉堆积到一定程度，受重力作用落在下面的集尘装置中。