1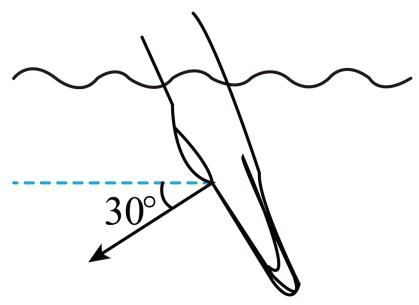．如图所示，人游泳时若某时刻手掌对水的作用力大小为 F，该力与水平方向的夹角为30°，则该力在水平方向的分力大小为

A．2F           B．\(\sqrt 3 \)F              C．F             D．\(\frac{{\sqrt 3 }}{2}\)F

【答案】

D

【解析】

沿水平方向和竖直方向将手掌对水的作用力分解，则有该力在水平方向的分力大小为 Fcos30° = \(\frac{{\sqrt 3 }}{2}\)F，选项D正确。

 

2．放射性元素 ¹²³I 会衰变为稳定的 ¹²³Te，半衰期约为 13 h，可以用于检测人体的甲状腺对碘的吸收。若某时刻 ¹²³I 与 ¹²³Te 的原子数量之比为 4∶1，则通过 26 h 后 ¹²³I 与 ¹²³Te 的质量之比

A．1∶2        B．1∶4        C．1∶8        D．1∶16

【答案】

B

【解析】

根据题述，¹²³I 与 ¹²³Te 原子数量之比为 4∶1，则通过 26 h（两个半衰期）后，4 份 ¹²³I 衰变剩余 1 份，生成了 3 份 ¹²³Te 原子，剩余 ¹²³I 与 ¹²³Te 原子数量之比为1∶4，因为 ¹²³I 与 ¹²³Te 原子质量相同，所以通过 26 h（两个半衰期）后，¹²³I 与 ¹²³Te 原子的质量之比为 1∶4，选项B正确。

 

3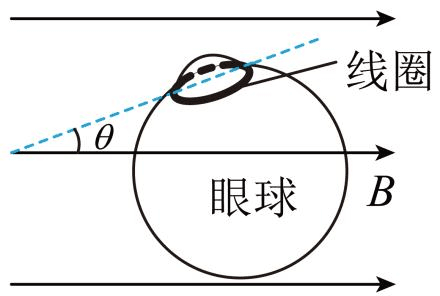．某眼动仪可以根据其微型线圈在磁场中随眼球运动时所产生的电流来追踪眼球的运动。若该眼动仪线圈面积为 S，匝数为 N，处于磁感应强度为 B 的匀强磁场中，线圈平面最初平行于磁场，经过时间 t 后线圈平面逆时针转动至与磁场夹角为 θ 处，则在这段时间内，线圈中产生的平均感应电动势的大小和感应电流的方向（从左往右看）为

A．\(\frac{{NBS\sin \theta }}{t}\)，逆时针                      B．\(\frac{{NBS\cos \theta }}{t}\)，逆时针。

C．\(\frac{{NBS\sin \theta }}{t}\)，顺时针                       D．\(\frac{{NBS\cos \theta }}{t}\)，顺时针。

【答案】

A

【解析】

经过时间 t，面积为 S 的线圈平面逆时针转动至与磁场夹角为 θ 处，磁通量变化ΔΦ = BSsinθ，由法拉第电磁感应定律，线圈中产生的平均感应电动势的大小为 E = N\(\frac{{\Delta \Phi }}{{\Delta t}}\) = \(\frac{{NBS\sin \theta }}{t}\)。由楞次定律可判断出感应电流方向为逆时针方向，选项 A 正确。

 

4．电容式加速度传感器可以用于触发汽车安全气囊等系统。如图所示，极板 M、N 组成的电容器视为平行板电容器，M 固定，N 可左右运动，通过测量电容器极板之间电压的变化来确定汽车的加速度。当汽车减速时，极板 M、N 的距离减小，若极板上电荷量保持不变，则该电容器

A．电容变小

B．极板间电压变大

C．极板间电场强度不变

D．极板间电场强度变小

【答案】

C

【解析】

当汽车减速时，极板 M、N 的距离减小，由平行板电容器的决定式 C = \(\frac{{\varepsilon S}}{{4\pi kd}}\) 可知，电容增大，选项 A 错误；

若极板上电荷量保持不变，由电容定义式 C = Q/U 可知，极板 M、N 之间电压变小，选项B错误；

由于极板上电荷量保持不变，极板正对面积不变，根据电荷产生电场可知，极板之间电场强度不变，选项C正确D错误。

 

5．如图所示。竖直平面内有两个半径为 R，而内壁光滑的 1/4 圆弧轨道，固定在竖直平面内，地面水平，O、O′ 为两圆弧的圆心，两圆弧相切于 N 点。一小物块从左侧圆弧最高处静止释放，当通过 N 点时，速度大小为（重力加速度为 g）

A．\(\sqrt {2gR} \)                   B．\(\frac{{\sqrt {6gR} }}{2}\)

C．\(\frac{{\sqrt {5gR} }}{2}\)                   D．\(\sqrt {gR} \)

【答案】

D

【解析】

由图中几何关系可知，图中 NO 连线与水平方向的夹角 θ = 30°。设小物块通过 N 点时速度为 v，小物块从左侧圆弧最高点静止释放，由机械能守恒定律，mgRsinθ = \(\frac {1}{2} \)mv²，解得：v = (\sqrt {gR} \)，选项 D 正确。

 

6．某电动牙刷的充电装置含有变压器，用正弦交流电给此电动牙刷充电时，原线圈两端的电压为 220 V，副线圈两端的电压为 4.4 V，副线圈的电流为 1.0 A，若将该变压器视为理想变压器，则 

A．原、副线圈匝数之比为 25∶1

B．原线圈的电流为 0.02 A

C．副线圈两端的电压最大值为 5 V

D．原、副线圈的功率之比为 50∶1

【答案】

B

 

7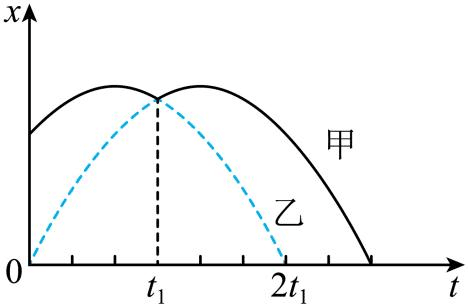．质量相同的甲乙两小球（视为质点）以不同的初速度竖直上抛，某时刻两球发生正碰。题图中实线和虚线分别表示甲乙两球位置随时间变化的曲线，其中虚线关于 t = t₁ 左右对称，实线两个顶点的纵坐标相同，若小球运动中除碰撞外仅受重力，则

A．t = 0 时刻，甲的速率大于乙的速率

B．碰撞前后瞬间，乙的动量不变

C．碰撞前后瞬间，甲的动能不变

D．碰撞后甲的机械能大于乙的机械能

【答案】

C

【解析】

根据位移图像斜率表示速度可知，t = 0 时刻，甲的速率小于乙的速率，选项A错误；

根据甲乙两球位移图像可知，碰撞前后瞬间，两球交换速度，方向反向。根据题述，虚线（乙的位移图像）关于 t = t₁ 左右对称，所以碰撞前后瞬间，乙的动量大小不变，方向变化，甲的动能不变，选项 B 错误 C 正确；

根据题述，实线两个顶点的纵坐标相同，可知碰撞后甲的机械能与乙的机械能相等，选项 D 错误。

 

8．2021 年 5 月 15 日“祝融号”火星车成功着陆火星表面，是我国航天事业发展中具有里程碑意义的进展。此前我国“玉兔二号”月球车首次实现月球背面软着陆，若“祝融号”的质量是“玉兔二号”的 K 倍，火星的质量是月球的 N 倍，火星的半径是月球的 P 倍，火星与月球均视为球体，则

A．火星的平均密度是月球的 \(\frac{N}{{{P^3}}}\) 倍

B．火星的第一宇宙速度是月球的 \(\sqrt {NP} \)

C．火星的重力加速度大小是月球表面的 \(\frac{{\sqrt N }}{P}\)

D．火星对“祝融号”引力大小是月球对“玉兔二号”引力的 \(\frac{{KN}}{{{P^2}}}\) 倍

【答案】

AD

 

9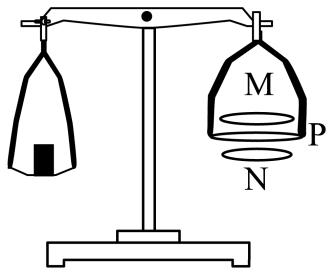．某同学设计了一种天平，其装置如题图所示。两相同的同轴圆线圈 M、N 水平固定，圆线圈 P 与 MN 共轴且平行等距。初始时，线圈 M、N 通以等大反向的电流后，在线圈 P处产生沿半径方向的磁场，线圈 P 内无电流且天平平衡。设从上往下看顺时针方向为正向。当左托盘放入重物后，要使线圈 P 仍在原位置且天平平衡，可能的办法是

A．若 P 处磁场方向沿半径向外，则在 P 中通入正向电流

B．若 P 处磁场方向沿半径向外，则在 P 中通入负向电流

C．若 P 处磁场方向沿半径向内，则在 P 中通入正向电流

D．若 P 处磁场方向沿半径向内，则在 P 中通入负向电流

【答案】

BC

【解析】

当左托盘放入重物后，要使线圈 P 仍在原位置且天平平衡，则需要线圈 P 需要受到竖直向下的安培力。若 P 处磁场方向沿半径向外，由左手定则可知，可在 P 中通入负向电流，选项 A 错误 B 正确；

若P处磁场方向沿半径向内，由左手定则可知，可在 P 中通入正向电流，选项 C 正确 D 错误。

 

10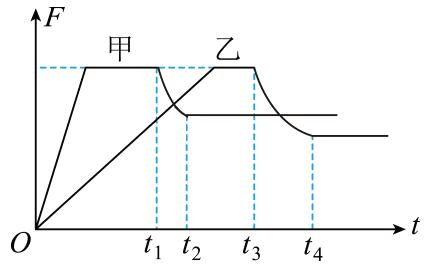．额定功率相同的甲、乙两车在同一水平路面上从静止启动，其发动机的牵引力随时间的变化曲线如题图所示。两车分别从 t₁ 和 t₃ 时刻开始以额定功率行驶，从 t₂ 和 t₄ 时刻开始牵引力均视为不变。若两车行驶时所受的阻力大小与重力成正比，且比例系数相同，则 

A．甲车的总重比乙车大

B．甲车比乙车先开始运动

C．甲车在 t₁ 时刻和乙车在 t₃ 时刻的速率相同

D．甲车在 t₂ 时刻和乙车在 t₄ 时刻的速率相同

【答案】

A

【解析】

根据题述，两车额定功率 P 相同，所受阻力 f = kmg。根据甲车 t₂ 时刻后和乙车 t₄ 时刻后两车牵引力不变时甲车牵引力大于乙车，由 F = f = kmg，可知甲车的总重比乙车大，选项 A 正确；

对甲乙两车启动的第一阶段，牵引力与时间 t 成正比，即 F = k′t，由 k′t = f = kmg，可知不能判断出甲车比乙车先开始运动，选项 B 错误；

t₂ 时刻甲车达到最大速度，t₄ 时刻乙车达到最大速度，根据汽车的额定功率 P = fv_m = kmgv_m，由于甲车的总重比乙车大，所以甲车在 t₂ 时刻的速率小于乙车在 t₄ 时刻的速率，选项 D 错误；

对于牵引力不变阶段，由牛顿第二定律，F − f = ma，做匀变速直线运动，甲车在t₁ 时刻的速率小于乙车在 t₃ 时刻的速率，选项 C 错误。

 

11．某同学用手机和带刻度的玻璃筒等器材研究金属小球在水中竖直下落的速度变化情况。他用手机拍摄功能记录小球在水中静止释放后位置随时间的变化，每 \(\frac{1}{{60}}\) s 拍摄一张照片。

（1）取某张照片中小球的位置为 0 号位置，然后依次每隔 3 张照片标记一次小球的位置，则相邻标记位置之间的时间间隔是_________s。

（2）测得小球位置 x 随时间 t 变化曲线如题图所示，由图可知，小球在 0.15s ~ 0.35 s 时间段平均速度的大小_______（选填“大于”、“等于”、“小于”）在 0.45 s ~0.65 s 时间段内平均速度的大小。

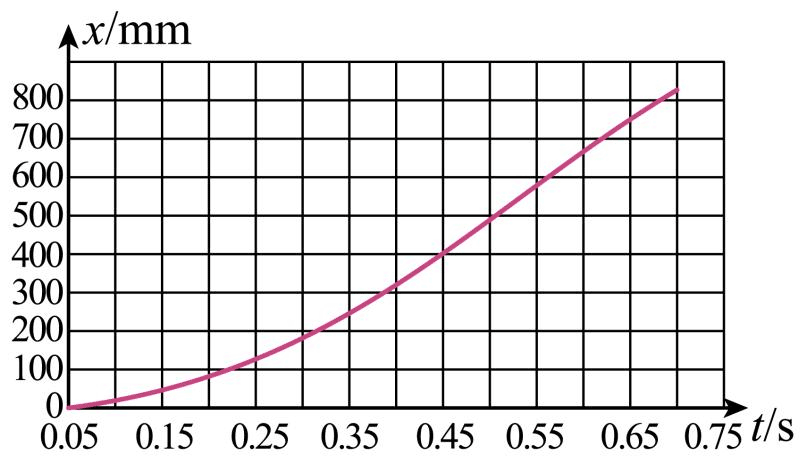
（3）在实验器材不变的情况下，能够减小实验误差测量误差的方法有：__________________（写出一种即可）

【答案】

（1）\(\frac{1}{{15}}\) s

（2）小于

（3）每张照片标记一次小球的位置

【解析】

（1）相邻标记位置之间的时间间隔是 T = 4×\(\frac{1}{{60}}\) s = \(\frac{1}{{15}}\) s。

（2）小球在 0.15 s ~ 0.35 s 时间内（Δt = 0.35s − 0.15 s = 0.20 s）位移 Δx = 240 mm – 40 mm = 200 mm = 0.200 m，平均速度大小为 v₁ = Δx/Δt = 1.0 m/s；小球在 0.45 s ~ 0.65 s 时间内（Δt = 0.65 s − 0.45 s = 0.20 s）位移 Δx = 750 mm – 400 mm = 350 mm = 0.350 m，平均速度大小为 v₂ = Δx/Δt = 1.75 m/s；由此可知小球在 0.15 s ~ 0.35 s 时间内平均速度的大小小于小球在 0.45 s ~ 0.65 s 时间内的平均速度的大小。

（3）在实验器材不变的情况下，能够减小实验误差测量误差的方法有：每张照片标记一次小球的位置。

 

12．某兴趣小组使用如图 1 电路，探究太阳能电池的输出功率与光照强度及外电路电阻的关系，其中 P 为电阻箱，R₀ 是阻值为 37.9 kΩ 的定值电阻，E 是太阳能电池，μA 是电流表（量程 0 ~ 100 μA，内阻 2.10 kΩ）

  

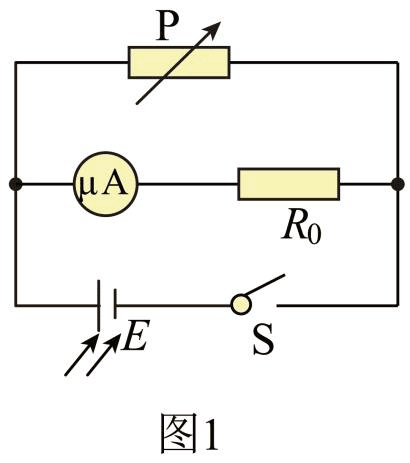
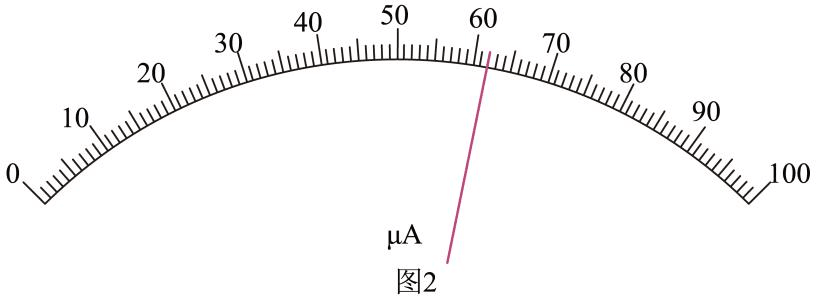
（1）实验中若电流表的指针位置如题图 2 所示，则电阻箱 P 两端的电压是_______V。（保留3位有效数字）

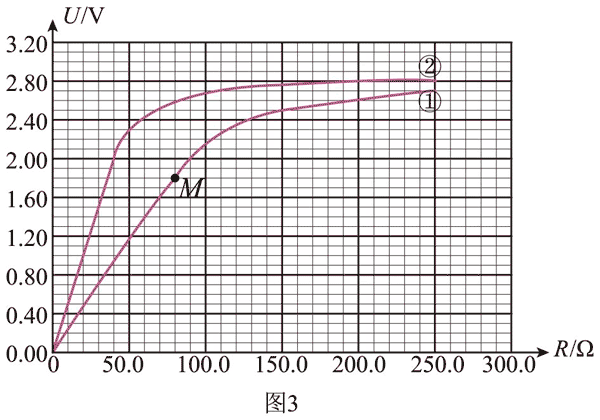
（2）在某光照强度下，测得太阳能电池的输出电压 U 与电阻箱 P 的电阻 R 之间的关系如图3中的曲线①所示。不考虑电流表和电阻 R₀ 消耗的功率，由该曲线可知，M 点对应的太阳能电池的输出功率是_______mW。（保留3位有效数字）

（3）在另一更大光照强度下，测得 U-R 关系如图3中的曲线②所示。同样不考虑电流表和电阻 R₀ 消耗的功率，与曲线①相比，在电阻 R 相同的情况下，曲线②中太阳能电池的输出功率__________（选填“较小”、“较大”），由图像估算曲线②中太阳能电池的最大输出功率约为________mW。（保留3位有效数字）

【答案】

（1）2.48

（2）40.5

（3）较大，66.7

【解析】

（1）根据电流表读数规则，电流表读数是 I = 62.0 μA = 6.20×10⁻⁵ A。电阻箱 P 两端的电压是 U = I（r_g + R₀） = 6.20×10⁻⁵×（2.10 + 37.9）×10³ V = 2.48 V。

（2）M点对应的电压 U = 1.80 V，电阻 R = 80.0 Ω，太阳能电池的输出功率 P = U²/R = 4.05×10⁻² W = 40.5 mW。

（3）与曲线①相比，在电阻 R 相同的情况下，曲线②中太阳能电池的电压较大，由 P = U²/R 可知，曲线②中太阳能电池的输出电功率较大。由图像②可知，太阳能电池电动势为E = 2.80 V，太阳能电池的内阻随外接电阻 R 的增大而减小，可估算出当 R = 30 Ω 时电池内阻约为 30 Ω，太阳能电池输出功率最大，最大输出电功率 P = E²/4R = 0.0667 W = 66.7 mW。

 

13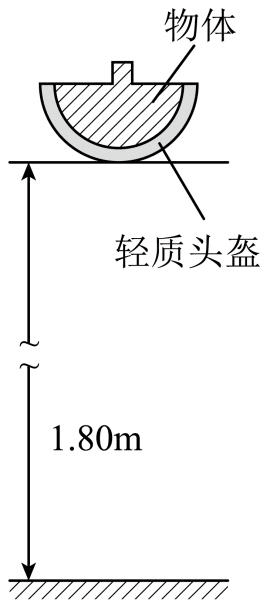．我国规定摩托车、电动自行车骑乘人员必须依法佩戴具有缓冲作用的安全头盔。小明对某轻质头盔的安全性能进行了模拟实验检测。某次，他在头盔中装入质量为 5.0 kg 的物体（物体与头盔密切接触），使其从 1.80 m 的高处自由落下，并与水平地面发生碰撞，头盔厚度被挤压了 0.03 m 时，物体的速度减小到零。挤压过程不计物体重力，且视为匀减速直线运动，不考虑物体和地面的形变，忽略空气阻力，重力加速度 g 取 10 m/s²。求：

（1）头盔接触地面前瞬间的速度大小；

（2）物体做匀减速直线运动的时间；

（3）物体在匀减速直线运动过程中所受平均作用力的大小。

【答案】

（1）v = 6 m/s。

（2）t = 0.01 s

（3）F = 3000 N

 

14．如图1所示的 Oxy 竖直平面内，在原点 O 有一粒子源，可沿 x 轴正方向发射速度不同、比荷均为 \(\frac{q}{m}\) 的带正电的粒子。在 x ≥ L 的区域仅有垂直于平面向内的匀强磁场；x < L 的区域仅有如图2所示的电场，0~t₀ 时间内和 2t₀ 时刻后的匀强电场大小相等，方向相反（0 ~ t₀ 时间内电场方向竖直向下），t₀ ~ 2t₀ 时间内电场强度为零。在磁场左边界 x = L 直线上的某点，固定一粒子收集器（图中未画出）。0 时刻发射的 A 粒子在 t₀ 时刻经过左边界进入磁场，最终被收集器收集；B 粒子在 \(\frac{{{t_0}}}{3}\) 时刻以与 A 粒子相同的发射速度发射，第一次经过磁场左边界的位置坐标为（L，−\(\frac{{4L}}{9}\)）；C 粒子在 t₀ 时刻发射，其发射速度是 A 粒子发射速度的 \(\frac{1}{4}\)，不经过磁场能被收集器收集。忽略粒子间相互作用力和粒子重力，不考虑边界效应。

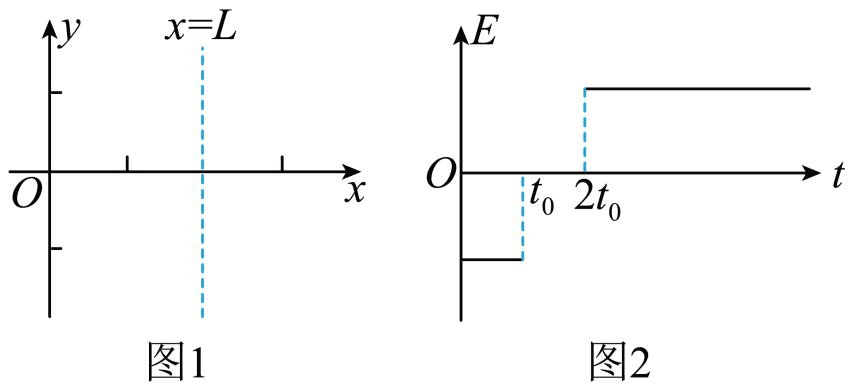
（1）求电场强度 E 的大小；

（2）求磁感应强度 B 的大小；

（3）设 2t₀ 时刻发射的粒子能被收集器收集，求其有可能的发射速度大小。

【答案】

（1）E = \(\frac{{Lm}}{{qt_0^2}}\)

（2）B = \(\frac{{2m}}{{5q{t_0}}}\)

（3）\(\frac{L}{{3{t_0}}}\)，\(\frac{4L}{{5{t_0}}}\)，\(\frac{L}{{t_0}}\)

 

15．图1和图2中曲线 Ⅰ、Ⅱ、Ⅲ 分别描述了某物理量随分之间的距离变化的规律，r₀为平衡位置。现有如下物理量：①分子势能，②分子间引力，③分子间斥力，④分子间引力和斥力的合力，则曲线 Ⅰ、Ⅱ、Ⅲ 对应的物理量分别是__________（在给出的4个选项中。只有一个符合要求的）

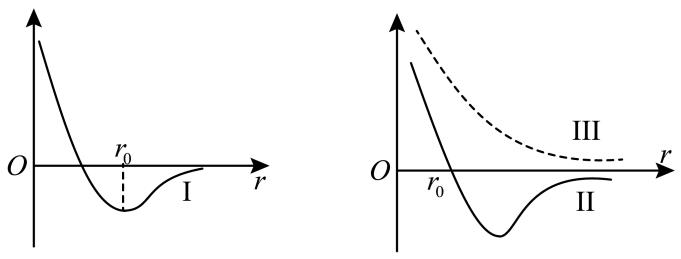
A．①③②           B．②④③           C．④①③           D．①④③

【答案】

D

【解析】

根据分子处于平衡位置（即分子之间距离为 r₀）时分子势能最小可知，曲线 Ⅰ 为分子势能随分子之间距离 r 变化的图像；

根据分子处于平衡位置（即分子之间距离为 r₀）时分子力为零，可知曲线 Ⅱ 为分子力随分子之间距离 r 变化的图像；

根据分子之间斥力随分子之间距离的增大而减小，可知曲线 Ⅲ 为分子斥力随分子之间距离 r 变化的图像；选项 D 正确。

 

15．定高气球是种气象气球，充气完成后，其容积变化可以忽略。现有容积为 V₁ 的某气罐装有温度为 T₁、压强为 p₁ 的氦气，将该气罐与未充气的某定高气球连通充气。当充气完成后达到平衡状态后，气罐和球内的温度均为 T₁，压强均为 kp₁，k 为常数。然后将气球密封并释放升空至某预定高度，气球内气体视为理想气体，假设全过程无漏气。

①求密封时定高气球内气体的体积；

②若在该预定高度球内气体重新达到平衡状态时的温度为 T₂，求此时气体的压强。

【答案】

（1）\(\frac{{1 - k}}{k}\)V₁

（2）\(\frac{{k{p_1}{T_2}}}{{{T_1}}}\)

 

 

16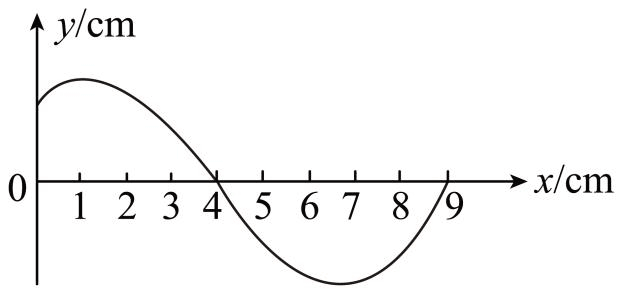．简谐横波沿x 轴正方向传播，题图为某时刻波形图。波源位于 x = 0 处，其位移随时间变化的关系为 y = sin（2πt）cm，则________（在给出的4个选项中。只有一个符合要求的）

A．此波的波长为 9 cm

B．此波的频率为 2 Hz

C．此波的波速为 0.1 m/s

D．此时波源沿 y 轴正方向运动

【答案】

C

【解析】

由波形图可知，此波的波长 λ = 10 cm，选项 A 错误；

由 ω = 2π = 2πf 可得此波的频率 f = 1 Hz，选项 B 错误；

由 ω = 2π = \(\frac{{2\pi }}{T}\) 可得 T = 1 s，由 λ = vT 可得此波的传播速度 v = 0.1 m/s，选项C正确；

此时波源沿 y 轴负方向运动，选项D错误。

 

16．如图所示，一直角棱镜 ABC，∠A = 90°，AC = 1。从 AB 边界面垂直入射的甲、乙两种不同频率的单色光，在棱镜中传播速度分别为 k₁c 和 k₂c（0 < k₁ < k₂ < 1，c 为真空中的光速），甲光第一次到达 BC 边恰好发生全反射。求：

（1）该棱镜分别对甲光和乙光的折射率；

（2）BC 边的长度。

【答案】

（1）n₁ = \(\frac{1}{{{k_1}}}\)，n₂ = \(\frac{1}{{{k_2}}}\)

（2）L = \(\frac{1}{{{k_1}}}\)