1．如图所示是电流天平原理示意图，使用电流天平可测量通电导线在磁场中所受的安培力。长方形线圈 abcd 共绕 15 匝，底边 bc 长 5 cm，挂在等臂天平的左端，并使线圈的 bc 边水平地悬于某一匀强磁场中，线圈平面跟磁场垂直。先使天平保持平衡，然后在线圈内通入 0.5 A 的电流，天平失去平衡。设此时右盘上升，为使天平重新达到平衡，需在右端盘内再加入 37.5 g 砝码。求：

（1）线圈中电流的方向；

（2）匀强磁场的磁感应强度大小。

【答案】

电流方向是 a → b → c → d。B = 0.98 T

【解析】

分析：n 匝线圈通过电流 I 受到的安培力可以等效为单匝线圈通过 nI 大小的电流受到的安培力。

解：（1）线圈通电流后，ab 边和 cd 边在磁场部分所受的安培力沿水平方向等值反向而彼此平衡；bc 边所受安培力方向应竖直向下，才会导致右盘上升而使天平失去平衡，由左手定则可判断线圈中的电流方向是 a → b → c → d。

（2）由于天平两臂等长，为使天平重新平衡，bc 边 n 匝导线所受的安培力应该等于天平右端增加的砝码的重力。设 bc 边长为 L，通过线圈的电流为 I，匀强磁场的磁感应强度为 B，天平右端增加的砝码质量为 Δm，则有

\[nBIL = \Delta mg\]

由此可得匀强磁场的磁感应强度

\[B = \frac{{\Delta mg}}{{nIL}} = \frac{{37.5 \times {{10}^{ - 3}} \times 9.8}}{{15 \times 0.5 \times 0.05}}{\rm{T}} = 0.98\;{\rm{T}}\]

 

2．如图所示，相距 L = 10 cm 的两条平行导轨组成的平面与水平面夹角 θ = 30°，导轨两端 M、N 间接一电动势 E = 3 V、内阻 r = 0.5 Ω 的电源，垂直于导轨平面有一匀强磁场，将质量 m = 10 g 的金属棒垂直放在平行导轨上，金属棒恰能静止不动。若两导轨间金属棒的电阻 R = 1 Ω，试回答：

（1）垂直于导轨平面的磁场方向是向上还是向下？

（2）磁场的磁感应强度大小是多少？（导轨与金属棒接触良好，导轨与金属棒间摩擦力以及导轨电阻不计）

【答案】

（1）垂直于导轨平面向下。

（2）B ≈ 0.25 T

【解析】

分析：以平行导轨上的金属棒为研究对象进行受力分析。由闭合电路欧姆定律求电流，由力的平衡条件求安培力，由安培力公式求磁感应强度。

解：（1）以金属棒为研究对象，金属棒在导轨上处于平衡状态，受到重力 mg、弹力 F_N 和安培力 F 的作用。因磁场垂直于导轨平面，电流垂直于导轨，安培力 F 的方向平行于导轨。再由力的平衡条件可知，安培力应平行于导轨向上，如图 5–9 所示。而电流方向已知，由左手定则可判断磁感应强度的方向应垂直于导轨平面向下。

（2）由于金属棒处于静止状态，则根据力的平衡条件，金属棒所受重力在斜面方向上的分力与安培力大小相等、方向相反，设通过金属棒的电流为 I，则有

\[mg\sin \theta = BIL\]

在电源、导轨、金属棒构成的回路中，由闭合电路欧姆定律 I = \(\frac{E}{{R + r}}\)，代入得磁感应强度

\[B = \frac{{(R + r)mg\sin \theta }}{{LE}} = \frac{{(1 + 0.5) \times 10 \times {{10}^{ - 3}} \times 9.8 \times 0.5}}{{0.1 \times 3}}{\rm{T}} \approx 0.25\;{\rm{T}}\]

 

3．图中各图已经分别标明电流 I、磁场 B 和安培力 F 这三个物理量中的两个量的方向，试在图中标出第三个量的方向。

【答案】

（a）电流 I 水平向右

（b）安培力 F 垂直导线向左上方

（c）磁场 B 水平向左

（d）无安培力 F

【解析】

命题意图：运用左手定则判断安培力的方向。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅰ）。

 

4．如图所示，在磁感应强度为 4×10⁻² T 的匀强磁场中有一根与磁场方向垂直、长 8 cm 的通电直导线 ab。通电直导线 ab 所受的安培力大小为 1×10⁻² N，方向垂直纸面向外，导线中电流的大小为多少？方向如何？

【答案】

F = BIL

I = \(\frac{F}{{BL}}\) = \(\frac{{1 \times {{10}^{ - 2}}}}{{4 \times {{10}^{ - 2}} \times 8 \times {{10}^{ - 2}}}}\) A = 3.125 A

根据左手定则可判断导线中电流方向为 b→a

【解析】

命题意图：能判断安培力的方向，会计算安培力的大小。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学论证（Ⅱ）。

 

5．有两根通电平行直导线，分别通入如图所示的同方向电流和反方向电流。两根平行直导线之间是否存在相互作用力？如存在，作用力的方向如何？用虚线在图中大致描绘出通电后两根导线的实际形状。

【答案】

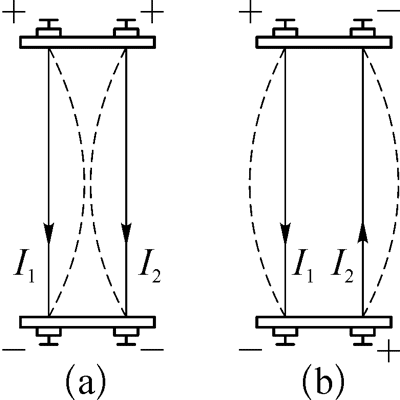
两根通电平行直导线间存在相互作用力；同方向电流间相互吸引，反方向电流间相互排斥。（虚线：同方向电流向内侧形变，反方向电流向外侧形变，如图所示）

【解析】

命题意图：运用左手定则判断两根通电平行直导线间的相互作用，加深对安培力相关概念的理解。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

6．如图 5–17 所示，导线 ab 长 20 cm，用两根平行的、相同的弹簧将 ab 水平挂起，弹簧间有沿水平方向垂直于纸面向里的匀强磁场，磁场区域宽度 10 cm，磁感应强度大小为 0.5 T，导线 ab 所受重力大小为 0.1 N。为了使弹簧不发生形变，导线内电流的方向和大小应如何？

【答案】

弹簧不发生形变，两侧的弹簧对导线 ab 没有弹力。根据平衡条件：F = G；又由 F = BIL

可得      I = \(\frac{F}{{BL}}\) = \(\frac{G}{{BL}}\) = \(\frac{{0.1}}{{0.5 \times 0.1}}\) A = 2 A

安培力的方向竖直向上，根据左手定则可判断导线内电流方向为 a→b

【解析】

命题意图：运用安培力综合分析解决问题。

主要素养与水平：科学推理（Ⅱ）；科学论证（Ⅱ）。

 

7．如图所示是一种磁电式仪表的原理图，可以用它来测量电流的大小。P 是带指针绕在铁芯上可转动的线圈，线圈置于磁场中，A、B 为两个接线柱。如指针向右偏转，电流从哪个接线柱流入电表？

【答案】

若通电后指针 P 向右偏转，则说明圆柱形铁芯左侧受到的安培力向上，右侧受到的安培力向下。根据左手定则判断线圈内的电流方向，可得电流是由 A 接线柱流入电表的。

【解析】

命题意图：了解安培力在生产生活中的应用，应用安培力分析磁电式仪表的工作原理。

主要素养与水平：科学推理（Ⅱ）；科学本质（Ⅲ）。

 

8．电磁炮基本原理如图所示。抛射体可在平行轨道自由移动，并与轨道保持良好的电接触。电流从一条轨道流入，通过导电的抛射体后从另一条轨道流回。轨道电流可在抛射体处形成近似垂直于轨道面的磁场，磁感应强度的大小与电流成正比。抛射体在轨道上受到安培力的作用而沿导轨加速射出。如欲使抛射体的出射速度增加，理论上可采用哪些办法？

【答案】

可采用分级评分体现科学思维水平，水平越高得分越高。

根据匀变速直线运动规律可得，可增大抛射体的加速度及其作用的时间；从动能定理可得，可增大抛射体的合外力及其作用的位移；从动量定理可得，可增大抛射体的合外力及其作用的时间。

BIL − F_阻 = ma；a = \(\frac{{BIL}}{m}\) − \(\frac{{{F_阻}}}{m}\)；v = \(\sqrt {2as} \) = \(\sqrt {2\left( {\frac{{BIL}}{m} - \frac{{{F_阻}}}{m}} \right)s} \) = \(\sqrt {2\frac{{(k{I^2}L - {F_阻})s}}{m}} \)

理论上可采用的方法为：增大轨道和抛射体的宽度 L；增大轨道长度 s；增大电流 I；减小抛射体质量 m；减小抛射体受到的阻力 F_阻。

（学生其他合理的科学推理和科学论证均可，如：建模考虑受到变化的阻力，抛射体除了受到轨道的阻力外还受到空气对抛射体的阻力，空气的阻力又与速度或者速度的平方成正比，故抛射体射出前可能已经达到平衡状态，以终极速度射出等。）

水平 2：通过文字叙述进行合理的分析。

水平 3：进行建模但不考虑阻力的影响。

水平 4：进行建模考虑阻力的影响。

【解析】

命题意图：运用安培力综合分析实际问题，培养模型建构、科学推理和质疑创新的能力。

主要素养与水平：运动与相互作用观念（Ⅳ）；科学推理（Ⅳ）；科学论证（Ⅲ）。

 

9．如图所示，一束粒子包含有质子（带正电）、电子（带负电）和光子（不带电）三种粒子。粒子束中的粒子沿水平向右的方向射入垂直纸面向里的匀强磁场中。请分析并描述粒子束进入匀强磁场后的偏转情况。

【答案】

分析：根据粒子束中的粒子所带的电荷和左手定则即可判断。

解：粒子束内的光子不带电，不受磁场的任何影响。质子和电子带有电荷，会受洛伦兹力作用。粒子束内的光子不发生偏转保持原有速度匀速前进；粒子束内的质子带正电，由左手定则可知所受洛伦兹力向上，所以射入匀强磁场后质子束向上偏转；粒子束内的电子带负电，使用左手定则时，四指方向应与电子运动方向相反，可判定电子束进入匀强磁场后向下偏转。

 

10．电子以 6×10⁶ m/s 的速率垂直射入磁感应强度为 0.5 T 的匀强磁场中，电子受到的洛伦兹力的大小为何？如果电子射入磁场时的速度 v 与磁感应强度 B 的方向间的夹角是 180°，则电子所受的洛伦兹力大小为何？

【答案】

运动电荷受到的洛伦兹力大小为 f = qvB = 1.6×10⁻¹⁹×6×10⁶×0.5 N = 4.8×10⁻¹³ N。

如电荷运动方向与磁场方向在同一直线上，运动电荷受到的洛伦兹力大小为零。

【解析】

命题意图：会计算洛伦兹力的大小。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学论证（Ⅱ）。

 

11．如图所示，试判断运动电荷在磁场中所受洛伦兹力的方向。

【答案】

竖直向上，竖直向上，垂直纸面向外

【解析】

命题意图：运用左手定则判断洛伦兹力的方向。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅰ）。

 

12．如图所示，阴极射线管（A 为阴极）放在蹄形磁体的 N、S 两极间，阴极射线管的 A、B 两端分别通过导线连接到直流高压电源的哪个电极？若无磁体，电子的运动方向如何？磁体如图示情境放置，电子束运动轨迹的偏转情况如何？

【答案】

阴极射线管的 A 端连接直流高压电源的负极，B 端连接电源的正极，电子的运动方向由 A→B，电子束运动轨迹向上偏转。

【解析】

命题意图：运用左手定则判断洛伦兹力的方向，解释电子束在磁场中偏转的原因。

主要素养与水平：运动与相互作用观念（Ⅲ）；科学推理（Ⅱ）。

 

13．如果一个电子在通过空间某区域时不偏转，是否能肯定该区域中没有磁场？如果一个电子在通过空间某区域时发生侧向偏转，是否能肯定该区域中存在着磁场？试说明理由。

【答案】

电子通过空间某区域时不偏转，该区域不一定没有磁场。如磁场方向与电子运动方向在同一条直线上，运动电子不受洛伦兹力作用故不发生偏转。也有可能空间区域内既存在磁场也存在电场，电场力和洛伦兹力平衡所以不发生偏转。

电子在通过空间某区域发生侧向偏转，可能是电子通过电场区域受到电场力的作用，也可能是电子通过磁场区域受到洛伦兹力的作用，所以该区域中不一定存在磁场。

【解析】

命题意图：将静电场知识和磁场知识相关联分析带电粒子偏转的原因，电场力和磁场力都能使带电粒子发生偏转。

主要素养与水平：运动与相互作用观念（Ⅲ）；科学推理（Ⅱ）。

 

14．某区域存在一竖直向上的匀强磁场，磁场的磁感应强度大小为 1.2×10⁻³ T。动能为 5.3 MeV 的质子由南向北水平通过磁场区域，则质子受到的洛伦兹力的大小和方向如何？（质子质量为 1.67×10⁻²⁷ kg，忽略地球磁场）

【答案】

E_k = \(\frac{1}{2}\)mv²

v = \(\sqrt {\frac{{2{E_k}}}{m}} \) = \(\sqrt {\frac{{2 \times 5.3 \times {{10}^6} \times 1.6 \times {{10}^{ - 19}}}}{{1.67 \times {{10}^{ - 27}}}}} \) m/s = 3.19×10⁷ m/s

f = qvB = 1.6×10⁻¹⁹×3.19×10⁷×1.2×10⁻³ N = 6.12×10⁻¹⁵ N

洛伦兹力的方向：水平向东。

【解析】

命题意图：针对匀强磁场与带电粒子运动方向垂直的情况，会计算带电粒子所受洛伦兹力的大小，能 判断洛伦兹力的方向。

主要素养与水平：能量观念（Ⅱ）；科学推理（Ⅲ）；科学论证（Ⅱ）。

 

15．如图所示，偏转极板间存在匀强电场，匀强电场的电场强度为 1.5 kV/m，方向竖直向下；线圈系统（图中未显示）产生的匀强磁场的磁感应强度为 0.4 T，方向垂直纸面向里。若灯丝发射的电子能沿直线匀速通过电场和磁场区域，那么，电子运动的速度大小是多少？（忽略电子所受重力）

【答案】

忽略电子所受重力，运动电荷在电场中受到电场力 qE，竖直向上。运动电荷在磁场中 还受到洛伦兹力 qvB，竖直向下。电子匀速的通过电场和磁场区域，合力为零

qE = qvB

v = \(\frac{E}{B}\) = \(\frac{{1.5 \times {{10}^3}}}{{0.4}}\) m/s = 3.75×10³ m/s

【解析】

命题意图：将静电场知识、磁场知识与力学知识相关联，培养学生综合分析问题和解答实际问题的能力。

主要素养与水平：运动与相互作用观念（Ⅲ）；科学推理（Ⅲ）；科学论证（Ⅱ）。

 

16．一个初速度为零的质子，经过电压 U = 1.3×10³ V 的电场加速后垂直进入磁感应强度 B 为 0.20 T 的匀强磁场。质子的质量 m = 1.67×10⁻²⁷ kg， 电荷量 q = 1.6×10⁻¹⁹ C。求：

（1）质子进入磁场时的速度大小；

（2）质子在磁场中运动的轨道半径；

（3）质子做匀速圆周运动的周期。

【答案】

（1）v ≈ 5.0×10⁵ m/s

（2）r ≈ 2.6×10⁻² m

（3）T ≈ 3.3×10⁻⁷ m

【解析】

分析：电场可以使带电粒子加速，也可以使它偏转；带电粒子垂直进入磁场只能使带电粒子偏转。本题中质子受电场加速，然后在匀强磁场中做匀速圆周运动。

解：（1）初速度为零的质子在电场中被加速，获得动能。质子在电场中得到的动能等于电场对它所做的功，设质子进入磁场时的速度大小为 v，则有

\[\frac{1}{2}m{v^2} = qU\]

所以                                                              \(\begin{array}{l}v = \sqrt {\frac{{2qU}}{m}} \\ = \sqrt {\frac{{2 \times 1.6 \times {{10}^{ - 19}} \times 1.3 \times {{10}^3}}}{{1.67 \times {{10}^{ - 27}}}}} \;{\rm{m/s}}\end{array}\)

                                                                      ≈ 5.0×10⁵ m/s

（2）质子垂直射入匀强磁场，做匀速圆周运动。设质子做匀速圆周运动的半径为 r，它在磁场中受到的洛伦兹力提供质子做匀速圆周运动所需的向心力，得

\[qvB = m\frac{{{v^2}}}{r}\]

所以，质子在磁场中运动的轨道半径

\[\begin{array}{l}r = \frac{{mv}}{{qB}}\\ = \frac{{1.67 \times {{10}^{ - 27}} \times 5 \times {{10}^5}}}{{1.6 \times {{10}^{ - 19}} \times 0.20}}\;{\rm{m}}\end{array}\]

                                                             ≈ 2.6×10⁻² m

（3）质子做匀速圆周运动的周期

\[\begin{array}{l}T = \frac{{2\pi r}}{v}\\ = \frac{{2 \times 3.14 \times 2.6 \times {{10}^{ - 2}}}}{{5 \times {{10}^5}}}\;{\rm{s}}\end{array}\]

                                                            ≈ 3.3×10⁻⁷ m

 

17．如图所示是电子在匀强磁场中做匀速圆周运动的轨迹，匀强磁场的方向垂直纸面向里。电子是顺时针还是逆时针运动？试简述理由。

【答案】

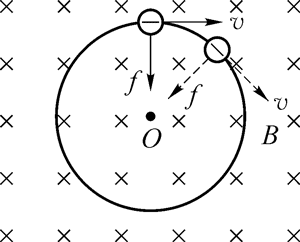
电子顺时针运动。运动电荷在磁场中受到的洛伦兹力提供电子做匀速圆周运动的向心力，指向圆心。由左手定则可判断正电荷应逆时针转动，从而可得电子顺时针运动。

【解析】

命题意图：引导学生判断洛伦兹力与电荷运动之间的关系。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

18．足够大的匀强磁场中有两个电子从出发点同时射出，分别以速度 v 和 2v 垂直于磁场方向运动，哪个电子先回到出发点？试简述理由。

【答案】

带电粒子在匀强磁场中做匀速圆周运动 qvB = m \(\frac{{{v^2}}}{r}\)，可得 r = \(\frac{{mv}}{{qB}}\)。圆周运动的周期 T = \(\frac{{2\pi m}}{{qB}}\)。由此可见，电子在磁场中做匀速圆周运动的周期与速率 v 无关，因此两个电子同时回到出发点。

【解析】

命题意图：了解带电粒子在匀强磁场中做匀速圆周运动的周期跟轨道半径 r 及速率 v 无关。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

19．洛伦兹力演示仪用于观察运动电子在磁场中的运动。判断下列说法是否正确，简述理由。

（1）不加磁场时电子束的径迹是直线。

（2）加磁场并调整磁感应强度可使电子束径迹形成一个圆周。

（3）保持磁感应强度不变，增大出射电子的速度，电子束圆周的半径减小。

（4）保持出射电子的速度不变，增大磁感应强度，电子束圆周的半径减小。

【答案】

（1）正确      （2）正确      （3）不正确，电子束圆周的半径会增大        （4）正确

【解析】

命题意图：运用洛伦兹力分析带电粒子在匀强磁场中的圆周运动的半径大小。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

20．一个电子在磁感应强度为 4 mT 的匀强磁场区域中做匀速圆周运动，电子受到的洛伦兹力大小为 3.2×10⁻¹⁵ N，电子的质量为 9.1×10⁻³¹ kg。计算电子做匀速圆周运动的速度大小、轨道半径和周期。

【答案】

参考解答：f = qvB

可得 v = \(\frac{f}{{qB}}\) = \(\frac{{3.2 \times {{10}^{ - 15}}}}{{1.6 \times {{10}^{ - 19}} \times 4 \times {{10}^{ - 3}}}}\) m/s = 5×10⁶ m/s

f = m \(\frac{{{v^2}}}{r}\)

可得 r = \(\frac{{m{v^2}}}{f}\) = \(\frac{{9.1 \times {{10}^{ - 31}} \times {{(5 \times {{10}^6})}^2}}}{{3.2 \times {{10}^{ - 15}}}}\) m = 7.11×10⁻³ m

T =  \(\frac{{2\pi r}}{v}\) =  \(\frac{{2 \times 3.14 \times 7.11 \times {{10}^{ - 3}}}}{{5 \times {{10}^6}}}\) s = 8.93×10⁻⁹ s

【解析】

命题意图：运用洛伦兹力公式解答带电粒子在匀强磁场中的圆周运动问题。

主要素养与水平：科学推理（Ⅱ）；科学论证（Ⅱ）。

 

21．如图所示，质谱仪的离子源 P 产生的离子经正下方 S₁ 和 S₂ 之间的电场加速后射入速度选择器。速度选择器中的匀强电场 E 和匀强磁场 B 都垂直于离子速度 v，且 E 和 B 相互垂直，狭缝 S₃ 在离子源 P 的正下方。离子源 P 射出的离子并非都能通过狭缝 S₃ 进入磁场 B₀。试问：通过速度选择器后能射入狭缝 S₃ 的离子速率 v 需满足怎样的条件？

【答案】

参考解答：离子经加速后射入速度选择器，以正离子为例，正离子在磁场中受到向左的洛伦兹力和向右的电场力作用。粒子源 P 和狭缝 S₃ 在一条直线上，意味着正离子水平方向不发生侧向偏转，所以能从速度选择器射出的离子应受力平衡，即满足受到的电场力和洛伦兹力大小相等，方向相反，则有

qE = qvB

可得：通过速度选择器后射入狭缝 S₃ 的离子速率需要满足的条件是 v = \(\frac{E}{B}\)。

【解析】

命题意图：了解电场力和洛伦兹力都能使带电粒子偏转，理解质谱仪中速度选择器的原理和作用。

主要素养与水平：科学推理（Ⅲ）；科学本质（Ⅲ）。

 

22．如图所示，中性气体分子在容器 A 中被电离成离子，离子从 S₁ 的狭缝处离开时速度接近于零，进入 S₁ 和 S₂ 间电压为 U 的加速电场中被加速，再从 S₃ 的狭缝垂直进入匀强磁场，沿半圆轨迹运动并使记录底片在 P 处感光。离子的质量为 m、所带的电荷量为 q，匀强磁场的磁感应强度为 B，S₃ 缝到底片上 P 点的距离为 d。试证明：\(\frac{q}{m}\) = \(\frac{{8U}}{{{B^2}{d^2}}}\) 。

【答案】

离子在 S₁ 和 S₂ 之间的电场中被加速，根据动能定理

qU = \(\frac{1}{2}\) mv² − 0

离子在匀强磁场中作匀速圆周运动，根据牛顿第二定律

qvB = m \(\frac{{{v^2}}}{r}\)

结合几何关系，轨道半径为

r = \(\frac{1}{2}\) d

由 ①、②、③ 式可证明离子的荷质比 (\frac{e}{m}\) = \(\frac{{8U}}{{{B^2}{d^2}}}\)

【解析】

命题意图：理解质谱仪的基本原理，了解质谱仪如何测定带电粒子的荷质比。

主要素养与水平：运动与相互作用观念（Ⅳ）；能量观念（Ⅳ）；科学论证（Ⅳ）。

 

23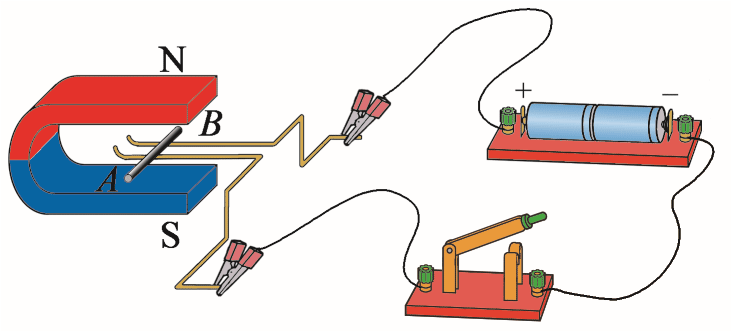．如图所示的蹄形磁体水平放置，在磁场中有一水平光滑导轨通过接线夹与导线相连，导轨上面搁有一导体细棒 AB。AB 棒、电源、开关等由导线连成回路。闭合开关，导体棒 AB 将如何运动？简述这一现象中能量的转化过程。

【答案】

闭合开关，导体棒中的电流由 B→A，根据左手定则可判断安培力方向向右，导体细棒由静止变为向右运动。这一现象中电能通过安培力做功转化为导体细棒的机械能。

【解析】

命题意图：通过实验认识安培力，能判断安培力的方向。

主要素养与水平：运动与相互作用观念（Ⅱ）；能量观念（Ⅱ）；科学推理（Ⅱ）。

 

24．在匀强磁场中的通电导线受到安培力的作用，其中安培力的方向、磁场的方向、通电导线的方向三者间是否都相互垂直？

【答案】

磁场的方向与通电导线的电流方向不一定需要垂直。安培力的方向既与磁场的方向垂直又与通电导线的电流方向垂直，安培力的方向垂直于磁场和电流所确定的平面。

【解析】

命题意图：知道安培力的方向垂直于电流和磁感应强度组成的平面。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学论证（Ⅱ）。

 

25．阴极射线管发射的电子束中的电子由左向右运动，其上方放置一根通有由左向右电流的直导线，直导线与阴极射线管平行。电子束的轨迹是否发生偏转？如偏转，则偏转方向如何？

【答案】

电子束的运动轨迹会发生偏转，电子束向下偏转。

【解析】

命题意图：知道通电直导线周围存在磁场，了解带电粒子在磁场中的偏转。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

26．平行轨道上有一辆平板小车，车上有一个通电线框，如图 5–43 所示。图中虚线框 1、2、3、4、5 等内部是磁场区域，磁场方向垂直纸面向里或向外。要使小车在图示位置时受到向右的安培力，虚线框 1、2 部分的磁场方向如何？平板小车经过磁场区域 2、3 位置时，如果仍要使小车受到向右的推力，此时虚线框 2、3 部分的磁场方向应如何？怎样改变磁场方向才能使小车始终受到向右的推力？实际生活中哪种交通工具的驱动原理与此相仿？

【答案】

虚线框 1 内磁场垂直纸面向里、虚线框 2 内磁场垂直纸面向外；虚线框 2 内磁场垂直纸面向里、虚线框 3 内磁场垂直纸面向外；虚线框内交替改变磁场的方向：使闭合电路的左侧到达的区域磁场总是垂直纸面向里，右侧到达的区域磁场总是垂直纸面向外。实际生活中磁悬浮列车的驱动原理与此原理相同。

【解析】

命题意图：用左手定则判断安培力的方向，了解安培力在生产生活中的应用。

主要素养与水平：运动与相互作用观念（Ⅲ）；科学推理（Ⅲ）；科学本质（Ⅱ）。

 

27．图中的曲线显示一带电粒子运动的轨迹。a、b 区域均为匀强磁场，粒子在 a、b 磁场内的轨迹均为圆周的四分之一；离开 b 磁场区域后，带电粒子在两个带等量异号电荷的平行金属板之间运动，并向正极板偏转。试判断带电粒子带正电荷还是负电荷？a、b 区域内的磁场方向如何？

【答案】

带电粒子带负电荷 a 区域磁场垂直纸面向里，b 区域磁场垂直纸面向外。

【解析】

命题意图：用左手定则判断洛伦兹力的方向。

主要素养与水平：运动与相互作用观念（Ⅲ）；科学推理（Ⅱ）。

 

28．如图所示为电子通过两个匀强磁场区域的路径，两个区域的磁感应强度分别为 B₁ 和 B₂，电子在每个区域内的轨迹都是半圆。则：B₁ 和 B₂ 相比，哪个区域内的磁感应强度较大？B₁ 和 B₂ 区域内的磁场方向如何？电子在 B₁ 区域运动的时间和在 B₂ 区域运动的时间相比，哪个较长？简述理由。

【答案】

B₁ 区域磁感应强度更大。B₁ 垂直纸面向里，B₂ 垂直纸面向外。t₁ 小于 t₂。

qvB = m \(\frac{{{v^2}}}{r}\) 由此得出 B = \(\frac{{mv}}{{qr}}\)。同一个电子 m、q 相同，带电粒子在匀强磁场中做匀速圆周运动，速率 v 不变，则 B ∝ \(\frac{1}{r}\)。由图像可看出 r₁ < r₂，所以 B₁ > B₂。

由洛伦兹力提供圆周运动所需的向心力，根据左手定则可得。B₁ 垂直纸面向里，B₂ 垂直纸面向外。

r = \(\frac{{mv}}{{qB}}\) 代入 T = \(\frac{{2\pi r}}{v}\)，可得 T = \(\frac{{2\pi m}}{{qB}}\)，在磁场区域所花的时间 t = \(\frac{1}{2}\)T。同一个电子 m、q 相同，则 T ∝ \(\frac{1}{B}\)。因为 B₁ > B₂，所以 t₁ < t₂。

【解析】

命题意图：运用洛伦兹力公式计算带电粒子在匀强磁场中圆周运动的半径和周期。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅲ）。

 

29．用绝缘细线悬挂的带正电塑料小球做简谐运动。如增加一个如图 5–46 所示的匀强磁场，带电塑料小球每次经过平衡位置时，速率是否发生变化？小球摆动的周期是否改变？简述理由。

【答案】

速率不变，周期不变。

运动的带电塑料小球在匀强磁场中受到的洛伦兹力始终与位移垂直，故洛伦兹力不做功。只有重力做功，机械能守恒，所以当小球每次通过平衡位置时，动能相同，速率不变。根据左手定则可判断洛伦兹力始终沿细线方向，简谐运动的回复力不变，故小球摆动的周期不变。

【解析】

命题意图：运用洛伦兹力和力学知识，结合能量观念综合分析带电小球在匀强磁场中的周期运动。

主要素养与水平：模型建构（Ⅲ）；科学推理（Ⅳ）。

 

30．如图所示，带电小球质量为 m，用细线悬挂于 O 点并在竖直平面内摆动，最大摆角为 60°，磁场垂直于小球摆动的平面向里。当小球从左边最大摆角处摆到最低点时，细线上的拉力恰为零。试问小球带正电还是带负电？小球从右边最大摆角处摆到最低点时，细线上的拉力是否仍为零？简述理由。

【答案】

小球带正电，细线上的拉力不为零，拉力一定变大。

小球从左边最大摆角处摆到最低点时，细线上的张力恰为零，说明最低点受力情况如图 1 所示，洛伦兹力竖直向上根据左手定则可判断小球带正电。

      

当小球从右边最大摆角处摆到最低点时，速率仍为 v，对小球受力分析如图 2 所示，小球所受张力、洛伦兹力和重力的合力提供向心力。因此细线上的拉力一定变大。

【解析】

命题意图：运用洛伦兹力和力学知识，结合能量观念综合分析带电小球经匀强磁场区域的圆周运动。

主要素养与水平：科学推理（Ⅲ）。

 

31．质量为 10 g、电荷量为 +80 μC 的带电小球以 20 km/s 的速度沿直线匀速通过水平方向的匀强磁场，带电小球运动的速度方向与磁场方向垂直。求匀强磁场的磁感应强度大小。（g 取 10 m/s²）

【答案】

mg = qvB

B = \(\frac{{mg}}{{qv}}\) = \(\frac{{10 \times {{10}^{ - 3}} \times 10}}{{80 \times {{10}^{ - 6}} \times 20 \times {{10}^3}}}\) T = 6.25×10⁻² T

【解析】

命题意图：运用洛伦兹力和力学知识，分析带电小球做匀速直线运动的原因。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学论证（Ⅱ）。

 

32．如图所示，两平行光滑导轨相距 L = 0.1 m，并与水平面成 θ = 37° 夹角，竖直向下的匀强磁场的磁感应强度 B = 0.2 T，将一个质量 m = 10 g 的导体棒 ab 与导轨相互垂直地搁在导轨上。为了使导体棒 ab 能静止在导轨上，导体棒内的电流的方向和大小应如何？

【答案】

a→b，3.75 A

画出导体棒 ab 的侧视图，根据电源正负极可得导体棒内电流方向 a→b，根据左手定则可判断通电导体棒受到水平向右的安培力 F 作用。

由 mgsinθ = Fcosθ 和 F = BIL 可得，I = \(\frac{{mg\tan \theta }}{{BL}}\) = \(\frac{{10 \times {{10}^{ - 3}} \times 10 \times \tan 37^\circ }}{{0.2 \times 0.1}}\) A = 3.75 A

【解析】

命题意图：运用安培力和共点力平衡知识分析解决问题，加深对安培力的认识。

主要素养与水平：科学推理（Ⅲ）；科学论证（Ⅲ）。

 

33．如图所示，一束正离子束以速度 v 进入垂直于纸面的匀强磁场，该匀强磁场的磁感应强度为 B，用固定的探测器测得正离子运动的圆周直径为 d。已知单个正离子所带的电荷量为 +e，质量为 20 u（u 为原子质量单位，1 u ≈ 1.660 5×10⁻²⁷ kg），则：

（1）该匀强磁场的方向如何？

（2）若在该正离子束内还有质量为 22 u、电荷量和速率都与质量为 20 u 的正离子相同的另一种正离子。试在图中定性地描绘出质量为 22 u 的正离子在磁场中的运动轨迹。为了在固定的探测器上探测到质量为 22 u 的正离子，匀强磁场的磁感应强度应如何变化？

【答案】

（1）匀强磁场的方向垂直纸面向里。

（2）r = \(\frac{{mv}}{{qB}}\)，d = 2r = \(\frac{{2mv}}{{qB}}\) 可知在 v、q、B 一定时，离子的质量 m 越大，圆周运动的直径越大。

定性描绘出这些正离子在磁场中的运动轨迹如图所示。

为了在固定探测器上探测到这些离子，即圆周运动的直径 d 保持不变，随着离子的质量 m 的增大，匀强磁场的磁感应强度 B 也需增大。

【解析】

命题意图：了解带电粒子在匀强磁场中的偏转及其应用，知道质谱仪为何可区分同位素。

主要素养与水平：科学推理（Ⅲ）；科学论证（Ⅲ）；科学本质（Ⅲ）。

 

34．如图所示，光滑绝缘杆与水平面保持 θ 角，匀强磁场的磁感应强度为 B。一个可自由滑动的带正电小环套在杆上，质量为 m、电荷量为 q。若小环下滑过程中对杆的压力为零，则小环的速度有多大？

【答案】

对小环进行受力分析，根据平衡条件可得

qvB = mgcosθ

v = \(\frac{{mg\cos \theta }}{{qB}}\)

【解析】

命题意图：运用洛伦兹力和共点力平衡知识分析解决问题，加深对洛伦兹力的认识。

主要素养与水平：科学推理（Ⅲ）；科学论证（Ⅲ）。

 

35．某个带电粒子进入匀强磁场中，其速度垂直于磁场方向。带电粒子运动的周期 T 与磁感应强度 B 的倒数之间的关系如图所示。求此带电粒子的电荷量 q 与质量 m 之比。

【答案】

qvB = m\(\frac{{{v^2}}}{r}\)，由此得出 B = \(\frac{{mv}}{{qr}}\)。将 v = \(\frac{{2\pi r}}{T}\) 代入，可得

BT = 2π \(\frac{m}{q}\)

可由图像求出斜率 k = \(\frac{{22.5 - 8}}{{3 - 1}}\)×10⁻⁹ = 7.25×10⁻⁹

由 k = \(\frac{T}{{{B^{ - 1}}}}\) = BT = 2π \(\frac{m}{q}\)，可得带电粒子的电荷量与质量之比为

\(\frac{q}{m}\) = \(\frac{{2\pi }}{k}\) = \(\frac{{2\pi }}{{7.25 \times {{10}^{ - 9}}}}\) C/kg = 8.67×10⁸ C/kg

【解析】

命题意图：结合图像分析提高学生综合运用知识以及分析和解决问题的能力。

主要素养与水平：科学推理（Ⅳ）；科学论证（Ⅲ）。

 

36．如图所示是法拉第发现电磁感应现象的实验示意图，A、B 是套在同一铁芯上的两个线圈。试标出当开关 S 闭合的瞬间，与线圈 B 相连接的灵敏电流计中电流的方向。

【答案】

D → C

【解析】

分析：线圈 A 与电源接通的瞬间，线圈 A 中的磁通量发生变化，引起套在同一铁芯上闭合线圈 B 的磁通量相应变化，从而在线圈 B 中产生感应电流。

解：根据右手螺旋定则，线圈 A 中的磁感线穿过线圈 B 的方向如图 6–5（b）中的实线所示；电路接通瞬间，线圈 B 中的磁场增强，磁通量也增大；根据楞次定律，线圈 B 中感应电流的磁场方向应该与原磁场方向相反，即如图中的虚线所示；再用右手螺旋定则判断感应电流的方向便可确定流过灵敏电流计的电流方向是 D → C。

 

37．如图所示，导线框 abcd 处在匀强磁场中，匀强磁场的方向垂直于导线框平面，与导线框接触良好的导体棒 MN 在外力作用下向右做匀速运动。试用楞次定律判断导体棒 MN 中感应电流的方向。

【答案】

N → M

【解析】

分析：通过判断通过闭合回路 MbcNM 的磁通量的变化，依据楞次定律来确定感应电流的方向。

解：当导体棒 MN 向右运动时，闭合回路 MbcNM 面积减小，通过的磁通量下降。根据楞次定律，感应电流产生的磁场跟原磁场同方向，以阻碍原磁通量的减少；用右手螺旋定则可知通过导体棒的感应电流方向是 N → M。

 

38．如图所示，一个闭合导体圆环 a 和有缺口的导体圆环 b 用细杆连接，可绕细杆中央的光滑转动轴 O 在水平面内自由转动。用足够强的条形磁体的任一极插入环 a 时，可观察到环向后退；插入 b 环时，环不动。试解释观察到的现象。

【答案】

条形磁体的任一极插入 a 环时，穿过 a 环的磁通量增加，根据楞次定律 a 环中感应电流的磁场阻碍原磁通量增大，环中感应电流的磁场和原条形磁体的磁场方向相反，所以条形磁体和存在感应电流的 a 环间的相互作用力是斥力，正如同名磁极相互排斥。而 b 环有缺口，条形磁体插入时，环中并无感应电流，和条形磁体间没有作用力，所以条形磁体插入 b 环时环不动。

【解析】

命题意图：强化科学思维推理、论证能力和归纳能力。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅱ）。

 

39．现将电池组、滑动变阻器、带铁芯的线圈 A、线圈 B、电流计及开关用导线按如图所示连接。在开关闭合、线圈 A 放在线圈 B 中的情况下，某同学发现将滑动变阻器的滑片 P 向左加速滑动时，灵敏电流计指针向右偏转。由此判断下列后续操作是否符合实验事实，简述判断的理由。

（1）线圈 A 向上拔出或滑动变阻器滑片 P 向右加速滑动，都能引起电流计指针向左偏转；

（2）线圈 A 中铁芯向上拔出或断开开关，都能引起电流计指针向右偏转；

（3）滑动变阻器的滑片 P 匀速向左或匀速向右滑动，都能使灵敏电流计指针静止在中央。

【答案】

已知滑动变阻器的滑动端 P 向左加速滑动时，滑动变阻器的电阻迅速增大，通过线圈 A 的电流迅速减小，通过线圈 B 的磁通量迅速减小，灵敏电流计的指针向右偏转。

（1）当线圈 A 向上拔出，通过线圈 B 的磁通量减小，灵敏电流计指针应向右偏转。此判断错。

滑动变阻器滑动端 P 向右加速滑动，滑动变阻器的电阻减小，通过线圈 A 的电流增大，通过线圈 B 的磁通量增大，灵敏电流计指针向左偏转。此判断对。

（2）对。两种操作均使通过线圈 B 的磁通量减小，电流计指针应该向右偏转。

（3）错。滑动变阻器的滑动端 P 匀速向左（或匀速向右）滑动，滑动变阻器的电阻均匀增大（或均匀减小），通过线圈 A 的电流均匀减小（或均匀增大），通过线圈 B 的磁通量均匀减小（或均匀增大），线圈 B 中产生感应电流，电流计指针不应静止，而应向右（或向左）偏转。

【解析】

命题意图：从不同的实验操作中归纳总结磁通量变化和感应电流方向之间的内在关联。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

40．如图所示，在 y 轴左侧有一垂直于纸面向里的匀强磁场，一个圆形线圈的一半放在磁场中，圆心与原点 O 重合，线圈平面与磁场方向垂直。若要使线圈中产生顺时针方向的感应电流，原磁场的磁通量应增大还是减少？感应电流磁场的方向如何？若使上述线圈中的感应电流为顺时针方向，线圈的运动方式有哪三种可能？

【答案】

原磁场的方向垂直于纸面向里，则顺时针方向感应电流产生的磁场方向也为垂直于纸面向里，根据楞次定律可知：线圈内原来的磁通量一定减少。

线圈沿 x 轴正方向移动，或线圈绕 x 轴转动且转角小于 90°，或线圈绕 y 轴转动且转角小于 90°，（或线圈绕 Oxy 平面内任意轴转动且转角小于 90° 均可）。上述这些可能的运动方式都能使线圈内原来的磁通量减少，则线圈中一定会产生顺时针方向的感应电流。

【解析】

命题意图：此题需要综合应用右手螺旋定则、楞次定律以及匀强磁场中磁通量的定义，要求学生具有一定的空间想象能力。此题也可以根据感应电流的方向应用“右手定则”判断线圈运动方向，但分析过程比较复杂。

主要素养与水平：模型建构（Ⅰ）；科学论证（Ⅱ）。

 

41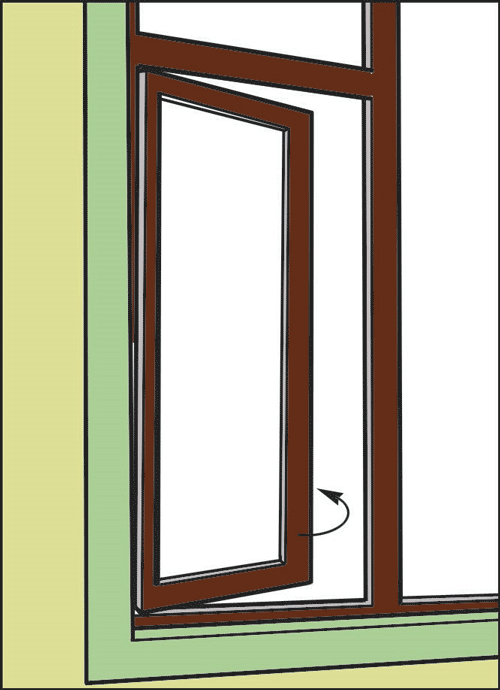．如图所示，某教室墙上有一朝南的钢窗，从室内学生的角度看，穿过窗户的地磁场是什么方向？学生推开窗户时，穿过窗户的地磁场的磁通量如何变化？从学生的角度看，窗框中的感应电流沿什么方向？

【答案】

从室内学生的角度看，穿过窗户的地磁场方向是指向窗内偏下，推窗过程中穿过窗户的地磁场的磁通量减小。根据楞次定律窗框中感应电流是逆时针方向。

【解析】

命题意图：在三维立体空间的具体情境中分析电磁感应现象，需要一定的模型建构能力和科学推理能力。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学论证（Ⅱ）。

 

42．如图所示，闭合铜环与闭合金属框相接触置于匀强磁场中。当铜环向右移动时（金属框不动）：甲同学认为闭合铜环 egfhe 的磁通量没有发生变化，所以闭合铜环内没有感应电流；乙同学认为闭合回路 eadfge 的磁通量变大，根据楞次定律有逆时针方向的感应电流。请根据所学知识判断甲、乙两同学的观点是否正确，并简述理由。

【答案】

甲同学的观点错误，乙同学的观点正确。如果没有金属框，单独铜环向右移动的过程中，闭合铜环 egfhe 的磁通量没有发生变化，所以闭合铜环内没有感应电流。当铜环在闭合金属框上向右移动时，虽然闭合回路 egfhe 内的磁通量没有变化，但与之相联系的回路 eadfge 和回路 ebcfhe 的磁通量却同时发生变化。因此，回路中有感应电流产生。电流方向可以根据楞次定律判断（回路 eadfge 的磁通量在逐渐增加，将有逆时针方向的感应电流；回路 ebcfhe 磁通量在逐渐减小，将有顺时针方向的感应电流）。因此铜环的左右两侧分别存在 f→g→e 和 f→h→e 方向的感应电流。

应用“右手定则”也可以判断感应电流的方向，注意切割磁感线的等效长度为圆 egfhe 的直径。

【解析】

命题意图：灵活确定研究对象的磁通量变化规律，为第 3 节应用法拉第电磁感应定律解决问题做准备。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅲ）。

 

43．如图所示，AOC 是光滑的直角金属导轨，AO 沿竖直方向，OC 沿水平方向。ab 为靠在导轨上的一根金属直棒，b 端较 a 端更靠近 O 点。金属直棒从静止开始在重力作用下运动，运动过程中 b 端始终在 OC 上，a 端始终在 AO 上，直到金属直棒 ab 完全落在 OC 上。整个装置放在一匀强磁场中，磁场方向垂直纸面向里。则：

（1）确定金属直棒 ab 在运动过程中感应电流的方向，并说明判断的理由；

（2）确定金属直棒 ab 所受磁场力的方向，并说明判断的理由。

【答案】

（1）金属直棒中感应电流方向先是 b→a，后变为 a→b。

当 ab 棒在图示位置运动到倾角为 45° 的过程中，ab 棒与直角金属导轨包围的面积增大，磁通量也增大，根据楞次定律感应电流的磁场要反抗磁通量的增大，在 ab 棒与直角金属导轨组成的回路中产生逆时针方向的感应电流，所以通过 ab 棒的感应电流方向是 b→a；当 ab 棒继续运动的过程中，ab 棒与直角金属导轨包围的面积减小，磁通量也减小，根据楞次定律感应电流的磁场要反抗磁通量的减小，在 ab 棒与直角金属导轨组成的回路中产生顺时针方向的感应电流，所以通过 ab 棒的感应电流是 a→b。

（2）金属直棒中感应电流方向为 b→a 时，根据“左手定则”判断磁场力方向与 ab 垂直指向左下方向；当金属直棒中感应电流方向为 a→b 时，磁场力方向与 ab 垂直指向右上方向。

【解析】

命题意图：楞次定律结合“左手定则”判断感应电流的方向和安培力的方向，关注磁通量变化问题中可能出现磁通量的极大值。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅲ）；科学推理（Ⅲ）。

 

44．一螺线管的匝数 n = 400、截面积 S = 0.20 m²，其内部存在向左的匀强磁场，磁感应强度 B 逐渐增加且均匀变化，如图 6–18 所示。设磁感应强度的变化率 \(\frac{{\Delta B}}{{\Delta t}}\) = 0.10 T/s，电阻 R 为 10 Ω，忽略螺线管导线的电阻，试求：

（1）螺线管内感应电动势的大小和通过电阻 R 的感应电流方向；

（2）在 Δt = 2.0 s 时间内通过电阻 R 的感应电荷量。

【答案】

（1） E = 8.0 V

通过电阻 R 的感应电流方向 c → d。

（2）q = 1.6 C

【解析】

分析：根据法拉第电磁感应定律可以求螺线管内产生的感应电动势大小，根据楞次定律可以判断感应电流的方向，再通过电流和电荷量的关系求出通过电阻的感应电荷量。

解：（1） 由于螺线管内磁场的磁感应强度均匀变化，根据法拉第电磁感应定律，螺线管内感应电动势

E = n\(\frac{{\Delta \Phi }}{{\Delta t}}\)

                                                                     = nS\(\frac{{\Delta B }}{{\Delta t}}\)

                                                                     = 400×0.20×0.10 V

                                                                     = 8.0 V

根据楞次定律，通电螺线管感应电流的磁场阻碍原磁场的变化，从而可以判断通过电阻 R 的感应电流方向 c → d。

（2）螺线管内感应电流的大小

I = \(\frac{E}{R}\) = \(\frac{{8.0}}{{10}}\) A = 0.80 A

则在 2.0 s 时间内，通过电阻 R 的感应电荷量

q = IΔt = 0.80 × 2.0 C = 1.6 C

 

45．如图所示，在一个磁感应强度 B = 0.5 T 的匀强磁场中，垂直于磁场方向水平放置两根相距为 l = 0.1 m 的平行光滑金属导轨 MN 和 PQ，导轨电阻忽略不计；在两根导轨的端点 N、Q 之间连接一个阻值 R = 0.3 Ω 的电阻；垂直于导轨放置一根与导轨接触良好的金属棒，金属棒在接触点 a、b 之间部分的电阻 r = 0.2 Ω。若金属棒在水平拉力 F 作用下以速度 v = 4.0 m/s 向右做匀速运动，试求：

（1）通过电阻 R 的电流大小和方向；

（2）使金属棒做匀速运动的拉力；

（3）回路中的热功率。

【答案】

（1）I = 0.4 A

电流的方向为从 Q 经 R 到 N。

（2）F = 0.02 N

（3）P_Q = 0.08 W

【解析】

分析：金属棒在水平拉力 F 作用下向右匀速运动垂直切割磁感线，在金属棒中产生了感应电动势。以金属棒为研究对象，根据“右手定则”判断感应电流的方向是 a → b。金属棒和电阻 R 组成的闭合回路中金属棒 ab 部分相当于一个电源。金属棒的电阻相当于这个闭合电路的内阻，外电路的电阻为 R。根据“左手定则”通有感应电流的金属棒在磁场中受到向左的安培力的作用，要保持金属棒匀速运动必定受到向右的水平拉力 F 作用，且水平拉力 F 的大小等于安培力的大小。

解：根据法拉第电磁感应定律，金属棒垂直切割磁感线产生感应电动势为 E_ab = Blv，在金属棒和电阻 R 组成的闭合电路中内阻 r = 0.2 Ω，外电阻 R = 0.3 Ω。

（1）根据闭合电路欧姆定律，通过电阻 R 的电流也就是通过金属棒的电流，电流的大小

I = \(\frac{{{E_{ab}}}}{{R + r}}\) =  \(\frac{{Blv}}{{R + r}}\) = \(\frac{{0.5 \times 0.1 \times 4.0}}{{0.3 + 0.2}}\) A = 0.4 A

电流的方向为从 Q 经 R 到 N。

（2）由于金属棒做匀速运动，金属棒受到安培力的方向向左，外力 F 的方向向右。安培力与外力是一对平衡力，外力 F 的大小

F = F _安 = BIl = 0.5×0.4×0.1 N = 0.02 N

（3）根据焦耳定律，回路中电流的热功率

P_Q = I²（R + r） = 0.4²×（0.3 + 0.2）W = 0.08 W

 

46．如图所示，边长分别为 l 与 h、电阻为 R、质量为 m 的金属线框，自上而下匀速穿过宽度为 h、磁感应强度为 B 的匀强磁场区域。求在这个过程中线框产生的热量。

【答案】

Q = 2mgh

【解析】

分析：线框匀速穿过匀强磁场的过程可分为两段：

（1）线框刚进入磁场到全部进入磁场，cd 边切割磁感线，根据楞次定律，线框中的感应电流是逆时针方向，根据“左手定则”，由于感应电流，cd 边受到的安培力方向为竖直向上；

（2）线框从磁场中离开，ab 边切割磁感线。线框中的感应电流是顺时针方向，ab 边受到的安培力方向仍然是竖直向上。

其实，根据楞次定律，感应电流总是起到“阻碍”线框下落的作用。现在线框下落，无论是线框的 ab 边还是 cd 边处于磁场范围内，“阻碍”作用必然表现为线框受到向上的阻力作用，即由于感应电流，ab 边或 cd 边受到的安培力总是向上。感应电流做功使机械能转变成内能。

解：线框在穿过磁场区域过程中，只有一条边切割磁感线，线框中产生的感应电动势 E 与感应电流大小始终不变。以线框为研究对象，线框所受重力方向竖直向下，安培力方向始终竖直向上。因为线框做匀速直线运动，所以线框所受重力和安培力是一对平衡力，即

\[mg = BIl\]

其中 I = \(\frac{E}{R}\) = \(\frac{{Blv}}{R}\)，得

\[{mg = B\frac{{Blv}}{R}l}\]                                   ①

\[ = \frac{{{ B^2}{l^2}v}}{R} \]

线框进入磁场和离开磁场都做匀速直线运动，所用时间均为 t = \(\frac{h}{v}\)。

电流做的总功

\[\begin{array}{l}W = 2{I^2}Rt\\ = 2\frac{{{B^2}{l^2}vh}}{R}\end{array}\]

可知线框产生的热量

\[{Q = W = 2\frac{{{B^2}{l^2}vh}}{R}}\]                                    ②

将①式代入②式得

\[Q = 2mgh\]

还可以换一个思路考虑。因为线框下落过程中速度不变，即线框的动能不变，所以线框产生的热量是由重力势能转变成电能再转变而来的。在线框通过磁场的过程中，重力势能减少了 2mgh，根据能量守恒定律线框产生的热量 Q 一定等于 2mgh。

由此例可知，在解决与电磁感应相关的实际问题时，有时用能量守恒定律可以相当简单快捷。

 

47．在涉及磁通量、磁通量的变化率以及感应电动势的概念时，试列举符合以下说法的实例。

（1）磁通量增大，磁通量的变化率减小。

（2）磁通量为零，磁通量的变化率不为零。

（3）磁通量减小，感应电动势增大。

（4）磁通量减小，感应电动势减小。

【答案】

（1）闭合线圈垂直于磁场方向，磁感应强度逐渐增大，通过线圈的磁通量也增大，但单位时间内磁感应强度的增加量变小，通过线圈磁通量的增加量也变小，即磁通量的变化率减小，如图中曲线（1）所示

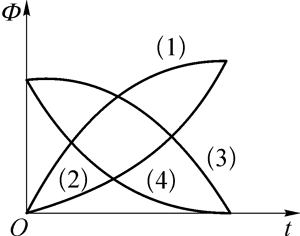
（2）闭合线圈垂直于磁场方向，磁感应强度为零，通过线圈磁通量也为零。磁感应强度从零开始增大，单位时间内通过线圈的磁通量也增大，即通过线圈的磁通量的变化率不为零，如图 1 中曲线（2）所示，t = 0 时刻，磁通量为零，磁通量的变化率不为零。

（3）闭合线圈垂直于磁场方向，磁感应强度逐渐减小，通过线圈的磁通量也逐渐减小，但单位时间内磁感应强度的减小量变大，即通过线圈的磁通量的变化率变大，根据法拉第电磁感应定律，感应电动势一定增大，如图 1 中曲线（3）所示。

（4）闭合线圈垂直于磁场方向，磁感应强度逐渐减小，通过线圈的磁通量也逐渐减小，但单位时间内磁感应强度的减小量变小，即通过线圈的磁通量的变化率变小，根据法拉第电磁感应定律，感应电动势一定减小，如图 1 中 曲线图（4）所示。

【解析】

命题意图：理解磁通量、磁通量的变化量、磁通量的变化率和感应电动势的物理意义。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅲ）。

 

48．边长为 0.1 m 的 200 匝正方形线圈处在匀强磁场中，匀强磁场垂直穿过正方形线圈。磁感应强度 B 随时间 t 的变化规律如图（a）所示，在图（b）、（c）中分别画出磁通量 Φ 和感应电动势 E 随时间 t 的变化规律。

【答案】

因为 \(\frac{{\Delta \Phi }}{{\Delta t}}\) = S \(\frac{{\Delta B}}{{\Delta t}}\) = a² \(\frac{{\Delta B}}{{\Delta t}}\) = 0.1² \(\frac{{\Delta B}}{{\Delta t}}\) = 0.01 \(\frac{{\Delta B}}{{\Delta t}}\)，所以磁通量随时间的变化趋势与磁感应强度随时间的变化趋势相同，但两者的单位和大小均不同，Φ – t 图像如图（a）所示。

在 0 ~ 2 s 内，感应电动势为负值，大小为 E₁ = n \(\frac{{\Delta {\Phi _1 }}}{{\Delta t}}\) = nS \(\frac{{\Delta {B_1}}}{{\Delta t}}\) = na² \(\frac{{\Delta {B_1}}}{{\Delta t}}\) = 200×0.1²×\(\frac{2}{2}\) V = 2 V。

在 2 ~ 4 s 内，感应电动势为正值，大小为 E₂ = n \(\frac{{\Delta {\Phi _2}}}{{\Delta t}}\) = nS \(\frac{{\Delta {B_2}}}{{\Delta t}}\) = na² \(\frac{{\Delta {B_2}}}{{\Delta t}}\) = 200×0.1²×\(\frac{{2 - ( - 2)}}{2}\) V = 4 V。

在 4 ~ 6 s 内，感应电动势为负值，大小 E₃ = E₁。E – t 图像如图（b）所示。

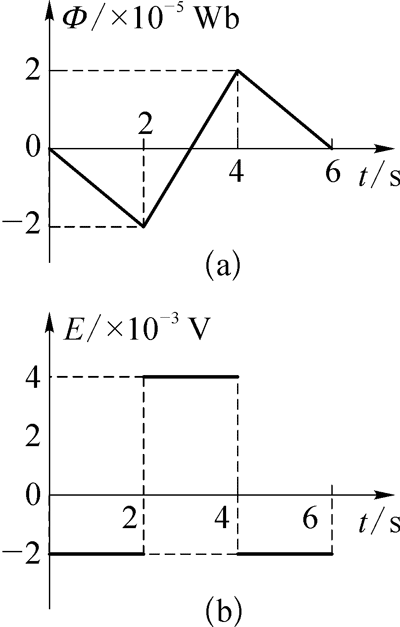
【解析】

命题意图：理解图像所表示的磁通量的变化量、磁通量的变化率和感应电动势。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅲ）；科学推理（Ⅲ）。

 

49．如图所示，边长为 L 的正方形导线框 abcd 放在纸面内，在 ad 边左侧有足够大的匀强磁场，磁感应强度大小为 B，方向垂直纸面向里，使导线框绕过 a 点垂直于纸面的轴在纸面内顺时针转动，经时间 Δt 转到图中虚线位置。试求时间 Δt 内导线框 abcd 中感应电流的方向和平均感应电动势的大小。

【答案】

导线框内磁通量减小，根据楞次定律感应电流的方向为顺时针方向；

\(\bar E\) = \(\frac{{\Delta \Phi }}{{\Delta t}}\) = \(\frac{{B{L^2} - \frac{1}{2}B{L^2}}}{{\Delta t}}\) = \(\frac{{B{L^2}}}{{2\Delta t}}\)

【解析】

命题意图：理解在匀强磁场中线圈包围磁场有效面积变化计算磁通量的变化率，进而计算感应电动势。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

50．如图（a）所示，阻值为 R、匝数为 n 的圆形金属线圈与一个阻值为 2R 的电阻连接成闭合电路；线圈的半径为 r₁，在线圈中有一个半径为 r₂ 的圆形匀强磁场区域，该磁场方向垂直于线圈平面。磁感应强度 B（向里为正）随时间 t 变化的关系如图（b）所示，图中 B₁、t₁ 为已知量。导线电阻不计。

判断 t₁ 时刻通过电阻的电流方向和大小，并说明判断的理由。

【答案】

线圈内磁感应强度减小，根据楞次定律感应电流的磁场方向与原磁场方向相同，由右 手螺旋定则可知线圈中感应电流的方向为顺时针方向，所以通过电阻的电流方向为 b→a。

根据法拉第电磁感应定律，感应电动势为

E = n \(\frac{{\Delta \Phi }}{{\Delta t}}\) = nπr₂² \(\frac{{\Delta B}}{{\Delta t}}\) = nπr₂² \(\frac{{{B_1}}}{{{t_1}}}\)  = \(\frac{{n\pi r_2^2{B_1}}}{{{t_1}}}\)

根据闭合电路欧姆定律，感应电流为

I = \(\frac{E}{{R + 2R}}\) = \(\frac{{\frac{{n\pi r_2^2{B_1}}}{{{t_1}}}}}{{3R}}\) = \(\frac{{n\pi r_2^2{B_1}}}{{3{t_1}R}}\)

【解析】

命题意图：计算由磁感应强度发生变化引起的多匝线圈的感应电动势，结合闭合电路欧姆定律计算感应电流。理解公式中的“面积”不是线圈的截面积，而是线圈包围磁场的面积。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

51．如图所示，一个“∠”形导轨垂直于磁场固定在磁感应强度为 B 的匀强磁场中，ab 是与导轨材料相同的导体棒，导体棒与导轨接触良好。在外力作用下，导体棒以恒定速度 v 向右运动。若以导体棒处于图示位置的时刻作为计时起点，在图中画出回路中感应电动势 E、感应电流 I、导体棒所受外力的功率 P 和回路中产生的焦耳热 Q 随时间变化的图像。

【答案】

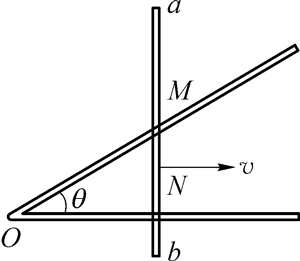如图所示，导体棒与导轨接触点为 M 和N，“∠”型导轨的夹角为 θ，导体棒与导轨单位长度的电阻为 λ。则经过时间 t，导体棒和导轨之间的距离为 ON = vt，导体棒切割磁感线的长度为 MN = vt tanθ，倾斜部分导轨的长度为 OM = \(\frac{{vt}}{{\cos \theta }}\)。

感应电动势为        E = B（vt tanθ）v = （Bv² tanθ）t

感应电流为             I = \(\frac{E}{R}\) = \(\frac{{(B{v^2}\tan \theta )t}}{{\lambda (vt + vt\tan \theta  + \frac{{vt}}{{\cos \theta }})}}\) = \(\frac{{Bv\tan \theta }}{{\lambda (1 + \tan \theta  + \frac{1}{{\cos \theta }})}}\)

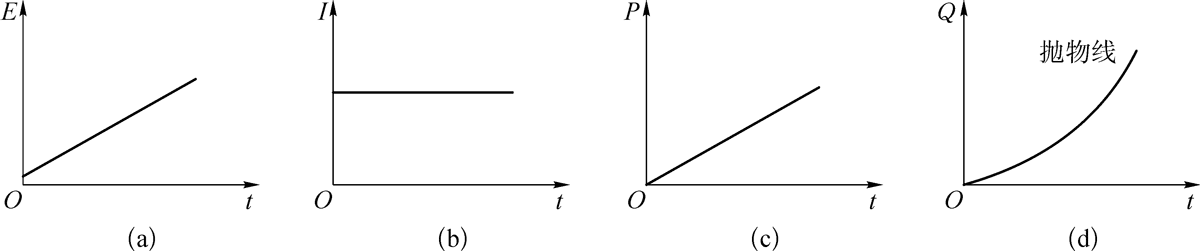
外力的功率为        P = P_电 = EI = （Bv² tanθ）t \(\frac{{Bv\tan \theta }}{{\lambda (1 + \tan \theta  + \frac{1}{{\cos \theta }})}}\) = \(\frac{{{ B^2}{v^3}{{\tan }^2}\theta }}{{\lambda (1 + \tan \theta  + \frac{1}{{\cos \theta }})}}\) t

回路中产生的焦耳热为        Q = I²Rt = P_电t = \(\frac{{{B^2}{v^3}{{\tan }^2}\theta }}{{\lambda (1 + \tan \theta  + \frac{1}{{\cos \theta }})}}\) t²

下图为感应电动势、感应电流、外力的功率和回路中产生的焦耳热随时间变化的关系

 4

【解析】

命题意图：理解导体切割磁感线产生感应电动势的相关概念，结合闭合电路欧姆定律分析电流、电功率和焦耳热随时间的变化规律。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

52．如图所示，虚线框内为磁感应强度 B 为 1.0 T 的匀强磁场区域，磁场方向垂直纸面向外；在水平向右的外力作用下，一个边长为 0.20 m 的正方形闭合导线框 abcd 沿纸面以 0.10 m/s 的速度由左向右匀速进入磁场。导线框每条边的电阻均为 1.0 Ω，dc 边相当于“电源”。用电池等符号画出正方形闭合导线框的等效电路图，图中标注电流的方向，并计算：

（1）在导线框进入磁场过程中 ad 边受到的安培力随时间变化的关系；

（2）导线框进入磁场过程中感应电流产生的焦耳热；

（3）导线框进入磁场过程中通过导线的电荷量。

【答案】

（1）导线框的边长为 a = 0.20 m，其 dc 边刚进入磁场时产生感应电动势为

E = Bav = 1.0×0.20×0.10 V = 0.020 V

等效电路图为

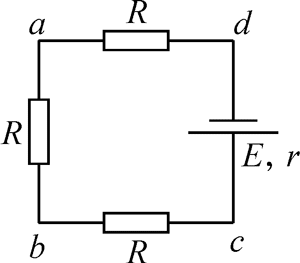
导线框每条边的电阻 R = r = 1.0 Ω。感应电流大小为

I = \(\frac{E}{{3R + r}}\) = \(\frac{{0.020}}{{3 \times 1.0 + 1.0}}\) A = 5.0×10⁻³ A= 5.0 mA

感应电流的方向为 adcba。

在导线框进入磁场过程中 ad 边受到的安培力

F_Aab = BI(a − vt) = 1.0×5.0×10⁻³×(0.20 – 0.10t）N = (1.0×10⁻³ – 5.0×10⁻⁴t）N

（2）导线框进入磁场过程中感应电流产生的焦耳热

Q = I²(3R + r)t = I²(3R + r) \(\frac{a}{v}\) = (5.0×10⁻³)²(3×1.0 + 1.0)×\(\frac{{0.20}}{{0.10}}\) J = 2.0×10⁻⁴ J

（3）导线框进入磁场过程中通过导线的电量

q = It = I \(\frac{a}{v}\) = 5.0×10⁻³×\(\frac{{0.20}}{{0.10}}\) C = 1.0×10⁻² C

【解析】

命题意图：计算由磁感应强度发生变化引起的感应电动势，综合应用闭合电路欧姆定律计算感应电流、焦耳热和电量，提高科学思维素养。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅲ）。

 

53．如图所示，光滑竖直平行导轨上套有一质量为 m 的导体棒 ab，导轨上端连接一阻值为 R 的电阻，导体棒 ab 的电阻阻值为 \(\frac{R}{2}\)，其余电阻不计。现导体棒 ab 自由下落，以速度 v 进入高为 h 的水平匀强磁场区域，穿出磁场时的速度为 \(\frac{v}{2}\)。则导体棒 ab 穿过磁场区域过程中产生多少焦耳热？电阻 R 产生多少焦耳热？

【答案】

导体棒 ab 穿过磁场区域过程中，受到竖直向下的重力和竖直向上的安培力作用，应用动能定理，得

mgh − W_安 = \(\frac{1}{2}\) m (\(\frac{1}{2}\))² − \(\frac{1}{2}\) mv²

导体棒穿过磁场区域过程中产生的焦耳热

Q_总 = W_安 = mgh + \(\frac{3}{8}\) mv²

已知导体棒的电阻为 r = \(\frac{R}{2}\)，则

Q_总 = \({\bar I}\)²(R + r)t

Q_R = \({\bar I}\)²Rt

电阻 R 产生的焦耳热

Q_R = \(\frac{R}{R+r}\) Q_总 = \(\frac{2}{3}\) Q_总 = \(\frac{2}{3}\) mgh + \(\frac{1}{4}\) mv²

【解析】

命题意图：根据电磁感应现象中的能量转化和守恒关系分析解决实际问题，应用动能定理和焦耳定律分析和计算，提高能量观念和科学思维素养。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

54．如图所示，一长直铁芯上绕有一固定线圈 M，铁芯右端与一木质圆柱连接，木质圆柱上套有一闭合金属环 N，N 可在木质圆柱上无摩擦移动，R 为滑动变阻器，E₁ 和 E₂ 为直流电源，S 为单刀双掷开关。则：

（1）在 S 断开的情况下，S 向 a 闭合的瞬间金属环 N 向木质圆柱的哪一端运动？

（2）在 S 断开的情况下，S 向 b 闭合的瞬间金属环 N 向木质圆柱的哪一端运动？

（3）在 S 已向 a 闭合的情况下，将 R 的滑片向 c 端移动时，金属环 N 向木质圆柱的哪一端运动？

（4）在 S 已向 a 闭合的情况下，将 R 的滑片向 d 端移动时，金属环 N 向木质圆柱的哪一端运动？

【答案】

由楞次定律金属环 N 的运动趋势或运动总是阻碍通过金属环的磁通量的变化，只要金属环 N 的磁通量增大就向右运动；金属环 N 的磁通量减小就向左移动。

（1）在 S 断开的情况下，S 向 a 闭合的瞬间，通过金属环 N 的磁通量增大，金属环向右运动。

（2）在 S 断开的情况下，S 向 b 闭合的瞬间，通过金属环 N 的磁通量增大，金属环向右运动。

（3）在 S 已向 a 闭合的情况下，将 R 的滑片向 c 端移动时电阻阻值增大，通过线圈的电流减小，通过金属环 N 的磁通量减小，金属环向左运动。

（4）在 S 已向 a 闭合的情况下，将 R 的滑片向 d 端移动时电阻阻值减小，通过线圈的电流增大，通过金属环 N 的磁通量增大，金属环向右运动。

【解析】

命题意图：用楞次定律分析产生感应电流的方向，再用“左手定则判断金属环运动的方向”，或者根据楞次定律内在本质，根据磁通量变化趋势直接判断金属环的运动方向。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

55．扫描隧道显微镜（STM）可用来探测样品表面原子尺寸上的形貌。为了有效隔离外界震动对 STM 的扰动，在圆底盘周边沿其径向对称地安装若干对紫铜薄板，并施加磁场来快速衰减其微小震动，如右图所示。如下图所示是对紫铜薄板施加恒定磁场的四种方案。试问出现扰动时，对于紫铜薄板上下、左右震动衰减最有效的方案是哪一个？说明判断的理由。

【答案】

（a）感应电流产生的条件是闭合回路中的磁通量发生变化。系统左右或上下震动时紫铜薄板在磁场中的部分有时多有时少，磁通量发生变化能产生感应电流，感应电流在磁场中受到安培力能够阻碍系统的震动，故图（a）正确；图（d）能阻碍系统左右震动，但不能阻碍系统上下震动，图（b）和（c）均不能阻碍系统左右震动或上下震动，故图（b）、（c）和（d）均错。

【解析】

命题意图：将实际问题中的对象转换成物理模型，通过分析获得结论，提高科学思维素养。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）；科学论证（Ⅱ）；科学本质（Ⅰ）。

 

56．如图所示，虚线框内存在匀强磁场，磁场方向垂直于纸面向里，粗细均匀的电阻丝围成的正方形线框置于匀强磁场中，正方形线框的边与虚线框平行。线框以同样大小的速度沿四个不同方向平移出磁场，则在正方形线移出的过程中，线框的一边 a、b 两点间电势差的绝对值 U_ab 分别为多大？

【答案】

正方形线框四种运动中均有一条边切割磁感线，产生的感应电动势和感应电流均相同。设线框每条边的电阻为 R，感应电流为 I，图（a）中 U_ab = IR；图（b）中 U_ab = I（3R）= 3IR；图（c）和图（d）中同为U_ab = IR。

【解析】

命题意图：通过分析线框在四种不同运动情况中发生电磁感应现象所涉及的相同物理量和不同物理量，有助于提高科学思维素养。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

57．一单匝线圈在匀强磁场中绕垂直于磁场的轴匀速转动时，穿过线圈的磁通量随时间的变化关系如图所示。则在 0 ~ 2 s 内线圈中感应电动势随时间如何变化？ 0 ~ 2 s 内线圈中感应电动势的平均值多大？

【答案】

0 ~ 1 s 内线圈中感应电动势从 0 逐渐增大，1 s 末最大，1 ~ 2 s 内线圈中感应电动势从最大逐渐减小到 0。

0 ~ 2 s 内线圈中感应电动势的平均值为

\[\bar E = \frac{{\Delta \Phi }}{{\Delta t}} = \frac{{|{\Phi _2} - {\Phi _1}|}}{{\Delta t}} = \frac{{| - 2.0 \times {{10}^{ - 3}} - 2 \times {{10}^{ - 3}}|}}{2}\;{\rm{V}} = 2.0 \times {10^{ - 3}}\;{\rm{V}}\]

【解析】

命题意图：从磁通量随时间变化的图像中分析感应电动势的大小。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅳ） 。

 

58．如图所示，abcd 是光滑水平放置的金属框，PQ 为导体棒，静止在框架上；一条形磁体绕金属框平面内的 OO′ 轴转过 90°。在此过程中，闭合回路 QPbc 内磁通量如何变化？导体棒将如何运动？条形磁体的转动方向与导体棒的运动方向有没有关系？说明判断的理由。

【答案】

闭合回路 QPbc 内磁通量增大，导体棒将向右运动。

条形磁体的转动方向与导体棒的运动方向之间没有关系。无论条形磁体绕轴 OO′ 向哪个方向转动，在导体棒与金属框组成的闭合回路 QPbc 内的磁通量均增大，根据楞次定律知其感应电流的磁场均要反抗磁通量的增大。由于在条形磁体中部垂直于磁体轴线的闭合回路面积越小磁通量越大，闭合回路面积越大磁通量越小，所以导体棒 QP 必然向右运动。

【解析】

命题意图：深刻理解楞次定律的物理意义，根据条形磁体的磁场分布特点，灵活应用楞次定律解决具体问题。

主要素养与水平：运动与相互作用（Ⅲ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

59．如图所示，匀强磁场中有一个用软导线制成的单匝闭合线圈，线圈平面与磁场垂直。已知线圈的面积为 S、电阻为 R，磁场的磁感应强度为 B。现同时向两侧拉动线圈，线圈的两边在 Δt 时间内合到一起。则线圈在上述过程中感应电动势的平均值多大？感应电流的平均值多大？感应电流的方向如何？通过导线横截面的电荷量多大？

【答案】

平均感应电动势为 \(\bar E = \frac{{\Delta \Phi }}{{\Delta t}} = \frac{{BS}}{{\Delta t}}\)

平均电流为 \(\bar I = \frac{{\bar E}}{R} = \frac{{BS}}{{R\Delta t}}\)，感应电流的方向为顺时针，通过导线横截面的电量为

\[q = \bar I\Delta t = \frac{{\Delta \Phi }}{{\Delta t}}\frac{{\Delta t}}{R} = \frac{{\Delta \Phi }}{R} = \frac{{BS}}{R}\]

【解析】

命题意图：通过计算由于匀强磁场中导线所围成“面积”的变化而产生的感应电动势，加深对相关概念的理解。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅳ）。

 

60．一根长 50 cm 的直导线在磁感应强度为 0.20 T 的匀强磁场中向垂直于磁场的方向匀速运动。如果导线中的感应电动势为 1.0 V，直导线的运动速度多大？如果该直导线连接成的回路总电阻为 2.0 Ω，沿着直导线运动速度方向的拉力为多大？

【答案】

根据法拉第电磁感应定律 E = Blv，直导线的运动速度为

\[v = \frac{E}{{Bl}} = \frac{{1.0}}{{0.20 \times 0.50}}\;{\rm{m/s}} = 10\;{\rm{m/}}\]

通过直导线的电流为 I = \(\frac{E}{R}\) = \(\frac{1.0}{2.0}\) A = 0.50 A，拉力为

F = F_A = BIl = 0.20×0.50×0.50 N = 0.050 N

【解析】

命题意图：导线匀速且垂直切割磁感线产生感应电动势，此时外力大小等于安培力。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

61．如图所示，由导体组成半径为 r 的水平圆环内有垂直于纸面向里、磁感应强度为 B 的匀强磁场，电路的固定电阻为 R，线框其余电阻不计，一根长度大于 2r、电阻不计的导体棒 MN 以速度 v 在圆环上自左端向右端无摩擦地匀速滑动。试求 MN 从左端滑到右端的过程中，通过电阻 R 的电流平均值及通过电阻 R 的电荷量。

【答案】

\[\bar I = \frac{E}{R} = \frac{1}{R} \times \frac{{\Delta \Phi }}{{\Delta t}} = \frac{{B\pi {r^2}}}{{R\Delta t}} = \frac{{B\pi rv}}{{2R}}\]

\[q = \bar I\Delta t = \frac{{B\pi {r^2}}}{R}\]

【解析】

命题意图：理解导体棒垂直切割磁感线产生感应电动势，提高结合闭合电路欧姆定律分析实际问题的能力。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

62．如图所示，有两根和竖直方向成 α 角的光滑平行的金属轨道，上端接有可变电阻 R、下端足够长，空间有垂直于轨道平面磁感应强度为 B 的匀强磁场，一根长为 L（与金属轨道间距近似相等）、质量为 m 的金属杆从轨道上端由静止开始滑下，金属杆与轨道接触良好，且金属杆的运动方向始终与杆垂直，金属杆的电阻为 r。

（1）当金属杆速度为 v 时，求感应电动势、感应电流和金属杆受到的安培力。

（2）经过足够长的时间后，金属杆的速度会趋近于一个最大值。求最大速度 v_max。

【答案】

（1）E = BLv，I = \(\frac{E}{{R + r}}\) = \(\frac{{BLv}}{{R + r}}\)，F_A = BIL = \(\frac{{{B^2}{L^2}v}}{{R + r}}\)

（2）F_A = mgcosα，\(\frac{{{B^2}{L^2}{v_{\max }}}}{{R + r}}\) = mgcosα，v_max = \(\frac{{(R + r)mg\cos \alpha }}{{{B^2}{L^2}}}\)

【解析】

命题意图：理解在斜面上的金属杆垂直切割磁感线产生感应电动势，结合闭合电路欧姆定律和牛顿运动定律分析问题，理解速度趋近于最大值时金属杆处于平衡状态。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅳ）。

 

63．如图所示，用两根材料、粗细、长度完全相同的导线绕成匝数分别为 n₁ = 5 和 n₂ = 10 的圆形闭合线圈 a 和 b，两线圈处于同一平面并与匀强磁场垂直。当磁感应强度随时间均匀变化时，两线圈中的感应电动势之比 E_a∶E_b 为多大？感应电流之比 I_a∶I_b 为多大？

【答案】

设线圈半径为 r，匝数为 n；导线长度均为 L，截面积均为 S₀，电阻率均为 ρ，且  \(\frac{{\Delta B}}{{\Delta t}}\) = k。则 L = n（2πr），线圈中的感应电动势为

\[E = ns\frac{{\Delta B}}{{\Delta t}} = n(\pi {r^2})\frac{{\Delta B}}{{\Delta t}} = n\pi {\left( {\frac{L}{{2\pi n}}} \right)^2}k \propto \frac{1}{n}\]

所以 \(\frac{{{E_{\rm{A}}}}}{{{E_{\rm{B}}}}}\) = \(\frac{n_2}{n_1} \) = \(\frac{10}{5}\) = \(\frac{2}{1}\)，即感应电动势之比 E_A∶E_B = 2∶1

线圈中的感应电流为

\[I = \frac{E}{R} = \frac{E}{{\rho \frac{L}{{{S_0}}}}} \propto E\]

则 \(\frac{{{I_{\rm{A}}}}}{{{I_{\rm{B}}}}}\) = \(\frac{{{E_{\rm{A}}}}}{{{E_{\rm{B}}}}}\) = \(\frac{2}{1}\)，即感应电流之比 I_A∶I_B = 2∶1

【解析】

命题意图：理解 n 匝线圈内的磁感应强度变化产生感应电动势，结合欧姆定律和电阻定律分析相关物理量。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅳ）。

 

64．如图所示，在磁感应强度大小为 B、方向竖直向上的匀强磁场中，有一质量为 m、阻值为 R 的闭合矩形金属线框 abcd 用绝缘轻质细杆悬挂在 O 点，并可绕 O 点摆动，细杆和金属框处在同一平面内；金属线框从右侧某一静止位置开始释放。在摆动到左侧最高点的过程中，细杆和金属框共处的平面始终和纸面垂直。判断线框中感应电流的方向，说明判断的理由。

【答案】

线框中感应电流的方向是 adcba。

当金属线框从右侧某一位置静止释放，运动到最低点的过程中，穿过线框的磁通量减小，根据楞次定律感应电流的磁场方向与原磁场方向相同，感应电流的方向为 adcba。当金属线框从最低点运动到左侧最高点的过程中，穿过线框的磁通量增大，根据楞次定律感应电流的磁场方向与原磁场方向相反，由于穿过线框的磁通量方向相反，实际感应电流的方向仍为 adcba。

【解析】

命题意图：分析线框在三维空间运动过程中磁通量的变化，应用楞次定律判断感应电流的方向，说明判断的理由，这将有利于提高科学思维的素养和文字表述能力。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅲ）。

 

65．如图所示，两同心圆环 A、B 置于同一水平面上，其中 A 为均匀带电绝缘环，B 为导体环，两环均可绕垂直于纸面过圆心的轴在水平面内转动。若 A 匀速转动或加速转动，B 中有没有感应电流？感应电流的方向如何？说明判断的理由。

【答案】

若环 A 匀速转动，环 B 内产生稳定的磁场，环 B 内的磁通量不变，所以环 B 中没有感应电流。

若环 A 带正电荷，且顺时针加速转动（或逆时针减速转动），环 B 内产生垂直于纸面向里的磁场增大（或垂直于纸面向外的磁场减小），环 B 向里的磁通量增大（或向外的磁通量减小），根据楞次定律环 B 中的感应电流为逆时针方向；反之，若环 A 带负电荷，且环 A 顺时针加速转动（或逆时针减速转动），环 B 内产生垂直于纸面向外的磁场增大（或垂直于纸面向里的磁场减小），环 B 向外的磁通量增大（或向里的磁通量减小），根据楞次定律环 B 中的感应电流为顺时针方向。

环 A 带正电荷顺时针加速转动等效于带负电荷逆时针加速转动，环 A 带负电荷顺时针加速转动类似于带正电荷逆时针加速转动。

【解析】

命题意图：绝缘环可能带正、负两种的电荷，绝缘环的旋转方向和旋转快慢变化也可能不同，但是产生的感应电流只有顺时针和逆时针两种不同的方向。通过本题要求能够根据楞次定律分析实际现象过程中发现物理本质，归纳内在的物理规律，有助于提高对较复杂实际情景综合分析问题的能力，解决此类问题需要具有较高的科学思维素养。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅳ）。

 

66．如图所示，虚线框内存在垂直于纸面向里的匀强磁场，宽度为 L 的水平导线框 MNPQ 有一部分处在匀强磁场中。光滑导体棒与两根导轨接触良好，接触点分别为 C、D。不计导线框的电阻，导体棒在两接触点之间部分的电阻为 R，则：

（1）导体棒受到向右的恒力作用从静止开始运动，导体棒的感应电动势和感应电流将如何变化？

（2）导体棒的运动情况将如何变化？

（3）外力做功产生了哪些效果？

（4）如果在导体棒还没有拉出磁场时撤去外力，情况又会怎样？

【答案】

（1）在匀强磁场中，导体棒CD在恒力 F 作用下从静止开始运动，随着速度 v 增大，感应电动势 E = BLv 增大。根据“右手定则”在导体棒内产生由 D→C 的感应电流，感应电流的大小 I = \(\frac{E}{R}\) 也随之增大。当导体棒拉出磁场时感应电动势和感应电流均变为零。

（2）根据“左手定则”，在磁场中的导体棒 CD 受到向左的安培力作用，由于感应电流随导体棒运动速度的增大而增大，安培力 F_A = BIL 也将逐渐增大。根据牛顿第二定律 F – F_A = ma，导体棒将做加速度逐渐减小的加速运动，在拉出磁场前可能做匀速直线运动，也可能速度一直增大；当导体棒拉出磁场后只受恒力 F 作用，将做匀加速直线运动。

（3）外力做功使导体棒 CD 的动能增大，同时感应电流在导体棒中产生了焦耳热。

（4）如果在导体棒 CD 还没有拉出磁场时撤去外力，导体棒受到向左的安培力作用，但速度方向仍然向右的导体棒将做加速度逐渐减小的减速运动，感应电动势和感应电流均减小，所以安培力也减小。导体棒可能在出磁场前已经停止运动，也有可能出磁场时仍然有一定的速度，这种情况下导体棒出磁场后 将做匀速直线运动。

【解析】

命题意图：应用导线切割磁感线产生感应电动势，综合牛顿第二定律、变加速直线运动和焦耳定律定性分析导体棒的运动变化和能量变化。本题要求分类分析不同情况下相关物理量的不同变化趋势，具有较高的科学思维能力要求。

主要素养与水平：运动与相互作用（Ⅲ）；模型建构（Ⅱ）；科学推理（Ⅳ）。

 

67．如图（a）所示，MN、PQ 为间距 L 且足够长的平行导轨，NQ ⊥ MN，导轨的电阻均不计；导轨平面与水平面间的夹角为 θ，NQ 间连接有一个阻值为 R 的电阻；有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为 B₀；将一根质量为 m 的金属棒 ab（长度近似与导轨间距相等）紧靠 NQ 放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至 cd 处时达到稳定速度。已知在此过程中通过金属棒截面的电荷量 q，且金属棒的加速度 a 与速度 v 的关系如图（b）所示，其中 a_m 与 v_m 已知。设金属棒沿导轨向下运动过程中始终与 NQ 平行。求：

（1）金属棒与导轨间的动摩擦因数 μ。

（2）金属棒的电阻 r。

（3）cd 离 NQ 的距离 s。

（4）金属棒滑行至 cd 处的过程中，电阻 R 上产生的热量。

【答案】

（1）由图（b）可知，当 v = 0 时，a = a_m，此时回路中感应电流为零。根据牛顿第二定律，有

mgsinθ − μmgcosθ = ma_m

\[\mu  = \frac{{g\sin \theta  - {a_\rm{m} }}}{{g\cos \theta }}\]

（2）由 图（b）可知：当金属棒速度为 v_m 时，加速度 a = 0。即 当金属棒达到稳定速度 v_m 时，有

F_安 = B₀IL，E = B₀Lv_m，I = \(\frac{E}{{R + r}}\)

mgsinθ = F_安 + μmgcosθ

\[r = \frac{{{v_\rm{m} }B_0^2{L^2}}}{{mg(\sin \theta  - \mu \cos \theta )}} - R = \frac{{{v_\rm{m} }B_0^2{L^2}}}{{m{a_\rm{m} }}} - R\]

（3）q = \({\bar I}\) Δt = \(\frac{E}{{R + r}}\) Δt = \(\frac{{\Delta \Phi }}{{\Delta t}}\)·\(\frac{{\Delta t}}{{R + r}}\) = \(\frac{{{B_0}Ls}}{{R + r}}\)

所以

\[s = \frac{{q(R + r)}}{{{B_0}L}} = \frac{{q{v_{\text{m}}}{B_0}L}}{{m{a_{\text{m}}}}}\]

（4）根据动能定理               mgssinθ – μmgscosθ – W_F = \(\frac{1}{2}\) mv_m² −0

Q_总 = W_F = mgs（sinθ − μcosθ）− \(\frac{1}{2}\)mv_m² = ma_ms − \(\frac{1}{2}\)mv_m² = qv_mB₀L − \(\frac{1}{2}\)mv_m²

电阻 R 上产生的热量为

\[{Q_R} = \frac{R}{{R + r}}{Q_总} = \frac{R}{{R + r}}(q{v_\rm{m} }{B_0}L - \frac{1}{2}mv_\rm{m} ^2)\]

【解析】

命题意图：理解导线切割磁感线产生感应电动势的相关概念和规律，综合应用牛顿第二定律、变加速直线运动、闭合电路欧姆定律和动能定理分析导体棒的运动及其变化，计算相关物理量，具有较高的科学思维能力要求。

主要素养与水平：运动与相互作用（Ⅲ）；模型建构（Ⅱ）；科学推理（Ⅳ）。

 

69．如图所示，有一半径为 r 的导电圆环处于磁感应强度为 B 的匀强磁场中，磁场方向垂直纸面向里且与圆环平面垂直，圆环的电阻为 R，a、b、c 为圆环上等间距的三点。若磁感应强度 B 在时间 Δt 内均匀减小至零，则此过程中圆环内的感应电动势和感应电流分别多大？a、b 间的电压 U_ab 和 b、c 间的电压 U_bc 分别多大？

【答案】

圆环中的感应电动势为 E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) = \(\frac{{B\pi {r^2}}}{{\Delta t}}\)，感应电流为 I = \(\frac{E}{R}\) = \(\frac{{B\pi {r^2}}}{{R\Delta t}}\)

\[{U_{ab}} = {U_{bc}} =  - \left( {\frac{E}{3} - I\frac{R}{3}} \right) =  - \frac{E}{3} + \frac{E}{R}\frac{R}{3} = 0\]

【解析】

命题意图：理解磁感应强度变化产生感应电动势的概念和规律，结合闭合电路欧姆定律分析串联电 源两端的电压，通过计算知道在圆环上任意两点之间的电压均为零。

主要素养与水平：运动与相互作用（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅳ）。

 

69．制造精密电阻时常常采用双线绕法（如图），这种方法有什么优点？

【答案】

变化的电流在线圈中引起自感现象，其感应电流与原电流方向相反，使精密电阻的阻值误差增大。采用双线绕法，两条环绕线绕成的两个线圈的匝数相等，但电流方向相反，两条环绕线产生的磁场大小相等，方向相反，磁场相互抵消，也就防止了线圈的自感现象

【解析】

命题意图：应用自感和“右手螺旋定则”分析实际问题。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

70．如图所示，足够大的匀强磁场垂直于纸面向里，蓝色区域为一处于纸面的金属片。金属片在匀强磁场中垂直于磁感线向右平移，金属片中是否会有涡流？如果将金属片绕 ab 轴旋转，金属片中是否会有涡流？ 试说明理由。

【答案】

金属片在匀强磁场中垂直于磁感线向右平移，金属片内的磁通量没有发生变化，所以金属片中不会产生涡流。如果将金属片绕 ab 轴旋转，金属片内的磁通量发生变化，所以金属片中就有涡流。

【解析】

命题意图：分析具体实例，知道金属内部磁通量的变化是产生涡流现象的根本原因。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

71．在如图所示的电路中，开关 S 先后与位置 1 和位置 2 接通，在这个过程中电路中的能量如何变化？

【答案】

开关 S 与位置 1 接通，电源将部分电能转化为电感器 L 中贮藏的磁场能；然后开关 S 再与位置 2 接通，电感器中贮藏的磁场能部分转化为电阻 R 的焦耳热。

【解析】

命题意图：了解变化的电流通过自感线圈产生自感现象，分析开关闭合和断开两个过程中能量转化的特点。

主要素养与水平：运动与相互作用（Ⅰ）；能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅱ）。

 

72．如图所示电路中，线圈 L 的电阻与另一支路中电阻器 R 的阻值相同。当开关 S 接通瞬间和断开瞬间，两个电流表的示数是否相同？

【答案】

开关 S 接通瞬间，电源向并联电路供电，线圈分支存在自感，所以两个安培计的读数不同，之后两个安培计的读数逐渐趋同；开关断开时两个安培计的读数相同。

【解析】

命题意图：变化的电流通过自感线圈形成自感现象，从具体电路中分析开关 S 接通和断开瞬间形成自感现象时的电流变化特点。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

73．工业上制造白炽灯泡时，为了更好地排出灯泡里的空气，必须对灯泡加热，但有时会把灯泡放在频率较高的交变磁场中，此时灯泡玻璃并不发热，为什么这样做能达到加热的目的？

【答案】

制造灯泡时要抽气封口，但灯泡内金属上吸附的气体，只有在高温下才能迅速释放出来被抽走。所以有时把灯泡放在频率较高的交变磁场中，利用灯泡内金属中产生的涡流来加热金属部分，在加热的同时抽气，然后迅速封口。这种加热方法称为感应加热方法，它们的优点是“热源”不需要和被加热的材料直接接触。灯泡的外层玻璃是绝缘体，当磁场迅速变化时，玻璃中无涡流，故玻璃不发热。

【解析】

命题意图：尝试应用涡流现象解释实际问题。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

74．如图所示，进飞机场、火车站之前，旅客都要过一道安检门，用来检查旅客是否随身携带金属物品，包括枪支、管制刀具等。要是携带了金属物品，安检门就会发出声光警报信号。安检门又称金属探测门，实际上是一种金属探测器，在安检门的两侧装有能发射和接收交变电磁场的仪器。一定频率的交变电流通过线圈产生变化的磁场，该磁场在金属物体内部感生涡电流，接收传感器检取涡电流发射的电磁波信号，再经过电路放大处理，便能以声光形式报警。试列举金属探测器的实际应用。

【答案】

金属探测器可以检测工业原料中的金属异物；在建筑施工中，金属探测器可用于探查地下金属管线的走向和分布；在军事上，金属探测器可用来扫雷；在食品加工过程中检测是否有金属残留物等。

【解析】

命题意图：尝试应用涡流现象解释金属探测器的实际问题。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

75．一矩形线圈在匀强磁场中匀速转动。从经过中性面开始计时，每转一周需时 0.02 s，线圈中产生的感应电动势 e 与时间 t 的关系如图所示的正弦函数。试求：

（1）这一感应电动势的最大值、有效值、周期和频率；

（2）写出这一感应电动势随时间变化的关系式。

【答案】

（1）e_m = 28.28 V，E ≈ 20 V，T = 0.02 s，f = 50 Hz

（2）e = 28.28 sin ( 100πt ) V

【解析】

分析：从感应电动势的图像中可以直接读出电动势的最大值和周期，然后再根据相关公式计算有效值和频率。

根据周期计算频率，结合感应电动势的最大值可以写出感应电动势随时间变化的关系式。

解：（1）从图中可以读出感应电动势的最大值 e_m = 28.28 V，根据有效值与最大值的关系式，可知电动势的有效值

E = \(\frac{{{e_{\rm{m}}}}}{{\sqrt 2 }}\) = \(\frac{{28.28}}{{\sqrt 2 }}\) ≈ 20 V

从图像可知感应电动势变化的周期 T = 0.02 s，频率

f = \(\frac{1}{T}\) = \(\frac{1}{{0.02}}\) Hz = 50 Hz

（2）因为线圈匀速转动，且从经过中性面开始计时，则 t 时刻线圈平面与中性面之间的夹角

θ = ωt = 2πft = 2π×50t = 100πt

所以，这一感应电动势随时间变化的关系式为

e = 28.28 sin ( 100πt ) V

 

76．我国家庭用电一般都是电压为 220 V、频率为 50 Hz 的交变电流，其电压的最大值为多少？每秒内电流方向改变几次？

【答案】

U_m = 220\({\sqrt 2 }\) V ≈ 311 V，每秒钟电流方向改变 100 次。

【解析】

命题意图：理解交变电流最大值和有效值的关系，知道交变电流的频率。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

77．有人说，在下图中，线圈平面转到中性面的瞬间穿过线圈的磁通量最大，因而线圈中的感应电动势最大；线圈平面跟中性面垂直的瞬间穿过线圈的磁通量为零，因而线圈中的感应电动势为零。这种说法是否正确？为什么？

【答案】

不正确。在线圈平面转到中性面的瞬间，如图（a）所示，穿过线圈的磁通量最大，但是 ab 和 cd 边均没有切割磁感线，磁通量的变化率为零，因而线圈中感应电动势为零；在线圈平面跟中性面垂直的瞬间，如图（b）所示，穿过线圈的磁通量为零，但是 ab 和 cd 均垂直切割磁感线，磁通量的变化率最大，因而线圈中的感应电动势最大。

【解析】

命题意图：理解中性面，以及磁通量、磁通量变化率和感应电动势之间的联系和区别。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

78．为什么模型发电机在接通电路前用较小的力就能摇动手柄，接通电路并输出电流后就需要用较大的力才能摇动手柄？

【答案】

摇动手柄使模型发电机的线圈在磁场中旋转，并切割磁感线，接通电路前输出功率为零，提供的机械功率只需要克服线圈转动产生的摩擦阻力。模型发电机接通电路后，提供的机械功率除了要克服线圈转动产生的摩擦阻力以外，还要提供通电线圈和负载的电功率，所以模型发电机在接通电路并输出电流后比接通电路前需要用更大的力摇动手柄。

【解析】

命题意图：应用能量守恒定律解决实际发电机能量转化问题。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

79．如图所示，电解电容器标注“300 V 1.8 μF”，能够接在这个电容器上的交流电电压有效值不能超过多少？

【答案】

电解电容器标注的“300 V”是该电容器能够接交流电的电压最大值，其有效值为 U = \(\frac{{{U_{{\rm{max}}}}}}{{\sqrt 2 }}\) = \(\frac{{300}}{{\sqrt 2 }}\) V ≈ 212.1 V。

【解析】

命题意图：知道电容器标注的电压值是指能够接在电容器两端电压的最大值。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

80．一台交流发电机产生的电压最大值为 150 V，给纯电阻用电器供电时输出的电流最大值为 30 A。试计算：

（1）发电机的电压有效值；

（2）发电机供给外电路的电流有效值；

（3）电路中消耗的功率。

【答案】

（１）U = \(\frac{{{U_{{\rm{max}}}}}}{{\sqrt 2 }}\) = \(\frac{{150}}{{\sqrt 2 }}\) V ≈ 106.1 V

（2）I = \(\frac{{{I_{{\rm{max}}}}}}{{\sqrt 2 }}\) = \(\frac{{30}}{{\sqrt 2 }}\) A ≈ 21.2 A

（3）P = UI = 106.1×21.2 W ≈ 2 249 W ≈ 2 250 W

【解析】

命题意图：理解交变电流最大值、有效值和功率之间的关系。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

81．一只电炉接在电压有效值为 220 V 的交流电源上。求：

（1）电炉使用时，其中的发热元件两端电压的最大值；

（2）如果发热元件的电阻为 11 Ω，通过该元件电流的有效值；

（3） 电炉使用 1 h 消耗的电能。

【答案】

（1）U_max = \({\sqrt 2 }\)U = \({\sqrt 2 }\)×220 V ≈ 311 V

（2）I = \(\frac{U}{I}\) = \(\frac{220}{11}\) A = 20 A

（3）E = UIt = 220×20×3 600 J ≈ 1.58×10⁷ J ≈ 4.4 kW·h

【解析】

命题意图：理解交变电流最大值、有效值和消耗的电能之间的关系。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅱ）。

 

82．一位学生问：“当电流为正时，能量进入灯泡；当电流为负时，能量流出灯泡。因此净流入为零。那么，交变电流为什么还要消耗功率呢？”说明这种说法为什么是错误的。

【答案】

如果灯泡（负载）的两端 A 和 B 接通交流电源。当 电流为正时，如果电流从 A 端流入负载，电流对负载做功，能量流入负载；当电流为负时，电流从 B 端流入负载，电流仍然对负载做功，能量还是流入负载，因此交流电在整个周期内都有能量提供给负载。

【解析】

命题意图：根据交变电流的特点分析用电器的能量转化。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅱ）。

 

83．理想变压器的原线圈匝数 n₁ = 2 200，输入电压为 220 V。为了使副线圈得到 36 V 输出电压，副线圈匝数 n₂ 应为多少？

【答案】

360 匝

【解析】

分析：根据理想变压器的电压比和匝数比的关系，可以求出副线圈匝数。

解：已知 n₁ = 2 200，输入电压 U₁ = 220 V，输出电压 U₂ = 36 V，由

\[\frac{{{U_1}}}{{{U_2}}} = \frac{{{n_1}}}{{{n_2}}}\]

得                                             n₂ = \(\frac{{{U_1}}}{{{U_2}}}\) n₁ = \(\frac{{36}}{{220}}\)×2 200 匝 = 360 匝

所以，副线圈需要 360 匝。

 

84．变压器为什么不能改变恒定电流的电压？

【答案】

恒定电流在变压器的原线圈（初级线圈）内产生的 磁场是恒定的，这个恒定的磁场在副线圈（次级线圈）内不能产生感应电动势，所以变压器的次级线圈也就没有输出电压了。

【解析】

命题意图：理解变压器的原理。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

85．某同学将一个变压器的原线圈接到 6 V 的交变电源上，测得副线圈两端的电压为 2 V。现将原线圈和副线圈对调使用，则输出的电压为多少伏？

【答案】

这个变压器原来是作为降压变压器使用的，将原线圈和副线圈对调以后就成为升压变压器了。原来变压比是 3∶1，现在成为 1∶3 了，所以输出的电压为 18 V。

【解析】

命题意图：理解变压器的原线圈和副线圈是根据实际使用情景命名的，并不是绝对的。

主要素养与水平： 模型建构（Ⅰ）；科学推理（Ⅱ）。

 

86．输送相同的电功率，电压越低，电流越大。常见的向用户送电的变压器是降压变压器，它的原线圈和副线圈哪个电压较低？哪个线圈的匝数较多？哪个线圈的电流较大？为什么？

【答案】

降压变压器的输入电压 U₁ 较高，输出电压 U₂ 较低，由于 \(\frac{{{n_1}}}{{{n_2}}}\) = \(\frac{{{U_1}}}{{{U_2}}}\)，所以降压变压器的初级线圈匝数比次级线圈多。由于副线圈的电压较低，输送相同的功率，副线圈的电流较大。

【解析】

命题意图：理解变压器基本原理及输送功率的概念，分析相关问题推出结论：传输一定的功率，在改变原、副线圈电压的同时也改变通过两线圈的电流。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅰ）；科学论证（Ⅱ）。

 

87．如图所示，四种情况中能够将电压降低向电灯供电的变压器是哪一种？说明判断的理由。

【答案】

能够降低电压向电灯供电是图（b）所示的变压器因为变压器不能改变直流电压，而图（a）和图（c）的输入端接直流电压，输出端电压为零，电灯不亮，因此图（a）和图（c）均错。图（b）初级线圈的匝数多于次级线圈的匝数，是一个降压变压器；图（d）初级线圈的匝数少于次级线圈的匝数，是一个升压变压器。综合以上分析，只有图（b）能够降低电压向电灯正常供电。

【解析】

命题意图：应用变压器的基本原理分析实际问题。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

88．一台笔记本计算机首先从 220 V 的电源通过变压器得到有效值为 9.0 V 的交流电压。如果变压器的初级线圈为 660 匝，次级线圈有几匝？

【答案】

将该变压器视为理想变压器，则次级线圈的匝数为

n₂ = \(\frac{{{U_1}}}{{{U_2}}}\) n₁ = \(\frac{9.0}{220}\)×660 匝 = 27 匝

【解析】

命题意图：应用变压器的基本原理分析计算相关物理量。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

89．某理想变压器原、副线圈的匝数之比为 4∶1。当输入电压为 12 V 时，输出电压为多少？当输入电压减少 2 V 时，输出电压为多少？输入电压的改变量 ΔU₁ 与输出电压改变量 ΔU₂ 之比为多少？

【答案】

参考解答：U₂ = \(\frac{{{n_2}}}{{{n_1}}}\) U₁ = \(\frac{1}{4}\)×12 V = 3 V

U₂ʹ = \(\frac{{{n_2}}}{{{n_1}}}\) U₁ʹ = \(\frac{1}{4}\)×(12 − 2)V = 2.5 V

因为 U₁ = \(\frac{{{n_1}}}{{{n_2}}}\) U₂，所以 \(\frac{{\Delta {U_1}}}{{\Delta {U_2}}}\) = \(\frac{{{n_1}}}{{{n_2}}}\) = \(\frac{4}{1}\)，即输入电压的改变量与输出电压改变量之比为 4∶1。

【解析】

命题意图：应用变压器的基本原理分析并计算电压变化量之比与匝数比之间的关系。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

90．如图所示为输电线路中常用的油浸自冷式变压器。变压器内部的铁芯、线圈浸没于变压器油（一种矿物油，也称导热油）中。变压器工作时，铁芯、线圈会发热。这些热量主要通过导热油流经变压器外部的一根根金属管道散发到空气中，从而使铁芯、线圈的温度不会升高太多，以确保变压器的安全运行。试回答：

（1） 变压器外部的散热器为什么做成管道状？

（2） 变压器的上部有个油箱，其侧面有一个油量表。油量表就是一根上、下两端均开口并插入油箱中的玻璃管。电工通过观察玻璃管中油面的高度来判断油箱中油量的多少。设计这一装置利用的是什么物理规律？

（3） 图示变压器外部的散热管道都是沿竖直方向而不沿水平方向，为什么？

（4） 正常情况下，变压器油箱中的导热油是绝对不允许装得全满的，为什么？

【答案】

（1）变压器工作过程中电流通过原、副线圈产生焦耳热，外部的散热器做成管道状是为了増大对外散热面积，较快降温。

（2）设计这一装置利用的是连通器原理。玻璃管与油箱组成一个充满同样液体的连通器，静止时液面处于同 一高度。

（3）管道沿竖直方向便于变压器中的导热油形成对流增强散热能力。

（4）若变压器油箱中的导热油装得全满，变压器工作过程产生的热量使导热油受热膨胀，容易将变压器胀破造成事故。

【解析】

命题意图：熟悉实际输电变压器外部基本结构和作用。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅰ）。

 

91．能不能用电动机带动发电机，再用发电机输出的电能驱动该电动机而实现发电机和电动机的连续运转？

【答案】

不能实现发电机和电动机的连续运转。电动机和发电机的线圈都存在电阻，在运行过程中，通电线圈产生焦耳热，同时电动机和发电机的轴与轴承之间也存在摩擦阻力，克服摩擦阻力做功也将产生热。根据能量守恒定律，由于存在这些能量损耗，不可能实现发电机和电动机的连续运转。

【解析】

命题意图：了解发电机和电动机的基本原理和能量守恒定律。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅰ）。

 

92．我国自行研制的动车组采用了“再生制动”技术，在车速从 200 km/h 下降到 90 km/h 的过程中可以通过发电机发电，此过程中的能量是如何转化的？为什么要采用这种技术？

【答案】

动车组在减速时不直接采用机械刹车，而是关闭电源，由于动车组具有惯性仍将继续行驶，此时磁场中的线圈随车轮一起转动，使线圈中的部分导线切割磁感线产生感应电动势，这时动车的电动机转变成发电机，把动车组的部分机械能转化为电能。采用此项技术能够节能环保，有利于提高电能利用率，降低动车的运行成本。

【解析】

命题意图：了解电动机的实际应用，进一步理解其能量转化机理及节能设计。有利于形成节能环保观念。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅰ）。

 

93．如图所示是实验室用的手摇交流发电机。把发电机输出端跟小灯泡连接起来，使线圈在磁场中转动，可观察到小灯泡发光。该手摇交流发电机的工作原理是什么？若增加线圈的转动速度，灯泡的亮度如何变化？把两个发光二极管极性相反地并联起来，再与发电机电源输出端串联，缓慢转动线圈，两个发光二极管是否会同时发光？这说明了什么？

【答案】

手摇发电机的工作原理是电磁感应，线圈在磁场中切割磁感线产生感应电动势，线圈与小灯泡组成的闭合 回路产生感应电流使小灯泡发光若增加线圈的转动速度，线圈在磁场中切割磁感线的速度增大，感应电动势增大，使发电机的输出功率增加，小灯泡变亮；两个发光二极管极性相反的并联后再与手摇发电机电源输出端串联，两个发光二极管不会同时发光，而是交替发光，说明手摇发电机输出的是交变电流。

【解析】

命题意图：有利于理解交流发电机的原理和输出交变电流的特点。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）。

 

94．小型电扇接入电路中通电后能转动，其工作原理是什么？在完好的小型电扇的插头处接一小灯泡，用手快速拨动风扇叶片，带动转子转动，发现小灯泡发光，如图所示。简要说明产生这一现象的原因。

【答案】

小型电扇的工作原理是通电线圈在磁体产生的磁场中受安培力作用绕轴转动；用手快速拨动风扇叶片，小型电扇中的线圈在磁场中切割磁感线产生感应电动势，小型电扇的电动机变成了小型发电机。

【解析】

命题意图：有利于理解发电机和电动机的基本原理和能量守恒定律。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）。

 

95．随着科技发展，越来越提倡节能环保。如图所示为一种发电旋转门，该旋转门安装了一个特殊装置，通过人们推动旋转门进出就会产生并存储电能，发电旋转门的工作原理如何？试从能量转换的角度分析。

【答案】

发电旋转门的工作原理是导体切割磁感线在闭合回路中产生感应电流，与发电机工作原理类似；发电旋转门的推门过程中将部分机械能转化为电能。

【解析】

命题意图：了解节能发电装置，有利于形成节能环保观念。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；社会责任（Ⅰ）。

 

96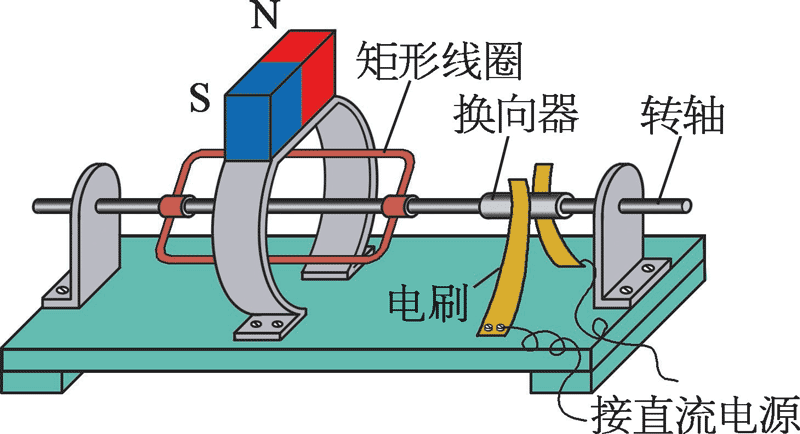．如图所示是某同学自制的“小小电动机”，接通电路后线圈开始转动，如果要使线圈反向转动，可采取哪些方法？

【答案】

改变电流方向或改变磁场方向都会使电动机转动方向与原来相反。

【解析】

命题意图：理解发电机和电动机的基本原理。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅱ）。

 

97．如图所示，放在 U 形磁体中的线圈 A 和线圈 B 用导线串联。当用力使线圈 A 向右运动时，悬挂着的线圈 B 如何摆动？此时的线圈 A 和线圈 B 在原理上类似于什么？

【答案】

若线圈 A 和 B 的绕线方向相同，则线圈 B 向右摆动；反之，线圈 B 向左摆动。此时线圈 A 的运动原理类似于发电机，线圈 B 的运动原理类似于电动机。

【解析】

命题意图：有利于理解发电机和电动机的基本原理和能量守恒定律。

主要素养与水平：运动与相互作用（Ⅰ）；模型建构（Ⅰ）。

 

98．如图所示，在线圈上端放置一盛有冷水的金属杯。接通交流电源，一段时间后，杯内的水沸腾起来。若要缩短上述加热时间，线圈的匝数和交流电源的频率应该如何改变？哪种家用电器的原理与此类似？

【答案】

增加线圈的匝数或者增大交流电源的频率都能缩短加热时间，家用电磁炉的工作原理与此类似。

【解析】

命题意图：有利于知道涡流现象的实际应用。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅰ）；科学论证（Ⅰ）。

 

99．如图所示，矩形线圈 abcd 在匀强磁场中绕 OO′ 轴顺时针（沿 OO′ 方向看）匀速转动时，线圈中产生正弦交流电。从线圈转过图示位置开始计时，设沿 adcba 方向为电流正方向，则线圈中产生的交流电图像是图中的哪一个？说明判断的理由。

【答案】

图示装置的磁感线竖直向上，t = 0 时线圈四条边均不切割磁感线，感应电流为 0；当线圈绕 OOʹ 轴顺时针转 90° 时 ad 边向右切割磁感线，根据“右手定则”判断感应电流的方向是 abcda，此时是负向最大电流；当线圈绕 OOʹ 轴顺时针转 180° 时 ad 边在右边，线圈四条边均不切割磁感线，感应电流为 0；当线圈绕 OOʹ 轴顺时针转 270° 时 ad 边向左切割磁感线，根据“右手定则”判断感应电流的方向是 adcba，此时是正向最大电流；当线圈绕 OOʹ 轴顺时针转 360° 时 ad 边在左边回到原来位置，线圈四条边均不切割磁感线，感应电流为 0。综合上述分析可知图（c）是正确的。

【解析】

命题意图：通过分析线圈转动过程中切割磁感线的情况，进 一步理解交流电的产生原理。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

100．电阻 R₁、R₂ 和交流电源按照如图（a）所示的方式连接，R₁ = 10 Ω，R₂ = 20 Ω。合上开关 S 后，通过电阻 R₂ 的正弦交流电的电流 i 随时间 t 变化的情况如图（b）所示，则通过 R₁ 的电流的有效值为______A，R₂ 两端的电压有效值为______V。

【答案】

I = \(\frac{{{I_{\rm{m}}}}}{{\sqrt 2 }}\) = \(\frac{{0.6\sqrt 2 }}{{\sqrt 2 }}\) A = 0.6 A，U₂ = IR₂ = 0.6×20 V = 12 V

【解析】

命题意图：有利于通过 i – t 图像理解交流电的有效值和最大值之间的关系，用一段电路欧姆定律计算纯电阻两端的电压。

主要素养与水平：科学推理（Ⅱ）；科学论证（Ⅱ）。

 

101．如图所示的电路中，开关 S 断开之前通过灯 L 的电流方向如何？断开之后的瞬间通过灯 L 的电流方向如何？

【答案】

开关 S 断开之前通过灯 L 的电流方向由 a 到 b，断开之后的瞬间通过灯 L 的电流方向由 b 到 a。

【解析】

命题意图：理解变化的电流通过自感线圈形成自感现象，分析前后两个过程的电流变化特点。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

102．如图所示，用理想变压器给电灯 L 供电，如果只增加副线圈匝数，其他条件不变，则变压器输入电压如何变化？变压器输出电压如何变化？电灯亮度如何变化？变压器输入功率如何变化？简述理想变压器传输交变电流过程中的能量转化规律。

【答案】

只增加副线圈匝数，变压器输入电压不变，变压器输出电压变大，电灯变亮，变压器输入功率变大。理想变压器输入的电能经变压器先转化为磁场能，再经变压器将磁场能转化为电能输出。

【解析】

命题意图：应用变压器的基本原理分析相关物理量的变化和能量转化过程。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅱ）。

 

103．如图所示，A、B 是两盏完全相同的白炽灯，L 是电阻不计的电感线圈。如果断开开关S₁，闭合 S₂，A、B 两灯都能同样发光。如果最初 S₁ 是闭合的，S₂ 是断开的，那么，闭合 S₂ 以后，A 灯和 B 灯亮度如何变化？此时如果断开 S₂，A 灯和 B 灯亮度又将如何变化？

【答案】

闭合开关 S₂ 以后，A 灯变亮，B 灯由亮变暗；此时如果断开 S₂ 时，A 灯立即熄灭，B 灯先亮 一下然后熄灭。

【解析】

命题意图：变化的电流通过自感线圈形成自感现象，分析前后两个过程的电流变化特点。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

104．一个匝数比一定的理想变压器在改变输出交流电的电压大小的同时，输出交流电电压的频率是否也改变了？理想变压器输出电压变化的原因是什么？理想变压器输入电功率变化的原因是什么？

【答案】

理想变压器输出交流电压的频率始终等于输入交流电压的频率，所以改变交流电的输出电压不会改变输出的交流电压的频率。匝数比一定的理想变压器所输出电压的变化原因是输入电压的变化。变压器输出端负载变化引起输出电流变化，从而引起输出功率变化。理想变压器输入功率等于输出功率，输出功率变化引起输入电功率也发生变化。由于变压器的输入电压（市电）是固定不变，所以输入电流将随输出功率的变化而变化。

【解析】

命题意图：有利于理解理想变压器原、副线圈之间频率、电压、电流和功率之间的关系。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

105．一电热器接在 10 V 的直流电源上，产生一定大小的热功率。现把它改接到交流电源上，要使它产生的热功率是原来的 2 倍，则交流电压的有效值为多少？交流电压的最大值为多少？（不考虑电阻随温度的变化）

【答案】

R = \(\frac{{U_1^2}}{{{P_1}}}\) = \(\frac{{U_2^2}}{{{P_2}}}\)，U₂ = U₁\(\sqrt {\frac{{{P_2}}}{{{P_1}}}} \) = 10×\(\sqrt {\frac{{2{P_1}}}{{{P_1}}}} \) = 10\({\sqrt 2 }\) V

U_max = \({\sqrt 2 }\)U₂ = \({\sqrt 2 }\)×10\({\sqrt 2 }\) V = 20 V

【解析】

命题意图：进 一步理解交变电流的功率、最大值和有效值的关系。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

106．如图所示，交流电的电压 u = 311sin314t（V），加在一个“220 V 1 000 W”的电饭煲上。试问：

（1） 这个电饭煲能正常工作吗？

（2） 通过这个电饭煲内部电路的电流多大？

（3） 电流瞬时值的表达式是怎样的？

【答案】

（1）交流电压的有效值为 U = \(\frac{{{U_{\max }}}}{{\sqrt 2 }}\) = \(\frac{{311}}{{\sqrt 2 }}\) V ≈ 220 V，与电饭煲额定电压相等，电饭煲能正常工作。

（2）I = \(\frac{{P}}{{U}}\) = \(\frac{{1000}}{{220}}\) A = \(\frac{{50}}{{11}}\) A ≈ 4.55 A

（3）i = \(\frac{{50}}{{11}}\sqrt 2 \) sin314t（A）≈ 6.43sin314t（A）

【解析】

命题意图：从交变电流图像分析最大值和有效值的关系，计算其功率、理解交流电压瞬时表达式中各项的物理意义。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

107．一小型水电站交流发电机的输出功率为 1 000 kW，输出电压为 1 000 V。在输电过程中，要求输电线能量损耗不大于 4%，已知输电线电阻为 16 Ω，用户处的降压变压器输出电压为 240 V。求送电线路中升压变压器与降压变压器各自的变压比。（设升压变压器、降压变压器均为理想变压器）

【答案】

输电线上损失的电功率 ΔP = I₂²R

则电线上的电流为 I₂ =\(\sqrt {\frac{{\Delta P}}{R}} \)  = \(\sqrt {\frac{{1000 \times {{10}^3} \times 0.04}}{{16}}} \) A = 50 A

则升压变压器输出电压为 U₂ = \({\frac{{{P_2}}}{{{I_2}}}}\) = \({\frac{{{P_1}}}{{{I_2}}}}\) = \(\frac{{1000 \times {{10}^3}}}{{50}}\) V = 20×10³ V

输电线量损失的电压 ΔU = I₂R = 50×16 V = 800 V

降压变压器输入电压 U₃ = U₂ − ΔU = （20×10³ − 800）V = 19 200 V

则 n₁∶n₂ = U₁∶U₂ = 1 000∶20×10³ = 1∶20

n₃∶n₄ = U₃∶U₄ = 19 200∶240 = 80∶1

【解析】

命题意图：理解变压器的原理，应用变压器实现远距离输电，知道采用高压输电的原因。

主要素养与水平：能量观念（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅲ）；科学论证（Ⅳ）。

 

108．关于电磁场理论，判断下列说法是否正确，并简述理由。

（1）变化的电场周围产生的磁场一定是变化的。

（2）变化的电场周围产生的磁场不一定是变化的。

（3）任何变化的磁场周围产生的电场一定是均匀变化的。

（4）均匀变化的磁场周围产生的电场才是均匀变化的。

【答案】

（1）错，随时间均匀变化的电场周围产生的是稳定的磁场

（2）正确，随时间均匀变化的电场周围产生的是稳定的磁场

（3）错，变化的磁场产生的电场可以是稳定的也可以是变化的

（4）错，随时间均匀变化的磁场产生的电场是稳定的。

【解析】

命题意图：通过概念辨析，加深对电磁场理论的认识。

主要素养与水平：运动与相互作用观念（Ⅰ）；科学推理（Ⅰ）。

 

109．麦克斯韦根据什么现象提出“变化的磁场能够产生电场”？关于“变化的电场能够产生磁场”的观点是基于什么观念提出的？

【答案】

麦克斯韦根据法拉第电磁感应现象提出了“变化的磁场能够产生电场”的设想。麦克斯韦确信自然界的规律往往是统一的、对称的。

【解析】

命题意图：通过对麦克斯韦电磁理论中对称与统一的认识提升物理观念。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅰ）。

 

110．利用家用电器，动手实验，研究电磁波的发射、接收、反射等现象，并简单交流。

【答案】

以家用遥控器为例，当按动遥控器按钮时，部分遥控器的前方小灯发光，远处的用电器开始工作，这代表电磁波的发射与接收成功，当遮挡遥控器的前方电磁波发射器时，按动遥控器，小灯点亮，但用电器工作状态不变，这说明电磁波的传播受到阻碍；当对着墙壁按动遥控器，小灯点亮，用电器的工作状态也发生了变化，这表明电磁波发生了反射。

【解析】

命题意图：了解生活中电磁波的应用，加强证据意识与交流协作能力。

主要素养与水平：问题（Ⅰ）；证据（Ⅰ）；交流（Ⅰ）；社会责任（Ⅰ）。

 

111．电磁振荡的过程和机械振动过程很相似，试将图所示的过程与弹簧振子的振动相类比。

【答案】

电磁振荡过程与弹簧振子的振动过程的类比

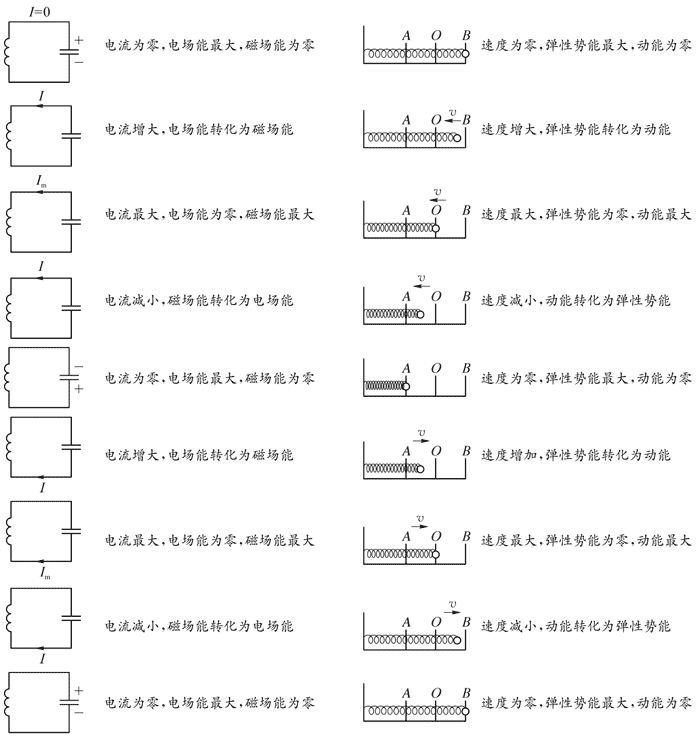
电流为零，电场能最大，磁场能为零              速度为零，弹性势能最大，动能为零

电流增大，电场能转化为磁场能                     速度增大，弹性势能转化为动能

电流最大，电场能为零，磁场能最大              速度最大，弹性势能为零，动能最大

电流减小，磁场能转化为电场能                     速度减小，动能转化为弹性势能

电流为零，电场能最大，磁场能为零              速度为零，弹性势能最大，动能为零

电流增大，电场能转化为磁场能                     速度增加，弹性势能转化为动能

电流最大，电场能为零，磁场能最大              速度最大，弹性势能为零，动能最大

电流减小，磁场能转化为电场能                     速度减小，动能转化为弹性势能

电流为零，电场能最大，磁场能为零              速度为零，弹性势能最大，动能为零

【解析】

命题意图：了解电磁振荡的过程，加强物理规律间的联系。

主要素养与水平：能量观念（Ⅲ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

112．实际的电磁振荡电路中有哪些能量损失？

【答案】

因为线路存在电阻，线路消耗电能；线圈中铁芯内感应电流会产生热量；且交变的电流也能产生电磁波，向空间辐射能量。

【解析】

命题意图：了解电磁振荡中的能量损失，增强理论与实际的联系。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅰ）。

 

113．如何理解电磁场是一种物质？简述理由。

【答案】

电磁波是振荡的电场和磁场在空间传播，由场源向周围传播。不过即使场源消失，电磁波也会继续传播，这体现了电磁场具有完全独立存在的性质，且电磁场具有能量、能与其他物质发生相互作用（事实上电磁场还有质量和动量等一切物质的基本特性），所以电磁场也是一种物质。

【解析】

命题意图：通过学习，感受电磁场的物质特性，增强物理观念。

主要素养与水平：物质观念（Ⅰ）；运动与相互作用观念（Ⅰ）；能量观念（Ⅰ）；科学推理（Ⅰ）；科学论证（Ⅱ）；科学本质（Ⅱ）。

 

114．广播电视、移动通信等通信方式都需要频率资源，占用一定的频率带宽。通常一套电视信号的频带宽度为 8 MHz，若某多媒体广播电视的中心频率为 411 MHz，请计算这一广播电视频率范围对应的波长范围。

【答案】

0.723 ～ 0.737 m

【解析】

分析：根据电磁波的中心频率、频率宽度可得该广播电视的电磁波频率范围。由电磁波频率、波长、波速间的关系，即可求解。

解：由这一电视信号的中心频率 411 MHz、频率宽度 8 MHz 可得，该电视信号的电磁波频率范围是 407 ～ 415 MHz。

当 f₁ = 407 MHz = 4.07×10⁸ Hz 时，对应的电磁波波长

\[{\lambda _1} = \frac{c}{{{f_1}}} = \frac{{3 \times {{10}^8}}}{{4.07 \times {{10}^8}}}\;{\rm{m}} \approx 0.737\;{\rm{m}}\]

当 f₂ = 415 MHz = 4.15×10⁸ Hz 时，对应的电磁波波长

\[{\lambda _2} = \frac{c}{{{f_2}}} = \frac{{3 \times {{10}^8}}}{{4.15 \times {{10}^8}}}\;{\rm{m}} \approx 0.723\;{\rm{m}}\]

因此，该广播电视对应的电磁波波长范围为 0.723 ～ 0.737 m。

 

115．已知地球到月球的距离为 3.84×10⁵ km，如果从地球向月球发射电磁波，经过多长时间才能在地球上接收到反射回来的电磁波？

【答案】

根据 t = \(\frac{s}{c}\)，可知当 s = 2×（3.84×10⁵×10³）m 时，t = 2.56 s。

【解析】

命题意图：了解电磁波传播特性。

主要素养与水平：运动与相互作用观念（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

116．假如赫兹实验发出的电磁波的频率是 1×10⁹ Hz，则这一电磁波的波长为多少？

【答案】

根据 c = λf，可知当 c = 3×10⁸ m/s 时，λ = 0.3 m。

【解析】

命题意图：了解电磁波的波长、频率与波速的关系。

主要素养与水平：科学推理（Ⅱ）；科学本质（Ⅰ）。

 

117．为什么说电磁波是横波？

【答案】

电磁波空间中任意一点的电场 E 的方向和磁场 B 的方向都和电磁波的传播方向垂直。

【解析】

命题意图：了解电 磁波的传播特性。

主要素养与水平：运动与相互作用观念（Ⅱ）；模型建构（Ⅱ）；科学论证（Ⅱ）。

 

118．打开收音机，在收音机旁边放置一个正在工作的手机或者电动剃须刀。调节收音机的方位和距离，看看会发生什么情况，并解释其中的原因。

【答案】

收音机会发出噪声，这代表收音机接收的电台发射的电磁波受到干扰， 也说明电动剃须刀和手机也能够发射电磁波。

【解析】

命题意图：获取电磁波发射与接收的感性素材。

主要素养与水平：运动与相互作用观念（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅰ）；科学论证（Ⅱ）。

 

119．在赫兹验证电磁波存在的实验中，接收器能够在发射器的附近产生电火花说明了电磁波的存在，试从能量的角度解释这一现象。

【答案】

感应发射器通过与高压电源相连，产生电火花形成电磁波，是将电能转化为电磁场的能量，电磁波在空中传播，也传递了能量，接收器将该电磁波能量转化为电能（电火花）。

【解析】

命题意图：通过对物理现象的解释提升物理观念。

主要素养与水平：能量观念（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅰ）；科学论证（Ⅱ）；科学本质（Ⅰ）。

 

120．列举家用电器和生活用品中与红外线、紫外线有关的应用。

【答案】

家用电器中，遥控器通常使用红外线来传递数据，浴霸是利用红外线来加热物体；家庭中使用的假钞检验器利用的是紫外线。

【解析】

命题意图：了解红外线、紫外线在生活中的应用。

主要素养与水平：模型建构（Ⅱ）；社会责任（Ⅱ）。

 

121．近期的科学研究发现，南极和北冰洋上空的臭氧层变薄，甚至出现臭氧空洞。试说明为什么科学家非常关注这种臭氧层变薄的现象？

【答案】

臭氧层破坏后，地面将受到过量的紫外线辐射，危害人类健康。

【解析】

命题意图：通过了解臭氧变薄后效应，提高环保和可持续发展的意识。

主要素养与水平：运动与相互作用观念（Ⅰ）；科学论证（Ⅱ）；科学态度（Ⅱ）。

 

122．太阳辐射的电磁波中，45% 左右的能量在可见光波段，而红外波段能量占比次之，紫外波段则最少。在电磁波谱中，可见光波段的波长范围很小，但是我们人眼却对它最敏感，这是一种巧合吗？查找资料，试解释这一现象。

【答案】

不是巧合，相反的这是生物进化的结果。人们的视觉感知已经进化到了对太阳光的最强波段最为敏感。

【解析】

命题意图：利用物理、生物学知识解释物理现象，经历跨学科融合，提升学科交叉意识。

主要素养与水平：科学论证（Ⅱ）；科学本质（Ⅱ）；科学态度（Ⅱ）。

 

123．简述微波炉与电磁炉加热食物的区别。

【答案】

微波加热的原理是由于食物中含有一定的水分，水分子是极性分子（分子的正负电荷中心不重合），极性分子在微波电场的作用下会剧烈取向振荡，从而使水温升高。食物中含有水分，食物的温度因而也相应升高。

电磁炉是通过电磁感应来加热食物的。通常要采用铁制锅具，当电磁炉内的磁感线穿过铁锅后在铁锅锅底处产生涡流，电能转化为内能，从而通过热传递快速加热食物。

【解析】

命题意图：利用已学知识，对比、解释家电的工作原理，感悟理论与实际的关联。

主要素养与水平：模型建构（Ⅱ）；科学论证（Ⅱ）；社会责任（Ⅱ）。

 

124．在使用微波炉时，很多情况下食物已经热了，但是器皿却不热，试从微波炉的原理出发解释这一现象。有时会发现器皿也比较烫手，为什么会出现这一现象？试从器皿的材质、食物的含水量、微波功率、加热时间等方面考虑进行实验探究。设计一个采用控制变量法的实验方案，在保证安全的前提下开展实验，分析观察，得出结论，并与同学交流。实验前务必仔细阅读微波炉说明书，特别是其中的安全须知。

【答案】

微波加热的原理是由于食物中含有一定的水分子，水分子是极性分子（分子的正负电荷中心不重合），极性分子在微波电场的作用下会剧烈取向振荡，从而使水温升高。加热器皿中则很少含有水分子，因此不会非常热。若发现器皿比较烫手是因为在加热过程中食物与器皿接触，当食物发热后，由于热传递使器皿烫手为了研究器皿的烫手现象是否是因为热传递所引起的，可采用控制变量法，使用对照组，研究微波功率、加热时间、食物含水量、器皿材质（陶瓷、塑料等）等的影响，具体方案略。

【解析】

命题意图：通过利用微波炉加热食品时，容器的热与不热现象的探究，培养科学解释、科学探究的能力。

主要素养与水平：运动与相互作用观念（Ⅰ）；能量观念（Ⅰ）；模型建构（Ⅱ）；质疑创新（Ⅰ）；问题（Ⅱ）；证据（Ⅲ）；解释（Ⅱ）；交流（Ⅱ）；科学态度（Ⅱ）；社会责任（Ⅱ）。

 

125．通常电台信号和电视信号能实现同步转播。现在已知传输无线电广播的信号的频率为 600 kHz，传输电视信号的电磁波频率为 411 MHz，为了让住在山区的人们也能够听到电台广播，看到电视转播，试回答：人们必须在山上建立哪一种信号的基站，简述原因。

【答案】

根据 c = λf 可知，无线广播电视的波长为 500 m，电视信号波长为 0.72 m，根据波的衍射特点，由于电视信号的波长较短，必须采用空间波的传播方式，即点对点的直线传播，因此电视信号要在山上建立基站。

【解析】

命题意图：会使用电磁波的频率、波长和波速间关系进行计算，并能利用衍射规律判断电磁波的传播方式。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅱ）；科学论证（Ⅱ）；社会责任（Ⅱ）。

 

126．从波的形成、波的传播特性等方面，列举电磁波与声波的三个相似处或不同处，并作简单说明。

【答案】

声波是机械波。从产生机理看，机械波的形成需要机械振动，电磁波则可通过电磁振荡产生。从传播特性上看，机械波传播需要介质，而电磁波的传播不需要介质。电磁波和机械波均有波长、频率、波速的概念，并均满足关系 v = λf，其中电磁波的传播速度可用 c 表示。本题还可从传播能量、信息等方面阐述。

【解析】

命题意图：通过比较，了解机械波及电磁波间的异同，建立概念和规律间的内在联系，提升物理观念。

主要素养与水平：物质观念（Ⅰ）；运动与相互作用观念（Ⅰ）；能量观念（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）；科学本质（Ⅰ）。

 

127．对讲机是一种双向移动通信工具，因为其在无网络支持的情况下也可以通信，所以即使是在手机通信如此发达的今天也仍然被广泛使用。若某同学使用对讲机与 5 km 以外的人联系，对讲机发出的电磁波频率为 470 MHz，则该电磁波的波长为多少？使用对讲机接收信息的人至少需要多久才能接收到电磁波信号？

【答案】

根据 c = λf 可知，电磁波的波长为 0.64 m；又根据电磁波在空气中的传播速度约 3×10⁸ m/s 及 t = \(\frac{s}{c}\) 可知，t = 1.66×10⁻⁵ s。

【解析】

命题意图：学会使用电磁波的频率、波长和波速间关系进行计算，并知道对讲机使用的电磁波波长，鼓励学生留意身边的事物，加强理论与实际的关联。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅱ）；社会责任（Ⅰ）。

 

128．北极星是一颗恒星，距离地球 1.06×10¹³ km，则北极星与地球的距离为多少光年？如果从某天开始，北极星的燃料耗尽不再发光，那么多久之后人们就再也看不见它了？

【答案】

光在真空中传播一年的长度称为光年，用 ly 表示，1 ly = 3×10⁸×365×86 400 m ≈ 9.46×10¹⁵ m，因此北极星离我们的距离 l = 1.06×10¹³ km ≈ 1.12 ly。根据电磁波在真空中（宇宙）中的传播速度 3×10⁸ m/s 可知，北极星的光线照射到地球上需要传播的时间为 3.5×10⁷ s ≈ 405 天。

【解析】

命题意图：知道光是一种电磁波，满足电磁波的频率、波长和波速间关系，能将电磁波的基本知识与天体中的概念相关联。

主要素养与水平：运动与相互作用观念（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）；科学本质（Ⅰ）。

 

129．某氦氖激光器发出的红光波长范围非常窄，中心波长为 632.80 nm，宽度为 0.01 nm。求该激光器发射的红光中心频率及频率范围。

【答案】

根据 c = λf 可知，氦氖激光器的红光中心频率为 4.7×10¹⁴ Hz，根据氦氖激光器的波长范围得到激光器的频率范围为 7.5×10⁹ Hz。

【解析】

命题意图：掌握电磁波的频率、波长和波速间关系，了解激光器的中心频率和特征。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅱ）；社会责任（Ⅰ）。

 

130．若某种电磁波在真空中的频率为 600 MHz，试回答下列问题：

（1）该电磁波的波长为多少？

（2）该电磁波属于哪一波段？

（3）若该电磁波从真空射入水中，判断电磁波的频率、传播速度及波长分别如何变化。

【答案】

根据 c = λf 可知，电磁波的波长为 0.5 m，属于无线电波的分米波波段。电磁波频率 f 不变，传播速度变小，波长变短。

【解析】

命题意图：掌握电磁波的频率、波长和波速间关系，会通过波长或频率查找无线电波的波段，了解电磁波的传播特点。

主要素养与水平：运动与相互作用观念（Ⅰ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

131．查找资料，了解在哪些环境中不适合使用手机，简述原因。

【答案】

电磁波携带能量，长期大量的电磁波辐照能使人体器官遭受损害；且电磁波间的相互干扰会影响仪器的正常使用，并对人们的生产、生活产生危害，如在飞机起飞、降落过程中使用手机会干扰仪器，严重的会造成失控。

【解析】

命题意图：通过查找资料，了解电磁波的安全使用要求，感悟物理态度与责任。

主要素养与水平：社会责任（Ⅱ）。

 

132．为了加强电磁环境管理，保障公众健康，我国制定了相当严格的电磁辐射标准，标准规定通信频段每平方厘米电磁辐射功率应控制在 40 μW 及以下，远低于一些发达国家标准。若某小型通信发射基站的功率为 1 W，同时假设能量以球面向外辐射，请计算：按照标准规定，距离该基站多远处为安全区域？（球表面积为 S = 4πR²）

【答案】

由于电磁波能量是以球面波形式由基站向外辐射，半径为 R 的球面上每平方米的电磁辐射能量为 \(\frac{1}{{4\pi {R^2}}}\)，若按照题目要求不得超过 0.4 W/m²，则通过计算可知，R = 0.45 m。

【解析】

命题意图：能用物理概念及规律解释现象，通过电磁辐射的模型构建和计算解决问题，感悟环境安全、公众健康对可持续发展的意义。

主要素养与水平：能量观念（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅱ）；社会责任（Ⅱ）。

 

133．列举一些在生活与学习环境中接触过的敏感元件，并说明各自感知的物理量。

【答案】

热敏元件感知温度、光敏元件感知光线、气敏元件感知气体、力敏元件感知作用力、磁敏元件感知磁场、湿敏元件感知湿度、声敏元件感知声音、放射线敏感元件感知放射线等。

【解析】

命题意图：引导学生关注生活中应用的各种敏感元件及其工作原理。

主要素养与水平：模型建构（Ⅰ）。

 

134．热敏电阻和金属热电阻都可以作为感知温度的敏感元件。简述两者电阻随温度变化的特点。

【答案】

金属热电阻的阻值随温度的升高而增大。热敏电阻的阻值随温度升高，其阻值的变化情况与材料有关，有的热敏电阻的阻值随温度的升高而增大，有的是随温度的升高而减小，还有一种“开关型”的热敏电阻，其阻值先是随温度升高而增大；当达到某一温度时，电阻突然减小；当温度继续升高到某一温度时，电阻值又随温度升高而增大。

【解析】

命题意图：厘清金属热电阻与热敏电阻的材料差异及其导电特性的差异，关注半导体材料的研究。也是引导学生关注“大家谈”对学习的帮助。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅱ）。

 

135．在地震、海啸等自然灾难发生后，救援人员必须及时深入灾区，争分夺秒抢救被埋人员。有些救援队借助生命探测仪发现深埋在废墟中的伤员。生命探测仪可能应用了哪种传感器？举例并说明理由。

【答案】

可能是红外线传感器。任何物体只要温度在绝对零度以上都会产生红外辐射，人体也是天然的红外辐射源。红外生命探测仪探测出遇难者身体的热量，帮助救援人员确定遇难者的位置。

也可能是声音传感器。如果幸存者已经不能说话，只要用手指轻轻敲击发出微小的声响，就能被声音传感器感知。此外，声音传感器还能检测出心脏的跳动，从而找到伤员也可能同时装有以上两种传感器。

【解析】

命题意图：引导学生认识技术不仅为人类服务，让社会进步，还能在关键的时候拯救生命，潜移默化地进行生命教育，领会学习的责任。

主要素养与水平：科学推理（Ⅱ）；社会责任（Ⅱ）。

 

136．哪些家用电器中没有传感器？哪些家用电器中有传感器？分别有哪些传感器？试举例说明。

【答案】

如电吹风、照明灯、电烙铁、指针式多用表等无传感器。

如电视机遥控器有的是用红外传感器，也有的是用声控传感器。电冰箱、电饭煲的温控采用温度传感器。家用饮水器里有温度传感器、压力传感器等。

【解析】

命题意图：让学生感受到现在已很少没有传感器的家用电器了，说明传感器在现代家用电器中已广泛应用。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅰ）。

 

137．为解决楼道的照明，常在楼道内安装一个声控传感器与电灯的控制电路相连接。当楼道内有人走动而发出声响时，电灯即与电源接通而发光，输入传感器的是什么信号？经传感器转换后输出的是什么信号？

【答案】

行人发出的声响，作为声音信号，被声控传感器接收而转为电信号。

【解析】

命题意图：明确传感器的基本功能是通过将非电学量转换成电学量实现自动控制的。进一步领会非电学量转换为电学量的意义。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅱ）。

 

138．某种热敏电阻的阻值 R 随温度 t 变化的图像如图所示。现将该热敏电阻和电源、电流表串联做成一个电子温度计。为了便于读数，把电流表上的电流值转换成温度值。为使该温度计的变化反应较为灵敏，试判断该温度计测量哪一段范围内的温度较为适宜，并说明理由。

【答案】

应测量 t₂ ~t₃ 范围内的温度。因为此范围对应的图像的斜率较大，即相同的温度改变导致电阻改变得更大，使电流的改变也更大，温度计表现得更灵敏。

【解析】

命题意图：从图像中获取信息，理解灵敏度的意义。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅱ）。

 

139．磁传感器利用霍尔元件测量磁感应强度。如图所示为霍尔元件的测量原理示意图。将一块长方形的半导体薄片放在匀强磁场中，a、b 和 M、N 为相互两两正对的四个电极，在 a、b 间通入恒定的电流，则薄片中可自由移动的电荷受到洛伦兹力的作用，将在两侧形成堆积，使 M、N 间产生电压 U_MN。磁场越强，电荷堆积越多。则：

（1）若移动电荷为负电荷，此半导体的 M 面的电势高还是 N 面的电势高？

（2）若通电电流和磁场都不变，仅将电极 N 沿 ab 方向平移至N′，则电压 U_MN 的数值是否也会发生变化？判断并说明理由。

【答案】

（1）根据左手定则，只要电流方向不变，无论移动的电荷是正电荷还是负电荷，安培力的方向都是指向 N 侧的，即负电荷偏向 N 侧面，N 面上聚集的是负电荷，因此 M 的电势比 N 要高。

（2）若将电极 N 沿 ab 方向平移至 N′，由于材料是有电阻的，沿电流方向电势会降低，即电势 U_N′ < U_N。当移动的是负电荷，因此 M、N 之间的电势差将会变大。当移动的是正电荷，N 的电势比 M 要高，则 M、N 之间的电势差将会变小。若 NN′ 之间的距离足够大，则 M、N 之间的电势差先变小、直到减为零后再反向变大。

【解析】

命题意图：了解磁传感器中的核心元件（霍尔元件）的基本原理是基于洛伦兹力的作用，进一步巩固带电粒子与电场、磁场的相互作用。

主要素养与水平：运动与相互作用（Ⅱ）；科学推理（Ⅱ）。

 

140．火灾探测器是火灾自动报警系统的触发装置，在发生火情初期通常会出现哪些可被感知的物理量？通过哪些传感器能变成电信号，传输到火灾报警系统，从而起到对火灾预警与监控作用？

【答案】

燃烧所产生烟雾的密度、温度（升高）和光辐射等是可被感知到的物理量。通过温度传感器、烟雾传感器和光传感器可将在火灾初期的火灾信号转变成电信号。

【解析】

命题意图：引导学生寻找生活中的物理量与所学传感器知识的联系，重视火灾的防范。

主要素养与水平：模型建构（Ⅰ）；社会责任（Ⅰ）。

 

141．为了省电，常见的楼道灯都由两个开关一起控制。一个是利用光敏电阻制成的“光控开关”，它在光线暗时自动闭合、光线亮时自动断开；一个是利用声敏元件制成的“声控开关”，它在有声音时自动闭合，一段时间无声音则自动断开。试将如图所示的器材连接成符合省电要求的电路。

【答案】

如图所示电路要求光控开关和声控开关同时控制一盏灯，当自然光暗到一定程度，且环境有一定的声音时电灯才点亮，两个开关和灯泡应该是串联的。

【解析】

命题意图：引导学生思考生活场景的应用与节约用电的问题。电路中的开关控制用电器时，通常是只用一个开关和用电器串联，当光暗到一定程度或有声音时都能使电灯点亮，但这样做不满足节约用电的要求。若是光线暗而无行人通过，或者是有行人通过而光线充足，就都不需要开启路灯。本题是打破常规，利用一个简单的问题，启发学生敢想敢做的创新意识。

主要素养与水平：科学推理（Ⅱ）；社会责任（Ⅱ）。

 

142．如图（a）所示是某生产流水线上的产品输送及计数装置示意图。S 为激光源，R₁ 为光敏电阻（有光照时阻值减小），R₂ 为定值电阻，a、b 之间接示波器。水平传送带匀速前进，产品通过时会挡住激光源发出的光线。示波器显示的电压随时间变化图像如图（b）所示。若计数器电路中的电源电压恒为 6 V，电源内阻忽略不计，定值电阻 R₂ = 1 kΩ，求：

（1）无光照时光敏电阻 R₁ 的阻值。

（2）有光照时光敏电阻 R₁ 的阻值。

（3）每小时通过的产品个数。

 

                 (a) 计数装置示意图                            (b) 电压随时间变化图线

【答案】

（1）无光照时，光敏电阻的阻值大、分压大，由图（b）可知无光照时示波器所示的 R₁ 上所分得的电压为 4 V，由 \(\frac{{{U_1}}}{{{R_1}}}\) = \(\frac{{{U_2}}}{{{R_2}}}\) 得 R₁ = \(\frac{{{R_2} \times 4{\rm{V}}}}{{6{\rm{V}} - 4{\rm{V}}}}\) = 2 000 Ω。

（2）有光照时，光敏电阻阻值小、分压小，由图（b）可知有光照时 R₁ 上所分得的电压为 2 V，此时 R₁′ = \(\frac{{{R_2} \times 2{\rm{V}}}}{{6{\rm{V}} - 2{\rm{V}}}}\) = 500 Ω。

（3）由图（b）可知一个周期 T = 0.6 s，所以每小时通过的产品个数为 n = \(\frac{{3600}}{{0.6}}\) = 6 000 个。

【解析】

命题意图：通过电路计算复习串联电路知识，但重点是要学生读懂传感器与电路连接的关系，能从图像中获取传输周期与每一件产品通过时间的关系。体会 STSE。

主要素养与水平：模型建构（Ⅱ）；科学推理（Ⅱ）。

 

143．传感器在日常生活中的应用越来越广泛，利用温度传感器制成的温控开关就是其中的一种。烘箱就是利用温控开关来自动控制电路的。常温下，该开关是闭合的；当温度达到某一设定值时，开关自动断开，从而切断整个电路。如图所示的四个电路图中，能够实现自动控温的是哪一种？判断并说明理由。

【答案】

图中的（a）电路。（b）（c）（d）三种电路中，温度传感器与烘箱并联，当一条支路中的传感器断开时，另一条支路中的烘箱仍在工作，这样就不能达到自动控制电路的作用。

【解析】

命题意图：让学生思考和分析家用电器中的自动化实现的一些思路方法，感受学以致用。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

144．有些楼道的照明灯是声音控制的，当人过来发出声响就会发光，人离开后就会熄灭。这种照明灯内部至少包含了哪两种传感器？

【答案】

声音传感器，光传感器。

夜晚时灯是声音控制的，说明有声音传感器。白天楼道光照充足，即使有人路过发出声响，楼道照明灯也不应点亮，只有夜晚光线不足时，才可能点亮，说明要有光传感器。

【解析】

命题意图：启发学生创设情景，通过科学推理得出结论。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅰ）。

 

145．在生活中使用传感器已很普遍，试问：

（1）电梯超载时会自动报警。这种报警系统通常采用的是什么传感器？

（2）光电式感烟探测器［简称烟感器， 图（a）］由光源、光电元件和电子开关组成。利用光散射原理探测火灾初期产生的烟雾，并及时发出报警信号。烟感器利用的是什么传感器？

（3）在很多洗手间中都装有自动干手机［图（b）］，洗手后将手靠近，自动干手机内的传感器就开通电热器加热，有热空气从内部吹出，将湿的手烘干。自动干手机通常采用的是什么传感器？

【答案】

（1）力传感器（2）光传感器（3）红外传感器

电梯超载是指超过电梯设计的安全载重量，所以超载报警用的是力传感器。烟雾的产生使仪器周围的光强发生改变，所以是光传感器。人手具有一定的温度，发出的红外线可被红外传感器接收而工作，所以是红外传感器。

【解析】

命题意图：旨在引导学生关注日常生活环境中所用的各种电气或设备中传感器的基本物理原理，体会物理就在我们身边。

主要素养与水平：科学推理（Ⅰ）。

 

146．关于敏感元件的特性，判断下列说法是否正确，并说明理由。

（1）热敏电阻是把温度转化为电阻的敏感元件。

（2）金属热电阻是阻值随温度升高而减小的敏感元件。

（3）电熨斗中的双金属片是力敏感元件。

（4）霍尔元件是能够把磁感应强度转换为电压的敏感元件。

【答案】

（1）表述错误。热敏电阻是把温度这个热学量的变化转换为电阻这个电学量的变化。

（2）表述错误。金属热电阻的阻值随温度的升高而增大。

（3）表述错误。电熨斗中的双金属片是温度传感器。

（4）表述正确。霍尔元件中的电荷受磁场力的作用在薄片两侧积累，产生电压，通过这个电压来确定磁感应强度的大小。

【解析】

命题意图：旨在引导学生进一步熟悉和巩固几种常见传感器工作时是将哪些非电学量转换为电学量。

主要素养与水平：科学推理（Ⅰ）。

 

147．将热敏电阻 R_T、定值电阻 R、电流表、电源按图 9–30 连接成电路。将烧杯装入 \(\frac{2}{3}\) 的水，并用铁架台固定在加热器上。闭合开关 S，当热敏电阻未放入热水中时，电流表的示数为 I₁；将热敏电阻放入温水中，电流表的示数为 I₂；将热敏电阻放入热水中，电流表的示数为 I₃。试判断 I₁、I₂、I₃ 的大小关系。

【答案】

若是正温度系数热敏电阻，则其电阻值随温度的升高而增大，故 I₁ > I₂ > I₃。若是负温度系数热敏电阻，则其电阻值随温度的升高而减小，故 I₁ < I₂ < I₃。

【解析】

命题意图：旨在使学生明确认识到，不同材料的热敏电阻，其阻值变化的特点也不同。

主要素养与水平：科学推理（Ⅰ）。

 

148．自 2019 年起，上海新投运的公交车全部采用新能源，近千辆新能源公交车的充电管理都通过云平台自动监控。原先充电主要靠手动和目测，若插歪充电枪，很容易导致枪头温度过高而损害设备甚至引发火灾。为保证安全，试设计一个自动监控新能源公交车充电过程的简要方案。

【答案】

可以在充电枪头上安装一个温度传感器，实时监控温度的变化，超过规定的温度就向管理人员发出信息或警告。

【解析】

命题意图：通过具体实例的分析和设计，增强学生利用所学知识解决实际问题的能力。

主要素养与水平：科学推理（Ⅰ）；社会责任（Ⅰ）。

 

149．在某创新竞赛中，一位学生设计了一个利用压力传感器、光控开关等元件的机动车超载自动拍照电路。一有车辆通过路口且此车超重，摄像机便会自动拍摄。简述他的设计思路。

【答案】

将光控开关和压力开关串联。当有车辆通过时，光控开关会自动闭合；若车辆超重，压力开关会闭合；当两者都闭合时，摄像机才会被激活进行自动拍摄。

【解析】

命题意图：通过具体实例问题的分析和设计，增强学生利用所学知识解决实际问题的能力。

主要素养与水平：科学推理（Ⅱ）；科学态度（Ⅰ）。

 

150．如图所示，R_T 为负温度系数热敏电阻（阻值随温度升高而减小），R₁ 为光敏电阻，R₂ 和 R₃ 均为定值电阻，电源电压保持不变，V 为理想电压表。若发现电压表的示数增大，可能是由于温度或者光照情况发生了变化，试判断具体发生了怎样的变化。

【答案】

热敏电阻的温度升高，或者是光照减弱。

【解析】

命题意图：运用闭合电路中电压表的变化判断相关电阻的变化，本题用热敏电阻或光敏电阻替代以往的滑动变阻器，实现自动化调节。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

151．如图（a）所示是一种酒精测试仪，酒精测试仪实际上是由酒精气敏传感器（相当于随酒精气体浓度变化的变阻器）与一个定值电阻及一个电压表组成。如图（b）所示是这种酒精测试仪的原理图，图中 R₀ 为定值电阻，酒精气敏传感元件 R₁ 的电阻值随酒精气体浓度的增大而减小。简要说明这种酒精测试仪的工作原理。

【答案】

在对酗酒者进行测试时，酒精气体使 R₁ 的阻值减小，导致电路中的电流变大，由欧姆定律可知电压表的示数变大，因此我们就可以通过电压表的示数大小判断此人是否喝了酒。

【解析】

命题意图：用电压表的示数变化测试呼出气体中的酒精浓度，既感受将知识转化为技术的价值和意义，也进行潜在的安全教育与生命教育。

主要素养与水平：科学推理（Ⅱ）；社会责任（Ⅰ）。

 

152．全自动洗衣机中采用了很多传感器。如图所示是安装在排水管两侧的浊度传感器，它用于检测洗净程度。洗涤前，排水管中充满清水，光敏电阻的阻值较小。当洗涤开始后，衣物上的污垢不断地扩散到水中。简述全自动洗衣机利用“光控”从开始洗涤到判断何时结束洗涤的设计思路。

【答案】

洗涤过程中水逐渐变浑浊，致使透光率降低，光敏电阻的阻值变大，继续保持洗涤。一段时间后，当洗涤水变清光敏电阻的阻值减小到一定数值时，给出电信号结束洗涤。

【解析】

命题意图：运用所学传感器知识分析日常生活中自动控制设备的工作原理，感受将知识转化为技术的价值和意义。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

153．无人驾驶飞机的飞行控制系统简称“飞控”。无人机悬停还是飞行、上升还是下降等飞行指令都由“飞控”下达，以保持无人驾驶飞机的正常飞行姿态。无人驾驶飞机内通常有陀螺仪、加速度传感器、地磁感应器、气压传感器、超声波传感器、光流传感器、位置传感器等传感器。为实现飞行姿态自动感知、悬停高度控制、低空高度精确控制或避障、水平位置高度定位、悬停水平位置精确确定等功能，分别需要使用哪种传感器？

【答案】

陀螺仪—飞行姿态感知，气压传感器—悬停高度粗略控制，超声波传感器—低空高度精确控制或避障，光流传感器—悬停水平位置精确确定，GPS 模块—水平位置高度粗略定位。

【解析】

命题意图：现代无人机应用很广泛，引导学生关注生活中的新景象与所学知识的联系。传感器技术是自动化技术的重要标志，旨在吸引对传感器有兴趣的同学敢于联想和尝试，培养创新意识。（光流传感器利用的是图像的变化处理，用于检测地面的状态，从而监测飞机的移动；主要用于保持飞机的水平位置，以及在室内实现定高和定点飞行）

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。