1．将物理课本从放在地上的书包中取出并放到课桌上的过程中，需克服重力做功约________J。

【答案】

4（答案在合理范围即可）

 

2．用一水平拉力拉着质量为 50 kg 的物体沿水平路面匀速运动了 20 m。若物体受到的阻力为 100 N，则此过程中重力对物体做功_________J，地面支持力对物体做功________J，阻力对物体做功_________J，水平拉力对物体做功________J。

【答案】

0，0，− 2 000，2 000

 

3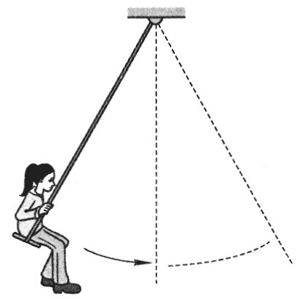．如图所示，若将秋千坐板和人作为一个整体，分析其由最高点摆动至最低点的受力和做功情况，完成下表。

作用力	是否做功	正功还是负功

【答案】

见下表（要求学生至少填出两个，“空气阻力”为选择性要求，判断合理均为正确）

作用力	是否做功	正功还是负功
重力	是	正功
绳的拉力	否
空气阻力	是	负功

 

4．下列关于功的说法中，正确的是（    ）。

A．功的正负表示方向

B．用 100 N 的恒力推箱子做的功总是大于用 10 N 的恒力推箱子做的功

C．在力的作用下物体发生了位移，则该力一定对物体做了功

D．力对物体做了负功，也可以说物体克服该力做了功

【答案】

D

 

5．如图所示，质量为 m 的小物体（可视为质点）从倾角为 θ、高为 h、动摩擦因数为 μ 的固定斜面顶端滑到斜面底端的过程中，重力对物体做功 W_G = ___________；斜面和物体间的摩擦力对物体做功 W_f = _________；斜面对物体的支持力做功 W_N  = _________。

【答案】

mgh，− μmghcotθ，0

 

6．物体在水平恒力 F 的作用下，先在光滑水平面上由静止开始前进，位移为 s，再进入粗糙水平面继续前进，位移也为 s。设恒力 F 在第一段位移 s 中对物体做功为 W₁，在第二段位移 s 中对物体做功为 W₂，则（    ）。

A．W₁ > W₂

B．W₁ = W₂

C．W₁ < W₂

D．无法判断

【答案】

B

 

7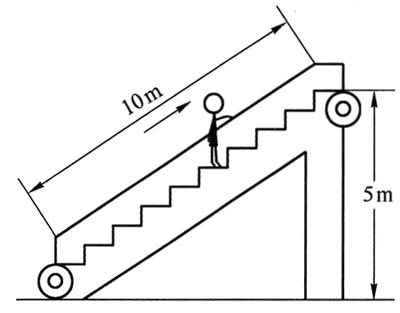．如图所示，长为 10 m 的自动扶梯把质量为 60 kg 的顾客送到 5 m 高的楼上。重力加速度 g = 10 m/s²，若此过程中顾客的运动近似为匀速运动。

（1）顾客所受的重力做了多少功？

（2）自动扶梯的支持力对顾客做了多少功？

【答案】

（1）W_G = − 3 000 J

（2）W_N = 3 000 J

【解析】

（1）重力做功 W_G = −mgh = − 60×10×5 J = − 3 000 J

（2）顾客做匀速运动，由平衡条件知支持力 F_N 竖直向上、大小等于 G，故支持力做功 W_N = F_Nh = mgh = 60×10×5 J = 3 000 J。此小题也可通过动能定理求解如下：顾客做匀速运动，动能不变，由动能定理知其所受支持力 F_N 与重力 G 做功之和等于零，即 W_N = − W_G = 3 000 J。

 

8．如图所示，光滑水平地面上有一个质量 m =  25 kg 的木箱，在大小为 200 N、与水平方向成 37° 斜向上的恒定拉力 F 的作用下，向右前进了 30 m。重力加速度 g = 10 m/s²。该过程中，重力 G、弹力 N 和拉力 F 分别对木箱做的功为多少？

【答案】

零，4 800 J

【解析】

由题意，弹力 F_N 和重力 G 沿竖直方向，位移 s 水平向右，由恒力做功公式 W = Fscosα，而 cos90° = 0 易知，弹力 F_N 和重力 G 与位移方向垂直，故做功为零。

拉力 F 对木箱做的功 W_F = Fscosθ = 200×30×cos37° J = 4 800 J

 

9．光滑水平面上某质量 m = 5 kg 的物体受到水平向北的恒力 F₁ = 8 N、水平向东的恒力 F₂ = 6 N 作用（俯视图如图所示）。求物体由静止开始运动 10 s 的过程中，

（1）F₁ 对物体所做的功 W₁；

（2）F₂ 对物体所做的功 W₂；

（3）合力对物体所做的功 W。

【答案】

（1）W₁ = 640 J

（2）W₂ = 360 J

（3）W = 1 000 J

【解析】

由力的合成可知，物体所受合力 F =10 N、沿北偏东37°方向，由牛顿第二定律知，物体具有沿合力方向的加速度 a = \(\frac{F}{m}\) = \(\frac{{10}}{5}\) m/s² = 2 m/s²。

由静止开始在 10 s 内，物体沿合力方向匀加速直线运动位移 s = \(\frac{{1}}{2}\)at² = \(\frac{{1}}{2}\)×2×10² m = 100 m。

又 F₁ 与位移的夹角 α = 37°，F₂ 与位移的夹角 β = 53°，由恒力做功公式 Fscosθ 知，

（1）W₁ = F₁scosα = 8×100×cos37° J = 640 J

（2）W₂ = F₂scosβ = 6×100×cos53° J = 360 J

（3）合力做功 W = W₁ + W₂ =（640 + 360） J = 1 000 J。此小题也可通过合力做功来求解：W = Fs = 10×100 J = 1000 J

 

10．质量为 m = 2 kg 的花盆自 h = 5 m 的窗台掉落，重力加速度 g = 10 m/s²。花盆下落阶段重力的平均功率为__________W；即将接触地面时重力的瞬时功率为_______W。

【答案】

100，200

 

11．质量为 60 kg 的人站在电梯内，随电梯从静止开始以 2 m/s² 的加速度竖直向上运动 4 m 的过程中，电梯对人做的功为_________J，平均功率为_______W。（g 取10 m/s²）

【答案】

2 880，1 440

 

12．功率为 10 W 的发光二极管（LED灯）的亮度与功率为 60 W 的白炽灯相当。为了提高能效，保护环境，普通照明白炽灯应被逐步淘汰。假设每户家庭原有 2 只 60 W 的白炽灯，均用 10 W 的 LED 灯替代，估算全国一年节省的电能约________kW·h。（假设全国约 4.3 亿户家庭，每户每天亮灯 4 h）

【答案】

6.28×10¹⁰

【解析】

全国一年节省的电能最接近 W = Pt =2×（0.06 − 0.01）×4.3×10⁸×4×365 kW·h ≈ 6.28×10¹⁰ kW·h。

 

13．列车从静止开始匀加速运动，经过 500 m 的路程后，速度达到 360 km/h。整个列车的质量为 1×10⁵ kg，如果不计阻力，在匀加速阶段牵引力的最大功率是_______W。

【答案】

1.00×10⁸

 

14．在光滑的水平面上，用一水平方向的恒力 F 使质量为 m 的物体从静止开始沿直线运动。经时间 t，恒力 F 的瞬时功率为_________。

【答案】

\(\frac{{{F^2}t}}{m}\)

 

15．某日电梯坏了，小欣只好从一楼走楼梯去十九楼。设小欣质量为 50 kg，走到十楼用了 2 min，休息 30 s 后，又花了 2 min 走到十九楼。如果每层楼高 3.0 m，则全过程中小欣克服重力做功的平均功率为________W。（g 取10 m/s²）

【答案】

100

 

16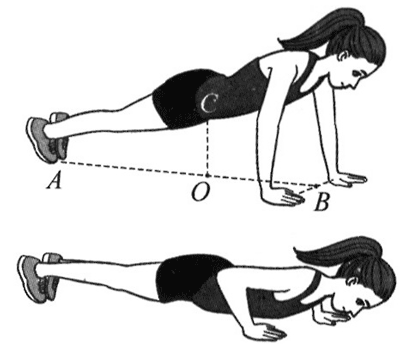．如图所示，质量为 60 kg 的某运动员在做俯卧撑运动。运动过程中可将她的身体视为一根直棒，已知重心在 C 点，C 在地面上的投影 O 与两脚、两手连线中点间的距离 OA、OB 分别为 0.9 m 和 0.6 m。若已知运动员在 1 min 内做了 30 个俯卧撑，每次肩部上升的距离均为 0.4 m，g 取10 m/s²，则她克服重力做功的平均功率为_______W。

【答案】

72

【解析】

此处计算 1 min 内克服重力做功的平均功率，时间用总时间代入计算，不要求算出上升过程时间

 

17．将几节自带动力的车厢（动车）加几节不带动力的车厢（也叫拖车）编成一组就是动车组。假设动车组运行过程中受到的阻力与其重力成正比，每节动车与拖车的质量都相等，每节动车的额定功率都相等。若 1 节动车加 3 节拖车编成的动车组最大速度为 120 km/h，则 6 节动车加 3 节拖车编成的动车组的最大速度为（    ）。

A．300 km/h                              B．320 km/h

C．340 km/h                              D．360 km/h

【答案】

B

 

18．起重机将质量为 200 kg、静置于地面的货箱以 0.5 m/s² 的加速度匀加速竖直向上提升 5 s，g 取10 m/s²。求：

（1）此过程牵引力的平均功率；

（2）5 s 时牵引力的瞬时功率。

【答案】

（1）P = 2 625 W

（2）P = 5 250 W

【解析】

（1）由牛顿第二定律知 F_合 = ma = 200×0.5 N = 100 N。

分析货箱受力情况知，其所受合外力 F_合 = F − mg，所以 F = F_合 + mg = （100 + 2 000）N = 2 100 N。

在由静止开始匀加速 5 s 的过程中，位移 s = \(\frac{1}{2}\)at² = \(\frac{1}{2}\)×0.5×5² m = 6.25 m，牵引力做功 W = Fs = 2 100×6.25 J = 13 125 J，平均功率 P = \(\frac{W}{t}\) = \(\frac{13125}{5}\) W = 2 625 W

（2）5 s 时货箱速度 v = at = 0.5×5 m/s = 2.5 m/s，牵引力的瞬时功率 P = Fv = 2 100×2.5 W = 5 250 W

 

19．一辆额定功率为 50 kW、质量为 2 000 kg 的汽车，沿水平路面从静止开始行驶，它所受的阻力恒定为 2×10³ N。若汽车以额定功率行驶，求：

（1）当汽车的速度达到 5 m/s 时，汽车的加速度；

（2）汽车所能达到的最大速度。

【答案】

（1）a = 4 m/s²

（2）v_amx = 25 m/s

【解析】

在水平路面行驶的汽车所受合外力 F_合 = F − F_阻，其中阻力 F_阻 = 2×10³ N，牵引力 F 的功率 P = Fv。

（1）当汽车的速度达到 5 m/s 时，F = \(\frac{P}{v}\) = \(\frac{{5 \times {{10}^4}}}{5}\) N = 10 000 N，F_合 = F − F_阻 = （10 000 − 2 000）N = 8 000 N，由牛顿第二定律 F_合 = ma 知，a = \(\frac{F_合}{m}\) = \(\frac{8000}{2000}\) m/s² = 4 m/s²

（2）由 P = Fv 知，当汽车功率保持为额定功率时，随着速度的增加，牵引力减小，合外力减小，加速度减小，汽车做加速度减小的变加速运动。

当牵引力减小至等于阻力时，加速度减小为零，汽车达到最大速度 v_max。

有 F = F_阻 = 2×10³ N，v_amx = \(\frac{P}{v}\) = \(\frac{{5 \times {{10}^4}}}{2000}\) = 25 m/s

 

20．一个正在冲刺的百米赛跑运动员的动能最接近（    ）。

A．30 J                B．300 J               C．3 000 J                   D．30 000 J

【答案】

C

 

21．单个氧气分子质量为 5.31×10⁻²⁶ kg，若室温下氧气分子的平均动能约为 6.21×10⁻²¹ J，据此可估算室温下氧气分子的平均速率约为__________m/s。

【答案】

484

 

22．质量均为 1 400 kg 的汽车甲、乙、丙在公路上匀速行驶。已知甲车向东行驶的车速为 80 km/h，乙车向西行驶的车速为 80 km/h，丙车向南行驶的车速为 100 km/h，则甲、乙两车的动能________（选填“相同”或“不同”），甲、丙两车的动能之比为________。

【答案】

相同，16∶25

 

23．如图所示，足球守门员发球门球时，将质量为 0.4 kg、静止在草地上的足球以 10 m/s 的速度踢出，这时足球获得的动能是__________J。若踢出后足球沿草地做直线运动，受到的阻力是足球重力的 \(\frac{1}{5}\)，当足球运动到距发球点 20 m 的后卫队员处时，动能为_______J。（g 取10 m/s²）

【答案】

20，4

 

24．若质量为 1500 kg 的汽车的速度由 10 km/h 加速到 20 km/h，或由 50 km/h 加速到 60 km/h，通过计算说明，哪种情况汽车动能增加得比较多？

【答案】

根据动能定义 E_k = \(\frac{1}{2}\)mv²，速度由 10 km/h 加速到 20 km/h，动能约增加1.74×10⁴ J；而由 50 km/h 加速到 60 km/h，动能约增加 6.37×10⁴ J。由此可知，从 50 km/h 加速到 60 km/h 动能增加得多。

 

25．质量为 145 g 的棒球以 32 m/s 的速度撞上接球手的手套后移动 25 cm 才停止运动。求此过程中手套对棒球平均作用力的大小？

【答案】

296.96 N

【解析】

忽略棒球所受其他作用力，考虑棒球受手套作用力作用减速至零的过程，根据动能定理 W_合 = ΔE_k，有 − Fs = 0 − \(\frac{1}{2}\)mv²，故 F = \(\frac{{m{v^2}}}{{2s}}\) = \(\frac{{0.145 \times {{32}^2}}}{{2 \times 0.25}}\) N = 296.96 N。

 

26．水平地面上质量 m = 2 kg 的木块在水平向右的恒力 F = 4 N 作用下由静止开始运动。如木块和地面间的动摩擦因数 μ 为0.1，g 取 10 m/s²，则由静止开始运动的前 3 s 内，恒力 F 所做的功为________J，木块的末动能为_______J。

【答案】

18，9

 

27．为了汽车行驶的安全，车与车之间必须保持一定的距离。因为从驾驶员看见某一紧急情况到采取制动动作的时间里，汽车仍然要通过一段距离（称为思考距离）；而从采取制动动作到车完全停止的时间里，汽车又要通过一段距离（称为制动距离）。下表给出了不同车速下的思考距离和制动距离等部分数据。请分析这些数据，完成表格。

速度 v / (km·h−1)	思考距离 s1 / m	制动距离 s2 / m	停车距离 s3 / m
45	9	14	23
75	15	39
90
105	21	76	97

【答案】

54，18，56，74

 

28．节能混合动力车是一种可以利用汽油及所储存电能作为动力来源的汽车。质量 m = 1 000 kg的混合动力轿车，在平直公路上以 v₁ = 90 km/h 匀速行驶，发动机的输出功率为 P = 50 kW。当驾驶员看到前方有 80 km/h 的限速标志时踩下刹车，此时发动机功率不变，轿车立即启动利用电磁阻尼带动的发电机给电池充电，同时使轿车做减速运动，运动距离 L = 72 m后，速度变为 v₂ = 72 km/h，此过程中发动机功率的 \(\frac{1}{5}\) 用于轿车的牵引，\(\frac{4}{5}\) 用于供给发电机工作，发动机输送给发电机的能量中有 50% 转化为电池的电能。假设轿车在上述运动过程中所受阻力保持不变。求：

（1）轿车以 90 km/h 在平直公路上匀速行驶时，所受阻力 F_阻 的大小；

（2）轿车从 90 km/h 减速到 72 km/h 过程中，获得的电能 E_电；

（3）轿车仅用其在上述减速过程中获得的电能 E_电 维持 72 km/h 匀速运动的距离 L′。

【答案】

（1）F_阻 = 2×10³ N

（2）E_电 = 6.3×10⁴ J

（3）L′ = 31.5 m

【解析】

（1）汽车牵引力与输出功率的关系 P = F_牵v，将P = 50 kW，v₁ = 90 km/h = 25 m/s，代入得 F_牵 = \(\frac{P}{v_1}\) = 2×10³ N，当轿车匀速行驶时，牵引力与阻力大小相等，有 F_阻 = 2×10³ N。

（2）在减速过程中，发动机只有 \(\frac{1}{5}\)​​​​​​​P 用于汽车的牵引，根据动能定理有 \(\frac{1}{5}\)​​​​​​​Pt − F_阻L = \(\frac{1}{2}\)mv₂² − \(\frac{1}{2}\)​​​​​​​mv₁²，代入数据得 Pt = 1.575×10⁵ J，电源获得的电能为 E_电 = 0.5×\(\frac{4}{5}\)​​​​​​​Pt = 6.3×10⁴ J。

（3）根据题意，轿车在平直公路上匀速行驶时受到的阻力仍为 F_阻 = 2×10³ N，此过程中，由能量转化及守恒定律可知，仅有电能用于克服阻力做功 E_电 = F_阻L′，代入数据得 L′ = 31.5 m。

 

29．质量为 1.2 kg 的砖块在 16 m 高的楼顶处所具有的重力势能是_______J。（默认以地面为零势能面，g 取10 m/s²）

【答案】

192

 

30．在搬运货物上楼的过程中，重力对货物________（选填“做正功”“做负功”或“不做功”），货物的重力势能__________（选填“增大”“减小”或“不变”）。

在同一水平面内搬运货物的过程中，重力对货物_________（选填“做正功”“做负功”或“不做功”），货物的重力势能_________（选填“增大”“减小”或“不变”）。

在搬运货物下楼的过程中，重力对货物_______（选填“做正功”“做负功”或“不做功”），货物的重力势能_________（选填“增大”“减小”或“不变”）。

【答案】

做负功，增大，不做功，不变，做正功，减小

 

31．一个质量为 0.5 kg、尺寸为 200 mm×30 mm×10 mm的笔盒，从离地面 1.50 m 高的书架顶层落到地上。若以 1 m 高的桌面为零势能面，笔盒在书架上时的重力势能为_______J，笔盒在地上时的重力势能为_______J，下落过程的重力势能变化量为_______J。

若以地面为零势能面，笔盒在书架上时的重力势能为________J，笔盒在地上时的重力势能为________J，下落过程的重力势能变化量为________J。（g 取10 ms/²）

【答案】

2.5，− 5，−7.5，7.5，0，− 7.5

【解析】

此处笔盒高度 0.01 m，可认为远小于题中高度 1.5 m，计算中忽略尺寸对重心的影响；教师可对比竖直放置的书重心 0.1 m 则需纳入考虑的情况

 

32．一个长 3 m、宽 2 m、深 1.5 m的水池灌满了水。如把水全部放空流到与池底同高的地面，水的重力势能减少_______J。（水的密度为 1×10³ kg/m³，g 取 10 m/s²）

【答案】

6.75×10⁴

 

33．早晨，小华同学从五楼的家中出发，经过地下 5 m 深处的过街地道，来到街对面的学校二楼教室，全程路程为 800 m，则此过程中小华的重力势能最大值为_______J，最小值为_________J，重力对他做的功为__________J。（以地面为零势能面，小华质量 60 kg，所住楼房层高 3 m，学校教学楼层高 4 m，g 取10 m/s²）

【答案】

7 200，− 3 000，4 800（忽略小华身高的影响）

或7 740，− 2 460，4 800（考虑小华身高 1.8 m，则重心高度为 0.9 m；学生做出合理估值均为正确）

 

34．重力势能是________（选填“标量”或“矢量”），E_p1 = + 5 J、E_p2 = − 10 J，则 E_p1 ____ E_p2（选填“>”“=”或“<”）。

【答案】

标量，>

 

35．如图所示，质量为 m、长度为 l 的均匀柔软细绳 PQ 竖直悬挂。用外力将绳的下端 Q 缓慢地竖直向上拉起至点 M，点 M 与绳的上端 P 相距 \(\frac{l}{3}\)。在此过程中，绳的重力势能变化量为___________。

【答案】

\(\frac{1}{9}\)mgl

 

36．已知子弹的质量约为 5 g，飞行速度约为 500 m/s。以地面为重力势能零势能面，估算质量为 2 kg 的砖块在几层楼处具有和子弹动能相等的重力势能？（楼房层高以 3 m 计，g 取10 m/s²）

【答案】

约为11层

【解析】

根据已知条件知，子弹具有动能 E_k = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\)×0.005×500² J = 625 J。

重力加速度取 10 m/s²，砖块的重力势能 E_p = mgh = E_k，有 2×10 h = 625，所以 h = \(\frac{{{E_k}}}{{mg}}\)= \(\frac{{625}}{{2 \times 10}}\) m = 31.25 m，又 h = 31.25 m = 3 m×10 + 1.25 m，约为11层楼的对应高度（教师可引导学生注意高空坠物的危害）

 

37．估算 1 kW·h 的电能能将一位高中生托起多高。（g 取10 m/s²）

【答案】

7 200 m

【解析】

首先将电能单位转化为焦耳，1 kW·h = 3.6×10⁶ J。

重力加速度取 10 m/s²，假设高中生质量 m = 50 kg，将其举高 h，需做功 W = mgh。

所以 h = \(\frac{{{W}}}{{mg}}\) = \(\frac{{3.6 \times {{10}^6}}}{{50 \times 10}}\) m = 7 200 m

 

38．一人身高 1.8 m，质量为 70 kg，站立时摸高 2.3 m，跳起时摸高 2.9 m。选取地面为重力势能零势能面。忽略跳跃过程中姿态变化对人体重心的影响。若认为人保持正立姿态时重心在身高的一半处，则此人跳到最高时的重力势能值为多少？在立定跳高过程中重力势能最多增加了多少？（g 取10 m/s²）

【答案】

1 050 J，420 J

【解析】

人跳到最高时，重心在身高的一半处，其高度 h = （2.9 − 2.3 + 1.8×\(\frac{1}{2}\)）m = 1.5 m，重力势能值 E_p = Δmgh = 70×10×1.5 J = 1 050 J。

立定跳高过程中重心最高提升 Δh = （2.9 − 2.3）m = 0.6 m，所以重力势能最多增加 mgΔh = 70×10×0.6 J = 420 J。

 

39．__________和__________统称为机械能；_____________________的物体系统内，动能与势能相互转化，机械能守恒。

【答案】

动能，势能，只有重力和弹力做功

 

40．如果合力对物体做正功，物体的动能将_________；如果物体克服合力做功，物体的动能将__________；如果重力对物体做正功，物体的重力势能将__________；物体克服重力做功，物体的重力势能将___________。（均选填“增大”“减小”或“不变”）

【答案】

增大，减小，减小，增大

 

41．从距离地面 30 m 的高处自由落下一个小球，取地面为重力势能零势能面，当小球的高度为_______m 时，它的动能等于重力势能；当高度为_______m 时，它的动能等于重力势能的一半。

【答案】

15，20

 

42．在蹦极运动中，蹦极者在重力和弹性绳拉力的作用下下坠，反弹，再下坠，反弹……分析蹦极过程中各种能量的转化并补充填写下表。

能量的种类	具有能量的物体
动能	蹦极者
简述能量的转化

【答案】

能量的种类	具有能量的物体
动能	蹦极者
重力势能	蹦极者、地球系统
弹性势能	弹性绳系统
简述能量的转化
下坠过程首先是一段自由落体运动，重力势能转化为动能；绳拉直后先加速再减速至零，加速过程中重力势能转化为动能和弹性势能，减速过程中重力势能和动能转化为弹性势能。上升过程先加速再减速至零，加速过程中弹性势能转化为动能和重力势能，减速过程中弹性势能和动能转化为重力势能；上升过程中可能出现绳松弛的减速上升动能转化为重力势能的过程

 

43．沿斜面上滑的物体 A，其机械能 E_总 等于动能 E_k 与重力势能 E_p 之和。取地面为重力势能零势能面，该物体的 E_总 和 E_p 随它离开地面的高度 h 的变化如图所示。由图中数据可求得物体的质量为______kg，当 h = 0 时物体的速率为_______m/s，从地面升至 h = 4 m 的过程中物体的动能增量为_________J。（g 取 10 m/s²）

【答案】

2，10，− 100

 

44．关于重力势能，下述说法中正确的是（    ）。

A．物体具有的跟它的形变有关的能量叫重力势能

B．重力对物体做正功，物体的重力势能不一定减小

C．根据重力对物体所做的功，可以知道该重力势能的变化

D．重力不做功，其他力做功，物体的重力势能也可能变化

【答案】

C

 

45．如图所示，质量为 m 的小球从桌面竖直向上抛出，桌面离地高度为 h₁，小球能达到的最大离地高度为 h。若以桌面作为重力势能的参考平面，不计空气阻力，那么小球落地时的机械能为（    ）。

（A）mgh                    （B）mgh₁

（C）mg（h ＋ h₁）      （D）mg（h － h₁）

【答案】

D

 

46．如图所示，两个质量不同的物体A和B，分别从两个相同高度的光滑斜面和光滑圆弧形斜坡的顶点，从静止开始下滑到底部，以下说法正确的是（    ）。

（A）下滑过程中重力做的功相等            （B）它们在顶点时的机械能相等

（C）它们到达底部时的动能相等            （D）它们到达底部时的速度大小相等

【答案】

D

 

47．某同学身高 1.8 m，在运动会上他参加跳高比赛时采取背越式跳法，恰能越过 1.8 m 高的横杆。忽略他的水平速度，试估算该同学起跳时竖直向上的初速度大小，并简述理由。（g 取 10 m/s²）

【答案】

4.24 m/s

【解析】

该同学采取背越式跳法，可认为在越过 1.8 m 高的横杆过程中，重心的最大高度即为 H = 1.8 m，估计直立姿态起跳时其重心在身高一半高度 h₀ = 0.9 m。忽略阻力的影响和水平速度，在起跳到越过横杆的过程中，仅受重力作用，机械能守恒。选择地面为零势能面，有 \(\frac{1}{2}\)mv² + mgh₀ = 0 + mgH，代入数值即可知初速度大小约为 4.24 m/s。

 

48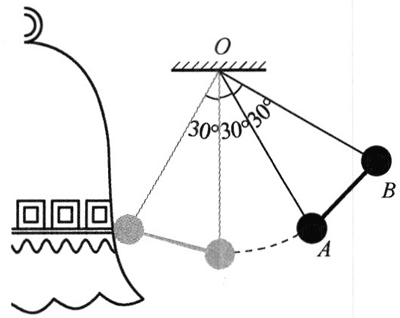．如图所示，两个质量均为 m 的重锤用不计质量的细杆 AB 连接，轻绳长度 OA = OB = L，它们之间的夹角为 30°。开始时OA偏离竖直方向 30° 由静止开始下落。当左边的重锤碰到钟时，右边的重锤恰好在最低点，即 OB 恰好在竖直方向。求重锤碰到钟时的速度大小。

【答案】

\(\sqrt {\frac{{gL}}{2}} \)

【解析】

重锤整体由静止开始下落至即将击中钟的过程中，仅有重力对系统做功，系统机械能守恒。

将重锤摆动的最低点（即图中 B′ 点）设为零势能面，根据机械能守恒定律，有0 + 0 + mgh_A + mgh_B = \(\frac{1}{2}\)mv_A² + \(\frac{1}{2}\)mv_B² + mghʹ_A + 0。

又 v_A = v_B 令为 v，h_A = L（1 − cos30°），h_B = L（1 − cos 60°），h'_A = L（1 − cos30°），代入可得 mgL（1 − cos30°） + mgL（1 − cos60°） = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)mv² + mgL（1 − cos30°）。

整理得 v = \(\sqrt {gL(1 - \cos 60^\circ )} \) = \(\sqrt {\frac{{gL}}{2}} \)。