1．在物理学中，把物体沿______________运动叫曲线运动；曲线运动的速度方向是不断改变的，物体瞬时速度的方向沿______________方向。

【答案】

曲线所做的，曲线的切线

 

2．做曲线运动物体的速度方向是不断改变的，故物体的加速度与速度不在___________上；根据牛顿第二定律，物体做曲线运动的条件是：物体受到的合力与____________________________。

【答案】

同一直线，物体速度方向不在同一直线上2

 

3．判断以下关于曲线运动的说法是否正确并说明理由。

说法	判断	说明理由或举例
变速运动动一定是曲线运动
曲线运动一定是变速运动
曲线运动可以是匀变速运动

【答案】

错，匀加速直线运动也是变速运动

对，曲线运动的速度方向一定变化

对，曲线运动速度方向变化但其加速度可以不变

 

4．下列关于物体做曲线运动与受力情况的说法中正确的是（    ）。

A．物体在变力作用下一定做曲线运动

B．物体在恒力作用下不可能做曲线运动

C．做曲线运动的物体所受合力的方向一定是变化的

D．做曲线运动的物体所受合力的方向与速度方向一定不在同一条直线上

【答案】

D

 

5．质点做曲线运动，依次经过 A、B、C 三点的速度分别为 v_A、v_B、v_C，受到合力分别为 F_A、F_B、F_C，上述各物理量方向如图所示，其中一定不正确的有___________。

【答案】

v_B、F_B

 

6．在教材第 3 页的“吹乒乓球”自主活动中，若某同学在桌子边缘垂直于乒乓球运动方向，正对着“指定位置”用力吹滚来的乒乓球，但乒乓球总是到不了“指定位置”。分析其中的原因。 

【答案】

吹乒乓球时，对乒乓珠侧向施力，使乒乓球产生一侧向加速度，开始做曲线运动而转弯。但在原运动方向上，乒乓球由于惯性仍然要保持原有的分速度而继续运动，所以乒乓球到不了指定位置。

 

7．如图所示，洋山港大型集装箱吊车在 10 s 内沿水平方向匀速移动 50 m 的同时，将所吊的货箱匀速放下 10 m，则货箱的位移大小为_________m，其速度的竖直分量大小为___________m/s。

【答案】

s ≈ 51 m，v_y = 1 m/s

 

8．如图所示，机动小船在静水中的行驶速度为 5 m/s。若它在流速为 1 m/s 的河水中行驶，且行驶时船头对准与河岸垂直的方向，求小船相对于河岸的速度的大小与方向。

【答案】

v ≈ 5.10 m/s，θ 为78.7°。

 

9．用于航空测量的无人机（在静止空气中）的飞行速度为 90 km/h，现执行自 A 处向正北方向的 B 处飞行的任务，A、B 两处相距 500 m。有风自西向东吹来，风速为 6 m/s。问：

（1）为使无人机能直线飞行抵达 B 处，机头应对准什么方向飞行？飞行需多少时间？

（2）若当无人机机头对准正北方向飞行时，能使它飞抵位于 B 处正东方向的 C 处，则 B、C 两处的距离是多少？自 A 处飞抵 C 处需多少时间？

【答案】

（1）向北偏西13.9°方向飞行；v ≈ 24.27 m/s，飞行时间 t = 20.6 s。

（2）B、C 距离 d = 120 m；飞行时间 t = 20 s。

 

10．以一定初速度抛出的实心球，在只受________作用条件下所做的运动叫做抛体运动。所以抛体运动的加速度为_________________，是一种_________曲线运动。

【答案】

重力，重力加速度（或 9.8 m/s²），匀变速

 

11．复杂的曲线运动一般可以用运动_________与_________的方法进行研究。通过实验探究可知，平抛运动可以分解为水平方向的____________运动和竖直方向的____________运动。

【答案】

合成，分解，匀速直线，自由落体

 

12．图为研究平抛运动的两个实验装置示意图。如图（a）所示，用小锤击打金属片，A 球水平飞出做平抛运动的同时，B 球做自由落体运动，两球同时落地；如图（b）所示，小球 C、D 被同时释放后沿相同轨道运动，当 C 球自轨道 M 处水平飞出做平抛运动的同时，D 球恰好从轨道 N 处进入光滑水平面并做直线运动，两球最终在水平面上相碰。图（a）实验表明：____________________________________________________；图（b）实验表明：___________________________________________。

【答案】

平抛运动竖直方向的分运动为自由落体运动，平抛运动水平方向的分运动为匀速直线运动（此题（b）图好像没说清楚，P、A、Q、B也没交代）

 

13．物体做平抛运动的过程中，在连续相等的时间间隔内，下列物理量哪些是相等的、哪些不相等？说明理由。

A．位移        B．平均速度        C．速度的变化量        D．加速度

【答案】

因为做平抛运动的物体在连续相等时间内位移的大小和方向都是变化的，所以选项 A、B 错误；而平抛运动物体的加速度为重力加速度 g，所以选项 D 正确；在相等时间 Δt 内 Δv = gΔt，速度的变化量相等，所以选项 C 正确。

 

14．一玩具手枪自水平地面上方某处水平射出一颗弹丸 A，同时另一弹丸 B 从同一高度自由下落。判断以下说法是否正确并简述理由。

说法	判断	说明理由或举例
弹丸 A 先落地
弹丸 B 通过的位移较小
两弹丸落地时的速率可能相等
两弹丸落地过程中速度的变化量相等
两弹丸在空中运动的加速度相同

【答案】

错，平抛运动的竖直分运动为自由落体运动，根据分运动与合运动的等时性，两者同时落地

对，平抛运动位移的竖直分量是自由落体的位移

错，平抛运动末速度的竖直分量是自由落体的末速度

对，两者运动的加速度均为竖直向下的重力加速度 g

对，两者运动的加速度均为竖直向下的重力加速度 g

 

15．A、B 两物体都做平抛运动，它们的初始位置离地高度分别为 \(\frac{h}{3}\) 和 h，初速度之比为 3∶2，则它们落至地面前的飞行时间之比为____________，水平方向的位移之比为_________；落地时，水平方向的速度分量之比为___________，竖直方向的速度分量之比为___________。

【答案】

1∶\(\sqrt 3 \)，\(\sqrt 3 \)∶2，3∶2，1∶\(\sqrt 3 \)

【解析】

根据平抛运动竖直方向、水平方向的位移和速度表达式可得上述答案。

 

16．A、B、C、D 四个小球分别从不同的高度以不同的初速度水平抛出。根据下表判断落地时哪个小球的瞬时速度与竖直方向之间的夹角最大，并说明理由。

小球	A	B	C	D
高度 h / m	5	5	10	10
初速度 v / (m·s−1)	5	10	5	10

【答案】

根据 tanθ = \(\frac{{{v_0}}}{{{v_y}}}\) 可得，初速度相同时，高度越小，小球落地的瞬时速度与竖直方向之间的夹角越大；同一高度抛出时，初速度越大，小球落地的瞬时速度与竖直方向之间的夹角越大，因 B 球的高度小且初速度大，所以 B 球落地的瞬时速度与竖直方向的夹角最大。

 

17．如图所示，一游客在比水面高出 70 m 的陡峭悬崖边上以 10 m/s 的速度水平抛出一颗石子。

（1）能否将这颗石子的运动近似看成平抛运动，简述近似条件。

（2）若近似条件成立，估算这颗石子的落水点与抛出点的水平距离以及落入河水时的速度。

【答案】

（1）当风速不大时，忽略空气阻力的情况下，石子的运动可以看成平抛运动。

（2）v ≈ 38.33 m/s，速度方向与竖直方向的夹角约为 15.1°。

【解析】

（2）平抛运动的时间 t = \(\sqrt {\frac{{2h}}{g}} \) = \(\sqrt {\frac{{2 \times 70}}{{9.8}}} \) s ≈ 3.78 s；水平距离 x = v₀t = 10×3.78 m =37.8 m；因为 v_y = \(\sqrt {2gy} \) = \(\sqrt {2 \times 9.8 \times 70} \) m/s ≈ 37.04 m/s，得石子入水瞬时速度大小 v = \(\sqrt {v_0^2 + v_y^2} \) = \(\sqrt {{{10}^2} + {{37}^2}} \) ≈ 38.33 m/s，

由 tanθ = \(\frac{{{v_0}}}{{{v_y}}}\) = \(\frac{{10}}{{37}}\) ≈ 0.27，可得速度方向与竖直方向的夹角约为 15.1°。

 

18．如图所示，某两层观景平台的高度分别为 h₁ = 1.95 m和 h₂ = 1.25 m，第一层平台的宽度为 l = 1.5 m。现以 v₀ = 4 m/s 的初速度从第二层平台边缘水平推出一小球，忽略空气阻力，g 取 10 m/s²，则小球将落在何处？

【答案】

落在第一层平台下 1.7 m 远的地面上。

【解析】

小球下落 h₂ 过程的水平位移 x = v₀\(\sqrt {\frac{{2{h_2}}}{g}} \) = 2 m > l，故小球不会落到第一层平台上，而是直接落到地面。小球落到地面的水平位移 xʹ = v₀\(\sqrt {\frac{{2({h_1} + {h_2})}}{g}} \) = 3.2 m，设 lʹ = xʹ − l = (3.2 − 1.5) m = 1.7 m，则小球落在第一层平台下 1.7 m 远的地面上。

 

19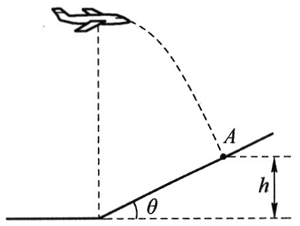．如图所示，飞机沿水平方向匀速飞行，到达山坡底端正上方时释放一颗炸弹，炸弹垂直击中山坡上的目标 A。已知 A 点高度为 h，山坡倾角为θ。求飞机飞行的速度大小和飞行高度。

【答案】

v₀ = \(\sqrt {gh} \)；H = h\(\left( {1 + \frac{1}{{2{{\tan }^2}\theta }}} \right)\)

【解析】

设竖直方向的速度分量为 v_y，由题意，tanθ = \(\frac{{{v_0}}}{{{v_y}}}\) = \(\frac{h}{x}\)，x = v₀t，v_y = gt，可解得 v₀ = \(\sqrt {gh} \)；

因为 v_y = \(\sqrt {2gy} \) = \(\frac{{{v_0}}}{{\tan \theta }}\) = \(\frac{{\sqrt {gh} }}{{\tan \theta }}\)，得 y = \(\frac{h}{{2{{\tan }^2}\theta }}\)，所以飞行高度 H = h + y = h\(\left( {1 + \frac{1}{{2{{\tan }^2}\theta }}} \right)\)。

 

20．如图所示，一倾角为 θ 的斜面，长为 m，宽为 n，其顶边与底边平行。某人从 P 点沿斜面的顶边抛出一个小铁球，斜面对铁球的阻力可忽略不计。

（1）分析说明，该小铁球在斜面上做何种运动？

（2）若小铁球恰能从底边的端点 Q 处离开斜面，则小铁球抛出的初速度 v₀ 应为多大？

【答案】

（1）做类似平抛运动的匀变速曲线运动。

（2）v₀ = n\(\sqrt {\frac{{g\sin \theta }}{{2m}}} \)

【解析】

（1）对小铁球受力分析可得，它受到的合力沿斜面向下，与初速度方向垂直，所以小铁球做类似平抛运动的匀变速曲线运动。

（2）小铁球的运动加速度为 a = gsinθ，在斜面上运动的时间 t = \(\sqrt {\frac{{2m}}{a}} \) = \(\sqrt {\frac{{2m}}{{g\sin \theta }}} \)，则初速度大小 v₀ = \(\frac{n}{t}\) = n\(\sqrt {\frac{{g\sin \theta }}{{2m}}} \)。

 

21．物体沿_______________所做的运动就是圆周运动。如果做圆周运动的物体在任意相等时间里通过的__________相等，这种运动就叫做匀速圆周运动。

【答案】

圆周，弧长（或路程）

 

22．质点做匀速圆周运动时，线速度大小__________，方向不断改变，所以匀速圆周运动实质是速度___________的运动。（均选填“不变”或“变化”）

【答案】

不变，变化2

 

23．汽车以恒定速率在广场上做匀速圆周运动，每 2 min 行驶一圈。汽车每行驶半圈，初、末速度的夹角为____________；每过 10 s，汽车初、末速度的夹角为_____________。在图中画出汽车经过点 A 时及此后 10 s 所在位置的速度矢量方向。（已知汽车顺时针方向行驶）

【答案】

180°，30°。见图

 

24．判断下列关于匀速圆周运动的说法是否正确，说明理由。

说法	判断	说明理由或举例
因为匀速圆周运动是匀速运动，所以速度不变
因为匀速圆周运动是曲线运动，所以是变速运动
做匀速圆周运动的物体线速度越大，则运动一周的时间越短
做匀速圆周运动的物体，角速度越大，则运动一周的时间越短

【答案】

错，匀速圆周运动的速度大小不变，但方向时刻改变，所以速度是变化的

对，曲线运动的速度方向时刻在变，所以是变速运动

错，因为 T = \(\frac{{2\pi r}}{v}\)，所以仅凭线速度大还不能判定周期小

对，因为 T = \(\frac{{2\pi }}{\omega }\)，所以角速度越大，即可断定周期越小，即运动一动一周的时间越短

 

25．甲、乙两人分别沿半径为 12 m 和 15 m 的圆形跑道匀速率跑步，设甲、乙的线速度分别为 v₁、v₂；角速度分别为 ω₁、ω₂；周期分别为 T₁、T₂。比较以下情况中上述各物理量的大小。

序号	运动情况	运动快慢的比较
（1）	甲用 10 s跑完一圈，乙用 12 s 跑完一圈	v1 ______ v2，ω1 ________ ω2，T1 ________ T2
（2）	两人同时跑完一圈	v1 ______ v2，ω1 ________ ω2，T1 ________ T2
（3）	两人以相同的速率各自跑完一圈	v1 ______ v2，ω1 ________ ω2，T1 ________ T2

【答案】

（1）＜，＞，＜

（2）小于，=，=

（3）=，＞，＜

 

26．质点 A、B 均做匀速圆周运动，若相同时间内它们通过的弧长之比 s_A∶s_B = 2∶3，绕圆心转过的角度之比 ω_A∶ω_B = 3∶2，则它们的线速度大小之比 v_A∶v_B = ______，周期之比T_A∶T_B = _______，半径之比 R_A∶R_B = _______。

【答案】

2∶3，2∶3，4∶9202

 

27．关于一个做匀速转动的物体，判断下列说法是否正确并说明理由。

说法	判断	说明理由或举例
物体上任何一点的线速度都不变
物体上任何一点的角速度都不变
物体上任意两点的线速度大小都不同
物体上任意两点的角速度大小都不同

【答案】

错，匀速转动物体上的每一点都在做匀速圆周运动，线速度时刻改变

对，匀速转动物体上的每一点都在做匀速圆周运动，角速度保持不变

错，半径相同的点，线速度大小都相同

错，匀速转动物体上的每一点做圆周运动的角速度都相同

 

28．图为一皮带传动装置示意图，右轮的半径为 r，a 是它边缘上的一点。左轮是一个轮轴，轮半径为 4r，轴半径为 2r。点 b 在轴上，到轴心的距离为 r，点 c 和点 d 分别在轴和轮的边缘。若传动过程中皮带不打滑，a、b、c、d 四点中，线速度大小相同的是_________，角速度大小相同的是_________。

【答案】

a 和 c，b、c 和 d

【解析】

因为皮带不打滑，所以 a、c 两点的线速度大小均与皮带速度相同，而 b、c、d 为绕轴转动的同一物体上的三个点，所以角速度大小相同。

 

29．设汽车在公路上行驶时不打滑，车轮每转一周，汽车向前行驶的距离等于车轮的周长。某轿车的车轮半径为 30 cm，当该轿车在高速公路上行驶时，驾驶员面前的速率计的指针指在“120 km/h”上，求此时车轮的转速。

【答案】

n ≈17.69 r/s

【解析】

速率计的指针指在“120 km/h”上，表示此刻汽车的行驶速率为 120 km/h ≈ 33.33 m/s。车轮轮缘上的点绕轮轴转动的线速度大小就等于汽车行驶的速率，为 33.33 m/s。根据 n = \(\frac{\omega }{{2\pi }}\) = \(\frac{v}{{2\pi r}}\)，可求出 n ≈17.69 r/s。

 

30．物体做圆周运动时受到向心力的作用，则：

（1）向心力的方向：总是____________，不断变化；

（2）向心力是根据____________来命名的，向心力可以是重力、弹力或摩擦力以及它们的合力；

（3）向心力的作用效果：产生______________，不断改变线速度的___________；

（4）做匀速圆周运动的物体所受的合力全部用来提供__________________。

【答案】

（1）指向圆心

（2）作用效果

（3）向心加速度，方向

（4）向心力

 

31．判断下列关于向心力的说法是否正确，说明理由。

说法	判断	说明理由或举例
向心力的方向始终沿着半径指向圆心，所以是一个恒力
对做匀速圆周运动的物体进行受力分析时，不能遗漏向心力
向心力只改变物体运动的方向，不改变运动的快慢

【答案】

错，向心力的方向从物体指向圆心，物体的位置在变化，从不同的位置指向圆心的方向是变化的，所以向心力是变力

错，做匀速圆周运动的物体，受到的向心力是它所受力的合力

对，向心力与速度方向垂直，所以不改变速度的大小，只改变速度的方向

 

32．如图所示的传动装置中，两轮分别绕轴心 O₁、O₂ 做匀速转动，在图中标出轮子边缘上点 A 的速度方向和点 B 受到的向心力方向。

【答案】

如图

 

33．甲、乙两个物体均做匀速圆周运动。它们的质量之比为 1∶3，运动半径之比为 3∶1，当甲、乙的角速度之比为 2∶1 时，向心加速度大小之比为_______，向心力大小之比为________；当甲、乙的线速度之比为 2∶1 时，向心加速度大小之比为_________，向心力大小之比为__________。

【答案】

12∶1，4∶1，4∶3，4∶9。

【解析】

由 a = ω²r 可得 \(\frac{{{a_1}}}{{{a_2}}}\) = \(\frac{{\omega _1^2}}{{\omega _2^2}}\)·\(\frac{{{r_1}}}{{{r_2}}}\)；由 F = mω²r 可得 \(\frac{{{F_1}}}{{{F_2}}}\) = \(\frac{{{m_1}}}{{{m_2}}}\)·\(\frac{{\omega _1^2}}{{\omega _2^2}}\)·\(\frac{{{r_1}}}{{{r_2}}}\)；由 a = \(\frac{{{v^2}}}{r}\) 可得 \(\frac{{{a_1}}}{{{a_2}}}\) = \(\frac{{v_1^2}}{{v_2^2}}\)·\(\frac{{{r_2}}}{{{r_1}}}\)；由 F = m\(\frac{{{v^2}}}{r}\) 可得 \(\frac{{{F_1}}}{{{F_2}}}\) = \(\frac{{{m_1}}}{{{m_2}}}\)·\(\frac{{v_1^2}}{{v_2^2}}\)·\(\frac{{{r_2}}}{{{r_1}}}\)。

 

34．两个质量相同的物体分别静止放在北京和广州，均随地球一起运动。下列关于这两个物体运动的说法正确的是（    ）。

A．向心力大小相同                   B．向心加速度大小相同

C．角速度大小相同                   D．线速度大小相同

【答案】

C

【解析】

物体随地球自转而绕其自转轴做匀速圆周运动，角速度、周期由地球自转决定，所以，不论放在哪里，物体的角速度和周期都相同，所以选项 C 正确。在北京和广州的物体运动的半径不同，向心力 F = mω²r，所以向心力大小不同，选项 A 错误；向心加速度 a = ω²r，所以向心加速度大小不同，选项 B 错误；线速度 v = ωr，所以线速度大小不同，选项 D 错误。

 

35．如图所示，用一根细绳拴住质量为 m 的小球，当小球在水平面内做匀速圆周运动时，绳与竖直方向的夹角为 θ。

（1）小球受几个力的作用？

（2）小球受到的合力、向心力的方向。

【答案】

（1）两个力，重力和绳的拉力

（2）小球受到的合力提供向心力，由小球指向 Oʹ。

 

36．在一个半径为 2.25 m 的水平离心实验器中，一名航天员正在进行旋转训练。已知他的向心加速度是 8g（g 取10 m/s²）。求：

（1）航天员运动速度的大小；

（2）航天员运动的周期。

【答案】

（1）v ≈13.42 m/s

（2）T ≈ 1.05 s

【解析】

（1）根据 a = \(\frac{{{v^2}}}{r}\)，可解得 v = \(\sqrt {ar} \)，将 a = 8g、r = 2.25 m 代入，可解得 v ≈13.42 m/s

（2）根据 T = \(\frac{{2\pi r}}{v}\)，可解得 T ≈ 1.05 s

 

37．如图所示，在光滑水平面上相距 20 cm 的两处分别钉两个钉子 A 和 B，长为 1 m 的细绳一端系一质量为 0.4 kg 的小球，另一端固定在钉子 A 上，开始时小球与 A、B 在同一直线上。使小球以 2 m/s 的速率在水平面上做匀速圆周运动。如果细绳能承受的最大拉力为 4 N，问：小球运动多久以后细绳会被拉断？

【答案】

t  ≈ 3.77 s

【解析】

小球在运动过程中水平方向上只受到绳子拉力的作用，该力始终与小球速度方向垂直，不改变速度的大小，所以小球在运动中的速率始终是 2 m/s。当绳子拉力（即小球受到的向心力）达到 4 N 时，绳子将断，根据 F = m\(\frac{{{v^2}}}{r}\) 可求出细绳将断时小球的运动半径 r_min = m\(\frac{{{v^2}}}{{{F_{\max }}}}\)，代入已知数据可得 r_min = 0.4 m。根据题意可知，小球每运动半圈，运动半径减小20 cm，所以半径从 1 m 减小到 0.4 m 需经过 3 个半圈。根据 T = \(\frac{{2\pi r}}{v}\) 可求得 T₁ = π s，T₂ = 0.8π s，T₃ = 0.6π s。所以 t = \(\frac{{{T_1}}}{2}\) + \(\frac{{{T_2}}}{2}\) + \(\frac{{{T_3}}}{2}\) = 1.2π s ≈ 3.77 s。

 

38．图为自行车比赛中运动员经过弯道时的情境，提出一个与图示情境相关的物理问题并作出简要的分析和回答。

【答案】

问题（1）：自行车赛道转弯处的平面为什么都做成倾斜的？回答：赛道倾斜，自行车受到的弹力倾斜向上，其水平分力可以为自行车转弯提供所需的向心力。

问题（2）：对行驶在转弯道内侧的选手和外侧的选手而言，如果他们的质量相同，行驶速度大小相同，谁需要的向心力更大？回答：行驶在内侧赛道的选手需要的向心力更大。根据向心力公式 F = m\(\frac{{{v^2}}}{r}\) 可知，质量相同、速度大小相同的情况下，半径越小所需向心力越大。

 

39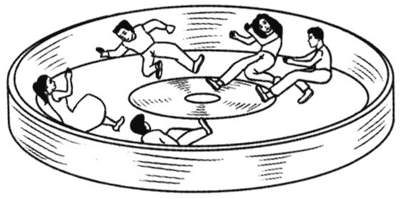．图是一种娱乐设施“魔盘”，两位同学观察图片后发生了争论。甲说：“图画错了，做圆周运动的物体受到向心力的作用，魔盘里的人应该是向中心靠拢。”乙说：“图没画错，因为旋转的魔盘给人离心力，所以人向盘边缘靠拢。”请你对两位同学的说法作出评价并简述理由。

【答案】

甲、乙两位同学的说法都不正确。向心力的作用效果是改变物体的运动方向，并不会使物体朝圆心运动，所以甲的说法错误。以地面为参考系来看，人向盘边缘靠拢是因为盘底给人的摩擦力不足以提供人做圆周运动所需的向心力，所以人做离心运动，而不是因为人受到了离心力的作用，所以乙的说法也不对。

 

40．图为一水平赛车跑道，其弯道为内、外半径分别为 r₁、r₂ 的 \(\frac{1}{4}\) 圆弧。甲、乙两赛车分别沿弯道最内侧和最外侧行驶，已知两赛车质量相同，两赛车与路面的最大静摩擦力也相同，则甲、乙转弯时最大安全速度之比为____________；甲、乙以最大安全速度完成转弯所用时间之比为________。

【答案】

\(\sqrt {{r_1}} \)∶\(\sqrt {{r_2}} \)，\(\sqrt {{r_1}} \)∶\(\sqrt {{r_2}} \)

【解析】

根据已知条件和 F = m\(\frac{{{v^2}}}{r}\) 可得，v₁∶v₂ = \(\sqrt {{r_1}} \)∶\(\sqrt {{r_2}} \)；根据 t = \(\frac{l}{v}\) 和 l = \(\frac{1}{2}\)πr 可得，t₁∶t₂ = \(\sqrt {{r_1}} \)∶\(\sqrt {{r_2}} \)。

 

41．如图所示，物块在水平圆盘上与圆盘一起绕固定轴匀速转动，判断下列说法是否正确，说明理由。

说法	判断	说明理由或举例
物块处于平衡状态
物块受到三个力作用
角速度一定时，物块距转轴的距离越远，越容易脱离圆盘
物块距转轴距离一定时，运动周期越小，越不容易脱离圆盘

【答案】

错，平衡状态中物体的速度大小、方向都不变，而圆盘上物块的速度方向不断变化，所以不是平衡状态

对，物块受到重力、支持力和静摩擦力的作用

对，根据向心力公式 F = mω²r，物块到转轴的距离越大，需要的向心力越大，越接近最大静摩擦力，即越容易脱离圆盘

错，周期越小即角速度越大，根据向心力公式 F = mω²r，角速度越大，需要的向心力越大，越接近最大静摩擦力，即越容易脱离圆盘

 

42．如图所示，铁路弯道处的内外轨道高低不同，已知内外轨道所在平面与水平面的夹角为 θ。火车在该弯道处沿半径为 R 的圆弧转弯时，建议火车的行驶速度是 \(\sqrt {Rg\tan \theta } \)。

（1）为什么建议速度是 \(\sqrt {Rg\tan \theta } \)？

（2）如果火车在这段弯道上转弯的速度不等于 \(\sqrt {Rg\tan \theta } \)，分析车轮的轮缘与内轨或外轨间挤压作用力的大小内与转弯速度的关系。

【答案】

（1）以建议的速度行驶时，火车受到的重力和垂直于轨道平面的支持力作用的合力恰好可以提供向心力，火车轮缘对内轨和外轨恰好无挤压作用，对轨道不会造成损害。

（2）如果火车转弯时的速度大于 \(\sqrt {Rg\tan \theta } \)，火车需要更大的向心力，轮缘会对外轨造成挤压，速度越大，挤压作用越大；如果速度小于 \(\sqrt {Rg\tan \theta } \)，火车需要的向心力较小，轮缘会对内轨造成挤压，速度越小，这个挤压作用越大。

 

43．图为一实验小车中利用光电脉冲测量车速和行程的装置示意图，A 为光源，B 为光电接收器，A、B 均固定在车身上，C 为小车的车轮，D 为与 C 同轴相连的齿轮。车轮转动时，A 发出的光束通过旋转齿轮上齿的间隙后变成脉冲光信号，被 B 接收并转换成电信号，由电子电路记录并显示。

若实验显示单位时间内 B 接收到的脉冲数为 n，累计接收脉冲数为 N，则要测出小车的速率和行驶路程还需测量哪些物理量？试由所有测量的物理量推导出小车的速率和行驶路程的表达式。

【答案】

还需要测量齿轮的齿数 p，以及车轮的半径 r。实验中小车齿轮转过的圈数为 \(\frac{N}{p}\)，则小车的行程 l = \(\frac{N}{p}\)·2πr = \(\frac{{2\pi rN}}{p}\)，小车行驶的时间 t = \(\frac{N}{n}\)，所以小车的速率 v = \(\frac{{2\pi rn}}{p}\)。

 

44．如图所示，一根轻绳穿过水平转台中心处的光滑小孔 O，一端与转台上光滑凹槽内的小球 A 相连，另一端连接物体 B，A 和 B 质量均为 1 kg。已知 O 与 A 相距 25 cm，开始时 B 与水平地面接触，转台转动过程中 A 始终随着它一起运动。那么，

（1）当转台以角速度 ω = 4 rad/s 旋转时，B 对地面的压力为多大？

（2）要使 B 脱离地面，则转台旋转的角速度至少为多大？（g 取 10 m/s²）

【答案】

（1）6 N

（2）ωʹ = 2\(\sqrt {10} \) rad/s

【解析】

（1）根据向心力公式 F = mω²r，可算出当小球 A 随转台以角速度 ω = 4 rad/s、半径 r = 0.25 m 转动时，所受向心力 F = 4 N。因为这个向心力由轻绳提供，所以轻绳对物体 B 的拉力 F_拉 = 4 N。物体 B 静止在地面上，受到重力、支持力和绳拉力的作用，根据共点力平衡有 mg = F_N + F_拉，即可求出地面对 B 的支持力 F_N = 6 N，所以 B 对地面的压力也为6 N。

（2）要使 B 脱离地面，则绳对 B 的拉力要等于 B 的重力，即 10 N，此时小球 A 受到的向心力也为 10 N。根据 F = mω²r，即可求得角速度至少为 ωʹ = 2\(\sqrt {10} \) rad/s。

 

45．如图所示，倒置的光滑圆锥内侧，有质量相同的两个小球 A、B 沿圆锥内侧在水平面内做匀速圆周运动。它们的角速度 ω_A ________ ω_B，线速度 v_A _______ v_B，向心加速度 a_A _______ a_B。（均选填“>”“<”或“=”）

【答案】

<，>，=

【解析】

小球受重力与圆锥壁弹力的作用，其合力即小球做匀速圆周运动的向心力。由重力的大小与方向以及弹力和向心力的方向，可得向心力 F = mgcotα（α 为半锥角），所以两小球的向心力相同。而两球做圆周运动的半径 r_A > r_B。根据 ω² = \(\frac{F}{{mr}}\) 可判定 ω_A < ω_B，根据 v² = \(\frac{Fr}{{m}}\) 可判定 v_A > v_B，根据 a = \(\frac{{Fr}}{m}\) 可判定 a_A = a_B。