1．力是物体间的__________，力有大小、方向和_______三个要素，可用有向线段来表示力。

【答案】

相互作用，作用点

 

2．物体所受重力G的施力物体是_______，其方向总是__________。重力的等效作用点称为重心，做伸展运动时，双侧手臂向上伸举，在此过程中，人的重心位置________（选填“固定不变”或“时刻变化”）。

【答案】

地球，竖直向下，时刻变化

 

3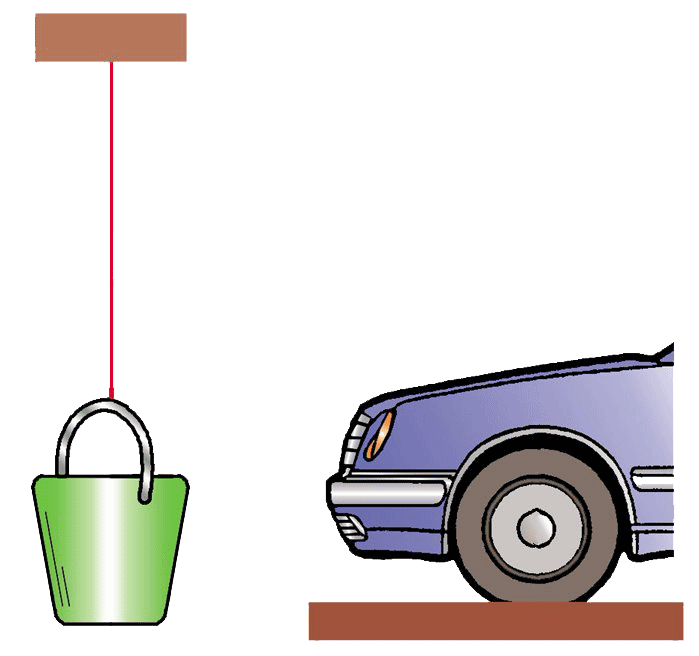．如图所示，桶的把手对绳的拉力和车轮对地面的压力就其性质而言均为弹力，因为它们分别是__________和__________发生弹性形变引起的。

【答案】

桶的把手，车轮

 

4．一轻质弹簧原长为8 cm，在4 N的拉力作用下伸长了2 cm，弹簧未超出弹性限度，则该弹簧的劲度系数为_______N/m。

【答案】

200

 

5．观察与了解生活中的哪些地方用到了弹簧，通过一个实例，说明弹簧的作用。

【答案】

生活中多处利用了弹簧，能举出合适的例子并予以说明即可。如圆珠笔中用到弹簧，写字时下压按钮，弹簧压缩，写字结束下压按钮，在弹簧的弹力作用下，笔尖缩回到笔中。

 

6．常用润滑油来减少门窗与轨道或转轴间的摩擦以方便开关。生活中有没有需要增加摩擦的情形？举例说明。

【答案】

鞋底、把手、轮胎表面有花纹都是为了增加摩擦，如果没有摩擦，人无法行走，手握不住东西，车辆无法制动。

 

7．相互接触的两个物体之间是否一定存在弹力？如图所示，质量均匀分布的小球静置于水平地面上，且与竖直墙面接触，其在A、B两处是否受到弹力？

【答案】

图中小球与竖直平面和水平地面的接触点分别为A、B。小球和水平面在B点都有形变，在A点没有发生形变，所以在B点小球对水平地面有压力，水平地面对小球有支持力，在A点不存在弹力。

 

8．重60 N的物体受到12 N的水平拉力作用，沿水平方向做匀速直线运动，物体与地面的动摩擦因数为_________；若运动时水平拉力增大到20 N，则地面对物体的摩擦力为_________。

【答案】

0.2，12 N。提示：因物体与地面间的压力不变，摩擦力也不变。

 

9．如图所示，标记为A的各物体质量均匀分布，图（a）、（b）、（c）、（d）中的物体A均处于静止状态。图（e）中的物体A沿着粗糙竖直墙面下滑，图（f）中的物体A被水平外力紧压在竖直墙面上，处于静止状态。在图上分别画出它们所受重力和弹力的示意图。

【答案】

如图所示

 

10．某同学有如下实验设想：

目的：测量木块与桌面间的动摩擦因数。

器材：弹簧测力计、方形木块。

对象：做匀速直线运动的木块。

步骤：

（1）为了测量木块所受重力G的大小，将木块竖直悬挂于弹簧测力计下端，读出木块________时弹簧测力计的示数F₁。

（2）用弹簧测力计水平拉动木块在水平桌面上做________运动，读出弹簧测力计的示数F₂。

结论：动摩擦因数μ =\(\frac{{{F_2}}}{{{F_1}}}\)

写出得出实验结论的分析过程。

【答案】

（1）静止

（2）匀速直线。由步骤（1）可知，悬挂的木块静止时，竖直方向所受的二力平衡，重力G与弹簧测力计拉力F₁大小相等。当木块在水平桌面上做匀速直线运动时，桌面对木块的弹力F_N大小等于木块所受重力的大小，等于F₁的大小。由步骤（2）可知，木块在水平桌面上做匀速直线运动，水平拉力F₂的大小等于滑动摩擦力F_f的大小。滑动摩擦力F_f = μF_N，即F₂ = μF₁，因此μ =\(\frac{{{F_2}}}{{{F_1}}}\)

 

11．用如图（a）、（b）所示的两种方式都可以将一桶水提起来，可判断图（a）中桶受到的两个拉力F₁、F₂为共点力，理由是______________________，F₁、F₂与图（b）中桶受到的一个拉力F的效果相同，F可视为F₁、F₂的______力，F₁、F₂可视为F的_____力。

【答案】

F₁、F₂的作用线相交，合，分

 

12．大小为10 N和5 N的两个共点力的合力大小的范围为_______。

【答案】

 5～15 N。提示：两力的夹角为0°时合力最大，夹角为180°时合力最小。

 

13．大小分别为3 N、4 N、5 N的三个共点力的合力最大为_______N，最小为____N。

【答案】

12，0。提示：三个力方向相同时，合力最大；若3 N、4 N、5 N可以构成三角形，则三个力的合力为0。

 

14．两个大小均为F，互相垂直的共点力的作用效果是否能用一个大小也为F的力来替代？说明理由。

【答案】

不能。以大小相等相互垂直的力F为邻边所做的平行四边形为正方形，对角线长为\(\sqrt 2 \)F，即这两个力只可用一个大小为为\(\sqrt 2 \)F的力来替代。

 

15．如图所示，在同一平面内的三个共点力F₁、F₂、F₃，其大小均为50 N，相互间的夹角均为120°，其合力为_______N；若F₁、F₂的方向不变，将F₃在同一平面内转动60°，则这三个力的合力大小为______N。

【答案】

0，50。提示：因原本的三个力合力为零，将F₃转过60°后三个力的合力，可等效为求一个与原F₃方向相反、大小相等的力Fʹ₃和一个与原F₃大小相等、夹角为60°的力Fʺ₃（Fʹ₃与Fʺ₃的夹角为120°）的合力。

 

16．在“探究两个互成角度的力的合成规律”的实验中，下列操作是否正确或必要？若无必要或错误，说明理由。

操作	判断	说明理由或举例
将橡皮筋的一端固定，另一端套上两个绳套
将两个弹簧测力计分别钩住绳套，互成角度地将橡皮筋拉长至某一位置
记下橡皮筋的原长和伸长的长度
记下绳套结点的位置，在读取弹簧测力计的示数时，手应按住结点不动
记下拉力（即绳套）的方向
用一个弹簧测力计代替两个弹簧测力计将绳套的结点拉到同一位置，读取弹簧测力计的示数，记下拉力的方向
利用平行四边形定则画两个弹簧测力计拉力的合力，通过修改使画出的合力尽可能与一个弹簧测力计的拉力相符
改变拉力间的夹角再做几次实验

【答案】

对，符合实验操作要求；

对，符合实验操作要求；

不必要，因橡皮筋一端已固定，只需记录另一端的位置就能反映橡皮筋的形变情况，无需记录长度；

错，用手按住结点会影响弹簧测力计的读数；

对，绳套的方向即为拉力的方向；

对，结点拉到同一位置，说明两次拉橡皮筋的作用效果相同；

错，应以两个弹簧测力计的拉力为邻边画平行四边形，将其对角线与一个弹簧测力计的拉力进行比较，以此探究共点力合成的规律，而不是修改实验中记录的数据；

对，符合实验操作要求

 

17．两个共点力F₁、F₂的大小不同，通过分析或举例说明它们的合力F的大小是否符合下表中给出的说法。

说法	分析或举例
F1增加10 N，F2减少10 N，F的大小可能不变
F1、F2同时增加10 N，F一定增加20 N
F1、F2同时增大一倍，F一定增大一倍

【答案】

若F₁和F₂方向相同，则该说法成立；

若F₁和F₂方向相反，则该说法不成立；

根据平行四边形定则作图，无论F₁和F₂的夹角如何，该说法一定成立。

 

18．已知三个共点力的大小分别为F₁ = 50 N，F₂ = 40 N，F₃ =30 N，方向如图所示，F₁与F₂的夹角为37°，F₂与F₃垂直，则这三个力的合力的大小为________N，方向________。

【答案】

80，与F₂相同。提示：F₁与F₃的合力和F₂大小相等、方向相同。

 

19．我们常说：在困难面前，人多力量大，只要人人出力，形成合力，一定能够克服困难。从物理学的角度判断这句话是否合理。

【答案】

只要人人出力均会形成合力，但合力不一定大。因为力的合成遵循平行四边形定则，不是简单的数值相加。假使每个人出的力大小不变，如果各个力间的夹角改变，合力也会改变。例如，三个力大小相等，任意两个力的夹角互成120°时，它们的合力为0。当然，如果大家向同一方向出力，合力就大了。

 

20．在“位移、路程、速度、力、质量”五个物理量中，属于矢量的是__________。矢量的合成和分解都遵循_____________定则。

【答案】

位移、速度和力，平行四边形

 

21．如图所示，绳子对轮胎的拉力可以沿_______和_______两个方向进行分解。

【答案】

水平，竖直

 

22．判断下列关于力的分解的说法是否正确，说明理由。

说法	判断	分析或举例
一个力只能分解为两个分力
分力的大小可能大于被分解的力
可以按力的作用效果来确定分力的方向
一个力分解为两个共点力的结果是唯一的
一个力分解为两个大小相等的力，两个分力与合力的夹角一定相等

【答案】

错，只要合力和所有分力的作用效果相同，一个力可被分解为任意多个力；

对，合力大小不仅和两个分力大小有关，还取决于两个分力之间的夹角。考虑一个特例：两个分力大小相等，当两个分力之间夹角小于120°时，合力大于分力，反之则小于分力；

对，这是力分解的常用方法之一；

错，一个力分解为两个共点力有无数种可能；

对，两个大小相等的分力构成的平行四边形为菱形，合力位于对角线上，与两个分力间的夹角相等

 

23．在某确定平面内，共点力F₁与F₂的合力为F，F的大小为50 N，方向确定。分力F₂的大小为30 N，分力F₁的方向与合力F的方向成30°。某同学认为根据上述信息即可确定F₂的方向及F₁的大小和方向。你是否认同他的观点？说明理由。

【答案】

根据上述信息可以确定F₂的方向和F₁的大小和方向，结果如图所示，F₁可能沿两个不同的方向，在每个方向上其大小均有两种可能。所以，F₂有①②③④四个不同的方向。

 

24．明朝谢肇淛《五杂俎》中记载：“姑苏虎丘寺庙倾倒，议欲正之，非万缗不可。一游僧见之，曰：无烦也，我能正之。”游僧每日将木楔从塔身一侧的砖缝间敲进去，经月余扶正了塔身。游僧所为可用图简化表示，将夹角为θ的直角三角形斜劈卡在塔身上的缝隙中扶正塔身。水平方向的力F作用在斜劈上。

（1）求水平力F垂直于斜劈上、下表面的分力。

（2）分析与讨论实际情况下，斜劈的受力情况。

【答案】

（1）\(\frac{F}{{\cos \theta }}\)，Ftanθ

（2）水平力F可等效为两个垂直于斜劈上、下表面的分力，如果θ接近90°，两个分力的大小远大于F，可将塔身顶起少许。在实际情况中，斜劈将受到重力、水平推力、塔垂直于其上、下表面的压力和塔平行于其上、下表面的摩擦力。

 

25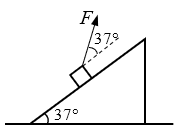．如图所示，物体放在倾角为37°的光滑斜面上，在方向与斜面夹角为37°的斜向上拉力F作用下，物体恰能保持静止。求拉力F沿斜面方向和垂直于斜面方向的分力，这两个分力的作用效果分别是什么？

【答案】

垂直于斜面向上的分力大小为0.6F，作用效果为减小物体与斜面间的挤压；沿斜面向上的分力大小为0.8F，作用效果为阻止物体沿斜面向下的运动。

 

26．如图所示，将一条钢丝固定在两栋相距80 m的高楼之间。杂技演员在钢丝中点静止时，凹陷的钢丝两边与水平方向之间的夹角均为10°，此时演员对钢丝中点竖直向下的作用力F的大小为500 N，则演员对钢丝的作用力沿着钢丝方向的两个分力的大小分别为多少？

【答案】

人对钢丝的压力有使钢丝伸长的效果，两个分力沿着钢丝伸长的方向，如图所示，大小为1 410.9 N。

 

27．如果站在电梯里的人处于平衡状态，则人保持__________或____________状态。

【答案】

静止，匀速直线运动

 

28．物体在三个以上共点力的作用下处于平衡状态，其中的一个力必定与其他几个力的合力大小_________，方向________。

【答案】

相等，相反

 

29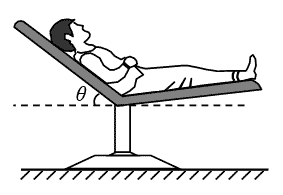．如图所示，某人躺在椅子上，椅子的靠背与水平面之间的倾角为θ。若此人所受重力为G，椅子各部分对他的作用力的合力大小为多少？

【答案】

椅子作用于人的合力的大小与重力大小相等

 

30．重为G的球，置于倾角为α的光滑斜面上，下方用垂直斜面的挡板挡住使球静止，受力分析如图所示。

（1）求斜面对球的支持力F_N1和挡板对球的支持力F_N2。

（2）若挡板竖直放置，斜面对球的支持力和挡板对球的支持力分别为多少？

【答案】

（1）Gcosα，Gsinα

（2）\(\frac{G}{{\cos \alpha }}\)，Gtanα

 

31．如图所示，用两根等长轻绳将木板悬挂在竖直木桩等高的A、B两点处，制成简易秋千。某次维修时两轻绳均被剪去一小段，但仍保持等长且悬挂点A、B的位置不变。木板静止时，F₁表示木板所受合力的大小，F₂表示单根轻绳对木板拉力的大小，则维修后F₁和F₂的大小发生了怎样的变化？

【答案】

由于木板始终处于静止状态，因此前后两次合力F₁都是0，保持不变。绳子各剪去一段后长度变短，悬挂木板时与竖直方向夹角变大，F₂变大。

 

32．如图所示，用一个水平力F推放置在粗糙斜面上的物体A，使它静止在斜面上，此时物体A受到哪几个力的作用？说明理由。

【答案】

如果水平力F、斜面支持力、重力三个力的合力为零，物体可能受到重力、斜面支持力和推力三个力作用，静止在斜面上；如果水平力F偏大或偏小，物体还受到斜面对它的摩擦力。

 

33．如图所示，当长木板与水平地面间的夹角α逐渐增大时，即木板从水平位置开始缓慢向竖直位置转动的过程中，原来静止在长木板上的物块受到的支持力和摩擦力的大小如何变化？

【答案】

受到的支持力逐渐减小，α刚开始增大的阶段，物块受到静摩擦力的作用，静摩擦力F_f = mgsinα，其大小随α的增加而增大；当α达到某一值后，物块开始下滑，此后物块受到滑动摩擦力的作用，滑动摩擦力F_f = μmgcosα，其大小逐渐减小。

 

34．如图所示，光滑的四分之一圆弧轨道AB固定在竖直平面内，A端与水平面相切。穿在轨道上的小球在拉力F的作用下，缓慢地由A向B运动，F始终沿轨道的切线方向，轨道对球的弹力为F_N。在运动过程中F的大小和F_N的大小如何变化？

【答案】

F增大，F_N减小

提示：在运动过程中，G大小和方向始终不变，F_N与F始终互相垂直，可借助作图来分析。

 

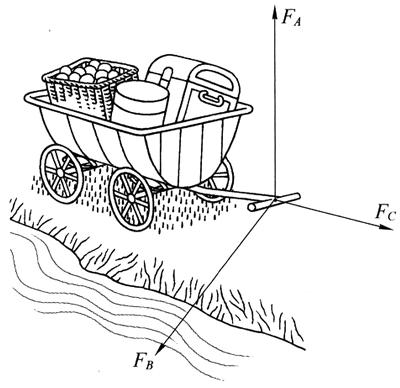
35．在《天鹅、梭子鱼和虾》的寓言中，三种动物同时拉车，天鹅用力F_A向上使劲拉，梭子鱼用力F_B向水里用力，大虾用力F_C沿着路面向前拉，如图3–17所示。三只动物齐心协力，车子却纹丝不动。为了拉动车子，三只动物应怎样调整用力方向？

【答案】

除了三个拉力，车子还受到摩擦力的影响，这四个力的合力的水平分力为零，所以车子不动，为了拉动车子，天鹅和梭子鱼通过改变用力方向，都可以减小与F_C的夹角，梭子鱼还可以同时减小与水平面的夹角。