1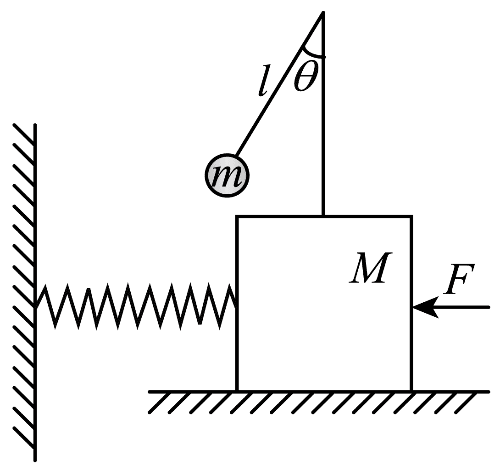．高层建筑（大楼）在风的作用下会发生晃动。在特定条件下，大楼的晃动幅度会变得较大，影响到安全 。

（1）为了减小晃动幅度，通常会在高层建筑上加装阻尼器，例如悬点固定在大楼上、摆锤质量为 m、摆臂长度为 l 的摆，摆臂是刚性的，质量可以忽略；大楼在风作用下的运动可简化为谐振子的强迫振动，谐振子的质量为 M，恢复力等效为劲度系数为 k 的弹簧，大楼在运动过程中可视为刚体。整个摆和谐振子系统如图所示，系统的总质量为 m 与 M 之和。风可视为水平方向上的强迫力 F（向左为正），它随时间 t 的变化为

F(t) = Hcosωt

其中振幅 H 和频率 ω 均为常量。重力加速度大小为 g。为简单起见，只考虑摆和谐振子的小幅度振动（因而摆便成为单摆）。

（1.1）求谐振子因强迫力 F 的作用产生的稳定振动的振幅；

（1.2）指出在没有阻尼器的情况下，风的频率为多大时，大楼受迫振动的振幅最大？对此频率的风，阻尼器应满足何种条件会最大限度地减小大楼的受迫振动？

（2）若风的频率为第（1.2）问中求出的风的频率的 \(\sqrt {0.99} \) 倍，在没有阻尼器的情况下，求此时大楼受迫振动的振幅有多大？若安装的阻尼器参数 l 符合第（1.2）问中得到的条件，为了使得大楼在此风的作用下的受迫振动的振幅减到无阻尼器时的 1 %，阻尼器的质量 m 应该为 M 的多少倍？

（3）实际的阻尼器还装有其他装置以提供阻尼力，通常做法是将摆锤浸泡在固定于建筑物上的油池中（相对于建筑物的质量，油的质量可以忽略；油池质量可视为已包含在大楼的质量之内）。已知当摆锤与油的相对速度为 vʹ 时，摆锤受到的阻尼力为

f = − γvʹ

其中 γ 为常量。试写出考虑加上阻尼力后系统的运动方程组（列方程组时不做小幅度近似，无需求解该方程组），为简单起见，假定摆球摆动时，油可视为相对于油池（固定在大楼上）静止。试根据你的理解定性分析为什么阻尼力是必不可少的。

【答案】

（1）（1.1）A = \(\frac{{(\omega _0^2 - {\omega ^2})H}}{{(\omega _0^2 - {\omega ^2})(k - M{\omega ^2}) - m\omega _0^2{\omega ^2}}}\)；（1.2）l = \(\frac{{Mg}}{k}\) 或 m 尽可能大

（2）\(\frac{1}{{100}}\)

（3）未整理
 

 

2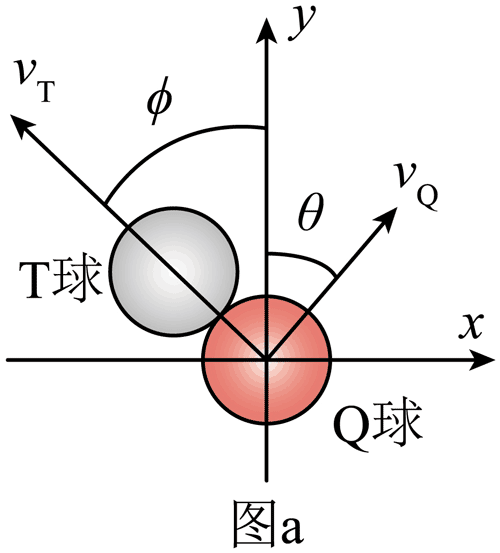．打台球时常用 Q 球撞击目标 T 球，如图所示。Q 球与 T 球的质量 m 和半径 R 均相同，且两球质量分布都是均匀的；Q 球在碰撞前的瞬间具有质心速度 v₀ 和转动角速度 ω₀，v₀ 沿 y 方向；碰撞时间极短，且 Q 球和 T 球之间没有摩擦，可认为两球碰撞是完全弹性的，球与桌面可视为点接触。

（1）在发生碰撞后的瞬间，T 球和 Q 球的飞行方向与 y 轴之间的夹角分别为 ϕ 和 θ（见图 a）。求碰撞后的瞬间，两球飞行方向之间的夹角的值以及 Q 球的质心速度 v_Q 和转动角速度 ω（用 ϕ，v₀，ω₀ 等表示）。

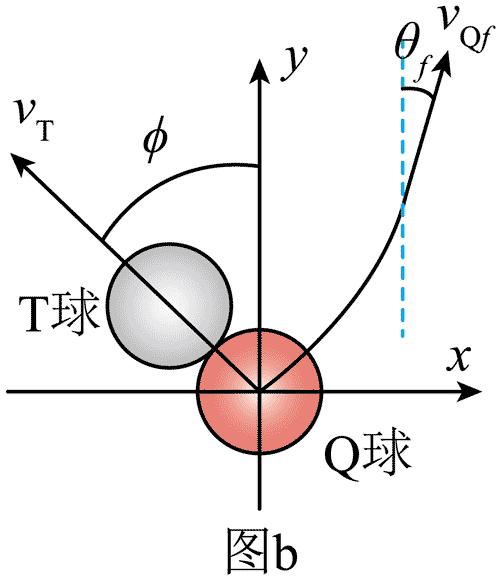（2）如图 b，Q 球碰撞后在摩擦力的作用下，需要经过 Δt 时间才能达到无滑滚动（也称纯滚）。已知 ϕ，v₀，ω₀ 和 Q 球与桌面之间的摩擦系数 μ。以下各小问的结果用，μ，m，R，ϕ，v₀，ω_0x，ω_0y 以及重力加速度 g 等表示。

（2.1）在碰撞后任意时刻，Q 球上与桌面的接触点称为此时刻的 C 点，在碰撞后的瞬间，求 C 点相对于桌面的速度 v_C0 的 x、y 分量的表达式；

（2.2）求碰撞后 Q 球达到纯滚所需时间 Δt；

（2.3）求在碰撞后直至纯滚前，Q 球质心运动的轨迹 x(t)，y(t)；

（2.4）Q 球达到纯滚后，定性指出 Q 球质心运动的轨迹形状，给出其质心的速度 v_Qf 与 y 方向之间的夹角 θ_f 的正切 tanθ_f 的表达式。

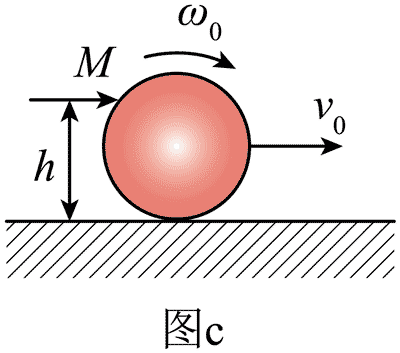（3）如图 c，台球手在开球时用球杆击打处于静止状态的 Q 球，在极短的时间内给球上某点赋予一个水平冲量 M，该点在竖直大球面高度 h 处，M 的方向在过该点的竖直大球面内，使得作用后小球获得质心速度 v₀（沿图 b 的 y 方向），以及转 动角速度 ω₀，当 h 取特定值时，可使得 Q 球无滑滚动飞向 T 球。求此特定值。

（4）现探讨台球手熟悉的 30° 角经验规则：自然伸开食指和中指（两指间角度大致为 30°）；食指指向 Q 球初始飞行方向，在某些碰撞条件下，中指将大致告知球手 Q 球最终的飞行方向。在第（3）问中的条件下，Q 球与 T 球发生弹性碰撞后，已知 T 球沿角度 ϕ 飞出（见图 a），求

（4.1）在碰撞后直至达到纯滚前的过程中，Q 球质心运动的轨迹 x(t)；y(t)；

（4.2）Q 球最终飞行方向与 y 轴之间的夹角 θ_f 的正切 tanθ_f 的表达式；

（4.3）当 T 球的飞出角度 ϕ 取某角度 ϕ_m 时，θ_f 具有一个极大值 θ_fm，求 ϕ_m 和 θ_fm 的值，计算在 ϕ = ϕ_m ± 5° 和 ϕ_m ± 10° 时的 θ_f 并将求出的这 6 个值填入下表：

ϕ	ϕ =	ϕm + 5°	ϕm + 10°	ϕm − 5°	ϕm − 10°
θf

【答案】

略

 

3．液体与其它介质（包括其蒸汽）之间的分界面称为液体的表面，液体的表面有表面张力，液体的表面张力系数是表征其性质的重要特征量之一。

（1）某油井内未抽出的石油（油气混合物）的温度为 100 ℃，它的密度是混有表面活性物质的水（简称“水”）的 80 %，比热容量是“水”的 60 %，记此石油的状态为参考状态。这种石油和“水”的混合物的表面张力系数 σ 与其温度 T（单位 K）和压强 p（单位 bar）的关系可以近似表述为

σ /(10⁻³ N/m) = 60 + 0.065T /K – 24.0p /bar + 3.15p² /bar²

该混合物的等体压强系数（系统在体积不变情况下其温度升高 1 K 所引起的系统压强的变化）为 β = 7.28×10⁻³ bar/K。参考状态下混合物的压强和温度之间成正比，比例系数也为 β。岩层某一特定区域充满处于参考状态的石油，现抽出其一半，在抽出石油的过程中同时注入等体积的“水”，以使此区域的石油和“水”的混合物的总体积始终保持不变，即等于刚开始抽取石油时的此岩层区域石油所占的体积，且假设未被抽出的一半石油与注入的“水”能均匀混合，混合过程中，混合物的体积始终等于被混合的石油和“水”的体积之和；由于抽出石油的过程较快，被抽出的石油与注入的“水”之间的热量交换可以忽略。试通过具体计算说明，为保证该油井高产，即使此区域的石油和“水”的混合物达到表面张力系数最小，注入的“水”的温度应为多少摄氏度。

（2）假设液体表面张力的存在，可以全部归结为表面层内和液体内部的每个粒子邻近粒子数目的不同，且液体表面层内的粒子间距与液体内部的粒子间距相同。设液体表面层内每个粒子邻近粒子数目是液体内部每个粒子邻近粒子数目的 ζ 倍（0 < ζ < 1），记液体的摩尔质量为 μ，摩尔汽化热为 L_m，质量密度为 ρ，阿伏伽德罗常量为 N_A，试导出该液体的表面张力系数 σ 的表达式。

【答案】

（1）35 ℃

（2）σ = (1 − ζ)\(\frac{{{L_{\rm{m}}}}}{{{N_{\rm{A}}}}}{\left( {\frac{{\rho {N_{\rm{A}}}}}{\mu }} \right)^{2/3}}\)

 

4．（1）质子、中子等是实验上可观测的微观粒子，为研究微观粒子的性质和结构，从而探索物质及其质量的起源，人们花费大量的财力物力建造高能粒子加速器。质子半径大约 0.850 fm，并由带电荷和不带电荷的粒子组成。为研究质子内部的电荷分布，人们希望利用电子对它进行 200 层的断层扫描，试确定所用的被加速的电子的动能（以 GeV 为单位）为多大？并通过计算回答：狭义相对论和极端相对论的结果之间的差别是否小于与狭义相对论结果的 1 %？第（1）问中不计电磁相互作用的影响。

（2）静止质量为 m、带电量为 Z₁e 的粒子与带电量为 Z₂e 的固定靶之间发生散射。求：当二者中心间距为 r，带电量为 Z₁e 的粒子的动量大小为 p 时此系统的总能量。对于入射粒子 A 和固定靶 B 均为质子的情况，且当 A、B 两质子的中心之间的距离测量的不确定度等于它们中心的间距时，试确定入射质子 A 的速率 v 的值。假设这里的两个质子中心之间的间距测量的不确定度与粒子 A 位置测量的不确定度近似相等。第（2）问限于非相对论情形。

已知电子电量大小为 e = 1.60×10⁻¹⁹ C，电子质量为 m_e = 9.11×10⁻³¹ kg，普朗克常量为 h = 6.63×10⁻³⁴ kg·m²/s，真空中的光速为 c = 3.00×10⁸ m/s，真空介电常量 ε₀ = 8.85×10⁻¹² C²/(N·m²)。

【答案】

（1）是

（2）0.015c

 

5．2001 年诺贝尔物理学奖授予埃里克·康奈尔、沃尔夫冈·克特勒，以及卡尔·韦曼。三位科学家的获奖理由是实现了碱金属原子气体中的玻色–爱因斯坦凝聚态。为此，他们采用了磁阱囚禁和蒸发冷却两项关键技术。

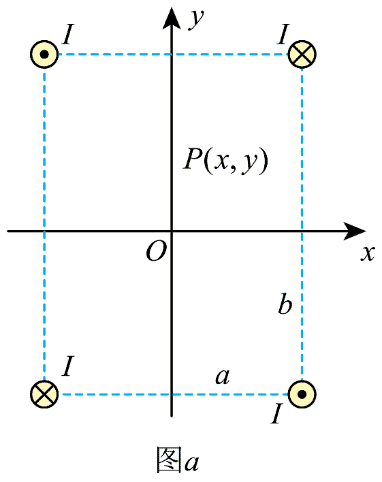
（1）利用磁阱囚禁原子的一种常见装置是所谓 Ioffe 势阱。Ioffe 势阱由四根横截面积可忽略、相互平行的无限长直导线组成。这四根导线垂直穿过一边长为 a 和 b 的长方形的四个顶点。导线中通以大小相同的电流 I，电流方向如图 a 所示。以长方形中心 O 点为原点，垂直于长度分别为 b、a 的边的直线为 x，y 轴，建立右手直角坐标系，任取 x – y 平面上原点附近一点 P，其坐标为（x,y,0）（x ≪ a，y ≪ b，a 和 b 为同阶量），求 O、P 两点的磁感应强度；所得结果如果可做小量近似的，试将所得结果做小量近似并保留至领头阶。

（2）一个固有磁矩为 S 的原子会受到磁场的作用。假设原子的磁矩可视为由形状和电流在其旋转过程中均保持不变的微小电流圈所提供，证明其在磁场 B 处中的势能为 W_m = − S·B。

（3）将第（2）问中的原子囚禁于 x – y 平面上原点附近的任一点 P 点，并通过实验手段调控使该原子的磁矩方向始终与 P 点磁场方向相反，求其所受的磁场力，结果保留至领头阶。

（4）实现玻色–爱因斯坦凝聚态的另一个重要条件是降温，也就是将原子气体的平均能量降低。常用的一种方法称为蒸发冷却，其原理是将具有高能量的原子蒸发掉，从而降低剩下原子的平均能量。设有一团原子气体，通过实验手段调控每个原子的磁矩方向始终与它所处位置的磁场方向相反，进而被上述 Ioffe 势阱囚禁在一高度固定的圆柱形区域内，圆柱体的横截面为平行于 x – y 平面、半径为（R₁ ≪ a,b，柱体高度远小于 R₁）的圆，被囚禁的原子的密度近似均匀。以 O 点为势能零点，求这团原子气体在外磁场中的平均势能。如果缓慢地将一部分原子蒸发掉，使得剩余原子冷却且向中心收缩为半径为 \(\frac{{{R_1}}}{5}\)、高度不变的圆柱形区域，原子密度保持不变，求冷却后原子团的总原子数、原子团在外磁场中的总势能和原子平均势能。已知真空磁导率为 μ₀。

【答案】

略

 

6．爱因斯坦的广义相对论预言星光会在太阳附近发生偏折。1919 年，英国天文学家埃丁顿率领一支队伍，藉发生日全食的机会对这个现象进行了观测，验证了上述预言。下面对此进行分析。

（1）先在牛顿的动力学和万有引力理论的框架下考虑。若质量为 m 的质点在位于坐标原点 O 的质量 M（M ≫ m）的引力场中运动，其轨道是圆锥曲线。在平面极坐标系（r,θ）中，轨道方程为 r（θ）= \(\frac{p}{{1 + e\cos \theta }}\)（− π < θ ≤ π），p（p > 0）称为半通径，e（e ≥ 0）称为偏心率。若 e > 1，则存在 θ_max，使 − θ_max < θ < θ_max，试确定 θ_max 及其取值范围。

（2）第（1）问中的质点的轨道的参数 p 和 e 由质点的能量 E（含动能和相互作用势能）和相对于 O 点的轨道角动量的大小 L 决定。试导出 p = p（E,L）和 e = e（E,L）的函数关系。

（3）设一物体以速度 v₀ 从外太空飞入太阳系，朝向太阳的瞄准距离是 b（即初速度 v₀ 所在直线到太阳中心的距离），如图所示。设 \(\frac{{v_0^2b}}{{G{M_ \odot }}}\) ≫ 1，其中 M_⊙ 是太阳质量。当它飞离太阳系时，对下述两种情况，求其飞出方向相对于原飞入方向的偏转角 Δφ；

（ⅰ）该入射物是一块陨石；

（ⅱ）该入射物是一束星光，且该光束恰好掠过太阳表面而射入到我们的观测站，此时可近似认为瞄准距离 b 等于太阳半径 R_⊙。

（4）广义相对论断言星光在引力场中会弯曲，在弱场近似下，这等效于存在引力场的空间有不恒为 1 的相对折射率

\[{n_{{\rm{eff}}}}(r) = 1 - \frac{{2\varphi (r)}}{{{c^2}}}\]

其中 φ（r） 是空间中的质量分布在 r 处的牛顿引力势。光线的轨迹可由费马原理 δ \(\int_{\rm{A}}^{\rm{B}} {{n_{{\rm{eff}}}}(r){\rm{d}}l} \) = 0 决定，其中 \(\int_{\rm{A}}^{\rm{B}} {{n_{{\rm{eff}}}}(r){\rm{d}}l} \) 是 A 到 B 的光程，变分符号 δ 表示总光程取极小值。设 n_eff 与 θ 无关，即 n_eff = n_eff（r），若光线的轨迹方程为 θ = θ（r），上述变分就导致方程 \(\frac{{\rm{d}}}{{{\rm{d}}r}}\left( {\frac{{{r^2}\theta '}}{{\sqrt {1 + {r^2}\theta '} }}{n_{{\rm{eff}}}}(r)} \right)\) = 0，这里 θʹ ≡ \(\frac{{{\rm{d}}\theta }}{{{\rm{d}}r}}\)。利用此方程，试重新计算掠过太阳表面的星光的偏折角。

已知太阳的质量为 M_⊙，太阳半径为 R_⊙。引力常量为 G，真空中的光速为 c。

【答案】

（1）\(\frac{\pi }{2}\) < θ_max < π

（2）e = \(\sqrt {1 + \frac{{2E{L^2}}}{{{G^2}{M^2}{m^3}}}} \)

（3）（ⅰ）Δφ = \(\frac{{2G{M_ \odot }}}{{v_0^2b}}\)；（ⅱ）Δφ = \(\frac{{2G{M_ \odot }}}{{{c^2}{R_ \odot }}}\)

（4）Δφ = \(\frac{{4G{M_ \odot }}}{{{c^2}{R_ \odot }}}\)

 

7．上世纪六十年代初，人们在实验上发现了超导环内的磁通量的量子化现象。磁通量子的单元是 \(\frac{h}{{2e}}\)，其中 h = 2πℏ 为普朗克常量（ℏ 为约化普朗克常量），c 为真空中的光速，− e 为电子电量。为了理解这一现象，考虑一维圆环上非相对论无相互作用电子的稳定运动状态，如图 a 所示。已知电子质量为 m，环的半径为 R，环上电子的运动状态可以用以下波函数表示，

Ψ（x）= exp（\(\frac{i}{h}\)px）

其中，x = Rθ 标记以圆环中心为原点的极坐标系统（ρ,θ）中环上的位置，p 是电子的动量。

（1）一维的圆环上电子的波函数 Ψ（x）应当满足单值性条件，试据此给出电子动量 p 所有可能的取值。

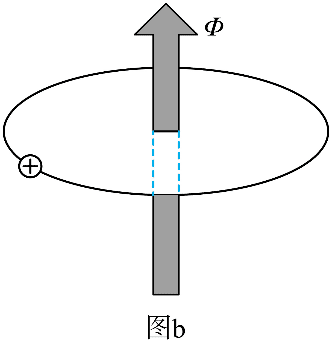（2）在环中通入磁通 Φ（Φ 关于过圆心且垂直于圆面的轴对称，图中箭头表示磁通的正负。在本题的计算中，Φ 视为连续变量），如图 b 所示。此时电子的动量变为

pʹ = p + eA

其中 A 为电磁场的矢势，其方向可视为沿环的切线方向。电子的能量由 E = \(\frac{{{{p'}^2}}}{{2m}}\) 给出。试据此给出此时单个电子的能量 E 与磁通量 Φ 的关系。

（3）考虑环上 N 个无相互作用的电子构成的系统。在接近绝对零度时，由于量子效应，系统满足以下两个条件：

（3.1）任意两个电子具有不同的动量

（3.2）系统总能量取最小值

证明该系统的总能量 E_tot 随磁通量 Φ 周期性变化，并指出该周期的大小。

（4）在 − \(\frac{h}{{2e}}\) ≤ Φ ≤ \(\frac{h}{{2e}}\) 的范围内，试给出系统单粒子平均能量 \(\bar E\)  = \(\frac{{{E_{{\rm{tot}}}}}}{N}\) 随 Φ 的变化关系；并由此指出，当 N 为奇数时，Φ = 0 时的平均能量小于 |Φ| = \(\frac{h}{{2e}}\) 时的平均能量；当 N 为偶数时，Φ = 0 时的平均能量大于 |Φ| = \(\frac{h}{{2e}}\) 时的平均能量。

（5）在超导体中，电子之间存在一种配对机制：为了使电子的平均能量最低，动量为 pʹ 和− pʹ 的电子要么同时存在，要么同时不存在。考虑总电子数是 2N 的两个环，且每个环上的电子数目不固定。即这 2N 个电子可以在两个圆环上任意分配。

（5.1）证明：若两个环分别带有奇数个电子，则当两环中的电子数相差最小且 Φ = 0 时，电子的平均能量才最低；类似地，若两个环分别带有偶数个电子，则当两环中的电子数相差最小且 Φ = \(\frac{h}{{2e}}\) 时，电子的平均能量才最低。记这两种电子平均能量最低的情形为 a 和 b，继而证明：无论是 a 还是 b，动量为 pʹ 和− pʹ 的电子要么同时存在，要么同时不存在。

（5.2）证明在以下两种（a 和 b）双环体系中，电子的平均能量的比值在环中的电子数趋于无穷大时趋于 1：a．两环各自带有的电子数均为 N = 2M + 1 且 Φ = 0；b．两环分别带相差为 2 的偶数个电子，即两环带有的电子数分别为 N₁ = 2(M + 1) 和 N₂ = 2M 且 Φ = \(\frac{h}{{2e}}\)。其中 M 为正整数。

【答案】

（1）p = n\(\frac{\hbar }{R}\)，n = 0，±1，±2……

（2）E_n = \(\frac{{{\hbar ^2}}}{{2m{R^2}}}{\left( {n + \frac{{e\Phi }}{h}} \right)^2}\)，n = 0，±1，±2……

（3）见解析，\(\frac{h}{{e}}\)

（4）\(\frac{{{\hbar ^2}}}{{2m{R^2}}}{\left( {\frac{1}{2} + \frac{{e\Phi }}{h}} \right)^2} + \frac{{{\hbar ^2}}}{{2m{R^2}}}\left( {\frac{{{M^2}}}{3} - \frac{1}{{12}}} \right)\)，当 N 为奇数时，Φ = 0 时的平均能量小于 |Φ| = 时的平均能量；由⑯⑱式可见，当 N 为偶数时，Φ = 0 时的平均能量大于 |Φ| = 时的平均能量

（5）略