1．自然界中有各种运动形式，机械运动是其中的一种。做机械运动的物体，其______随______发生变化。

【答案】

空间位置，时间

 

2．质点是物理学中的一个理想模型。将所研究的物体视为质点的条件是：______________________________________________________________________，例如：________________________________________________________________________。

【答案】

物体的大小和形状对研究的问题可以忽略，研究从上海驶往北京的列车通过的路程时，可将列车视为质点

 

3．物理学在研究物理现象时，总是要把实际研究对象简化、抽象为________，这样做的意义在于_______________________________________________________________。

【答案】

物理模型，突出影响研究的主要因素，忽略次要因素

 

4．在研究下列问题时，可将研究对象视为质点的是（    ）。

A．沿斜槽下滑的小钢球的转动快慢

B．人造卫星绕地球运动的周期

C．木箱在水平力作用下是否会在水平面上翻滚

D．船舶远洋航行的速度

【答案】

BD

 

5．如图所示，2009年7月22日发生的日全食是一次日全食天文奇观。某同学认为在分析日全食的成因时不能将月球视为质点，你是否认同他的观点？说明理由。

【答案】

认同，日全食发生是因为日、月、地排列在一条直线上，月球刚好遮挡了太阳，这时不能忽略月球的大小和形状，不能将月球视为质点。

 

6．判断以下关于质点的说法是否正确，说明理由。

说法	判断	说明理由或举例
只要物体的体积很小，就可以视为质点
只要物体沿直线运动，就可以视为质点
抽象为质点后，物体的大小和质量均可忽略不计
某些条件下，地球可被视为质点

【答案】

错，如果关注物体上各点运动的差异，或者该物体的运动距离与其大小可相比拟，就不能视为质点。

错，物体做直线运动并不一定可以视为质点，如教材节首图所示的情景，研究列车通过隧道的时间，如果列车和隧道的长度可比拟，就不能将列车视为质点

错，物体视为质点后，其大小和形状可以忽略，但质量不能忽略

对，虽然地球相对人体而言很大，但是研究地球绕太阳的公转时，还是可以忽略地球的大小和地球上各点的运动差异，将地球视为质点

 

7．为研究运动员沿着平直跑道跑动的快慢，某同学猜想身体某一部位的运动可以近似视为直线运动，用这个部位的运动来代表运动员整体的运动。为了验证这种猜想，他设计了一个方案：在操场直跑道上每隔1 m做一个明显的记号，在一位同学的肩、腰、臀、肘、膝贴上不同颜色的圆形标记，拍摄一段同学沿直跑道跑动10 m的视频。你能根据视频绘制各个标记点的轨迹，由轨迹解释哪个标记点最能代表运动员整体的运动吗？

【答案】

拍摄视频时，设备需保持静止。利用信息技术，将视频处理成与教材“问题与思考”第2题相似的照片。将照片中同学身上的相同颜色的标记点连线，获得各色标记点的不同轨迹，找出其中最接近直线的一条。本题所需的视频可根据情况由学生自主拍摄或由教师提供。本题呈现了提出猜想、收集证据、作出解释的科学探究的一般过程，与教材“问题与思考”第2题呼应

 

8．某人从入口A进入公园，一路游览到景点B。如果知道此人运动的位移，则______知道A、B两点间的直线距离，______知道此人运动的路径。（均选填“可以”或“不可以”）

【答案】

可以，不可以

 

9．描述列车从上海驶向北京的运动，时刻与列车运动过程中的______相对应，时间与列车运动过程中的______相对应。（均选填“位置”或“位移”）

【答案】

位置，位移

 

10．可用文字叙述、________和________三种方式描述物体的运动。

【答案】

数学关系，图像

 

11．下列说法中，哪些指的是时刻，哪些指的是时间间隔？

（1）篮球比赛规定，拥有球权的队必须在获得球后的24 s内投篮。         （    ）

（2）比赛还剩最后2 min。                                                                      （    ）

（3）商场上午10：00开始营业。                                                            （    ）

（4）这张照片的曝光时间是\(\frac{1}{{500}}\) s。                                                         （    ）

【答案】

（1）时间间隔 （2）时间间隔  （3）时刻     （4）时间间隔

 

12．如图所示的时间轴上，0～3 s的线段表示前3 s的时间，4～5 s的线段表示___________，“3 s”这个点既可以表示__________，也可以表示_______________________。

【答案】

第5 s时间，第3 s末时刻，第4 s初时刻或前3 s末时刻。

 

13．某车向东行驶了6 km，再向南行驶10 km，又向北行驶2 km。

（1）按比例画出该车运动路线的示意图，用字母标记各段运动的起止点。

（2）该车一共行驶了_______km的路程，该车的位移大小为_______km，方向为东偏南_______。

【答案】

（1）如图所示 

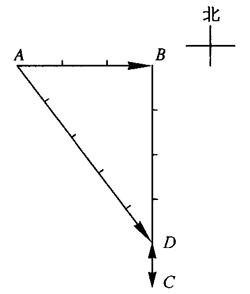
（2）18，10，53°

 

14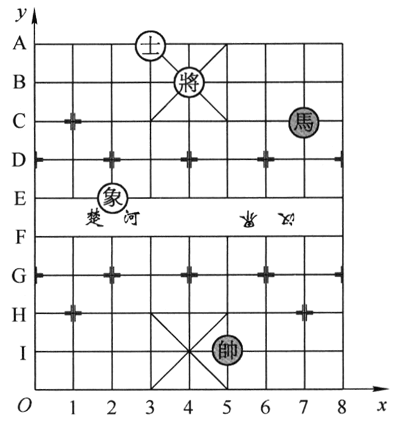．中国象棋棋盘上有10条横线，9条竖线。我们用如图1-4所示的平面直角坐标来描述棋子的位置，横轴上标数字，纵轴上标字母，棋子的位置可用“字母＋数字”的形式来描述。甲、乙双方对弈的过程中，甲方的“将”和乙方的“马”处于如图所示位置，乙方先走“马”，只需一步从C7到A6，即可形成对甲方的“将军”’之势。如果棋盘上的每一小格为边长3 cm的正方形，则这一步中，“马”的位移是多少？在图中画出其位移矢量。

【答案】

3\(\sqrt 5 \)cm，图略

 

15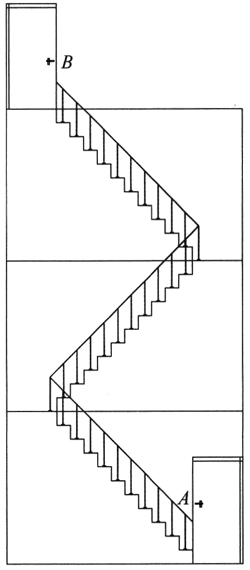．如图所示，塔楼的每层高度h均相同，楼梯的倾斜角度均为45°。某人从一楼的门A处走到四楼的门B处，其位移的大小和最小路程分别是多少？

【答案】

位移的大小是AB间连线的长度，为\(\sqrt 10 \)h，路程是三段楼梯长度之和，为3\(\sqrt 5 \)h

 

16．一只蚂蚁在地面上沿直线爬行，每隔10 s记录蚂蚁头部的位置，如图（a）所示。某同学认为蚂蚁的运动可以用图（b）中的位移-时间图像来描述。你是否认同该同学的观点？说明理由。

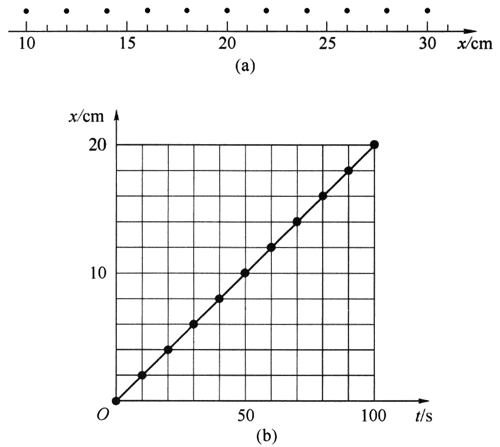
【答案】

认同，由图（a）可知，蚂蚁在100 s内匀速爬行了20 cm。图（b）中的直线同样描述了蚂蚁的运动情况，并且反映了其运动方向

 

17．在直线运动中，将物体在某段时间内的位移Δx与发生这段位移所用时间Δt的比称为平均速度。平均速度是矢量，其方向与_______方向相同，其大小表示这段时间内运动的___________。

【答案】

位移，平均快慢或大致快慢

 

18．平均速度对应___________的速度，瞬时速度对应__________的运动快慢。（均选填“某一段时间”或“某一时刻”）________速度可精确地描述变速运动的快慢和方向。高速公路限速标记表示______速度不得超过该数值。国产动车组“和谐号”试验时某时刻的车速高达486.1 km/h，指的是__________速度。（均选填“平均”或“瞬时”）

【答案】

某一段时间，某一时刻，瞬时，瞬时，瞬时

 

19．判断下列关于瞬时速度和平均速度的说法是否正确，说明理由。

说法	判断	说明理由或举例
汽车经过某直线路段的平均速度为5 m/s，表示该汽车在该路段上每秒的位移均为 5 m
汽车启动后第3 s末的平均速度是5 m/s
无限逼近某一位置附件的足够小位移对应的平均速度，可看作质点在这个位置的瞬时速度
短跑运动员以8 m/s的瞬时速度开始冲刺

【答案】

错，平均速度只能粗略描述某段运动的快慢，不能表示整段运动的细节。

错，第3 s 末是时刻，对应瞬时速度。

对，根据无限逼近思想，位移趋于0时，运动时间也趋于0，满足瞬时速度的定义。

对，8 m/s是冲刺阶段初始时刻的速度。

 

20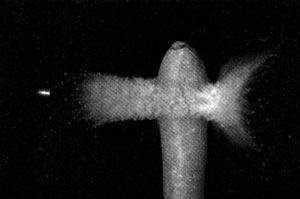．如图所示为高速摄影机拍摄的子弹射穿胡萝卜瞬时的图像。子弹的速度约为900 m/s，子弹长度为1.9 cm，估算子弹穿过胡萝卜所用的时间。

【答案】

9×10⁻⁵ s

【解析】

根据照片中胡萝卜直径和子弹长度10∶3的关系，先估算胡萝卜的直径d。把子弹看作质点：设子弹的速度在这么短的时间内不变，根据t = \(\frac{d}{v}\)就可估算出子弹穿过胡萝卜的时间为7×10⁻⁵ s。这样的估算比较粗糙，更接近实际情况的估算应考虑子弹的长度x，设子弹的速度在这么短时间内不变，根据t = \(\frac{{x + d}}{v}\)就可估算出子弹穿过胡萝卜的时间约为9×10⁻⁵ s。

 

21．一个做直线运动的物体，前一半位移的平均速度为v₁，后一半位移的平均速度为v₂，则全过程的平均速度为_________；另一个做直线运动的物体，前一半时间内的平均速度为v₁，后一半时间内的平均速度为v₂，则全过程的平均速度为_________。

【答案】

\(\frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}\)，\(\frac{{{v_1} + {v_2}}}{2}\)

 

22．滑块在水平气垫导轨上做匀速直线运动的x-t图像如图所示，判断下列说法是否正确，说明理由。

说法	判断	说明理由或举例
由图可知，滑块沿着PQ方向做匀速直线运动
根据图像，已知滑块的位置可求对应的时刻，已知时刻也可求得此时滑块所在位置
直线PQ的斜率越大表示滑块运动得越快
量出图中直线PQ的倾角α，tanα的值即为滑块做匀速直线运动速度的大小

【答案】

错，滑块做直线运动，但PQ不是滑块运动的轨迹。

对，x–t图反映了位移随时间变化的函数关系，自变量与因变量一一对应

对，按定义，x–t图像的斜率即为物体的运动速度

错。数学上倾角的正切值是在横轴和纵轴的分度相同时得出的，当图中横轴和纵轴所取的分度不同时，不能用量出的角度的正切值表示速度的实际大小。

 

23．如图所示为公路上的指示牌，圆牌上的数字为100，方牌上标有“前方区间测速，长度66 km”。

（1）根据上述信息，说明为何理论上驾驶员驾驶车辆通过该路段的最短时间为39.6 min。

（2）某辆车通过该路段的时间为45 min，却被交警判为超速。说明交警的判定依据。

【答案】

（1）圆牌表示该路段限速100 km/h，即车辆在这一路段任意位置的瞬时速度都不能超过该数值。该区间的长度为66 km，设车辆以100 km/h 的最高限速匀速经过该路段，将车辆视为质点，在不超速的前提下，最短用时为39.6 min。

（2）该车用时45 min，其平均速度未超过限制值。但在区间测速的路段中也设置了速度监测设备，该车在实际行驶过程中并非匀速行驶，其驶过监测设备时的瞬时速度大于100 km/h，故被判定为超速。

 

24．表一和表二记录了运动员在某次百米跑过程中不同时刻与位置的对应关系。则：

表一

t/s	0.00	1.00	2.00	3.00	4.00	5.00	6.00	7.00	8.00	9.00	10.00
x/m	0.00	8.01	17.90	28.00	39.00	50.00	61.10	71.98	82.32	91.02	100.00

表二

t/s	9.00	9.10	9.20	9.30	9.40	9.50	9.60	9.70	9.80	9.90	10.00
x/m	91.02	91.94	92.85	93.74	94.62	95.47	96.21	97.10	98.00	99.10	100.00

（1）运动员百米跑的平均速度是多少？

（2）运动员最后1 s的平均速度是多少？

（3）若要知道运动员9 s时的瞬时速度，应选择哪组数据？说明理由。

【答案】

（1）10 m/s

（2）8.98 m/s

（3）选择9.00～9.10 s这0.1 s内的位置变化0.92 m来估算，得9 s时的瞬时速度为9.2 m/s。理由是，这0.1 s 的时间最短，最接近9.0 s时的瞬时速度。

 

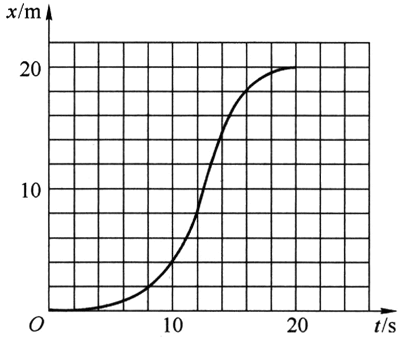
25．质点在0～20 s时间内的x-t图像如图所示，则质点在这段时间内的平均速度为______m/s，质点在这段时间内速度大小的变化情况为_____________（选填“变大”“变小”“先变大后变小”或“先变小后变大”）。在某一时刻t₀时，质点的瞬时速度等于从t = 0到t₀时间间隔内的平均速度，则t₀ = ________s。

【答案】

1，先变大后变小，16

【解析】

由图可知，x–t图像上各点切线的斜率先变大后变小，故瞬时速度的大小也随之相应变化。只有在t = 16 s时，该点的切线也是t = 0时刻与t = 16 s时刻两点的连线，该点符合题意。

 

26．一位乘客在 1 楼进入电梯。从l楼直达 8 楼用时 14 s。电梯在 8 楼停 10 s 后继续上升直达 15 楼，估算该电梯从 1 楼到 15 楼整个运动过程的平均速度。要估测电梯匀速上升时的速度，该如何测量？写出测量方案，说明需要测量的物理量和测量的方式。通过实际测量对自己的方案进行评价，提出改进的建议。实验时请同学们注意安全。

估算电梯的平均速度：

 

测量方案：

 

评价和建议：

 

【答案】

住宅楼的楼层高度约为 3 m，从 1 楼到 15 楼共上升了 42 m。1 楼到 8 楼上升了7层楼﹐用时 14 s，8 楼到 15 楼也上升 7 层楼，用时也是 14 s，在 8 楼停留 10 s，故从 1 楼到 15 楼共用时 38 s。由此可得，电梯的平均速度约为 1.1 m/s。

测量方案：站在楼边拍一张照片，根据身高与楼高的比例关系，估计楼层高度。拍摄一段电梯匀速上升阶段楼层提示数字跳动的视频，根据数字变化推断上升高度，根据进度条时问估计上升时间，两者结合估算电梯匀速上升的大致快慢。

 

27．速度和加速度都与“快慢”有关，速度是描述物体________快慢的物理量。加速度是描述物体________快慢的物理量。

【答案】

位置变化或运动，速度变化

 

28．速度和加速度都是利用比值法来定义的。我们把_______________的比称为速度，把_____________的比称为加速度。

【答案】

位移与所用时间，速度变化量与所用时间

 

29．速度和加速度都是矢量，加速度的方向总与________的方向相同。

【答案】

速度变化量

 

30．如果汽车行驶时的加速度为零，则该车的速度______，做________运动。如果汽车做加速直线运动，其加速度的方向与速度的方向________；汽车制动时，其加速度的方向与速度的方向_________。（后两空均选填“相同”或“相反”）

【答案】

不变，匀速直线，相同，相反

 

31．刚开始点火升空时，火箭的加速度可达14 m/s²，所以火箭的速度在1 s时间内增加了14 m/s。这一说法正确吗？为什么？

【答案】

不正确。题目中的14 m/s为瞬时加速度，在1 s内火箭的加速度并非始终为14 m/s²，因此1 s内速度不一定增加14 m/s。

 

32．一辆在公路上沿直线行驶的汽车，是否可能同时具有负的速度和正的加速度？如果可能，请举例说明；如果不可能，请说明理由。

【答案】

公路上，以观察者行驶的方向为正方向。反向车道正在制动减速的汽车就具有负的速度和正的加速度，速度与加速度的方向相反，说明运动物体的速度大小在减小。

 

33．某同学骑自行车从静止开始运动，经10 s后速度增大到5 m/s，在这段时间内自行车的速度变化量为_______m/s，平均加速度为_______m/s²；以5 m/s的速度到达路口附近后，自行车减速2 s即停止，在这段时间内，自行车的速度变化量为________m/s，平均加速度为_________m/s²。

【答案】

5，0.5，−5，−2.5

 

34．判断下列关于速度和加速度的说法是否正确，说明理由。

说法	判断	说明理由或举例
加速度大小不变，速度大小也一定不变
加速度越大，速度变化量也越大
加速度增大，速度也随之增大
加速度的大小减小时，速度的大小可能增大

【答案】

错，以匀加速直线运动为例，加速度大小不变，但速度大小变化。

错，速度变化量不仅与加速度有关，还与变化的时间有关。

错，加速度增大表示速度变化得更快，但是如果速度与加速度方向相反，速度会变小。

对，即使加速度大小在减小，只要加速度与速度方向相同，速度大小就会增大。

 

35．如图（a）、（b）所示分别为质点做直线运动的x-t图像和v-t图像，其中OBC和OBʹCʹ分别表示质点1和质点2的运动，DE和DʹEʹ分别表示质点3和质点4的运动。仿照下表第一行，将表格填写完整。

线段或点	表示的物理意义［图（a）］
OB	质点1速度不变
BC
DE
点F

 

线段或点	表示的物理意义［图（b）］
OBʹ	质点2以不变的加速度加速运动
BʹCʹ
DʹEʹ
点Fʹ

【答案】

质点1静止

质点3速度不变

质点1、3在某一时刻位于同一位置（相遇）

 

质点2速度不变

质点4以不变的加速度加速运动

质点2、4在某一时刻速度相同

 

36．车辆仪表盘上的速度计可以实时显示瞬时速度的大小。有同学认为，车辆在加速启动阶段和减速制动阶段的加速度大小都是恒定不变的。你是否认同他的观点？利用车辆速度计提供的信息及加速度的定义设计一个方案验证你的观点。

【答案】

拍摄汽车加速和制动阶段仪表盘的视频，通过进度条读取时间。用表格记录不同时刻仪表盘显示的速度，作出v–t图像。通过图像观察汽车的加速度是否恒定。