1．通常分子直径的数量级为________m；乒乓球直径是3.8 cm，其数量级为_______m；地球直径是12740 km，其数量级为_______m。

【答案】

10^-10，10^-2，10⁷

 

2．7℃相当于热力学温度_______K，如果温度降低1℃，则热力学温度降低了______K。

【答案】

280，1

 

3．太阳能是最清洁的新能源。为了环境保护，我们要大力开发像太阳能这样的新能源而减少使用像煤炭这样的常规能源，请划分下列能源的类别，把编号填入相应的表格：

①风能②核能③石油④潮汐能⑤地热能⑥天然气

类型	编号
常规能源
新能源

【答案】

③⑥，①②④⑤

 

4．如图所示，水平放置的一根玻璃管和几个竖直放置的U形管内都有一段水银柱，封闭端里有一定质量的气体，图（a）中的水银柱长度和图（b）、（c）、（d）中U形管两臂内水银柱高度差均为h＝10 cm，外界大气压强p₀相当于76cm水银柱产生的压强。则4部分密封气体的压强分别为：p_a＝____Pa；p_b＝____Pa；p_c＝____Pa；p_d＝____Pa。（水银密度ρ＝13.6×10³ kg/m³，重力加速度g取9.8 m/s²）

【答案】

1.01×10⁵，1.15×10⁵，8.80×10⁴，1.15×10⁵

 

5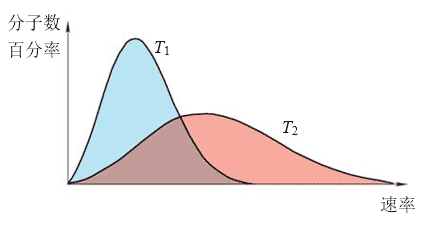．如图所示，横坐标表示分子速率，纵坐标表示各等间隔速率区间的分子数占总分子数的百分比。由此可以判断T₁_________T₂。（选填“大于”、“小于”或“等于”）

【答案】

小于

 

6．当热水瓶中的热水未灌满而盖紧瓶塞，并密封很好，那么经过一段时间后，要将瓶塞拔出来会很费劲，这是因为_____________________________________________________。现假设瓶内初温t₁＝87℃，经过一段时间降为t₂＝42℃，热水瓶口的横截面积S＝10 cm²，请估算，要拔出瓶塞至少需要_______N向上的拉力。（设大气压强p₀＝1.0×10⁵ Pa，不计瓶塞重力）

【答案】

封闭气体由于温度降低而体积不变，压强减小了；12.5

【解析】

（2）对瓶内气体，由查理定律可得：

\(\frac{{{p_1}}}{{{T_1}}}\)＝\(\frac{{{p_2}}}{{{T_2}}}\)

\(\frac{{1.0 \times {{10}^5}}}{{360}}\)＝\(\frac{{{p_2}}}{315}\)

p₂＝0.875×10⁵ Pa

对瓶塞进行受力分析，有：

F＋p₂S＝p₀S

F＝(p₀－p₂)S＝(1.0－0.875)×10⁵×10×10^-4＝12.5 N

 

7．布朗运动是说明分子运动的重要实验事实，则布朗运动是指（    ）

（A）液体分子的运动        （B）悬浮在液体中的固体分子运动

（C）固体微粒的运动        （D）液体分子与固体分子的共同运动

【答案】

C

 

8．关于能量的转化，下列说法中正确的是（    ）

（A）因为能量守恒，所以“永动机”是存在的

（B）摩擦生热的过程是不可逆过程

（C）空调既能制热又能制冷，说明热传递不存在方向性

（D）因为能的转化过程符合能量守恒定律，所以不会发生能源危机

【答案】

B

 

9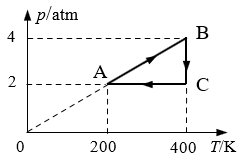．如图表示一定质量的理想气体的状态由A经B、C回到A的p-T图象，下列说法中正确的是（    ）

（A）A→B是等容升温过程

（B）A→B是等容降温过程

（C）B→C是等温压缩过程

（D）C→A是等温膨胀过程

【答案】

A

 

10．一定质量的气体，从一个状态变化到另一个状态，在图所示的4个图中，描述的变化过程可能相同的是（    ）

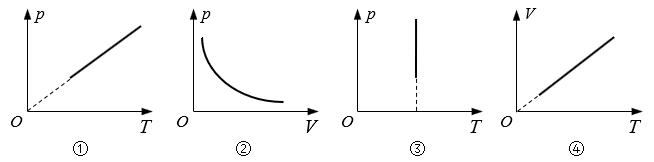
（A）①②        （B）②③        （C）③④        （D）①④

 

【答案】

B

 

11．一定质量的理想气体由状态A经过图中所示过程变到状态B。在此过程中气体的密度（    ）

（A）一直变小            （B）一直变大

（C）先变小后变大     （D）先变大后变小

【答案】

A

【解析】

无

 

12．如图所示，用一个带有刻度的注射器及DIS来探究一定质量气体的压强和体积关系。

（1）所研究的对象是____________；它的体积可用_________直接读出，它的压强是由_________得到。

（2）下表表格中记录了实验中5组数据，根据这些数据在图中作出p-V图线。

实验次数	压强（kPa）	体积（cm3）
1	101.5	20
2	107.5	18
3	123.5	16
4	139.0	14
5	161.5	12

（3）实验过程中，下列哪些操作是错误的？

（A）推拉活塞时，动作要慢。

（B）推拉活塞时，手不能握住注射器筒有气体的部位。

（C）压强传感器与注射器之间的软管脱落后，应立即重新接上，继续实验并记录数据。

（D）活塞与针筒之间要保持润滑又不漏气。

（4）在验证玻意耳定律的实验中，如果用实验所得数据在图所示的p-\(\frac{1}{V}\)图象中标出，可得图中________线。

【答案】

（1）封闭在注射器内的气体，注射器，压强传感器，数据采集器

（2）图略，应为双曲线

（3）C

（4）乙

 

13．在“用单分子油膜估测分子的大小”的实验中：

（1）以下是该实验的操作步骤，请你按合理的操作顺序把步骤的编号填写在横线上：_____________________________________。

A．用测量的物理量估算出油酸分子的直径d。

B．将一滴油酸酒精溶液滴在水面上，待油酸薄膜的形状稳定。

C．用浅盘装入约2cm深的水，然后将痱子粉均匀地撒在水面上。

D．将玻璃板放在浅盘上，用笔将薄膜的外围形状描画在玻璃板上。

E．将画有油膜轮廓的玻璃板放在坐标纸上，测出轮廓内正方形的个数n。

F．用滴管将事先配好浓度的油酸酒精溶液逐滴滴入量筒，记下滴入溶液的体积与滴数。

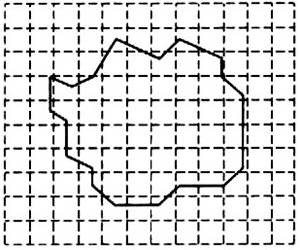（2）若油酸酒精溶液的浓度为每1000 ml溶液中有纯油酸1ml，用注射器测得1 mL上述溶 液有200滴，把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里，待水面稳定后，测得油酸膜的近似轮廓如图所示，图中正方形小方格的边长为1 cm，则每一滴油酸酒精溶液中含有纯油酸的体积是__________mL，油酸膜的面积是_________cm²。根据上述数据，估测出油酸分子的直径是____________m。

【答案】

（1）FCBDEA

（2）5×10^-6，40，1.25×10^-9

 

14．如图所示，在一个玻璃气缸内，用活塞封闭了一定质量的气体，活塞和柄的总质量为m，活塞的面积为S。当活塞自由放置时，气体体积为V。现缓慢地用力向下推动活塞，使气体的体积减少为0.5V，已知大气压强为p₀，求：

（1）活塞自由放置时，气体的压强p₁。

（2）气体的体积减少为0.5V时的压强p₂。

（3）气体的体积减少为0.5V时，加在活塞手柄上的外力F。

【答案】

（1）p₁＝p₀＋\(\frac{{mg}}{S}\)

（2）p₂＝2（p₀＋\(\frac{{mg}}{S}\)）

（3）F＝p₀S＋mg

【解析】

以气缸中的气体为研究对象

（1）p₁＝p₀＋\(\frac{{mg}}{S}\)

（2）因为缓慢推动活塞，所以气缸内气体的温度保持不变，根据玻意耳定律，有

p₁V₁＝p₂V₂

式中，V₁＝V，V₂＝0.5V

得p₂＝2（p₀＋\(\frac{{mg}}{S}\)）

（3）对手柄进行受力分析有：

mg＋F＋p₀S＝p₂S

得：F＝p₀S＋mg

评分说明

本题共6分。其中：

（1）1分；

（2）写出玻意耳定律表达式得1分；算出结果2分；

（3）2分。

 

15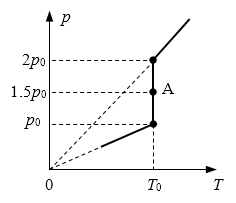．某同学利用DIS实验系统研究一定质量的理想气体的状态变化，在实验后计算机屏幕显示了如下的p－T图象（实线部分），已知在A状态气体体积为V₀。试求实验过程中，当气体温度保持T₀的情况下，气体体积在什么范围内变化？

【答案】

\(\frac{3}{4}\)V₀和\(\frac{3}{2}\)V₀

【解析】

等温条件下，

（1）1.5p₀V₀＝2p₀V₁

V₁＝\(\frac{3}{4}\)V₀

（2）1.5p₀V₀＝p₀V₂

V₂＝\(\frac{3}{2}\)V₀

当气体温度保持T₀的情况下，气体体积在\(\frac{3}{4}\)V₀和\(\frac{3}{2}\)V₀之间变化

 

16．如图所示，一个气缸放置在水平地面上，缸内有一质量可忽略不计的活塞，开始时活塞被两个销钉固定，气缸内封闭气体的压强为 2.4×10⁵ Pa、温度为300K。己知外界的大气压强为 1.0×10⁵ Pa，气缸和活塞均不导热。

（1）若气缸内气体温度升高到 450 K，此时气缸内气体压强为多大？

（2）若保持气缸内气体温度为 450 K 不变，拔去两个销钉，当活塞停止移动时，气缸内气体的体积为原来的几倍？（气缸足够长，活塞与气缸间摩擦不计）

【答案】

（1）p₂ ＝ 3.6×10⁵ Pa

（2）V₃ ＝ 3.6V₂

【解析】

（1）以气缸内封闭气体为研究对象，气缸内气体的体积保持不变，根据查理定律，有

\(\frac{{{p_1}}}{{{T_1}}}\)＝\(\frac{{{p_2}}}{{{T_2}}}\)

式中p₁＝2.4×10⁵Pa，T₁＝300K，T₂＝450K

得p₂＝3.6×10⁵Pa

（2）气缸内气体的温度不变，根据玻意耳定律，有

p₂V₂＝p₃V₃

式中p₂＝3.6×10⁵Pa，p₃＝1.0×10⁵Pa

得V₃＝3.6V₂，即气缸内气体的体积为原来的3.6倍。

 

17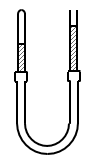．如图所示，下端用橡皮管连接的两根粗细相同的玻璃管竖直放置，右管开口，左管内被封闭气柱长20cm，水银面比右管低15cm，大气压强为75cmHg。现保持左管不动，为了使两管内水银面一样高，则：

（1）右管应向上还是向下移动？

（2）两边液面相平时，气柱长度为多少？

（3）右管管口移动的距离是多少？

【答案】

（1）两管内水银面一样高，左管中空气的压强减小，故体积要增大，右管必须向下移动。

（2）L₂＝24cm

（3）x＝23cm

【解析】

解：（1）两管内水银面一样高，左管中空气的压强减小，故体积要增大，右管必须向下移动。 

（2）左管中气体，p₁＝75+15＝9 0cmHg

V₁＝20S         p₂＝75 cmHg                     V₂＝L₂S

p₁V₁＝p₁V₂

90×20S＝75×L₂S   得L₂＝24 cm

（3）设右管管口向下移动距离为x，通过画图得出关系式

则    \(\frac{{x - 15}}{2}\)＝4，x＝23 cm

还可以这样思考：假设右管先不动，由（2）的结论可知气柱伸长了4 cm，即左管液面下降4 cm，则右管液面上升4 cm，由于原先两液面相差15 cm，因此现在相差23 cm。之后再认为液面相对于玻璃管不动，那么只需将右管向下移动23 cm即可让两液面相平。

 

18．在一篇题为“地球的能量资源”的文章中，提供了到达地球表面太阳辐射能的几个主要去向的数据，如下表所示：

直接反射 （E1）	以热能方式离开 地球（E2）	水循环 （E3）	大气流动 （E4）	光合作用 （E5）
52000×109 kJ/s	81000×109 kJ/s	40000×109 kJ/s	370×109 kJ/s	40×109 kJ/s

（1）根据以上数据分析并计算地球对太阳能的利用率；

（2）每年有多少太阳能通过光合作用转化为化学能？

【答案】

（1）23%

（2）1.26×10²¹ kJ

【解析】

（1）地球获得太阳能的途径有水循环和光合作用这两种，而每秒辐射到地球表面的太阳能应是表中五项的总和。

水循环和光合作用每秒所需太阳能为：E＝E₃+E₅＝40040×10⁹ kJ/s。

每秒辐射到地球表面的总太阳能为：E_总＝E₁+E₂+E₃+E₄+E₅＝173410×10⁹ kJ/s

所以，地球对太阳能的利用率：η＝\(\frac{E}{{{E_总}}}\)＝\(\frac{{40040 \times 10}}{{173410 \times {{10}^9}}}\)＝23%

（2）每年通过光合作用转化为化学能为：

ΔE＝E₅t＝40×10⁹×365×24×3600 kJ＝1.26×10²¹ kJ