1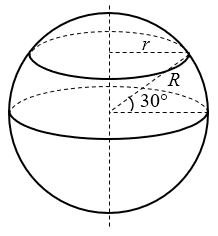．上海的地理纬度约为北纬30^o，地球半径取6.4×10⁶ m，由于地球自转，上海地区地面上的物体随地球自转做圆周运动的角速度和线速度的大小分别为多少？

【答案】

ω＝7.3×10^-5 rad/s，v＝4.0×10² m/s

 

2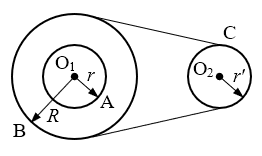．如图所示，转轴O₁上固定有两个半径分别为R和r的轮，用皮带传动O₂轮，O₂的轮半径是r′，若O₁上的两轮每秒钟转了5圈，R＝1 m，r＝r′＝0.5 m，A、B、C分别是三个轮边缘上的点，则：

（1）大轮转动的角速度的大小ω＝_________rad/s；

（2）A、C两点的线速度的大小分别是v_A＝_________m/s，v_C＝_________ m/s。

【答案】

（1）31.4

（2）15.7，31.4

 

3．已知地球质量为M、半径为R，万有引力恒量为G。一颗质量为m的人造卫星，在地面发射架上受到地球的万有引力为___________；当此卫星被发射至距地面5R的高处绕地球运行，它受到地球的万有引力是在发射架上时的______倍。

【答案】

G\(\frac{{Mm}}{{{R^2}}}\)，\(\frac{1}{36}\)

 

4．一个质点沿直径为10 cm的圆周做匀速圆周运动，1秒钟运动了两周，则该质点的周期为________s，角速度大小为________rad/s，线速度大小为__________m/s。

【答案】

0.5，12.56，0.628

 

5．A、B两物体相距L时，它们之间的万有引力为F；当它们相距4L时，万有引力为_________，它们各自所受的万有引力是一对__________________力。

【答案】

F/16，作用力与反作用力

 

6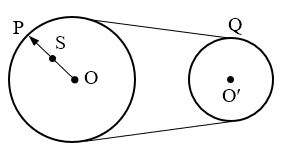．如图所示，大轮通过皮带拉着小轮转动，皮带和两轮之间无滑动，大小轮的半径之比为3∶2，P、Q分别为两轮边缘上的点，S点为大轮半径的中点。则P、Q两点的角速度之比为__________；S、Q两点的线速度的大小之比为__________。

【答案】

2∶3，1∶2

 

7．卡文迪什实验的重大意义在于________________________________________。

【答案】

证实了万有引力定律的正确性，测定了引力常量G的值

 

8．匀速圆周运动是一种（    ）。

（A）匀速运动                   （B）匀加速运动

（C）匀加速曲线运动        （D）变加速曲线运动

【答案】

D

 

9．对于匀速圆周运动的物体，下列说法中错误的是（    ）

（A）线速度不变        （B）角速度不变

（C）周期不变            （D）转速不变

【答案】

A

 

10．如图所示为自行车的链传动示意图，牙盘（大齿轮）和飞轮（小齿轮）用链条相连，A、B分别为牙盘和飞轮边缘上的两点，A、B两点半径分别为r_A、r_B，线速度的大小分别为v_A、v_B，角速度的大小分别为ω_A、ω_B。当自行车牙盘转动时（    ）

（A）因r_A＞r_B，则v_A＞v_B

（B）无论r_A、r_B大小，有v_A＜v_B

（C）因r_A＞r_B，则ω_A＜ω_B

（D）无论r_A、r_B大小，有ω_A＝ω_B

【答案】

C

 

11．地球绕太阳和月球绕地球运行都可近似看作是匀速圆周运动，地球和月球的绕行的角速度之比大约是（    ）

（A）1∶12          （B）12∶1          （C）1∶30          （D）30∶1

【答案】

A

 

12．“直-5”是我国制造的第一种多用途直升机，其起飞时旋翼转速为150 r/min，旋翼直径21 m，则直升机起飞时旋翼转动的角速度多大？旋翼边缘的线速度多大？

【答案】

15.7 rad/s，164.85 m/s

 

13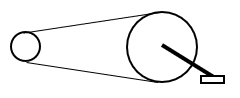．如图所示，自行车上连接踏脚板的连杆长R₁＝20 cm，由踏脚板带动的大齿盘的半径r₁＝10 cm，通过链条链接的小齿盘的半径r₂＝4 cm，后轮半径R₂＝30 cm，小齿盘带动后轮转动使自行车前进。如果脚踏以每分钟30转匀速转动，求：

（1）脚蹬踏脚板的的角速度的大小；

（2）链条传动的速度的大小；

（3）后轮转动的转速。

【答案】

（1）3.14 rad/s

（2）0.314 m/s

（3）1.25 r/s（75 r/min）

 

14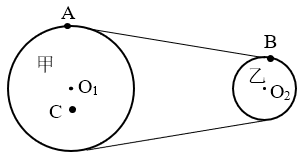．如图所示，甲轮和乙轮半径之比是2∶1，A、B两点分别为甲乙两轮的边缘上的点，C点在甲轮上，它到转轴的距离是甲轮半径的1/3，甲轮以角速度ω转动，皮带不打滑， 求A、B、C三点：

（1）线速度大小之比；

（2）角速度大小之比；

（3）向心加速度大小之比。 

【答案】

（1）3∶3∶1

（2）1∶2∶1

（3）3∶6∶1

【解析】

（1）、（2）因A、B为皮带传动关系，有v_A＝v_B，所以

\(\frac{{{\omega _{\rm{A}}}}}{{{\omega _{\rm{B}}}}}\)＝\(\frac{{{r_{\rm{B}}}}}{{{r_{\rm{A}}}}}\)＝\(\frac{1}{2}\)；

又因A、C同轴转动，有ω_A＝ω_C，所以

\(\frac{{{v_{\rm{A}}}}}{{{v_{\rm{C}}}}}\)＝\(\frac{{{r_{\rm{A}}}}}{{{r_{\rm{C}}}}}\)＝3。

综上结论，有：v_A∶v_B∶v_C＝3∶3∶1；ω_A∶ω_B∶ω_C＝1∶2∶1

（3）因向心加速度a＝\(\frac{{{v^2}}}{r}\)，且r_A∶r_B∶r_C＝6∶3∶2，所以

a_A∶a_B∶a_C＝3∶6∶1

 

15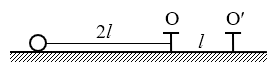．如图所示，光滑水平面上钉有两根相距为l的铁钉O和O′，一段长为2l的细线一端系于O点，另一端连一质量为m的小球，小球位于O′O的延长线上。若小球以垂直于细线，平行于水平面的速度v开始运动，求：

（1）细线接触到铁钉O′后，小球的角速度的大小；

（2）细线接触到铁钉O′后，细线受到的拉力的大小；

（3）小球从开始运动到小球与铁钉O相碰的过程中，所经历的时间。

【答案】

（1）ω′＝\(\frac{v}{l}\)

（2）F＝\(\frac{{m{v^2}}}{l}\)

（3）t_总＝\(\frac{{3\pi l}}{v}\)

【解析】

（1）细线接触到铁钉O′后，小球的线速度大小不变，圆周运动的半径r′＝l，所以小球的角速度大小

ω′＝\(\frac{v}{{r'}}\)＝\(\frac{v}{{l}}\)

（2）细线接触到铁钉O′后，细线的拉力提供小球的向心力，所以细线的拉力大小为

F＝m\(\frac{{{v^2}}}{r′}\)＝\(\frac{{{mv^2}}}{l}\)

（3）以O为圆心做匀速圆周运动过程，运动时间为

t＝\(\frac{T}{2}\)＝\(\frac{{2\pi (2l)}}{{2v}}\)＝\(\frac{{2\pi l}}{v}\)

以O'为圆心做匀速圆周运动过程，运动时间为

t′＝\(\frac{T′}{2}\)＝\(\frac{{2\pi l}}{{2v}}\)＝\(\frac{{\pi l}}{v}\)

所以，运动的总时间：t_总＝t+t′＝\(\frac{{3\pi l}}{v}\)

 

16．特技飞行的飞机在竖直平面内做半径为490 m的圆周运动，飞行员的质量为80 kg。当飞机飞至轨道最高点时，飞行员对座椅的弹力恰好为零，则此时飞机飞行速度的大小为多大？（重力加速度g＝10 m/s²）

【答案】

70 m/s

【解析】

因座椅对飞行员的弹力为零，此时飞行员的重力提供飞行员随飞机做圆周运动的向心力，得

mg＝m\(\frac{{{v^2}}}{r}\)，

v＝\(\sqrt {gR} \)＝\(\sqrt {10 \times 490} \)m/s＝70 m/s

 

17．甲、乙两个质点都作匀速圆周运动，甲的质量是乙的2倍，甲的速率是乙的4倍，甲的圆周半径是乙的2倍，则甲的向心加速度大小是乙的_______倍。甲的向心力大小是乙的________倍。

【答案】

8，16

 

18．如图所示，一圆环圆心为O，若以它的直径AB为轴作匀速转动，圆环上P、Q两点的线速度大小之比是_______；若圆环的半径是20 cm，绕AB轴转动的周期是1 s，环上Q点的向心加速度大小是________m/s²。

【答案】

\(\sqrt 3 \)∶1，0.4π²

【解析】

（1）在同一转体上各质点角速度相同，即ω_P＝ω_Q，两点做圆周运动的半径之比为Rsin60°∶Rsin30°＝\(\sqrt 3 \)∶1，由v＝ωr可知，两点的线速度大小之比为\(\sqrt 3 \)∶1。

（2）a_向＝(\(\frac{{2\pi }}{T}\))²r＝(\(\frac{{2\pi }}{T}\))²Rsin30°＝(\(\frac{{2\pi }}{1}\))²×0.2×0.5 m/s²＝0.4π² m/s²

 

19．我国“嫦娥一号”和“嫦娥二号”绕月行器的圆形轨道距月球表面分别约为200 km和100 km，它们的线速度大小分别为v₁和v₂，v₁、v₂的比值为_______，它们的飞行周期之比T₁∶T₂＝__________。（月球半径取1700 km）

【答案】

\(\sqrt {18} \)∶\(\sqrt {19} \)，\(\sqrt {{{19}^3}} \)∶\(\sqrt {{{18}^3}} \)

 

20．物体做匀速圆周运动时（    ）。

（A）必须受到恒力的作用        （B）所受合力大小可能变化

（C）所受合力必须等于零        （D）所受合力大小不变，方向不断变化

【答案】

D

 

21．关于向心加速度的物理意义，下列说法中正确的是（    ）

（A）它描述的是线速度方向变化的快慢

（B）它描述的是线速度大小变化的快慢

（C）它描述的是向心力变化的快慢

（D）它描述的是角速度变化的快慢

【答案】

A

 

22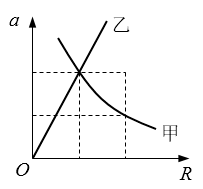．如图所示，反映甲、乙两球分别作匀速圆周运动时向心加速度随半径的变化关系（其中甲的图线是双曲线）。由图像可知（    ）。

（A）甲球运动时，线速度大小是变化的

（B）甲球运动时，角速度大小保持不变

（C）乙球运动时，角速度大小保持不变

（D）乙球运动时，线速度大小保持不变

【答案】

C

【解析】

AB．甲的图线是双曲线，因此a与R成反比，由a＝\(\frac{{{v^2}}}{r}\)可知，甲的线速度应保持不变，选项A、B错误；

CD．乙的图线是正比例图线，即a与R成正比，由a＝ω²R可知，乙的角速度应保持不变，选项C正确。

正确选项为C。

 

23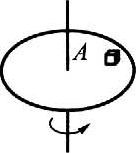．如图所示，小物体A与圆柱保持相对静止，跟着圆盘一起作匀速圆周运动，则A受力情况是受（    ）

（A）重力、支持力

（B）重力、向心力

（C）重力、支持力和指向圆心的摩擦力

（D）重力、支持力、向心力和摩擦力

【答案】

C

 

24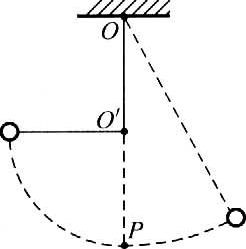．小球用长为l的线悬挂在O点，在O点正下方l/2处有一光滑的钉子O′，把小球拉到与O′在同一水平面的位置并释放，如图所示。当小球第一次通过最低点P时（    ）。

（A）小球速率突然减小

（B）小球的向心加速度突然减小

（C）小球的向心加速度不变

（D）小球受到的向心力突然增大

【答案】

B

【解析】

A．向心加速度只改变速度的方向，不改变速度的大小，因此通过最低点P时，小球的速率并不会发生变化，选项A错误；

BC．在通过P的瞬间，小球的运动半径突然增大，由a_向＝\(\frac{{{v^2}}}{r}\)可知，向心加速度减小，选项B正确、C错误。

D．由F_向＝ma_向可知，向心力突然减小，选项D错误。

正确选项为B。

 

25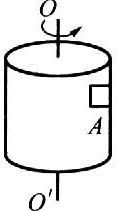．如图所示，半径为r的圆筒绕竖直中心轴OO′转动，小物块A靠在圆筒的内壁上，它与圆筒的摩擦因数为μ，现要使A不下落，则圆筒转动的角速度ω至少应为多大？

【答案】

\(\sqrt {\frac{g}{{\mu r}}} \)

【解析】

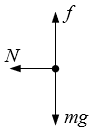A物块的受力如图所示，内壁对A的弹力作为向心力，由正交分解法可得：

竖直方向：mg＝f＝μN               （1）

水平方向：N＝mω²r                  （2）

由（1）得：N＝\(\frac{{mg}}{\mu }\)，代入（2）式，得：ω＝\(\sqrt {\frac{g}{{\mu r}}} \)。