1．当汽车突然刹车停止时，汽车里的乘客会向前倾倒，这是因为汽车已经停止而乘客由于惯性要保持原来的运动速度前进。由此可以推断出，汽车突然停止时，汽车没有惯性，乘客才有惯性。判断这个推断是否正确，并简述理由。

【答案】

认为乘客有惯性是正确的；而汽车没有惯性是不正确的。因为汽车突然停止是受到阻力的结果，阻力改变了其运动状态。如果没有收到阻力，汽车不会停止，说明汽车是有惯性的。

【解析】

惯性是物体的一种属性，无论物体的体积大小如何、处于何种运动状态，一切有质量的物体都有惯性。而物体运动状态是否变化，却不能由物体本身的惯性来决定，而是看物体所受的合外力。分析汽车：汽车停止，是因为汽车刹车过程中汽车受到的合外力不外零，汽车的运动状态由运动变为静止，这个过程中汽车总要滑行一段距离，也是由汽车的惯性引起的。分析乘客：乘客的脚与车厢间存在摩擦力，随着汽车运动状态的改变而改变，而乘客的上身由于惯性要保持原来的运动，因此，突然刹车时汽车里的乘客会向前倾。

 

2．磁悬浮列车是连接上海浦东国际机场的重要交通工具之一，列车运行最高时速430 km/h。若列车从车站开出，可视作匀加速直线运动，经过3 min就可达最高时速。则一位质量为60 kg的乘客在列车加速过程中受到合力有多大？

【答案】

39.6 N

【解析】

用牛顿第二定律解决实际问题常常与运动学规律紧密联系，加速度a是力与运动之间联系的纽带。本题已知磁悬浮列车的运动情况，可先通过运动学公式求出加速度，然后运用牛顿第二定律求出乘客的受力情况。

列车加速后的末速度大小v＝430 km/h≈119.4 m/s。

根据v＝at，其加速度大小a＝\(\frac{v}{t}\)＝\(\frac{{119.4}}{{3 \times 60}}\)m/s²≈0.66 m/s²

因乘客的加速度大小与列车相同，根据牛顿第二定律，乘客受到的合外力F＝ma＝60×0.66 N＝39.6 N。

 

3．如图所示，一小孩坐在雪橇上，他们的总质量为40 kg，大人用大小为50 N、方向与水平面θ＝37°角斜向上的拉力拉雪橇，使其由静止开始运动。设雪橇和小孩受到的阻力为20 N。（sin37°＝0.6，cos37°＝0.8）求：

（1）雪橇和小孩运动的加速度大小；

（2）经过4 s雪橇在雪地留下的痕迹的长度。

【答案】

（1）a＝0.5 m/s²

（2）s＝4 m

【解析】

分析：运用牛顿第二定律解题的一般步骤：先确定研究对象，再对研究对象进行受力分析和运动状态分析，最后运用牛顿第二定律和运动学公式求解。本题研究对象为雪橇和小孩整体，对雪橇和小孩的受力分析如图所示，因拉力F斜向上，对F进行正交分解，其在水平方向的分力为Fcosθ，最后建立方程可求出加速度的大小。

解答：（1）对雪橇和小孩的受力分析如图所示，以雪橇运动方向为正方向，根据牛顿第二定律得Fcos37°－f＝ma，所以

a＝\(\frac{{F\cos 37^\circ  - f}}{m}\)＝\(\frac{{50 \times 0.8 - 20}}{{40}}\)m/s²＝0.5 m/s²。

（2）根据位移公式s＝\(\frac{1}{2}\)at²＝\(\frac{1}{2}\)×0.5×4² m＝4 m。

 

4．惯性是物体的一种属性，他与物体的运动状态_________（选填“有关”或“无关”），_________是惯性大小的量度。

【答案】

无关，质量

 

5．如图所示，两位同学用弹簧测力计在电梯中做实验。他们先将测力计挂在固定于电梯壁的钩子上，然后将一质量为0.5 kg的物体挂在测力计挂钩上。若电梯上升时测力计的示数为6 N，则电梯加速度的大小为______m/s²，加速度方向向________（选填“上”或“下”）。

【答案】

2，上

【解析】

无

 

6．一艘在太空中的宇宙飞船，开动推进器后受到的推力为900 N，开动3 s后速度增加了0.9 m/s，则宇宙飞船的质量为_________kg。

【答案】

3000

 

7．一个质量为2 kg的物体受到几个共点力的作用处于静止状态，若同时撤去一个方向向东、大小为3 N的力和一个方向向北、大小为4 N的力，物体的加速度大小为_________m/s²，物体运动的方向为_________。

【答案】

2.5，南偏西37°

 

8．用2 N的水平力拉一个物体沿水平面运动时，物体可获得1 m/s²的加速度；用3 N的水平力拉物体沿原地面运动，加速度是2 m/s²，那么改用4 N的水平力拉物体，物体在原地面上运动的加速度是______m/s²，物体在运动中受滑动摩擦力大小为______N。

【答案】

3，1

 

9．伽利略的理想斜面实验（如图所示）的意义在于（    ）。

（A）证明了力是维持物体运动的原因

（B）证明了沿斜面滚下的小球，到了水平面上就做匀速直线运动

（C）证明了沿斜面滚下的小球，能滚到另一个斜内面上相同的高度

（D）证明了维持物体运动不需要力

【答案】

D

 

10．下列单位中属于国际单位制的基本单位的是（    ）。

（A）千克            （B）牛顿            （C）米/秒           （D）米/秒²

【答案】

A

 

11．根据牛顿运动定律，以下选项中正确的是（    ）

（A）人只有在静止的车厢内，竖直向上高高跳起后，才会落在车厢的原来位置

（B）人在沿直线匀速前进的车厢内，竖直向上高高跳起后，将落在经起点的后方

（C）人在沿直线加速前进的车厢内，竖直向上高高跳起后，将落在起跳点的后方

（D）人在沿直线减速前进的车厢内，竖直向上高高跳起后，将落在起跳点的后方

【答案】

C

【解析】

由于物体具有惯性，人在静止或沿直线匀速前进的车厢内，竖直向上高高跳起后都会落在车厢的原来位置，A、B错；人在沿直线加速前进的车厢内，竖直向上高高跳起后将落在起跳点的后方，C对；人在沿直线减速前进的车厢内，竖直向上高高跳起后，将落在起跳点的前方，D错。

 

12．原来静止在光滑水平面上的物体，在刚受到一个水平力作用的瞬间（    ）

（A）物体立刻获得加速度，但速度仍等于零

（B）物体立刻获得速度，但加速度为零

（C）物体立刻获得加速度，也同时也获得速度

（D）物体的加速度和速度都要经过少许时间才能获得

【答案】

A

 

13．如图，一个倾角为α的光滑斜面，在水平面上向右做匀加速直线运动，物体m与斜面保持相对静止，重力加速度为g，则斜面运动的加速度为（    ）

（A）gsinα           （B）gcosα           （C）gtanα           （D）gcotα

【答案】

C

【解析】

无

 

14．下列关于力学发展的事例中符合史实的（    ）。

（A）牛顿三大运动定律是经典力学体系的基础

（B）牛顿力学能适用微观领域中的力学现象

（C）牛顿力学提出光速是自然界中速度的极限

（D）相对论的提出否定了牛顿力学

【答案】

A

 

15．如图（a）所示为利用DIS做验证牛顿第三定律实验的操作示意图，该实验所用的传感器为____________。图（b）为实验时在电脑显示屏界面上出现的结果，观察图（b）我们可以得出关于作用力与反作用力关系的结论是________________________。

【答案】

力传感器，大小时时相等、方向相反、同时产生同时消失

 

16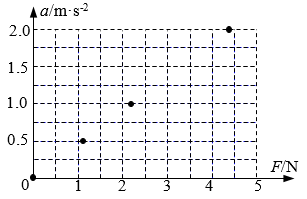．在“用DIS研究加速度与力的关系、加速度与质量的关系”实验中，保持小车质量不变，改变小车所受的作用力，测得了下表所示的5组数据，并已在坐标平面上画出部分数据点，如图所示：

组别	1	2	3	4	5
F/N	0	1.1	2.2	3.3	4.4
a/m·s-2	0	0.5	1.0	1.5	2.0

（1）在图中画出第4组数据对应的数据点，然后作出a-F的关系图线；

（2）由所作图线可以得到结论：在质量一定的情况下，加速度a与作用力F成________比；

（3）当研究加速度与质量的关系时，应保持___________不变，改变小车的质量来进行实验。

【答案】

（1）见图

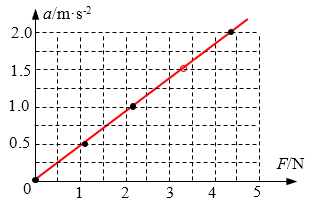
（2）正

（3）小车受到的作用力

【解析】

无

 

17．在“用DIS实验研究加速度与质量的关系”实验中，我们用了如图所示的装置，请完成下列问题：

（1）下列做法中正确的是（    ）

（A）要控制小车和钩码的质量都不变

（B）要控制小车的质量不变，改变钩码的质量

（C）要控制钩码的质量不变，改变小车的质量

（D）小车和钩码的质量都要改变

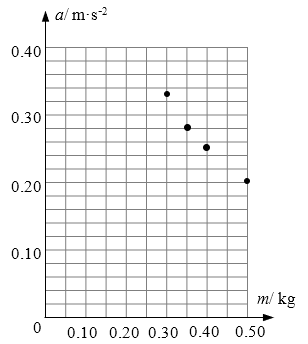（2）实验中测得了下表所示的五组数据，并已在坐标平面上画出部分数据点，在图中画出第四组数据对应的数据点，然后作出a-m的关系图像；

组别	1	2	3	4	5
a（m·s-2）	0.33	0.28	0.25	0.22	0.20
m（kg）	0.30	0.35	0.40	0.45	0.50

（3）为进一步确定加速度与质量的关系，应画a-_________图像；

（4）本实验得到的结论是________________________________________。

【答案】

（1）C

（2）略

（3）1/m

（4）在受力不变时，小车的加速度与其质量成反比

 

18．据报载，随着磁浮技术的发展，将来可能设计利用磁浮技术起飞的飞机，起飞速度可以达到150 m/s。假设飞机的总质量为5×10³ kg，沿水平直轨道以2 m/s²的加速度由静止开始匀加速运动达到最大速度，且不考虑阻力。求 ：

（1）飞机所需动力F的大小；

（2）飞机由静止至最大速度所用时间t及滑行的位移s。

【答案】

（1）1×10⁴ N

（2）75 s，5625 m

 

19．如图所示，质量为60 kg的滑雪运动员，在倾角为30°的斜坡顶端从静止开始匀加速下滑90 m到达坡底，用时10 s，求：

（1）运动员下滑过程中的加速度大小；

（2）运动员到达坡底时的速度大小；

（3）运动员下滑过程中所受阻力的大小。

【答案】

1.8 m/s²，18 m/s，192 N

 

20．如图（a），用升降机从静止开始竖直向上搬运重为50 N的物体，物体相对升降机静止。若物体所受弹力F与时间t的变化关系如图（b）所示，试分析说明物体在各段时间内做什么运动？

【答案】

（1）在0~3 s内，因弹力F大于重力且不变，所以物体向上做匀加速运动；

（2）在3~10 s内，因弹力F等于重力，所以物体向上做匀速运动；

（3）在10~13 s内，因弹力F小于重力且不变，所以物体向上做匀减速运动。

 

21．在平直轨道上行驶列车的车厢顶板上，用细线悬挂着一个小球，如图所示，在下列情况下可对列车的运动情况得出怎样的判断？

（1）细线竖直：____________________________；

（2）细线向左方偏斜：____________________________；

（3）细线向右方偏斜：____________________________。

【答案】

（1）列车向左或向右匀速运动。

（2）列车做向右加速或向左减速运动。

（3）列车做向左加速或向右减速运动。

【解析】

应先对小球进行受力分析，作用在小球上的力只有两个：地球对它的重力mg，细线对它的拉力F_T。根据这两个力的合力，可判断小球的加速度方向，从而可知车厢的加速度方向，但无法推断车厢的运动方向，因此本题有多解。

（1）当细线竖直时，小球所受的重力mg与细线对它的拉力F_T在一直线上，且沿竖直方向。根据题意车厢不可能在竖直方向上运动，因此小球必处于受力平衡，行驶的列车做匀速直线运动。

（2）细线向左方偏斜时，小球所受的重力mg与细线对它的拉力F_T不在一直线上，小球一定受到向右的水平合外力作用，产生水平向右的加速度，由此可以判断出列车一定有向右的加速度。然而列车的运动方向未知，因此，无法确定列车是做向右加速还是向左减速运动。

（3）分析方式如同（2）中叙述。

 

22．一质量为m＝60 kg的学生在听到火警信号时利用逃生器从高h＝8 m的楼上沿绳子从静止开始下滑，开始时他通过控制逃生器使自己匀加速下滑，此时逃生器与绳子间的摩擦力为360 N。问下滑1 s时该学生的速度多大？这位学生下滑1 s后调节逃生器与绳子间的摩擦力，使自己做匀减速运动，到达地面时速度恰好为零，问减速运动过程逃生器与绳子间的摩擦力的大小为多少？（假设逃生器质量不计，重力加速度g取10 m/s²）

【答案】

4 m/s；680 N

【解析】

设以竖直向下为正方向，学生沿绳子开始下滑1 s内，对学生受力分析如图所示，根据牛顿第二定律得

mg－F_f＝ma₁

a₁＝\(\frac{{mg - {F_f}}}{m}\)＝\(\frac{{600 - 360}}{{60}}\)m/s²＝4 m/s²

1 s末的速度   v＝a₁t＝4×1 m/s＝4 m/s

学生开始1 s内下降的距离

s＝\(\frac{1}{2}\)a₁t²＝\(\frac{1}{2}\)×4×1² m＝2 m

在减速运动过程中，末速度v_t＝0，设位移s′＝h－s，在减速运动过程中对学生的受力分析如图所示

由v_t²－v₀²＝2as′

a₂＝\(\frac{{0 - {v^2}}}{{2(h - s)}}\)＝\(\frac{{ - {4^2}}}{{2 \times (8 - 2)}}\) m/s²＝－\(\frac{4}{3}\)m/s²

根据牛顿第二定律F_f′－mg＝ma₂

F_f′＝ma₂+ mg＝（60×\(\frac{4}{3}\) + 60×10）N＝680 N

所以，学生下滑1 s时速度大小为4 m/s；减速过程中逃生器与绳子间的摩擦力的大小为680 N。

 

23．一位同学住在21层高楼，每天乘电梯上下楼。他利用实验仪器，得到电梯从21楼直达1楼的速度－时间图象如图所示。根据图象可知，在0～4 s这段时间内，这位同学处于____（选填“超重”或“失重”）状态。若这位同学的质量为54 kg，那么在0～4 s这段时间内，他受到的支持力为____N。

【答案】

失重，472.5

 

24．如图所示的a-F图像中，实线甲和乙分别表示在两地、各自在保持物体质量不变的情况下，用竖直向上的力匀加速提升物体时，物体加速度a的大小与拉力F的大小之间的关系。由图可以判断甲地的重力加速度________乙地的重力加速度，甲地的物体质量________乙地的物体质量（选填“＞”、“＝”或“＜”）。

【答案】

＜，＜

【解析】

由牛顿第二定律可得：

F－mg＝ma

把上式变换成一次函数的形式：

a＝\(\frac{1}{m}\)F－g

由上式可以看出：a-F图像的斜率表示质量的倒数\(\frac{1}{m}\)，截距表示－g。因此从图线中可以看出g_甲＜g_乙，m_甲＜m_乙。

 

25．某人在以2 m/s²的加速度加速下降的升降机中，最多能举起80 kg的物体，那么他在地面上最多能举起_____kg的物体；若此人在另一升降机中最多能举起40 kg的物体，则此升降机运动的加速度大小为______m/s²，方向向____。（g取10 m/s²）

【答案】

64，6，上

 

26．一滑块以4 m/s的速度在光滑水平面上向左滑行。从某一时刻起，滑块受一大小为4 N，方向向右的水平力，经过4 s滑块的运动方向变为向右，速度大小仍为4 m/s。则这段时间内滑块水平位移为_________m，滑块的质量为_________kg。

【答案】

0，2

 

27．在某停车场，甲、乙两辆同型号的车发生了碰撞事故。甲车司机背部受伤，乙车司机胸部受伤。根据两位司机的伤情，则可以判定（    ）。

（A）甲车车头撞了静止的乙车车尾

（B）甲车车尾撞了静止的乙车车尾

（C）乙车车头撞了静止的甲车车尾

（D）乙车车头撞了静止的甲车车头

【答案】

C

 

28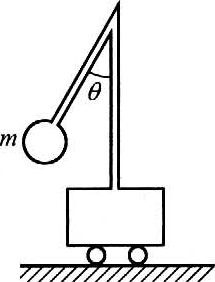．如图所示，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆下端固定一质量为m的小球，杆对球的作用力为F，则小车（    ）

（A）静止时，F＝mgcosθ，方向沿斜杆向上

（B）以水平向右加速度a运动时，F＝mg/cosθ，方向沿斜杆向上

（C）以水平向右加速度a运动时，F＝mg/sinθ，方向垂直斜杆向上

（D）以水平向右加速度a运动时，F=\(\sqrt {{{(ma)}^2} + {{(mg)}^2}} \)，方向斜向右上方，与竖直方向的夹角为α＝arctan\(\frac{a}{g}\)

【答案】

D

【解析】

杆的作用力不一定沿杆方向！从选项A中可以很容易证明这一点，根据两力平衡的条件，杆的力F＝mg，方向竖直向上（并不沿杆方向）。选项A错误。

选项BCD：两力加速并不需要用到正交分解法，用平行四边形定则就够了，受力分析如图所示，根据勾股定律：

F＝\(\sqrt {{{(F_合)}^2} + {{(mg)}^2}} \)＝\(\sqrt {{{(ma)}^2} + {{(mg)}^2}} \)

由三角函数，有

tanα＝\(\frac{{{F_合}}}{{mg}}\)，解得α＝arctan\(\frac{a}{g}\)

选项D正确。

 

30．雨滴从高空由静止下落，由于受到的空气阻力随雨滴速度的增大而增大，在此下落过程中雨滴的（    ）

（A）加速度不断减小，速度不断减小

（B）加速度不断减小，速度不断增大，加速度为零时，速度最大

（C）雨滴经历先加速后匀速再减速运动

（D）速度的变化越来越小

【答案】

B

 

31．利用DIS系统和力传感器可以测量快速变化的力的瞬时值。如图是用这种方法获得的弹性绳中拉力F随时间t的变化图线。实验时，把小球举高到绳子的悬点O处，然后放手让小球自由下落。由图线所提供的信息，可得（   ）

（A）t₁时刻小球速度最大

（B）t₂时刻小球速度最大

（C）t₁~t₂期间小球速度先增大后减小

（D）t₁与t₃时刻小球的速度相同

【答案】

C

【解析】

此过程的完整分析：t₁时刻弹性绳刚被拉伸，此时小球重力G大于F，仍向下做加速度运动，随着弹性绳的形变越来越大，在t₁～t₂期间有F＝G，此时小球速度最大，但由于惯性，小球继续向下做减速运动，直至t₂时刻运动至最低点，此时F最大，之后小球会向上弹回。所以选项A、C错误。

此题容易错选D，根据对称性可知速度大小相同，但方向相反。

 

31．质量为2kg的物体在水平推力F的作用下沿水平面作直线运动，一段时间后撤去F，其运动的v-t图像如图所示。g取10m/s²，求：

（1）物体与水平面间的滑动摩擦系数μ；

（2）水平推力F的大小；

（3）0～10s内物体运动位移的大小。

【答案】

（1）0.2

（2）6N

（3）46m

【解析】

 

 

33．风洞实验室中可以产生水平方向的、大小可调节的风力，现将一套有小球的细直杆放入风洞实验室，小球孔径略大于细杆直径。

（1）当杆在水平方向上固定时，调节风力的大小，使小球在杆上作匀速运动，这时小球所受的风力为小球所受重力的0.5倍，求小球与杆间的滑动摩擦因数。

（2）保持小球所受风力不变，使杆与水平方向间夹角为37°并固定，则小球从静止出发在细杆上滑下距离s所需时间为多少？（sin37°＝0.6，cos37°＝0.8）

【答案】

（1）0.5

（2）\(\sqrt {\frac{{8s}}{{3g}}} \)

【解析】

（1）设小球所受的风力为F，小球质量为m

F＝μmg

μ＝\(\frac{F}{{mg}}\)＝\(\frac{0.5mg}{{mg}}\)＝0.5

（2）设杆对小球的支持力为N，摩擦力为f

沿杆方向Fcosθ＋mgsinθ－f＝ma

垂直于杆方向N＋Fsinθ－mgcosθ＝0

f＝μN

可解得

a＝\(\frac{{F\cos \theta  + mg\sin \theta  - f}}{m}\)＝（g＋\(\frac{{{F^2}}}{{{m^2}g}}\)）sinθ＝\(\frac{3}{4}\)g

s＝\(\frac{1}{2}\)at²

t＝\(\sqrt {\frac{{2s}}{{\frac{3}{4}g}}} \)＝\(\sqrt {\frac{{8s}}{{3g}}} \) 

 

34．如图所示，用AB、BC两根细绳把质量为m＝1 kg的小球悬挂于车内，AB绳与竖直方向的夹角为α＝37°，BC绳与竖直方向的夹角为β＝53°。当小车向右做加速度不断增大的加速运动时，试分析AB、BC两绳的拉力变化情况。（重力加速度g取10 m/s²，sin37°＝0.6，cos37°＝0.8）

【答案】

当加速度a由零逐渐增大时，小球受到的水平向右的合力要不断增大，所以F_AB将不断增大；又因为小球竖直方向的合力为零，且小球重力不变，所以F_CB将不断减小。

当加速度增大到a＝gtanα＝7.5 m/s²时，F_CB＝0；F_AB＝mg/cosα＝12.5 N。接着，加速度继续增大，则有细绳BC松掉，小球飞起，α角增大，F_AB＝mg/cosα随着α角的增大而继续增大。