1．关于质点的加速度，下列说法中正确的是（    ）

（A）加速度越大，质点运动越快

（B）加速度越大，质点的速度变化越快

（C）加速度不变，质点的运动快慢保持不变

（D）加速度为零，质点的速度也为零

【答案】

B

【解析】

加速度是描述速度变化快慢的物理量，加速度越大表明物体的速度变化越快；加速度不变表明物体的速度随时间均匀变化；加速度为零表明物体的速度保持不变。

 

2．做初速为零的匀加速直线运动的物体，第1 s内位移是2 m。求 ：

（1）10 s内位移的大小；

（2）第10 s内位移的大小；

（3）10 s末速度的大小。

【答案】

（1）s₁₀＝200 m

（2）Δs₁₀＝38 m

（3）v₁₀＝40 m/s

【解析】

（1）s₁＝\(\frac{1}{2}\)at₁²，将s₁＝2 m、t₁＝1 s代入，即可求得a＝4 m/s²。

10 s内位移：s₁₀＝\(\frac{1}{2}\)at₁₀²＝×4×10² m＝200 m

（2）9 s内位移：s₉＝\(\frac{1}{2}\)at₉²＝×4×9² m＝162 m

第10 s内的位移：Δs₁₀＝s₁₀－s₉＝（200－162）m＝38 m

（3）10 s末的速度：v₁₀＝at₁₀＝4×10 m/s＝40 m/s

 

3．有甲、乙两个物体，从同一地点，同方向、同时由静止开始做匀加速直线运动，经相同时间它们的位移之比为9∶4，则它们经相同位移的时间之比为______，速度之比为_____。

【答案】

2∶3，3∶2

【解析】

根据初速度为零的匀加速直线运动的位移公式s＝\(\frac{1}{2}\)at²，对甲、乙两个物体，在相同时间内位移的大小之比\(\frac{{{s_甲}}}{{{s_乙}}}\)＝\(\frac{{{a_甲}}}{{{a_乙}}}\)＝\(\frac{9}{4}\)，经过相同的位移所用时间之比\(\frac{{{t_甲}}}{{{t_乙}}}\)＝\(\frac{{\sqrt {{a_乙}} }}{{\sqrt {{a_甲}} }}\)＝\(\frac{2}{3}\)；根据速度和位移的关系式v²＝2as，经过相同的位移时，速度的大小之比\(\frac{{{v_甲}}}{{{v_乙}}}\)＝\(\frac{{\sqrt {{a_甲}} }}{{\sqrt {{a_乙}} }}\)＝\(\frac{3}{2}\)。

 

4．某汽车从静止出发做匀加速直线运动，经过12 s后改做匀速直线运动，又经过8 s，汽车已前进的总位移为336 m。求：

（1）该汽车加速阶段的加速度。

（2）画出该汽车运动的速度-时间图像。

【答案】

（1）a＝2m/s²

方向与汽车运动方向一致。

（2）如图所示。

【解析】

（1）s₁＝\(\frac{1}{2}\)at₁²，代入数据后可得

s₁＝72a……①

s₂＝vt₂＝at₁t₂，代入数据后可得

s₂＝96a……②

将①、②两式相加可得s₁+s₂＝168a，即336＝168a，所以解得加速度的大小

a＝2m/s²

方向与汽车运动方向一致。

（2）汽车匀加速运动的末速度大小，即匀速运动的速度大小

v＝v_t＝ at₁＝2×12m/s＝24m/s

得到的v－t图像如图所示。

 

5．质点从A出发向正东方向移动了4 m到达B，再从B出发向正北方向移动了3 m到达C，则质点从A到C的路程为_____m；位移的大小为____m，方向为______。

【答案】

7，5，东偏北37°

 

6．物体从静止出发做匀加速直线运动，测得它经过8 m位移用了4 s时间，则该物体运动的加速度大小为___m/s²；4 s末的瞬时速度的大小为_____m/s。

【答案】

1，4

 

7．在地球上做自由落体运动的物体，着地速度是20 m/s，则该物体是从_____m高处下落的。如果是在月球上则是从______m高处落下的（月球上落体加速度是地球上的\(\frac{1}{6}\)）。

【答案】

20，120

 

8．某同学在正在加速起步的汽车中观察速度计时，发现它的指针随时间均匀增加到如图所示的位置，所用的时间是6 s。则此时汽车行驶的路程为_______m。此后汽车改做匀速直线运动，又运动了20 s，在这26 s时间内汽车的平均速度为_______m/s。

【答案】

50，14.74

 

9．关于质点的描述，下列说法中正确的是（    ）

（A）质量很小的物体必定可以看作质点 （B）体积很小的物体必定可以看作质点

（C）某些情况下，地球也可以看作质点 （D）研究乒乓球旋转快慢时，可以把它看作质点

【答案】

C

 

10．关于速度和加速度的关系，下列说法中正确的是（    ）

（A）加速度可以用速度与时间的比值来表示 （B）速度改变量越大，加速度越大

（C）加速度越大，速度变化越快     （D）速度为零时，加速度一定也为零

【答案】

C

 

11．一辆汽车由静止开始做匀加速直线运动，从开始运动到驶过第一个100 m距离时，速度增加了10 m/s，汽车驶过第二个100 m时，速度的增加量（     ）

（A）小于10 m/s        （B）等于10 m/s         （C）大于10 m/s         （D）无法确定

【答案】

A

 

12．滑雪运动员从雪坡上静止起下滑至水平面（阻力不计），下列能较正确反映这一运动的v-t图象。是图中的（    ）

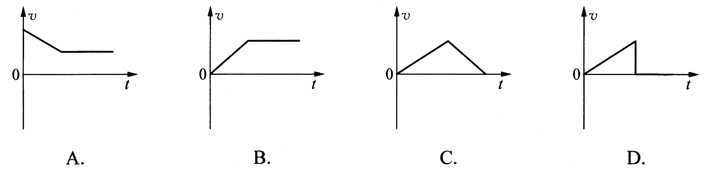
【答案】

B

 

13．现代实验技术——数字化信息系统（DIS）通常由______、_______和________三部分组成。在测定小车运动的平均速度时选用的是_______传感器。在测定小车瞬时速度时常用______传感器。如图所示是实验时记录的小车运动的位移随时间变化的图象，选择区域AB范围内平均速度为________m/s；选择区域AC范围内平均速度为_______m/s。其中较接近A点瞬时速度为______（选填“前者”或“后者”）。

【答案】

传感器，数据采集器，计算机，位移，光电门，1.17，1.0，后者

 

14．如图所示是用光电门传感器测定小车瞬时速度的情景，某同学采用不同的挡光片做了三次实验，研究小车经过光电门的瞬时速度，并对测量精确度加以比较。

次数	挡光片宽（m）	挡光时间（s）	速度（m/s）
1	0.080	0.036
2	0.040		2.00
3	0.020	0.0105

（1）每次释放小车的位置应当_______；

（2）测量的是小车前端P抵达_______点（选填a、b或c）（ac间距离恰等于小车长度）的瞬时速度；

（3）由上述表格可知测得瞬时速度较精确的值为_____m/s。

【答案】

（1）相同

（2）b

（3）1.90（表格中：2.22，0.020，1.90）

 

15．从静止开始做匀加速直线运动的物体，求：

（1）它在第n s内的位移与前n s内位移之比是多少?

（2）它在第n s末的速度与前n s内平均速度之比是多少?

【答案】

（1）(2n-1)∶n²

（2）2∶1

 

16．一把长1 m的直尺靠近墙壁自某高处自由下落，经过墙上一个钉子的时间为0.1 s，求释放前直尺上端到钉子的距离。

【答案】

5.51 m

 

17．质点做匀加速直线运动，初速度是5 m/s，加速度是1 m/s²，那么在第4 s末瞬时速度的大小是________m/s，第4 s内位移的大小是_______m。

【答案】

9，8.5

【解析】

根据匀变速直线运动的速度公式v_t＝v₀+at可直接求解第4 s末的瞬时速度。第4 s内的位移可用位移公式s＝v₀t+\(\frac{1}{2}\)at²先分别求出前4 s和前3 s内的位移，两者相减即为第4 s内的位移。

 

18．一个物体作竖直上抛运动回到原处，下列说法中正确的是（    ）

（A）上升过程和下降过程的位移相同

（B）上升到最高点时，瞬时速度和加速度都为零

（C）运动过程中，任何相等时间内的速度变化量都相等

（D）运动过程中，相等时间内的位移可能相等

【答案】

C

【解析】

在物体上升和下降过程中的路程相等，但位移方向不同，故A不对；在最高点时，瞬时速度为零，加速度为重力加速度g，故B不对；竖直上抛运动是加速度为重力加速度g的匀变速运动，所以任何相等时间内的速度变化量都相等，故C正确；上升过程中物体作匀减速直线运动，相等时间内的位移不可能相等，下降过程物体作匀加速度直线运动，相等时间内的位移也不可能相等，上升与下降过程相比，因为位移方向不同，可能会有相等的时间内路程相等，但位移不可能相等，所以D不对。

 

19．一列火车的初速度为12 m/s。制动后作匀减速运动，测得3 s内位移是30 m，这时火车仍在运动。求火车从开始制动起经过10 s后位移是多少？

【答案】

54 m

【解析】

设火车作匀减速运动的加速度大小为a，

s₁＝v₀t₁－\(\frac{1}{2}\)at₁²，

将s₁＝30 m、v₀＝12 m/s、t₁＝3 s代入，可求出

a＝\(\frac{4}{3}\) m/s²

设火车开始制动后经过t₂时间会停止，则

t₂＝\(\frac{{{v_t} - {v_0}}}{a}\)＝\(\frac{{0 - 12}}{{ - 4/3}}\)s＝9 s

所以火车开始制动后经过10 s的位移就是减速到停止的位移，所以

s₂＝\(\frac{{v_t^2 - v_0^2}}{{2a}}\)＝\(\frac{{0 - 144}}{{ - 8/3}}\)＝54 m

火车从开始制动起经过10 s后位移的大小为54 m，方向与火车运动方向一致。

 

20．一辆汽车从静止起以加速度a₁做匀加速运动，经一定时间后关闭发动机以加速度a₂做匀减速运动，直到停止。该车的总位移为s。该车全程所花时间是多少？

【答案】

\(\sqrt {2s(\frac{{{a_1} + {a_2}}}{{{a_1}{a_2}}})} \)

【解析】

设汽车作匀加速运动的位移为s₁、时间为t₁、加速度大小为a₁，作匀减速运动的位移为s₂、时间为t₂、加速度大小为a₂，车全程所花的时间为t。汽车全过程的v-t图象如图所示。

在v-t图象中面积的物理意义是位移，所以s＝\[\frac{1}{2}\]vt，可得

v＝\(\frac{{2s}}{t}\)

根据加速度的表达式有：t₁＝\(\frac{v}{{{a_1}}}\)，t₂＝\(\frac{v}{{{a_2}}}\)

t＝t₁＋t₂＝\(\frac{v}{{{a_1}}}\)＋\(\frac{v}{{{a_2}}}\)＝v\(\frac{{{a_1} + {a_2}}}{{{a_1}{a_2}}}\)

将v＝\(\frac{{2s}}{t}\)代入上式，可得车全程所花时间t＝\(\sqrt {2s(\frac{{{a_1} + {a_2}}}{{{a_1}{a_2}}})} \)

启示：对末速度为零的匀减速运动，可以根据对称的思想，将其视为反向的匀加速直线运动；对这类由静止开始，先做匀加速运动再做匀加速运动的问题，可以画出v-t图像，利用图形的面积（其物理意义为位移）、和图线的斜率（其物理意义为加速度），是一种常用的方法。

 

21．已知某质点做匀减速直线运动，其初速度为10 m/s，加速度的大小为2 m/s²，则它在第3 s初的速度大小为_____________m/s，在第3 s内的位移大小为______________m。

【答案】

6，5

 

22．以初速度v₀竖直上抛一小物体，物体上升一半时间时的瞬时速度大小为_______，物体上升的最大高度为___________。

【答案】

\(\frac{{{v_0}}}{2}\)，\(\frac{{v_0^2}}{{2g}}\)

 

23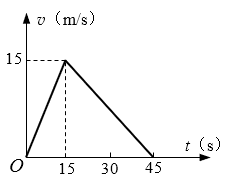．一个物体从静止开始沿一直线运动，先做匀加速运动，接着做匀减速运动，最后静止，其速度图像如图所示。在0～15s和15s～45s两段时间内位移大小之比为_________；平均速度大小之比为___________。

【答案】

1∶2，1∶1

 

24．某物体先以恒定加速度a₁从静止开始运动，一段时间后又以恒定加速度a₂运动，经过和前一段运动相同的时间后物体恰好回到原处，则前后两段运动的加速度之比为__________，前后两段运动结束时的末速度之比为__________。

【答案】

1∶3，1∶2

【解析】

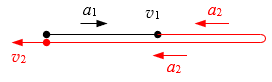（1）设时间为t，前半段的位移为s，由运动学公式，对前半段（如图中黑色线段）可得：

s＝\(\frac{1}{2}\)a₁t²                      （1）

后半端先做加速度大小为a₂匀减速直线运动，速度为零时，反向做加速度大小为a₂的匀加速直线运动，整个过程a₂的大小方向都不变，可以统一看做一个匀变速直线运动（类似于竖直上抛运动，如图中红色线段），可得：

－s＝v₁t－\(\frac{1}{2}\)a₂t²＝(a₁t)t－\(\frac{1}{2}\)a₂t²         （2）

两式联立可得：

\(\frac{1}{2}\)a₁t²＝\(\frac{1}{2}\)a₂t²－a₁t²

a₁∶a₂＝1∶3

（2）前半段有：v₁＝a₁t

后半段有：v₂＝v₁－a₂t＝a₁t－3a₁t＝－2a₁t

可得：v₁∶v₂＝1∶2

 

25．一辆汽车从静止开始以匀加速度开出，然后保持匀速运动，最后匀减速运动，直到停止，下表给出了不同时刻汽车的速度，那么汽车从开出到开始做匀速运动经历的时间是______s。总共通过的路程是_______m。

时刻（s）	1.0	2.0	3.0	5.0	7.0	9.5	10.5
速度（m/s）	3	6	9	12	12	9	3

 

【答案】

4，96

 

26．甲的加速度为－5 m/s²，乙的加速度为3 m/s²，则以下说法中正确的是（    ）

（A）甲的加速度比乙大                   （B）甲向负方向运动

（C）甲比乙运动得快               （D）甲单位时间内速度的改变量比乙大

【答案】

D

 

27．将甲、乙两小球以大小相等的初速度抛出，甲球竖直上抛，乙球竖直下抛，则（    ）

（A）甲球落地时速度大于乙球落地时速度

（B）甲球落地所需时间等于乙球落地所需时间

（C）从抛出到落地的过程中，甲乙两球的平均速度相同

（D）运动过程中，任意时间内甲乙两球的速度变化量相同

【答案】

D

 

28．在空中某足够高处，以初速度20 m/s竖直上抛一物体，不计空气阻力，第1 s末到第5 s末物体通过的路程为（    ）

（A）40 m           （B）45 m            （C）50 m            （D）65 m

【答案】

C

 

29．如图所示，光滑斜面被等分成四段，AB＝BC＝CD＝DE，若一物体从A点由静止开始沿斜面向下运动，则（     ）

（A）物体通过AB、AC、AD、AE四段的时间之比为1∶\(\sqrt 2 \)∶\(\sqrt 3 \)∶2

（B）物体通过每一段的时间之比为2∶\(\sqrt 3 \)∶\(\sqrt 2 \)∶1

（C）物体通过每一段的平均速度之比为1∶\(\sqrt 2 \)∶\(\sqrt 3 \)∶2

（D）物体通过B、C、D、E四点的速度之比为1∶(\(\sqrt 2 \)＋1)∶(\(\sqrt 3 \)＋\(\sqrt 2 \))∶(2＋\(\sqrt 3 \))

【答案】

A

 

30．竖直上抛运动，上升和下落两次经过A点时间差为t₁，两次经过较高的B点时间差为t₂，求AB间的高度。

【答案】

\(\frac{1}{8}\)g(t₁²-t₂²)

【解析】

根据对称性可知，从最高点落至A、B点的时间分别为\(\frac{{{t_1}}}{2}\)、\(\frac{{{t_2}}}{2}\)，由自由落体规律可得：

h_AB＝\(\frac{1}{2}\)g(\(\frac{{{t_1}}}{2}\))²－\(\frac{1}{2}\)g(\(\frac{{{t_2}}}{2}\))²＝\(\frac{1}{8}\)g(t₁²-t₂²)。

 

31．甲、乙两车相距s₀＝40.5 m，同时沿平直公路做直线运动。甲车在前，以初速度v₁＝16 m/s、加速度为a₁＝－2 m/s²做匀减速直线运动；乙车在后，以初速度v₂＝4 m/s、加速度a₂＝1 m/s²与甲同向做匀加速直线运动，求：

（1）乙车追上甲车经历的时间；

（2）甲、乙两车相遇前相距的最大距离。

【答案】

（1）11 s

（2）64.5 m

【解析】

（1）乙车追上甲车时应满足：

s_乙＝s₀＋s_甲

有可能在追上前甲车停止运动（这就是在匀减速运动中常见的刹车陷阱），解题时可以设在追上前甲车已停止，则有：

v₂t＋\(\frac{1}{2}\)a₂t²＝s₀＋\(\frac{{v_1^2}}{{2{a_1}}}\)

4t＋0.5t²＝40.5＋64

t＝11 s

甲车停下所需的时间为＝8 s＜11 s，因此假设成立。

（2）两者在速度相同时相距最远，设用时t，有

v₁－a₁t＝v₂＋a₂t

16－2t＝4＋t

t＝4 s

Δs＝s_甲＋s₀－s_乙

＝（v₁t－\(\frac{1}{2}\)a₂t²）＋s₀－（v₂t＋\(\frac{1}{2}\)a₂t²）

＝(48＋40.5－24)m

＝64.5 m

 

32．古希腊哲学家亚里士多德认为重的物体比轻的物体坠落的快。意大利科学家伽利略对这个论断提出了质疑：

①根据这一论断，一块大石头比一块小石头的下落速度大；

②假定一块大石头下落速度为8个单位，一块小石头下落速度为4个单位；

③……

④由此从“重物比轻物落得快”的结论推出了相互矛盾的结果。

（1）请将伽利略的推理分析步骤③补充完整：

（2）请你设计一个简单的小实验，来证明实际生活中，重的物体并不一定比轻的物体下落的快。

【答案】

（1）当把两块石头捆在一起时，大石头会被小石头拖着而减慢，结果整个系统的下落速度应该小于8个单位；但两块石头捆在一起，总的重量比大石头还要重，因此整个系统下落的速度要比8个单位还大。

（2）略（合理即可，可引导学生综合运用控制变量等方法设计实验方案）

【解析】

无

 

33．如何利用所学的直线运动的知识，设计测量一口深井深度的方案。写出需要测量的物理量和校园查询的参数，并计算出井的深度。

【答案】

只要合理均可（样例：找一小石子从井口静止释放，用计时仪器测出从释放到听到石子下落到水面声音的时间间间隔t，查出声音在空气中的传播速度v_声，利用自由落体运动和匀速直线运动规律，即可计算出井的深度）