1．某单色光照射某金属时不能产生光电效应，则下述措施中可能使该金属产生光电效应的是（          ）

（A）延长光照时间                      （B）增大光的强度

（C）换用波长较短的光照射      （D）换用频率较低的光照射

【答案】

C

 

2．天然放射现象的发现揭示了（      ）

（A）原子不可再分              （B）原子的核式结构

（C）原子核还可再分          （D）原子核由质子和中子组成

【答案】

C

 

3．某交流发电机产生的感应电动势与时间的关系如图所。如果其他条件不变，仅使线圈的转速加倍，则交流电动势的最大值和周期分别变为（    ）

（A）400 伏，0.02 秒    （B）200 伏，0.02 秒

（C）400 伏，0.08 秒    （D）200 伏，0.08 秒

【答案】

B

 

4．某同学身高 1.8 m，在运动会上他参加跳高比赛，起跳后身体横着越过了 1.8 m 高度的横杆。据此可估算出他起跳时竖直向上的速度大约为（取 g ＝ 10 m/s²）（        ）

（A）2 m/s    （B）4 m/s    （C）6 m/s   （D）8 m/s

【答案】

B

【解析】

无

 

5．一列简谐横波向右传播，波速为 v。沿波传播方向上有相距为 L 的 P、Q 两质点，如图所示。某时刻 P、Q 两质点都处于平衡位置，且 P、Q 间仅有一个波峰。经过时间 t，Q 质点第一次运动到波谷。则 t 的可能值有（    ）

（A）1 个    （B）2 个    （C）3 个    （D）4 个

【答案】

D

【解析】

无

 

6．如图（a）所示，竖直放置的螺线管与导线abcd构成回路，导线所围区域内有一垂直纸面向里的变化的匀强磁场，螺线管下方水平桌面上有一导体圆环。导线abcd所围区域内磁场的磁感强度按图（b）中哪一图线所表示的方式随时间变化时，导体圆环将受到向上的磁场作用力？（              ）

【答案】

A

 

7．把太阳系各行星的运动近似看作匀速圆周运动，则离太阳越远的行星（      ）

（A）周期越小                      （B）线速度越小

（C）角速度越小                  （D）加速度越小

【答案】

BCD

 

8．一束复色可见光射到置于空气中的平板玻璃上，穿过玻璃后从下表面射出，变为 a、b 两束平行单色光，如图所示．对于两束单色光来说（        ）

（A）玻璃对 a 光的折射率较大

（B）a 光在玻璃中传播的速度较大

（C）b 光每个光子的能量较大

（D）b 光的波长较长

【答案】

AD

 

9．一定质量的理想气体自状态 A 经状态 C 变化到状态B这一过程在 V–T 图上表示如右图。则（         ）

（A）在过程 AC 中，外界对气体做功

（B）在过程 CB 中，外界对气体做功

（C）在过程 AC 中，气体压强不断变大

（D）在过程 CB 中，气体压强不断变小

【答案】

AC

 

10．图中 a、b 为竖直向上的电场线上的两点，一带电质点在 a 点由静止释放，沿电场线向上运动，到 b 点恰好速度为零．下列说法中正确的是（         ）

（A）带电质点在 a、b 两点所受的电场力都是竖直向上的

（B）a 点的电势比 b 点的电势高

（C）带电质点在 a 点的电势能比在 b 点的电势能小

（D）a 点的电场强度比 b 点的电场强度大

【答案】

ABD

 

11．如图所示，竖直光滑杆上套有一个小球和两根弹簧，两弹簧的一端各与小球相连，另一端分别用销钉 M、N 固定于杆上，小球处于静止状态.设拔去销钉 M 瞬间，小球加速度的大小为 12 米/秒²。若不拔去销钉 M 而拔去销钉 N 瞬间，小球的加速度可能是（取 g ＝ 10 米/秒²）（         ）

（A）22 米/秒²，竖直向上    （B）22 米/秒²，竖直向下

（C）2 米/秒²，竖直向上    （D）2 米/秒²，竖直向下

【答案】

BC

 

12．在倾角为 30° 的光滑斜面上垂直纸面放置一根长为 L，质量为 m 的直导体棒，一匀强磁场垂直于斜面向下，如图所示。当导体棒内通有垂直纸面向里的电流 I 时，导体棒恰好静止在斜面上，则磁感强度的大小为 B ＝______。

【答案】

$\frac{mg}{2IL}$

 

13．如图所示，质量不计的杆 O₁B 和 O₂A，长度均为 l，O₁ 和 O₂ 为光滑固定转轴，A 处有一凸起物搁在 O₁B 的中点，B 处用绳系在 O₂A 的中点，此时两短杆便组合成一根长杆。今在 O₁B 杆上的 C 点（C 为 AB 的中点）悬挂一重为 G 的物体，则 A 处受到的支承力大小为______，B 处绳的拉力大小为______。

【答案】

$\frac{G}{2}$，G

 

14．如图所示，古希腊某地理学家通过长期观测，发现 6 月 21 日正午时刻，在北半球 A 城阳光与铅直方向成 7.5° 角下射，而在 A 城正南方，与 A 城地面距离为 L 的 B 城，阳光恰好沿铅直方向下射，射到地球的太阳光可视为平行光。据此他估算出了地球的半径。试写出估算地球半径的表达式 R ＝______。

【答案】

$\frac{24L}{\pi }$

 

15．如图所示电路由 8 个不同的电阻组成，已知 R₁ ＝ 12 Ω，其余电阻阻值未知，测得 A、B 间的总电阻为 4 Ω。今将 R₁ 换成 6 Ω 的电阻，则 A、B 间的总电阻变为______ Ω。（提示：用等效替代法）

【答案】

3

 

16．天文观测表明，几乎所有远处的恒星（或星系）都在以各自的速度背离我们而运动，离我们越远的星体，背离我们运动的速度（称为退行速度）越大，也就是说，宇宙在膨胀，不同星体的退行速度 v 和它们离我们的距离 r 成正比，即

v ＝ Hr

式中 H 为一常量，称为哈勃常数，已由天文观察测定。为解释上述现象，有人提出一种理论，认为宇宙是从一个大爆炸的火球开始形成的。假设大爆炸后各星体即以不同的速度向外匀速运动，并设想我们就位于其中心，则速度越大的星体现在离我们越远。这一结果与上述天文观测一致。

由上述理论和天文观测结果，可估算宇宙年龄 T，其计算式为 T ＝________，根据近期观测，哈勃常数 H ＝ 3×10⁻² 米/秒·光年，其中光年是光在一年中行进的距离，由此估算宇宙的年龄约为_______年。

【答案】

$\frac{1}{H}$，1×10¹⁰

 

17．在做“用单摆测定重力加速度”的实验时，用摆长 l 和周期 T 计算重力加速度的公式是 g ＝______。如果已知摆球直径为 2.00 厘米，让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图（a）所示，那么单摆摆长是______。如果测定了 40 次全振动的时间如图（b）中秒表所示，那么秒表读数是_____秒，单摆的摆动周期是_______秒。

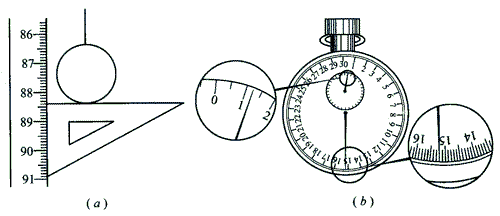
【答案】

$\frac{4{\pi }^{2}l}{T^2}$，0.8740 米或 87.40 厘米（0.874 米或 87.4 厘米不扣分），75.2，1.88

 

18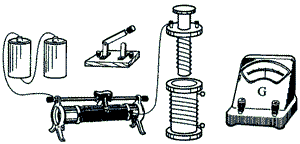．如图为“研究电磁感应现象”的实验装置。

（1）将图中所缺的导线补接完整。

（2）如果在闭合电键时发现灵敏电流计的指针向右偏了一下，那么合上电键后（         ）

 （A）将原线圈迅速插入副线圈时，电流计指针向右偏转一下

（B）将原线圈插入副线圈后，电流计指针一直偏在零点右侧

（C）原线圈插入副线圈后，将滑动变阻器触头迅速向左拉时，电流计指针向右偏转一下

（D）原线圈插入副线圈后，将滑动变阻器触头迅速向左拉时，电流计指针向左偏转一下

【答案】

（1）如图所示

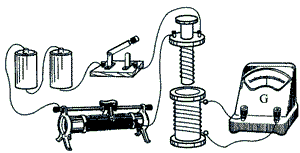
（2）A，D

 

19．某同学做“验证玻意耳定律”实验时，将注射器竖直放置，测得的数据如下表所示。发现第5组数据中的 pV 乘积值有较大偏差。如果读数和计算无误，那么造成此偏差的原因可能是_______或________。

实验次序	1	2	3	4	5
p（105 Pa）	1.21	1.06	0.93	0.80	0.66
V（mL）	33.2	37.8	43.8	50.4	69.2
pV（105 Pa·mL）	40.2	40.1	40.7	40.3	45.7

【答案】

温度升高，漏入气体

 

20．为了测定某辆轿车在平直路上起动时的加速度（轿车起动时的运动可近似看作匀加速运动），某人拍摄了一张在同一底片上多次曝光的照片（如图）。如果拍摄时每隔 2 s 曝光一次，轿车车身总长为 4.5 m，那么这辆轿车的加速度约为（         ）

（A）1 m/s²    （B）2 m/s²    （C）3 m/s²    （D）4 m/s²

【答案】

B

 

21．现有一阻值为 10.0 欧姆的定值电阻、一个电键、若干根导线和一个电压表，该电压表表面上有刻度但无刻度值，要求设计一个能测定某电源内阻的实验方案。（已知电压表内阻很大，电压表量程大于电源电动势，电源内阻约为几欧）要求：

（1）在右边方框中画出实验电路图。

（2）简要写出完成接线后的实验步骤。

（3）写出用测得的量计算电源内阻的表达式 r ＝__________。 

【答案】

（1）如图所示

（2）①断开电键，记下电压表偏转格数 N₁。

②合上电键，记下电压表偏转格数 N₂。

（3）r = $\frac{N_1-N_2}{N_2}$R

 

22．光线以入射角 i 从空气向折射率 n ＝ $\sqrt{2}$ 的透明媒质表面。

（1）当入射角 i ＝ 45° 时，求反射光线与折射光线间的夹角 θ。

（2）当入射角 i 为何值时，反射光线与折射光线间的夹角 θ ＝ 90°？

【答案】

（1）θ = 105°

（2）i = arctan$\sqrt{2}$

【解析】

（1）设折射角为 r，由折射定律

 $\frac{\sin i}{\sin r}$ = n                                  ①

sinr = $\frac{\sin i}{n}$ = 0.5

得 r = 30°                                ②

而 i′ = i = 45°                          ③

∴θ = 180° − 45° − 30° = 105°④

（2）此时 i′ + r = 90°⑤

sinr = cosi

代入折射定律 tan i = $\sqrt{2}$    ⑥

i = arctan$\sqrt{2}$                         ⑦

 

23．如图均匀薄壁 U 形管，左管上端封闭，右管开口且足够长。管的横截面积为 S，内装密度为 ρ 的液体。右管内有一质量为m的活塞搁在固定卡口上，卡口与左管上端等高，活塞与管壁间无摩擦且不漏气。温度为 T₀ 时，左、右管内液面高度相等，两管内空气柱长度均为 L，压强均为大气压强 p₀。现使两边温度同时逐渐升高，求：

（1）温度升高到多少时，右管活塞开始离开卡口上升？

（2）温度升高到多少时，左管内液面下降 h？

【答案】

（1）T₁ = （1 + $\frac{mg}{p_{0}S}$）T₀

（2）T₂ = $\frac{(p_0+\frac{mg}{S}+2\rho gh)(L+h)}{p_{0}L}$T₀

【解析】

（1）右管内气体为等容过程：$\frac{p_0}{T_0}$ = $\frac{p_1}{T_1}$                              ①

p₁ = p₀ + $\frac{mg}{S}$                                                    ②

由①、②式得 T₁ = （1 + $\frac{mg}{p_{0}S}$）T₀           ③

（2）对左管内气体列出状态方程 $\frac{p_{0}LS}{T_0}$ = $\frac{p_2{V}_2}{T_2}$               ④

p₂ = p₀ + $\frac{mg}{S}$ + 2ρgh                                                                 ⑤

V₂ = （L + h）S                                      ⑥

T₂ = $\frac{(p_0+\frac{mg}{S}+2\rho gh)(L+h)}{p_{0}L}$T₀       ⑦

 

24．如图所示，长为 L，电阻为 r ＝ 0.30 Ω、质量为 m ＝ 0.10 kg 的金属棒 CD 垂直跨搁在位于水平面上的两条平行光滑金属导轨上，两导轨间距也为 L，金属棒与导轨间接触良好，导轨电阻不计，导轨左端接有阻值 R ＝ 0.50 Ω 的电阻。量程为 0 ～ 3.0 A 的电流表串接在一条导轨上，量程为 0～ 1.0 V 的电压表接在电阻R的两端。垂直导轨平面的匀强磁场向下穿过平面。现以向右恒定外力 F 使金属棒向右移动。当金属棒以 v ＝2.0 m/s 的速度在导轨平面上匀速滑动时，观察到电路中的一个电表正好满偏，而另一个电表未满偏。问：

（1）此满偏的电表是什么表？说明理由。

（2）拉动金属棒的外力 F 多大？

（3）此时撤去外力 F，金属棒将逐渐慢下来，最终停止在导轨上。求从撤去外力到金属棒停止运动的过程中通过电阻 R 的电量。

【答案】

（1）电压表满偏。

理由是：若电流表满偏，回路中的电流应是 I ＝ 3.0 A，则电压表的示数应是 U ＝ IR ＝ 1.5 V 大于电压表量程；这不符合题意；若是电压表满偏，这时回路的电流是 I ＝ U/R ＝ 2.0 A，说明电流表未满偏。

（2）F ＝ 1.6 N

（3）q ＝ 0.25 C

【解析】

（1）电压表满偏。若电流表满偏，则 I = 3 A，U = IR = 1.5 V，大于电压表量程。

（2）由功能关系  Fv = I²（R+ r）                                               ①

而 I = $\frac{U}{R}$                                                                                            ②

F = $\frac{U^2(R+r)}{R^{2}v}$                                                                              ③

代入数据得 F = 1.6 N                                                                      ④

（3）由动量定量：mΔv = IBLΔt                                                   ⑤

两边求和：mΔv₁ + mΔv₂ + … = BLI₁Δt₁ + BLI₂Δt₂ +…           ⑥

即：mv = BLq                                                                                    ⑦

由电磁感应定律：E = BLv                                                             ⑧

E = I（R + r）                                                                                    ⑨

由⑦⑧⑨解得 q = $\frac{m{v}^2}{I(R+r)}$                                                       ⑩

代入数据得 q = 0.25 C                                                                    （11）

 

25．如图所示，一辆质量 m ＝ 2 千克的平板车左端放有质量 M ＝ 3 千克的小滑块，滑块与平板车之间的摩擦系数 μ ＝ 0.4。开始时平板车和滑块共同以 v₀ ＝ 2 米/秒的速度在光滑水平面上向右运动，并与竖直墙壁发生碰撞，设碰撞时间极短且碰撞后平板车速度大小保持不变，但方向与原来相反，平板车足够长，以至滑块不会滑到平板车右端。求：

（1）平板车第一次与墙壁碰撞后向左运动的最大距离。

（2）平板车第二次与墙壁碰撞前瞬间的速度 v。

（3）为使滑块始终不会滑到平板车右端，平板车至少多长？

【答案】

（1） s = 0.33 m

（2）v = 0.4 m/s

（3）l = 0.833 m

【解析】

（1）设第一次碰墙壁后，平板车向左移动 s，速度变为零。由于体系总动量向右，平板车速度为零时，滑块还在向右滑行。

由动能定理：

− μMgs = 0 − $\frac{1}{2}$mv₀²                              ①

s = $\frac{m{v}_0^2}{2\mu Mg}$                                                ②

代入数据得：s = 0.33 m                        ③

（2）假如平板车在第二次碰墙前还未和滑块相对静止，那么其速度的大小肯定还是 2 米/秒，滑块的速度则大于 2 米/秒，方向均向右，这样就违反动量守恒。所以平板车在第二次碰墙前肯定已和滑块具有共同速度 v，此即平板车碰墙前瞬间的速度。

Mv₀ − mv₀ =（M + m）v                        ④

v = $\frac{M-m}{M+m}$ v₀                                         ⑤

代入数据得：v = 0.4 m/s                       ⑥

（3）平板车与墙壁第一次碰撞后到滑块与平板车又达到共同速度 v 前的过程，可用图（a）（b）（c）表示，图（a）为平板车与墙碰撞后瞬间滑块与平板车的位置，图（b）为平板车到达最左端时两者的位置，图（c）为平板车与滑块再次达到共同速度时两者的位置。在此过程中滑块动能减少等于摩擦力对滑块所做功 μMgsʹ，平板车动能减少等于摩擦力对平板车所做 μMgsʺ（平板车从 B 到 A 再回到 B 的过程中摩擦力做功为零），其中 sʹ、sʺ 分别为滑块和平板车的位移。滑块和平板车动能总减少为 μMgl₁。其中 l₁ = sʹ + sʺ 为滑块相对平板车的位移。此后，平板车与墙壁发生多次碰撞，每次情况与此类似，最后停在墙边。设滑块相对平板车总位移为 l，则有：

$\frac{1}{2}$（M + m）v₀² = μMgl                 ⑦

l = $\frac{(M+m)v_0^2}{2\mu Mg}$                                ⑧

代入数据得 l = 0.833 m                ⑨

l 即为平板车的最短长度。