1．在探究小车速度随时间变化的规律的实验中，用打点计时器在纸带上打的点记录了小车的运动情况。某同学做此实验时的步骤如下：

（A）拉住纸带，将小车移至靠近打点计时器处，放开纸带，再接通电源；

（B）将打点计时器固定在长木板上，并接好电路；

（C）把一条细绳拴在小车上，细绳跨过定滑轮，下面挂上适当的钩码；

（D）小车停止运动后，直接取下纸带；

（E）将纸带固定在小车尾部，并穿过打点计时器的限位孔；

（F）换上新纸带，再重复操作两次，然后从各纸带中选取一条点迹清晰的进行数据处理。

其中错误或遗漏的步骤有：

（1）________；（2）________。

将以上步骤完善后，其合理的顺序为________。

【答案】

（1）A中应先接通电源，再放开纸带

（2）D中取纸带前应先断开电源

BECADF

【解析】

实验过程中应先接通电源，再放开纸带；取纸带前应先断开电源，所以错误的步骤是A、D。该实验步骤中合理的顺序为BECADF。

 

2．在“探究小车速度随时间变化的规律”实验中，如图所示为记录小车运动情况的一条纸带，图中A、B、C、D、E为相邻的计数点，相邻计数点间的时间间隔T＝0.1 s。

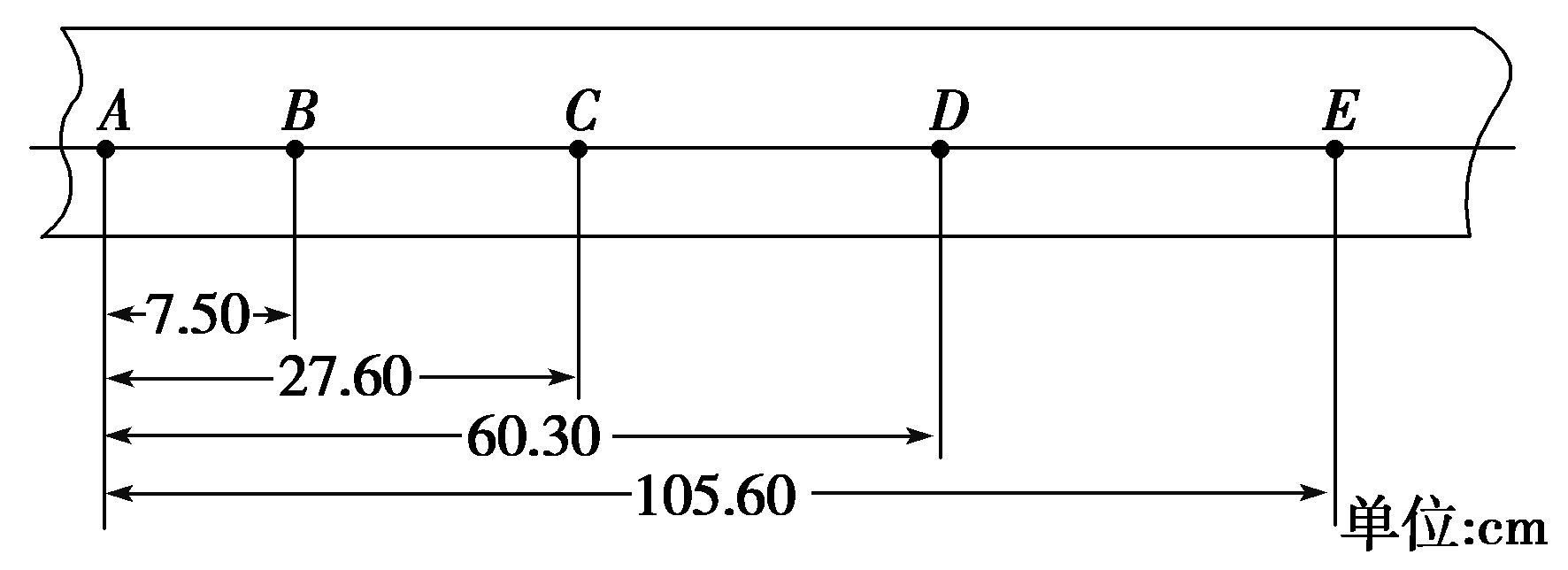
（1）计算D、C、B各点的瞬时速度，v_D＝________m/s，v_C＝________m/s，v_B＝________m/s.

（2）在如图所示坐标系中作出小车的v-t图象，并根据图象求出a＝________。

【答案】

（1）3.90，2.64，1.38

（2）如图，12.6 m/s²

【解析】

（1）若时间较短，用平均速度可以代替某点的瞬时速度

D点的瞬时速度v_D＝3.90 m/s，

C点的瞬时速度v_C＝2.64 m/s，

B点的瞬时速度v_B＝1.38 m/s。

（2）由（1）中数据作出小车的v-t图象如图所示，由图线的斜率可求得它的平均加速度

a＝\(\frac{{\Delta v}}{{\Delta t}}\)＝\(\frac{{1.26}}{{0.1}}\) m/s²＝12.6 m/s²

 

3．在“探究小车速度随时间变化规律”的实验中，下列说法中正确的是（    ）

（A）长木板一定要水平摆放

（B）使用刻度尺测量长度时，不必估读

（C）使用刻度尺测量长度时，要估读到最小刻度的下一位

（D）作v－t图象时，所描线必须经过每一个点

【答案】

C

【解析】

实验过程中，一般长木板应平放，不能侧向倾斜，但适当一端高一端低，也是可以的，A错误。使用刻度尺测长度时，需要估读，B错误、C正确。作v-t图象时，若各点与直线拟合，则作直线并使直线经过尽量多的点，D错误。

 

4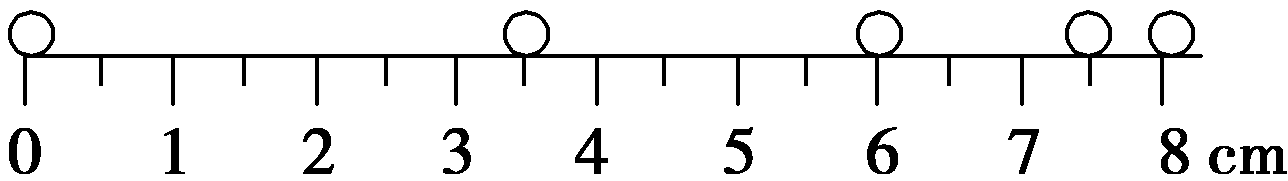．一小球在水平桌面上做直线运动，用照相机对着小球每隔0.1 s拍照一次，得到一幅频闪照片，用刻度尺量得照片上小球各位置如图所示，已知照片与实物的比例为1∶10，则（    ）

（A）图中对应的小球在通过8 cm距离内的平均速度是2 m/s

（B）图中对应的小球在通过8 cm距离内的平均速度是1.6 m/s

（C）图中对应的小球通过6 cm处的瞬时速度是2.5 m/s

（D）图中对应的小球通过6 cm处的瞬时速度是2 m/s

【答案】

AD

 

5．在“探究小车速度随时间变化规律”实验中，下列方法中有助于减小实验误差的是（     ）

（A）选取计数点，把每打5个点的时间间隔作为一个时间单位

（B）使小车运动的加速度尽量小些

（C）舍去纸带上开始时密集的点，只利用点迹清晰、点间间隔适当的那一部分进行测量、计算

（D）适当增加挂在细绳下钩码的个数

【答案】

ACD

【解析】

选取计数点可以使相邻点间的间隔增大，在用直尺测量这些点间的间隔时，在一次测量绝对误差基本相同的情况下，相对误差较小，因此选项A正确。在实验中如果小车运动的加速度过小，打出的点子就很密，长度测量的相对误差较大，测量的准确度会降低，因此小车运动的加速度适当大一些较好。如果小车的加速度控制较好，以能在50 cm长的纸带上清楚地取出7～8个计数点为宜，所以选项B是错误的。若适当增加挂在细绳下钩码的个数，意味着适当增大小车运动的加速度，所以选项D正确。为了减小长度测量的相对误差，舍去纸带上过于密集，甚至分辨不清的点是必要的，因此选项C正确。

 

6．一小球在桌面上从静止开始做加速直线运动，现用高速摄影机在同一底片上多次曝光，记录下小球每次曝光的位置，并将小球的位置编号。如图甲所示，1位置恰为小球刚开始运动的瞬间，作为零时刻．摄影机连续两次曝光的时间间隔均相同，小球从1位置到6位置的运动过程中经过各位置的速度分别为v₁＝0，v₂＝0.06 m/s，v₃＝__________m/s，v₄＝0.18 m/s，v₅＝__________m/s。在图乙所示的坐标纸上作出小球的速度-时间图象（保留描点痕迹）。

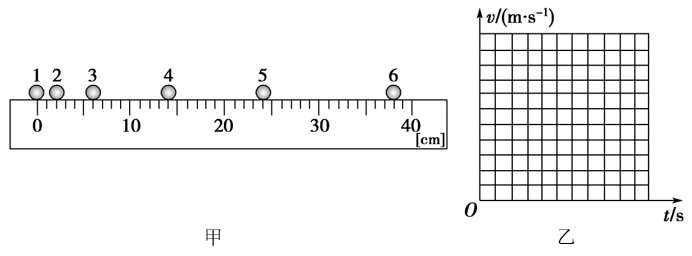
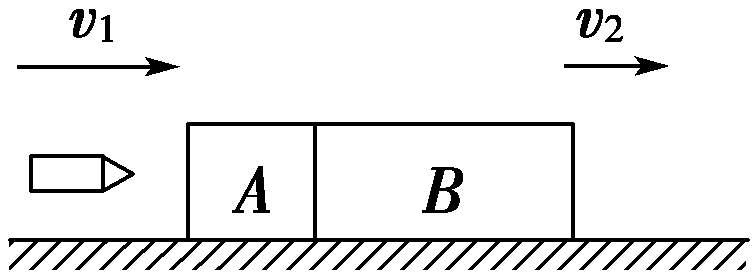
【答案】

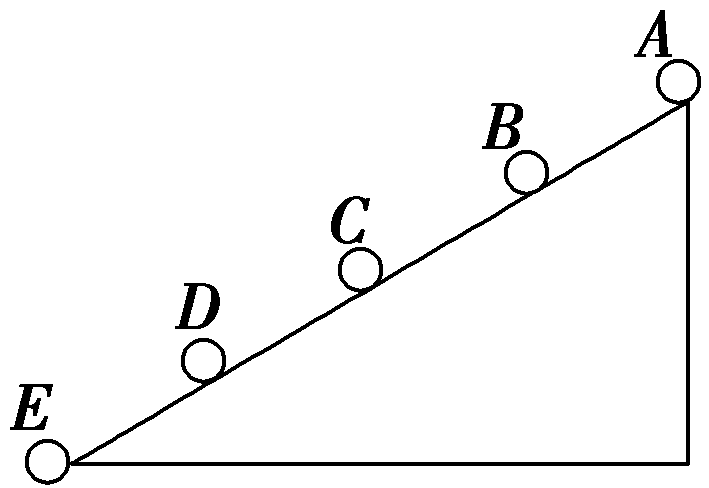
一小球在桌面上从静止开始做加速直线运动，现用高速摄影机在同一底片上多次曝光，记录下小球每次曝光的位置，并将小球的位置编号。如图甲所示，1位置恰为小球刚开始运动的瞬间，作为零时刻．摄影机连续两次曝光的时间间隔均相同，小球从1位置到6位置的运动过程中经过各位置的速度分别为v₁＝0，v₂＝0.06 m/s，v₃＝__________m/s，v₄＝0.18 m/s，v₅＝__________m/s。在图乙所示的坐标纸上作出小球的速度-时间图象（保留描点痕迹）。

 

7．如图所示，用滴水计时器研究小车的速度随时间的变化，步骤如下 ：

（1）在斜面上铺上白纸，用图钉钉住．把滴水计时器固定在小车的一端（也可固定在侧面），在小车的另一端（或另一侧）固定一个平衡物，如图。调节滴水计时器滴水速度，使之每秒滴n滴（以滴水计时器内盛满水时为准）。在斜面顶端放置一浅盘。

（2）把小车放在斜面顶端，把调好的滴水计时器盛满水，使水滴能滴入浅盘。随即在撤去浅盘的同时________，于是水滴在白纸上留下描述小车运动规律的点迹。小车到达斜面末端时立即将它握住并移开。

（3）取下白纸，用直尺测量连续相邻各点迹的中心之间的距离x₁，x₂，…，x_n，x_n＋1，…则第n点对应的速度v_n＝________。

【答案】

（2）放开小车

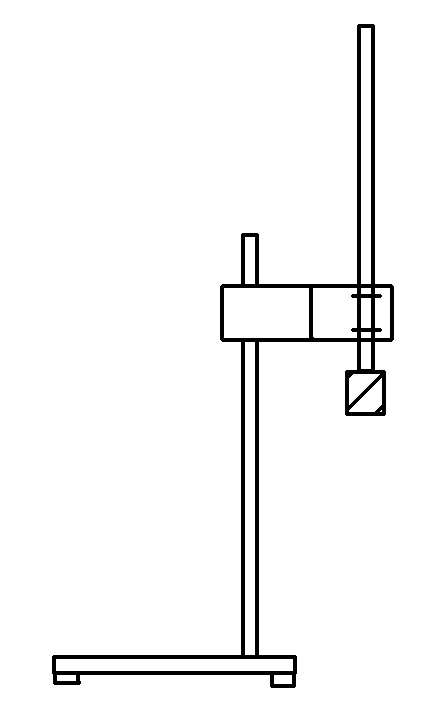
（3）\(\frac{{n({x_n} + {x_{n + 1}})}}{2}\)

 

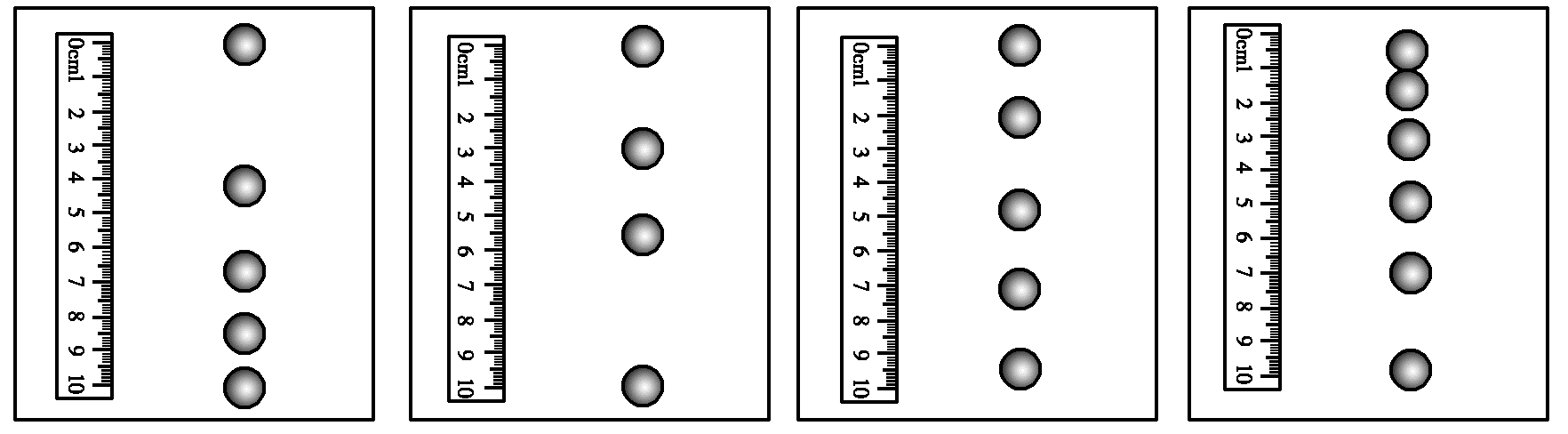
8．如图甲所示，用打点计时器记录小车的运动情况．小车开始在水平玻璃板上运动，后来在薄布面上做减速运动。所打出的纸带及相邻两点间的距离（单位：cm）如图乙所示，纸带上相邻两点间对应的时间间隔为0.02 s。试用作图法（v-t图象）求出小车在玻璃板上的运动速度。

【答案】

0.85 m/s

【解析】

设对应点1、2、3、4、5的瞬时速度分别为v₁、v₂、v₃、v₄、v₅，则有

v₁＝75 cm/s＝0.75 m/s，

v₂＝65 cm/s＝0.65 m/s，

v₃＝55 cm/s＝0.55 m/s，

v₄＝45 cm/s＝0.45 m/s，

v₅＝35 cm/s＝0.35 m/s，

以速度为纵坐标，以时间为横坐标建立直角坐标系．用描点法作出小车在薄布上做减速运动时的v-t图象．将图象延长，使其与纵轴相交，如图所示。由图象可知，小车做减速运动的初速度为0.85 m/s，即为小车在玻璃板上的运动速度。

 

9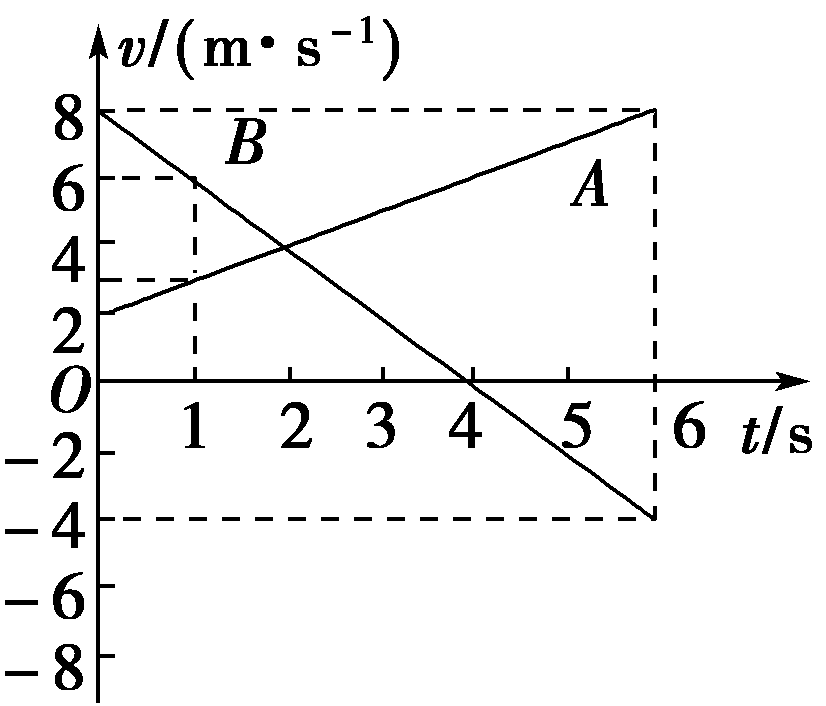．如图为A、B两个物体做匀变速直线运动的v-t图象。

（1）A、B各做什么运动？求其加速度；

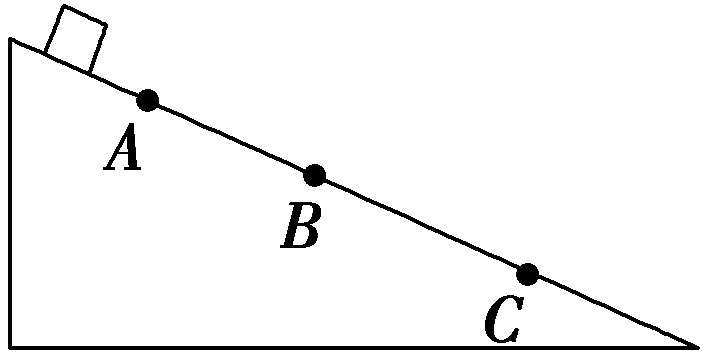
（2）两图线的交点的意义是什么？

（3）求1 s末A、B的速度；

（4）求6 s末A、B的速度。

【答案】

（1）A物体沿规定的正方向做匀加速直线运动，加速度的大小a₁＝1 m/s²，加速度的方向沿规定的正方向；B物体前4 s沿规定的正方向做匀减速直线运动，4 s后沿反方向做匀加速直线运动，加速度的大小a₂＝2 m/s²，加速度的方向与规定的正方向相反。

（2）两图线的交点表示此时刻两个物体的速度相同。

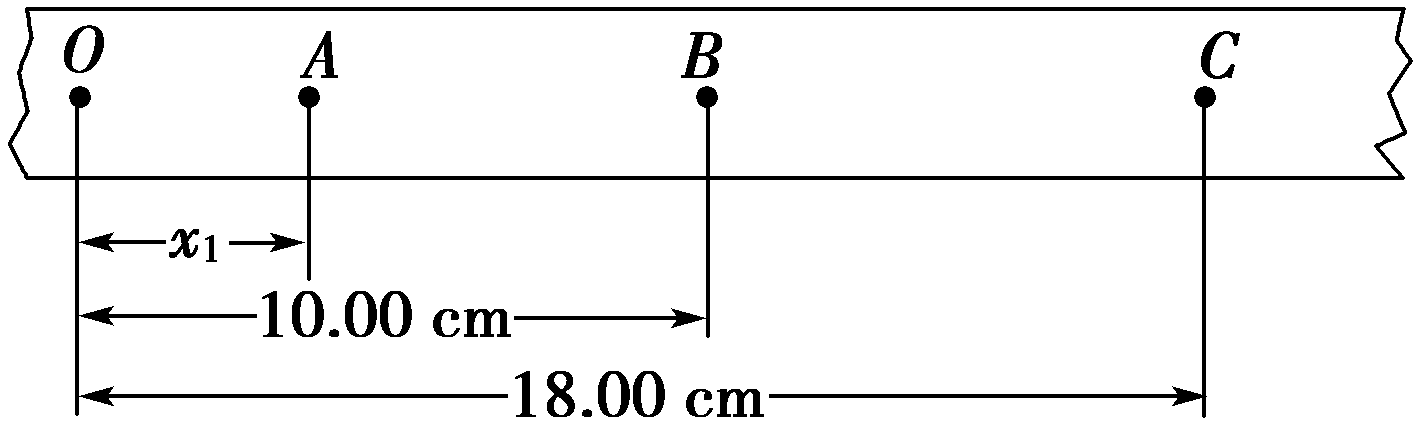
（3）1 s末A物体的速度大小为3 m/s，方向与规定的正方向相同；B物体的速度大小为6 m/s，方向与规定的正方向相同。

（4）6 s末A物体的速度大小为8 m/s，方向与规定的正方向相同；B物体的速度大小为4 m/s，方向与规定的正方向相反。

 

10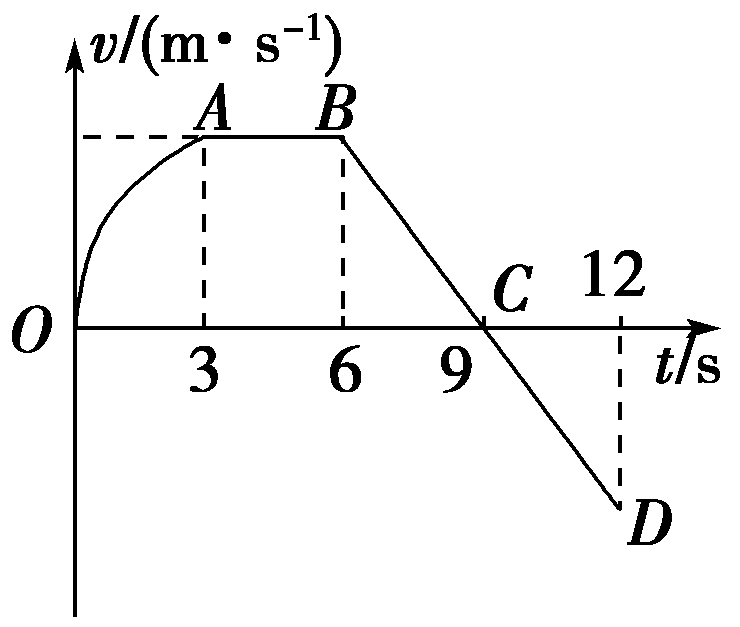．一个沿直线运动的物体的v-t图象如图所示，则下列分析错误的是（    ）

（A）图象OA段表示物体做非匀变速运动，AB段表示物体静止

（B）图象AB段表示物体做匀速直线运动

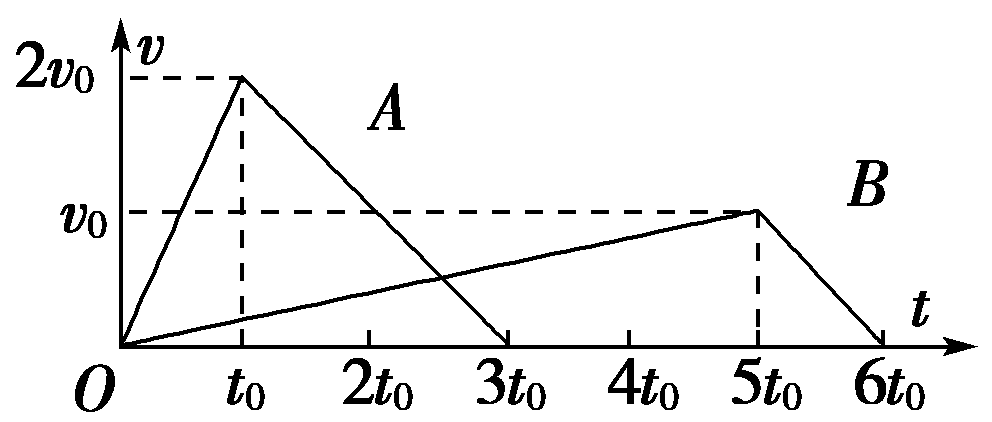
（C）在0～9 s内物体的运动方向相同

（D）在9～12 s内物体的运动方向与0～9 s内的运动方向相反

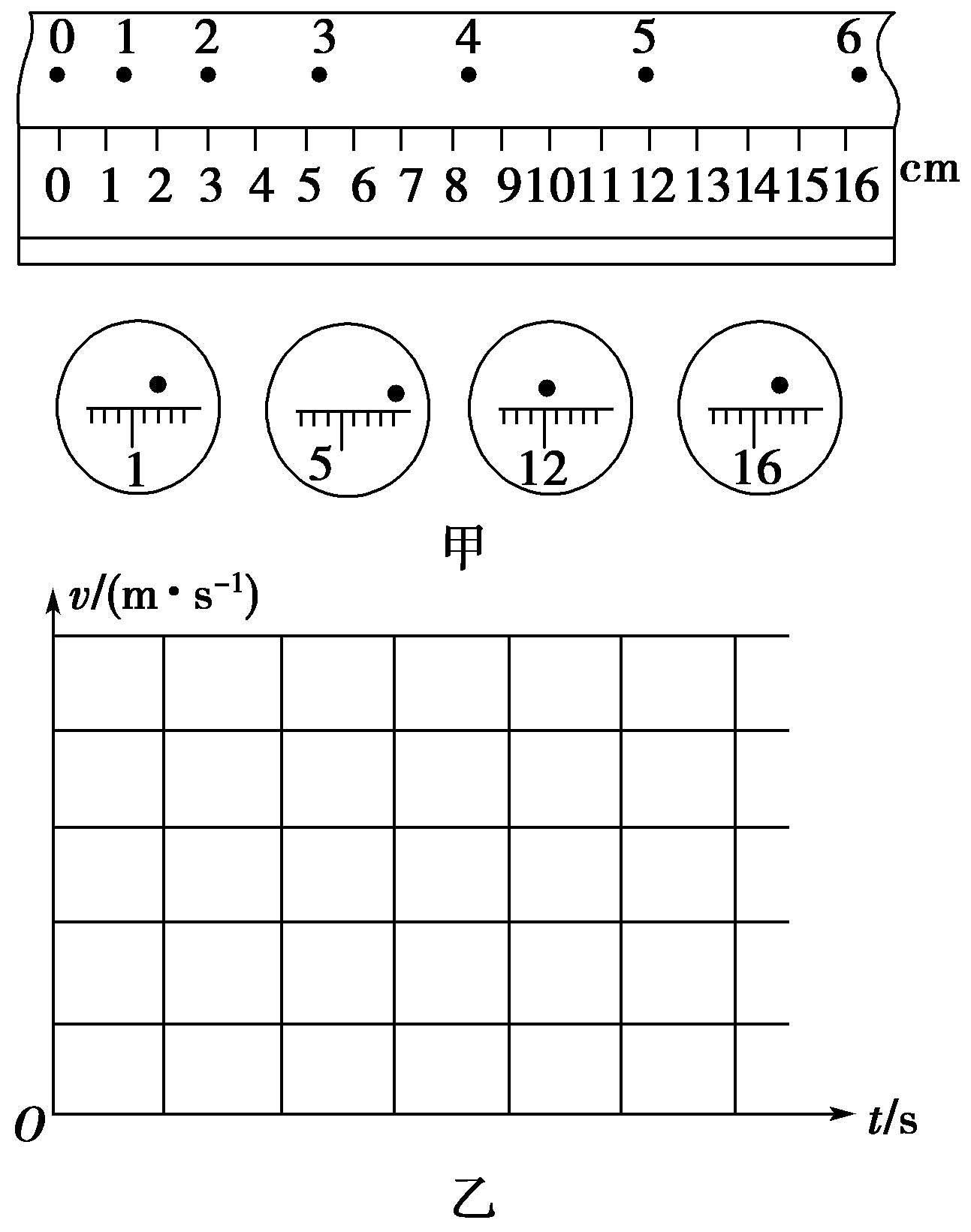
【答案】

A

【解析】

v-t图象是曲线，表示物体做非匀变速直线运动，图象与t轴平行表示物体做匀速直线运动，图象是倾斜直线表示物体做匀变速直线运动，A错误，B正确；0～9 s速度始终为正值，说明速度方向不变，C正确；9～12 s速度为负值，说明速度方向与正方向相反，D正确。

 

11．A、B两个物体在同一直线上做匀变速直线运动，它们的速度图象如图所示，则以下说法正确的是（    ）

（A）A、B两物体运动方向一定相反

（B）A、B两物体的加速度方向相同

（C）t＝4 s时，A、B两物体的速度相同

（D）A物体的加速度比B物体的加速度大

【答案】

C

【解析】

A、B两物体都向正方向运动，运动方向相同，A错；又因A加速运动，B减速运动，故A、B的加速度方向相反，B错；t＝4 s时，两物体的速度相同，C对；两物体的v-t图象，B的斜率较大，即B物体的加速度较大，D错。

 

12．一物体从静止开始以2 m/s²的加速度做匀加速直线运动，经5 s后做匀速直线运动，最后2 s的时间内物体做匀减速直线运动直至静止。求：

（1）物体做匀速直线运动的速度是多大？

（2）物体做匀减速直线运动时的加速度是多大？

【答案】

（1）10 m/s

（2）5 m/s²，方向与速度方向相反

【解析】

解题关键是画出如下的示意图：

设图中A→B为匀加速直线运动，B→C为匀速直线运动，C→D为匀减速直线运动，匀速运动段的速度为AB段的末速度，也为CD段的初速度

（1）由速度、时间的关系式得

v_B＝a₁t₁＝2×5 m/s＝10 m/s，

即做匀速直线运动的速度为10 m/s

v_C＝v_B＝10 m/s

（2）由v＝v₀＋a₂t₂得

a₂＝\(\frac{{{v_D} - {v_C}}}{{{t_2}}}\)＝\(\frac{{0 - 12}}{2}\) m/s²＝－5 m/s²

负号表示加速度方向与v_B方向相反

 

13．一辆匀加速行驶的汽车，经过路旁两根电线杆共用5 s时间，汽车的加速度为2 m/s²，它经过第2根电线杆时的速度为15 m/s，则汽车经过第1根电线杆的速度为（    ）

（A）2 m/s           （B）10 m/s         （C）2.5 m/s         （D）5 m/s

【答案】

D

【解析】

由题意知v＝15 m/s，a＝2 m/s²，t＝5 s，根据v＝v₀＋at得，v₀＝v－at＝15 m/s－2×5 m/s＝5 m/s，故选D。

 

14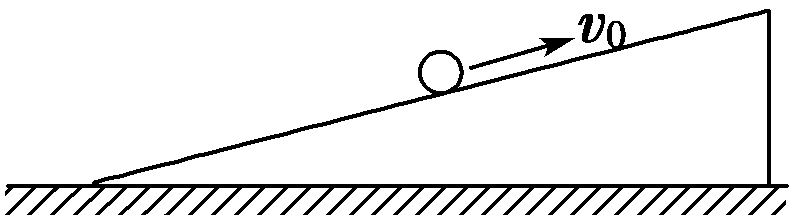．如图所示，小球以v₀＝6 m/s的速度从中间滑上足够长的光滑斜面。已知小球在斜面上运动时的加速度大小为2 m/s²，问小球速度大小为3 m/s时需多长时间？（小球在光滑斜面上运动时，加速度的大小和方向均不变 ）

【答案】

1.5 s或4.5 s

【解析】

（1）当小球在上升过程中速度减为3 m/s时，以沿斜面向上的方向为正方向，此时，v₀＝6 m/s，v＝3 m/s，a＝－2 m/s²，

根据v＝v₀＋at得t₁＝\(\frac{{v - {v_0}}}{a}\)＝\(\frac{{3 - 6}}{{ - 2}}\) s＝1.5 s

（2）当小球在下滑过程中，速度达3 m/s，以沿斜面向上的方向为正方向，则v₀＝6 m/s，v＝－3 m/s，a＝－2 m/s²，

由v＝v₀＋at得：t₂＝\(\frac{{v - {v_0}}}{a}\)＝\(\frac{{-3 - 6}}{{ - 2}}\) s＝4.5 s

 

15．在平直公路上，一辆汽车以108 km/h的速度行驶，司机发现前方有危险立即刹车，刹车时加速度大小为6 m/s²，求：

（1）刹车后3 s末汽车的速度大小；

（2）刹车后6 s末汽车的速度大小。

【答案】

（1）12 m/s

（2）0

【解析】

v₀＝108 km/h＝30 m/s，规定v₀的方向为正方向，则a＝－6 m/s²，汽车刹车所用的总时间t₀＝\(\frac{{0 - {v_0}}}{a}\)＝\(\frac{{0 - 30}}{{ - 6}}\)＝5 s

（1）t₁＝3 s时的速度v₁＝v₀＋at＝30 m/s－6×3 m/s＝12 m/s

（2）由于t₀＝5 s＜t₂＝6 s，故6 s末时汽车已停止，即v₂＝0

 

16．一汽车在平直的公路上以20 m/s的速度匀速行驶，前面有情况需紧急刹车，刹车的加速度大小是8 m/s²，刹车后可视为匀减速直线运动，求刹车3 s后汽车的速度。

【答案】

0

【解析】

设汽车从开始刹车到速度为零所用的时间为t，取汽车运动的方向为正方向。

由v＝v₀＋at，得t＝\(\frac{{v - {v_0}}}{a}\)＝\(\frac{{0 - 20}}{{ - 8}}\) s＝2.5 s，汽车在2.5 s末速度减为零而停下，汽车不再运动，所以3 s后汽车的速度为零。

 

17．下列有关匀变速直线运动的认识，其中正确的是（     ）

（A）物体在一条直线上运动，若在相等的时间内通过的位移相等，则物体的运动就是匀变速直线运动

（B）加速度大小不变的运动就是匀变速直线运动

（C）匀变速直线运动是速度变化量为零的运动

（D）匀变速直线运动的加速度是一个恒量

【答案】

D

【解析】

匀变速直线运动有两个特点：（1）轨迹为直线．（2）加速度恒定．只有具备这两个特点，物体做的才是匀变速直线运动．B错、D对。匀变速直线运动的速度不断变化，所以速度变化量不为零，相等时间内通过的位移也不相同，A、C错误。

 

18．某物体做匀变速直线运动，在运用公式v＝v₀＋at解题时，若取初速度方向为正方向，则下列说法正确的是（    ）

（A）匀加速直线运动中，加速度a取负值

（B）匀加速直线运动中，加速度a取正值

（C）匀减速直线运动中，加速度a取负值

（D）无论匀加速直线运动还是匀减速直线运动，加速度a均取正值

【答案】

BC

【解析】

物体做匀加速直线运动，速度方向与加速度方向相同，由于初速度为正值，故加速度也应取正值，A错，B对；匀减速直线运动中加速度方向与速度方向相反，加速度应取负值，C对、D错。

 

19．一小球在斜面上由静止开始匀加速滚下，进入水平面后又做匀减速运动，直至停止。如图所示的v-t图象中可以反映小球这一运动过程的是（     ）

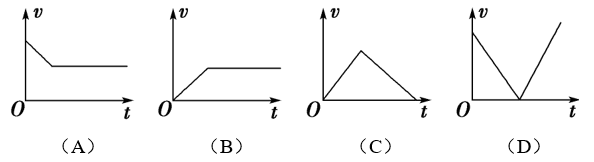
【答案】

C

 

20．星级快车出站时能在150 s内匀加速到180 km/h，然后正常行驶。某次因意外列车以加速时的加速度大小将车速减至108 km/h。以初速度方向为正方向，则下列说法错误的是（    ）

（A）列车加速时的加速度大小为\(\frac{1}{3}\) m/s²

（B）列车减速时，若运用v＝v₀＋at计算瞬时速度，其中a＝－\(\frac{1}{3}\) m/s²

（C）若用v－t图象描述列车的运动，减速时的图线在时间轴t轴的下方

（D）列车由静止加速，1 min内速度可达20 m/s

【答案】

C

【解析】

列车的加速度大小a＝\(\frac{{\Delta v}}{{\Delta t}}\)＝\(\frac{1}{3}\) m/s²＝\(\frac{1}{3}\) m/s²，减速时，加速度方向与速度方向相反，aʹ＝－\(\frac{1}{3}\) m/s²，故A、B两项都正确．列车减速时，v-t图象中图线依然在时间轴t轴的上方，C项错．由v＝at可得v＝\(\frac{1}{3}\)×60 m/s＝20 m/s，D项对。

 

21．甲、乙、丙三个物体均做匀变速运动，通过A点时，物体甲的速度是6 m/s，加速度是1 m/s²；物体乙的速度是2 m/s，加速度是6 m/s²；物体丙的速度是－4 m/s，加速度是2 m/s²。则下列说法中正确的是（     ）

（A）通过A点时，物体甲最快，乙最慢

（B）通过A点前1 s时，物体丙最快，乙最慢

（C）通过A点后1 s时，物体乙最快，丙最慢

（D）通过A点时，物体甲最快，丙最慢

【答案】

ABC

【解析】

物体丙的速度是－4 m/s的含义是速度大小为4 m/s，负号表示其速度方向与所选定的正方向相反，不表示大小。过A点时，速度大小满足的关系为v_甲>v_丙>v_乙，故A说法是正确的，D说法错误．由v＝v₀＋at知过A点前1 s时，v_甲＝5 m/s，v_乙＝－4 m/s，v_丙＝－6 m/s，则速度大小满足的关系为v_丙>v_甲>v_乙，故B说法正确．过A点1 s后，v_甲＝7 m/s，v_乙＝8 m/s，v_丙＝－2 m/s，则有速度大小满足的关系为v_乙>v_甲>v_丙，故C说法正确。

 

22．一个做初速度为零的匀加速直线运动的物体，它在第1 s末，第2 s末，第3 s末的瞬时速度之比是（    ）

（A）1∶1∶1             （B）1∶2∶3              （C）1²∶2²∶3²          （D）1∶3∶5

【答案】

B

【解析】

由v＝at得v₁∶v₂∶v₃＝at₁∶at₂∶at₃＝1∶2∶3，故选项B正确。

 

23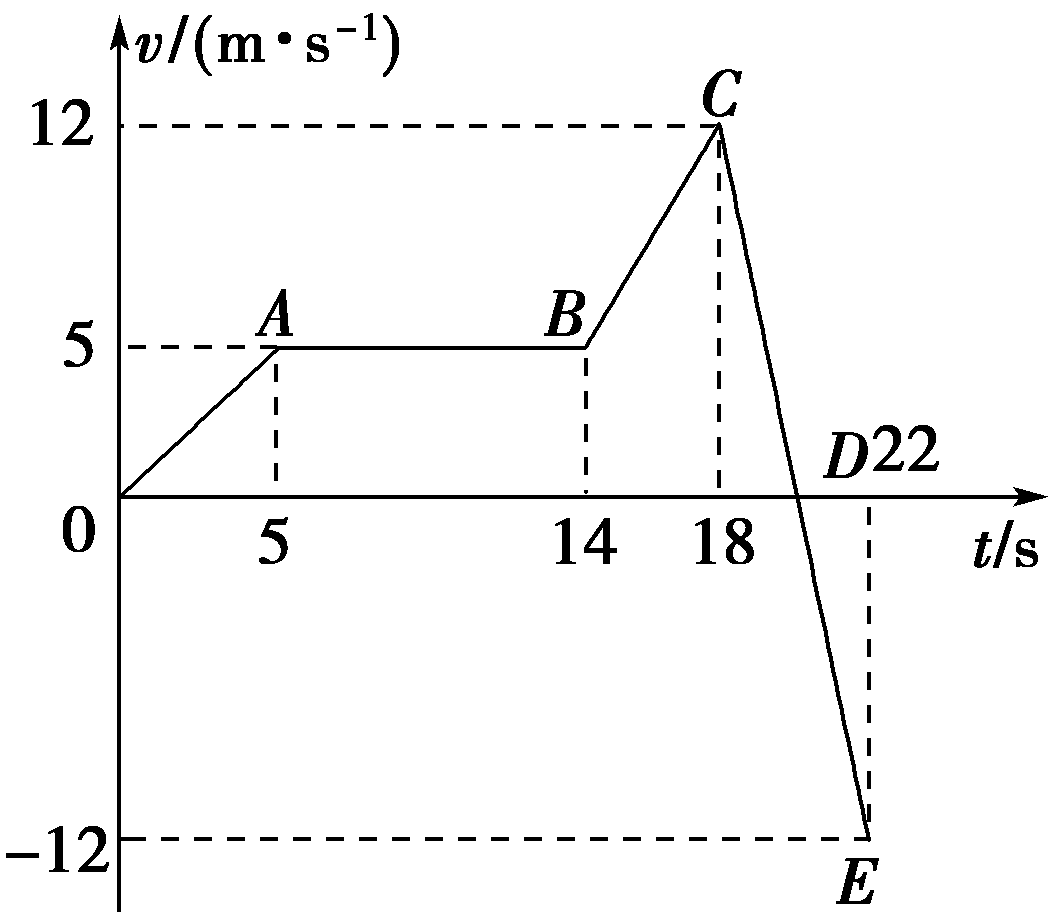．如图所示，为一质点在0～22 s时间内做直线运动的v-t图象，则下列说法中正确的是（    ）

（A）CD段和DE段的加速度方向相同

（B）整个过程中，BC段的加速度最大

（C）整个过程中，C点离出发点最远

（D）DE段质点做匀加速直线运动

【答案】

AD

【解析】

由图知CE段的加速度相同，A正确；整个过程中，CE段的加速度最大，D点时离出发点最远，所以B、C选项均错；DE段质点速度随时间的增加而均匀增大，质点做匀加速直线运动，D正确。

 

24．磁悬浮列车由静止开始加速出站，加速度为0.6 m/s²，2 min后列车速度为多大？列车匀速运动时速度为432 km/h，如果以0.8 m/s²的加速度减速进站，求减速160 s时速度为多大？

【答案】

72 m/s，0

【解析】

取列车开始运动方向为正方向．列车初速度v₁₀＝0，则列车2 min后的速度v＝v₁₀＋a₁t₁＝（0＋0.6×2×60）m/s＝72 m/s

当列车减速进站时a₂＝－0.8 m/s²

初速度v₂₀＝432 km/h＝120 m/s

从刹车到速度为0的时间t₀＝\(\frac{{ - {v_{20}}}}{{{a_2}}}\)＝\(\frac{{ - 120}}{{ - 0.8}}\) s＝150 s

所以160 s时列车已经停止运动，速度为0

 

25．试说明如图所示的图象中物体的运动情况。

【答案】

图甲中，物体运动的加速度越来越大，速度越来越大，表示物体做加速度越来越大的变加速直线运动。

图乙中，物体运动的加速度越来越小，最后为0，速度越来越大，最后不变，表示物体做加速度越来越小的变加速直线运动，直到加速度为0，做匀速直线运动。

图丙中，物体运动的加速度越来越大，速度越来越小，最后为0，表示物体做加速度越来越大的变减速直线运动，直到速度减为0。

图丁中，物体运动的加速度越来越小，速度越来越小，表示物体做加速度越来越小的变减速直线运动。

 

26．高空侦察机可进行高空侦察，导弹则是打击高空侦察机的有力武器．假设某日有一架高空侦察机正以300 m/s的速度向某城市飞来，它通过该城市上空的A点。某导弹基地通过雷达探测并计算高空侦察机的飞行规律，在高空侦察机离A点尚有一段距离时发射导弹，导弹以80 m/s²的加速度做匀加速直线运动，以1 200 m/s的速度在A点击中敌机，求 ：

（1）导弹发射后经过多长时间击中敌机？

（2）敌机离A点多远时，开始发射导弹？

【答案】

（1）15 s

（2）4.5 km

【解析】

（1）导弹由静止做匀加速直线运动，v₀＝0，

据公式v＝v₀＋at有：

t＝\(\frac{v}{a}\)＝\(\frac{{1200}}{{80}}\) s＝15 s，

即导弹发射后经15 s时间击中敌机。

（2）敌机做匀速直线运动，15 s通过的位移

x＝vʹt＝300×15 m＝4 500 m＝4.5 km，

即当敌机离A点4.5 km时，开始发射导弹。

 

27．卡车原来以 10 m/s 的速度匀速在平直的公路上行驶，因为路口出现红灯，司机从较远的地方即开始刹车，使卡车匀减速前进。当车减速到 2 m/s时，交通灯变为绿灯，司机立即放开刹车，并且只用了减速过程的一半时间卡车就加速到原来的速度，从刹车开始到恢复原来的速度共用了 12 s。求：

（1）减速与加速过程中的加速度；

（2）开始刹车后 2 s 末及 10 s 末的瞬时速度。

【答案】

（1）－1 m/s²，2 m/s²

（2）8 m/s，6 m/s

【解析】

（1）卡车先做匀减速运动，再做匀加速运动，其运动简图如图所示。设卡车从A点开始减速，则 v_A ＝ 10 m/s，用 t₁ 时间到达 B 点，从 B 点又开始加速经过时间 t₂ 到达 C 点，则

v_B＝2 m/s，v_C＝10 m/s，且 t₂＝\(\frac{{{t_1}}}{2}\)，

t₁ ＋ t₂ ＝ 12 s．可得 t₁ ＝ 8 s，t₂ ＝ 4 s，由 v ＝ v₀ ＋ at 得，

在AB段 v_B＝v_A＋a₁t₁，①

在 BC 段 v_C＝v_B＋a₂t₂，②

联立①②两式，代入数据得

a₁＝－1 m/s²，a₂＝2 m/s²

（2）开始刹车后 2 s 末的速度为 v₁＝v_A＋a₁t＝ 10 m/s－1×2 m/s ＝ 8 m/s

10 s 末的速度为 v₂＝v_B＋a₂t＝2 m/s＋2×2 m/s＝6 m/s

 

28．飞机着陆后做匀减速滑行，着陆时的初速度是216 km/h，在最初2 s内滑行114 m。求：

（1）5 s末的速度大小是多少？

（2）飞机着陆后12 s内滑行多远？

【答案】

（1）45 m/s

（2）504 m

【解析】

（1）最初2 s内：

x₁＝v₀t＋\(\frac{1}{2}\)at²，

解得：a＝－3 m/s²，

5 s末的速度：v₂＝v₀＋at＝45 m/s.

（2）着陆减速总时间：t＝\(\frac{{\Delta v}}{a}\)＝20 s，

飞机着陆后12 s内的位移：

x₂＝v₀t＋\(\frac{1}{2}\)at²＝504 m

 

29．某质点做直线运动的位移随时间变化的关系是x＝4t＋2t²，x与t的单位分别为m和s，则质点的初速度与加速度分别为（     ）

（A）4 m/s与2 m/s²                  （B）0与4 m/s²

（C）4 m/s与4 m/s²                 （D）4 m/s与0

【答案】

C

【解析】

对比x＝4t＋2t²和位移公式x＝v₀t＋\(\frac{1}{2}\)at²，可知其初速度v₀＝4 m/s，2＝\(\frac{1}{2}\)a，则加速度a＝4 m/s²。

 

30．一物体做匀减速直线运动，初速度大小为v₀＝5 m/s，加速度大小为a＝0.5 m/s²，求：

（1）物体在3 s内的位移大小；

（2）物体在第3 s内的位移大小。

【答案】

（1）12.75 m

（2）3.75 m

【解析】

（1）用位移公式求解，3 s内物体的位移：

x₃＝v₀t₃＋\(\frac{1}{2}\)（－a）t₃²＝5×3 m－\(\frac{1}{2}\)×0.5×3² m＝12.75 m

（2）同理2 s内物体的位移：

x₂＝v₀t₂＋\(\frac{1}{2}\)（－a）t2²＝5×2 m－\(\frac{1}{2}\)×0.5×2² m＝9 m

因此，第3 s内的位移：

x＝x₃－x₂＝12.75 m－9 m

＝3.75 m

 

31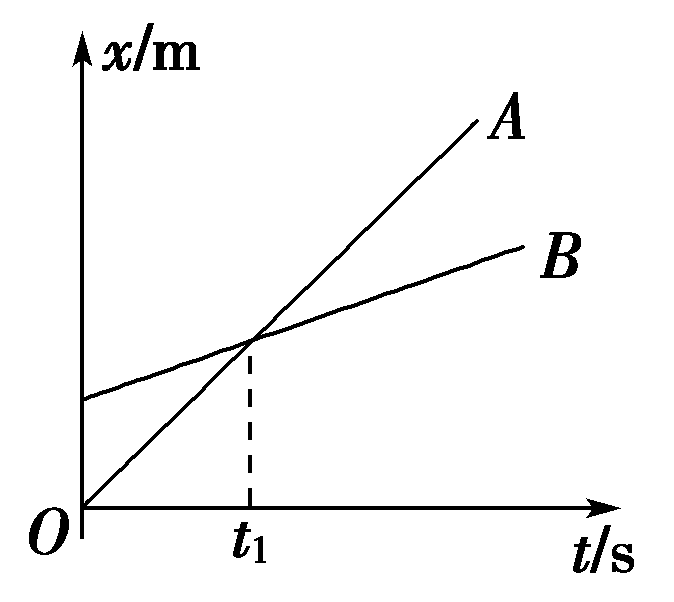．如图是A、B两个质点做直线运动的位移-时间图象。则（    ）

（A）在运动过程中，A质点总比B质点运动得快

（B）在0～t₁这段时间内，两质点的位移相同

（C）当t＝t₁时，两质点的速度相等

（D）当t＝t₁时，A、B两质点的加速度不相等

【答案】

A

【解析】

位移-时间图象中，图线的斜率对应物体的速度，所以A质点的速度比B质点的速度快，A正确。位移-时间图象中，位移等于初、末时刻对应的纵坐标的坐标差，所以在0～t₁这段时间内，A质点的位移大于B质点的位移，B错误。t₁时刻时，两图象的斜率不同，两质点的速度不同，C错误。两物体都做匀速直线运动，加速度都等于零，D错误。

 

32．下列图中表示物体做匀变速直线运动的图象是（    ）

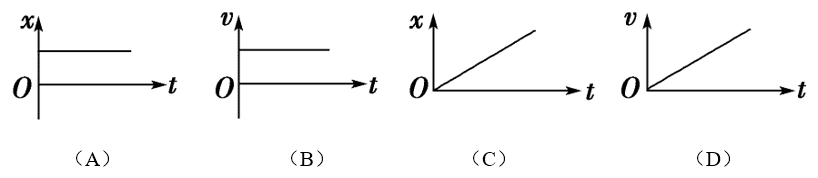
【答案】

D

【解析】

匀变速直线运动的v-t图象是一条倾斜直线，x-t图象是一条曲线．A中图象表示物体静止，B、C中图象表示物体做匀速直线运动，D中图象表示物体做匀加速直线运动，D正确。

 

33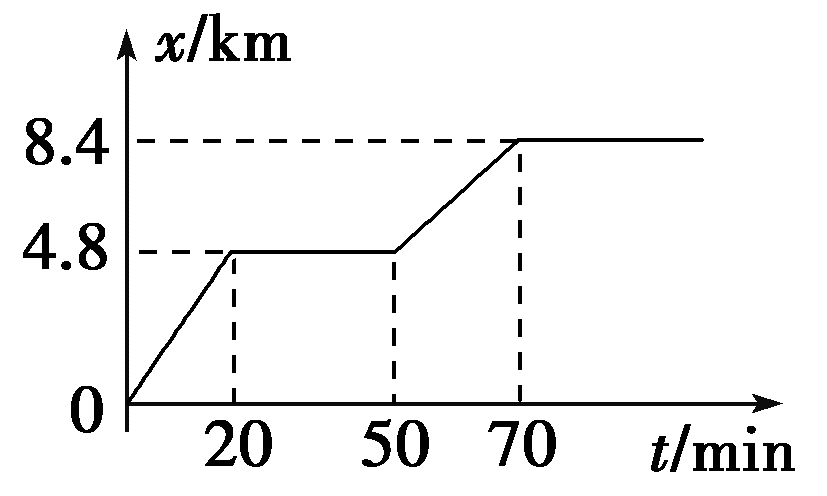．甲、乙两位同学在放学时，从学校所在地骑自行车沿平直的公路回家，先到乙同学家，休息一会，甲同学继续骑车前行，在70 min时到家，甲同学的x-t图象如图所示，下列说法正确的是（    ）

（A）在前20 min内甲同学做匀加速运动

（B）甲同学在乙同学家停留了50 min

（C）甲、乙两同学家相距3.6 km

（D）甲从离开学校至到家的这段时间内，平均速度为2 m/s

【答案】

CD

【解析】

前20 min，甲同学做匀速直线运动，A错。20～50 min甲同学一直在乙同学家，共停留30 min，B错。甲、乙两同学家的距离为8.4 km－4.8 km＝3.6 km，C对。甲同学从学校到家的位移x＝8.4 km，所用时间t＝70 min＝4 200 s，平均速度v＝\(\frac{x}{t}\)＝\(\frac{{8.4 \times {{10}^3}}}{{4200}}\) m/s＝2 m/s，D对。

 

34．汽车从A点由静止开始沿直线ACB做匀变速直线运动，第4 s末通过C点时关闭发动机做匀减速运动，再经6 s到达B点停止，总共通过的位移是30 m，则下列说法正确的是（    ）

（A）汽车在AC段与BC段的平均速度相同

（B）汽车通过C点时的速度为3 m/s

（C）汽车通过C点时的速度为6 m/s

（D）AC段的长度为12 m

【答案】

ACD

【解析】

设汽车通过C点时的速度为v_C，由\(\bar v\)＝\(\frac{{{v_1} + {v_2}}}{2}\)可知，汽车在AC段与BC段的平均速度均为\(\bar v\)＝\(\frac{{{v_C}}}{2}\)，A正确；由\(\frac{{{v_C}}}{2}\)t₁＋\(\frac{{{v_C}}}{2}\)t₂＝x_AB，t₁＋t₂＝10 s可得v_C＝6 m/s，C正确，B错误；由x_AC＝t₁可得：x_AC＝12 m，D正确。

 

35．做匀减速直线运动的物体经4 s停止，若在4 s内的位移是32 m，则最后1 s内的位移是（     ）

（A）3.5 m           （B）2 m             （C）1 m      （D）0

【答案】

B

【解析】

利用“逆向思维法”，把物体的运动看成逆向的初速度为零的匀加速直线运动，4 s内的位移x＝\(\frac{1}{2}\)at²，最后1 s内的位移xʹ=\(\frac{1}{2}\)atʹ²，所以\(\frac{x}{{x'}}\)＝\(\frac{{{t^2}}}{{{{t'}^2}}}\)，xʹ＝2 m，故选项B正确。

 

36．做匀变速直线运动的物体，加速度大小为a，在时间t内位移为s，末速度为v，则（      ）

（A）s＝vt＋\(\frac{1}{2}\)at²        （B）s＝－vt＋\(\frac{1}{2}\)at²

（C）s＝－vt－\(\frac{1}{2}\)at²        （D）s＝vt－\(\frac{1}{2}\)at²

【答案】

D

【解析】

利用逆向思维法，将匀加速直线运动的物体看做是初速度为v，加速度大小为a的匀减速直线运动，则x＝vt－\(\frac{1}{2}\)at²，D正确。

 

37．关于匀变速直线运动，下列说法正确的是（    ）

（A）位移与时间的平方成正比

（B）位移总是随着时间的增加而增加

（C）加速度、速度、位移三者方向一致

（D）加速度、速度、位移的方向并不一定都相同

【答案】

D

【解析】

根据x＝v₀t＋\(\frac{1}{2}\)at²，位移与时间的平方不是正比关系，A错误。位移可能随时间的增加而增加，也可能随时间的增加而减小，如先减速后反向加速的匀变速直线运动，位移先增加后减小，B错误。加速度、速度、位移的方向可能相同，也可能不同，C错误，D正确。

 

38．对于一做单向匀减速运动的物体，在静止前下列说法中正确的是（     ）

（A）速度越来越小，位移也越来越小

（B）速度越来越小，位移越来越大

（C）加速度越来越小，位移越来越大

（D）加速度越来越小，位移越来越小

【答案】

B

【解析】

物体朝一个方向运动，故位移不断增大，只有B对。

 

39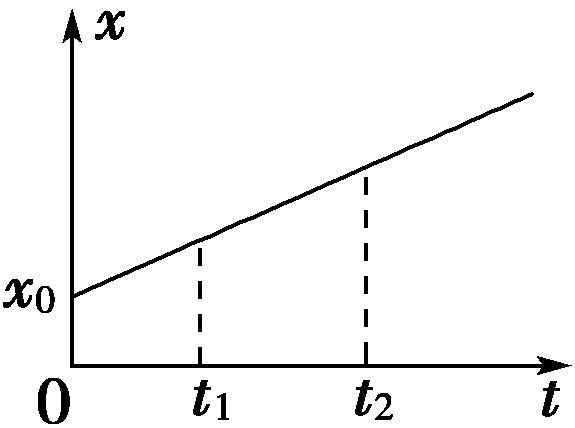．一质点沿一条直线运动的位移-时间图象如图所示，则（    ）

（A）t＝0时刻，质点在坐标原点

（B）从t＝0时刻到t₁时刻，质点位移是x₀

（C）从t₁时刻到t₂时刻，质点位移大小等于路程

（D）质点在t₁时刻的速度比t₂时刻的速度大

【答案】

C

【解析】

t＝0时刻，质点在x₀处，选项A错误；从t＝0时刻到t₁时刻，质点位移大于x₀，选项B错误；从t₁时刻到t₂时刻，质点做单方向匀速直线运动，位移大小等于路程，选项C正确，选项D错误。

 

40．飞机的起飞过程是从静止出发，在直跑道上加速前进，等达到一定速度时离地。已知飞机加速前进的路程为1 600 m，所用的时间为40 s。假设这段时间内的运动为匀加速运动，用a表示加速度，v表示离地时的速度，则（    ）

（A）a＝2 m/s²，v＝80 m/s              （B）a＝2 m/s²，v＝40 m/s

（C）a＝80 m/s²，v＝40 m/s             （D）a＝40 m/s²，v＝80 m/s

【答案】

A

【解析】

由x＝\(\frac{1}{2}\)at²，

得a＝\(\frac{{2x}}{{{t^2}}}\)＝\(\frac{{2 \times 1600}}{{{{40}^2}}}\) m/s²＝2 m/s²

由x＝\(\frac{v}{2}\)t，

得v＝\(\frac{{2x}}{t}\)＝\(\frac{{2 \times 1600}}{{40}}\) m/s＝80 m/s

 

41．在交警处理某次交通事故时，通过监控仪器扫描，输入计算机后得到汽车在水平路面上刹车过程中的位移随时间变化的规律为：x＝30t－3t²（x的单位是m，t的单位是s）。则该汽车在路面上留下的刹车痕迹长度为（     ）

（A）25 m           （B）50 m            （C）75 m            （D）150 m

【答案】

C

【解析】

由x＝v₀t＋\(\frac{1}{2}\)at²得v₀＝30 m/s，\(\frac{1}{2}\)a＝－3 m/s²，即a＝－6 m/s2。汽车由v₀刹车到静止，由v＝v₀＋at得t＝\(\frac{{v - {v_0}}}{a}\)＝5 s，汽车在路面上留下的刹车痕迹长度，由x＝v₀t＋\(\frac{1}{2}\)at²得x＝30 m/s×5 s＋\(\frac{1}{2}\)×（－6 m/s²）×（5 s）²＝75 m，故选项C正确。

 

42．由静止开始做匀加速直线运动的火车，在第10 s末的速度为2 m/s，下列叙述中正确的是（     ）

（A）前10 s内通过的位移为10 m

（B）每秒速度变化0.2 m/s

（C）10 s内平均速度为1 m/s

（D）第10 s内通过2 m

【答案】

ABC

 

43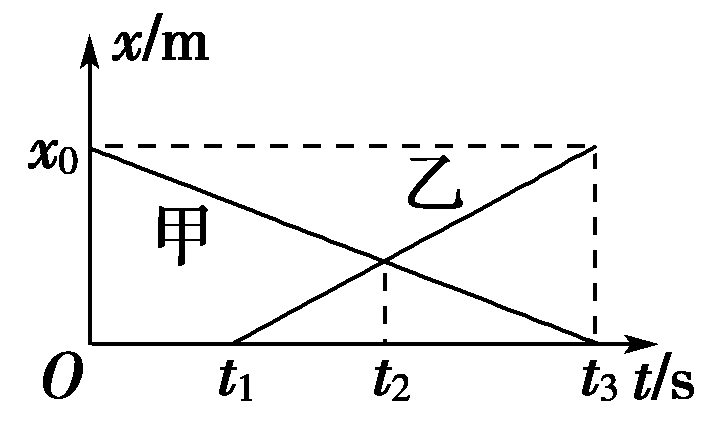．如图是做直线运动的甲、乙两物体的位移-时间图象，由图象可知（    ）

（A）甲启动的时间比乙早t₁秒

（B）当t＝t₂时，两物体相遇

（C）当t＝t₂时，两物体相距最远

（D）当t＝t₃时，两物体相距x₀米

【答案】

ABD

【解析】

由位移-时间图象知甲启动的时间比乙早t₁秒，A正确；当t＝t₂时，两物体在同一位置，即相遇，B正确，C错误；当t＝t₃时，甲位于原点，乙位于离原点x₀米处，两物体相距x₀米，D正确。

 

44．一物体从斜面顶端由静止开始匀加速下滑，设斜面足够长，最初3秒的位移为x₁，第2个3秒内的位移为x₂，且x₂－x₁＝1.8 m。试求：

（1）x₁、x₂分别为多大；

（2）物体下滑的加速度；

（3）6 s末的速度。

【答案】

（1）0.9 m，2.7 m

（2）0.2 m/s²

（3）1.2 m/s

 

45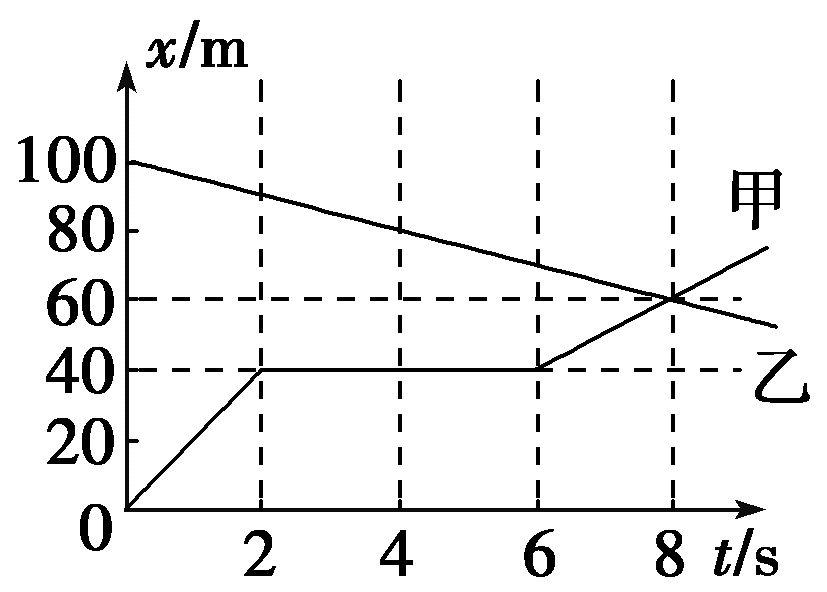．如图所示，折线表示物体甲从A地向B地运动的x－t图象，直线表示物体乙从B地向A地运动的x－t图象，则下列说法正确的是（    ）

（A）在2～6 s内，甲做匀速直线运动

（B）乙做匀速直线运动，其速度大小为5 m/s

（C）从计时开始至甲、乙相遇的过程中，乙的位移大小为60 m

（D）在t＝8 s时，甲、乙两物体的速度大小相等

【答案】

B

 

46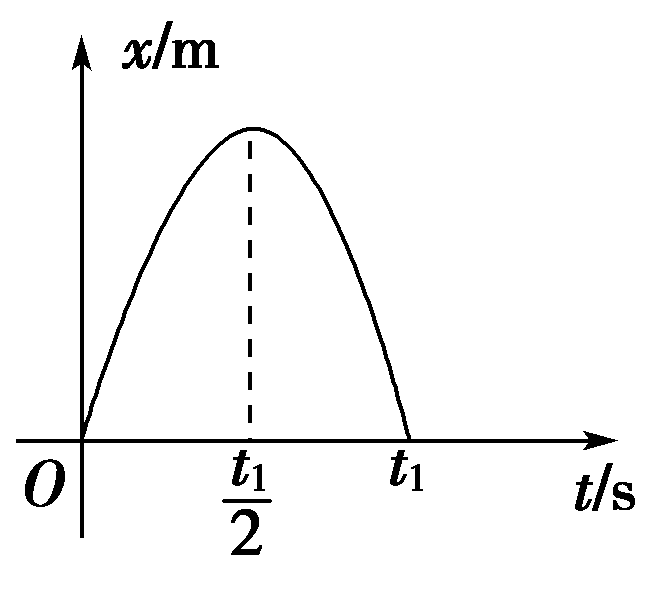．一质点的x-t图象如图所示，那么此质点的v-t图象可能是下图中的（    ）

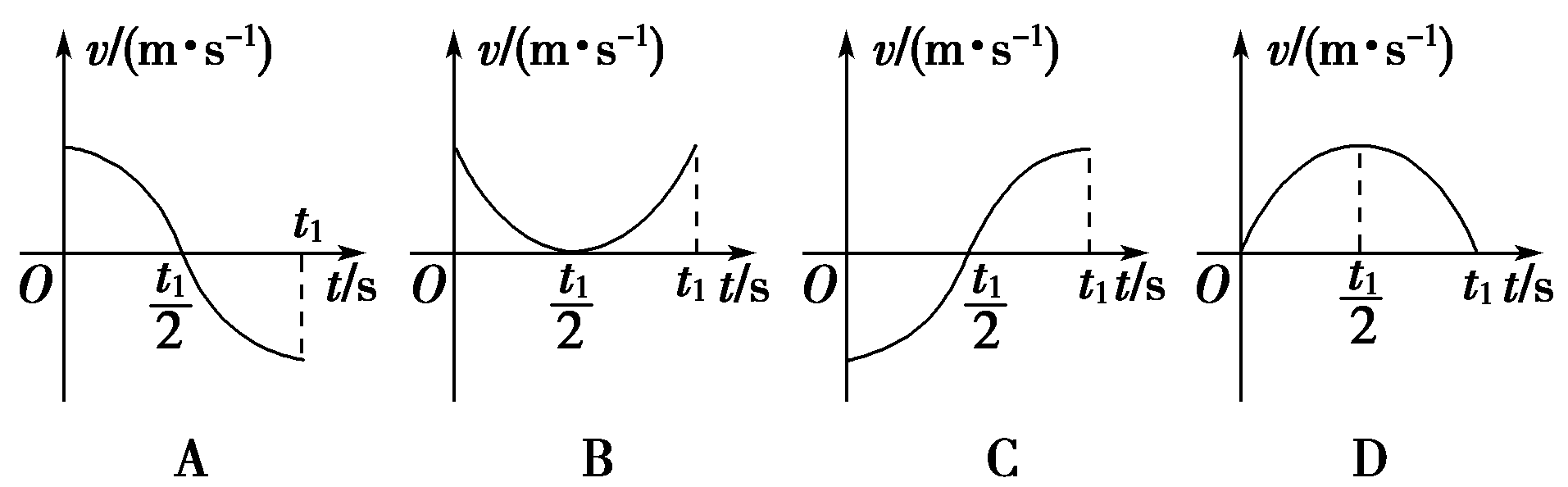
【答案】

A

【解析】

x-t图象的切线斜率表示速度，由图象可知：0～\(\frac{{{t_1}}}{2}\)时间内图象的斜率为正且越来越小，在\(\frac{{{t_1}}}{2}\)时刻图象斜率为0，即物体正向速度越来越小，\(\frac{{{t_1}}}{2}\)时刻减为零；从\(\frac{{{t_1}}}{2}\)～t₁时间内，斜率为负值，数值越来越大，即速度反向增大，故选项A正确。

 

47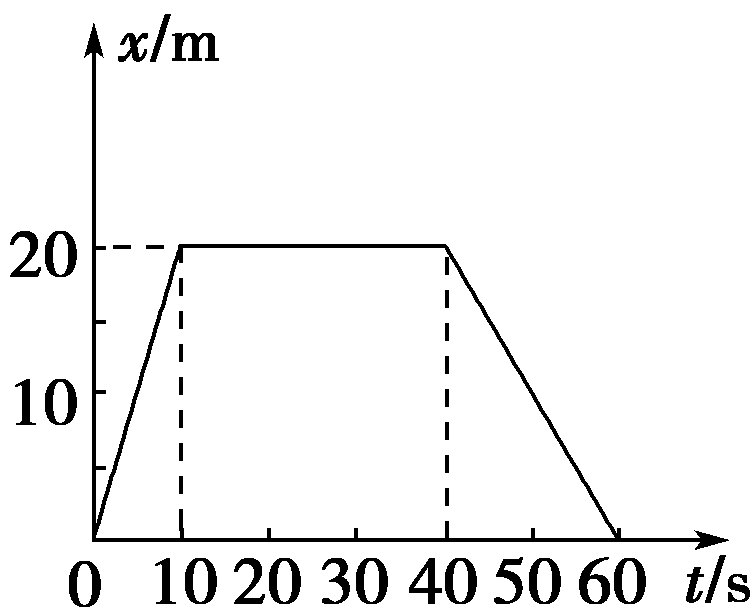．如图所示是一个物体沿直线运动的x-t图象。求：

（1）第5秒末的速度大小；

（2）0～60秒内的总路程；

（3）在v－t坐标中作出0～60 s内物体的速度-时间图象。

【答案】

如图所示是一个物体沿直线运动的x-t图象。求：

（1）第5秒末的速度大小；

（2）0～60秒内的总路程；

（3）在v－t坐标中作出0～60 s内物体的速度-时间图象。

【解析】

（1）0～10 s内匀速运动的速度v₁＝\(\frac{{{x_1}}}{{{t_1}}}\)＝\(\frac{20}{10}\) m/s=2 m/s，即第5秒末的速度大小为2 m/s

（2）0～10 s内的路程d₁＝20 m，

10～40 s内的路程d₂＝0，

40～60 s内的路程d₃＝20 m，

所以0～60 s内的总路程d＝40 m

（3）0～10 s内速度为2 m/s，

10～40 s内速度为0，

40～60 s内速度v₂＝\(\frac{{{x_2}}}{{{t_2}}}\)＝\(\frac{20}{20}\) m/s＝1 m/s，

方向与原速度方向相反，速度-时间图象如图所示。

 

48．一辆巡逻车最快能在10 s内由静止加速到最高速度50 m/s，并能保持这个速度匀速行驶，问该巡逻车在平直的高速公路上由静止开始追上前方2 000 m处正以35 m/s的速度匀速行驶的汽车，至少需要多长时间？（巡逻车加速过程的加速度恒定）

【答案】

150 s

【解析】

巡逻车加速过程位移

x＝\(\frac{{{v_m}}}{2}\)t₀＝250 m<2 000 m＋x_汽车，

所以巡逻车先加速再匀速才能追上汽车．

设巡逻车至少需要时间t才能追上汽车，则有：

x_巡逻＝250＋v_m（t－10），

x_汽车＝vt，

x_巡逻＝2 000＋x_汽车，

解得t＝150 s

 

49．某种类型的飞机起飞滑行时，从静止开始做匀加速运动，加速度大小为4 m/s²，飞机速度达到80 m/s时离开地面升空。如果在飞机达到起飞速度时，突然接到命令停止起飞，飞行员立即使飞机制动，飞机做匀减速运动，加速度大小为5 m/s²。如果要求你为该类型的飞机设计一条跑道，使在这种特殊情况下，飞机不滑出跑道，你设计的跑道长度至少要多长？

【答案】

1 440 m

 

50．物体先做初速度为零的匀加速运动，加速度大小为a₁，当速度达到v时，改为以大小为a₂的加速度做匀减速运动，直至速度为零。在加速和减速过程中物体的位移和所用时间分别为x₁、t₁和x₂、t₂，下列各式成立的是（     ）

（A）\(\frac{{{x_1}}}{{{x_2}}}\)＝\(\frac{{{t_1}}}{{{t_2}}}\)          （B）\(\frac{{{a_1}}}{{{a_2}}}\)＝\(\frac{{{t_1}}}{{{t_2}}}\)          （C）\(\frac{{{x_1}}}{{{x_2}}}\)＝\(\frac{{{a_2}}}{{{a_1}}}\)          （D）\(\frac{{{x_1}}}{{{x_2}}}\)＝\(\frac{{{a_1}}}{{{a_2}}}\)

 

【答案】

AC

【解析】

在加速运动阶段v²＝2a₁x₁，v＝a₁t₁；在减速运动阶段0－v²＝2（－a₂）x_2，0－v＝－a₂t₂.由以上几式可得\(\frac{{{x_1}}}{{{x_2}}}\)＝\(\frac{{{a_2}}}{{{a_1}}}\)，\(\frac{{{a_1}}}{{{a_2}}}\)＝\(\frac{{{t_2}}}{{{t_1}}}\)  ，进一步可得\(\frac{{{x_1}}}{{{x_2}}}\)＝\(\frac{{{t_1}}}{{{t_2}}}\)，选项A、C正确。

 

51．已知长为L的光滑斜面，物体从斜面顶端由静止开始以恒定的加速度下滑，当物体的速度是到达斜面底端速度的\(\frac{1}{3}\)时，它沿斜面已下滑的距离是（    ）

（A）\(\frac{L}{3}\)        （B）\(\frac{L}{9}\)          （C）\(\frac{{\sqrt 3 L}}{3}\)            （D）\(\frac{L}{6}\)

【答案】

B

 

52．光滑斜面的长度为L，一物体自斜面顶端由静止开始匀加速滑至底端，经历的时间为t，则下列说法正确的是（    ）

（A）物体运动全过程中的平均速度是\(\frac{L}{t}\)

（B）物体在\(\frac{t}{2}\)时的瞬时速度是\(\frac{{2L}}{t}\)

（C）物体运动到斜面中点时瞬时速度是\(\frac{{\sqrt 2 L}}{t}\)

（D）物体从顶点运动到斜面中点所需的时间是\(\frac{{\sqrt 2 t}}{2}\)

【答案】

ACD

 

53．一列火车由静止以恒定的加速度启动出站，设每节车厢的长度相同，不计车厢间间隙距离，一观察者站在第一节车厢最前面，他通过测时间估算出第一节车厢尾驶过他时的速度为v₀，则第n节车厢尾驶过他时的速度为（     ）

（A）nv₀              （B）n²v₀             （C）\(\sqrt n \)v₀            （D）2nv₀

【答案】

C

 

54．一滑雪运动员从85 m长的山坡上匀加速滑下，初速度是1.8 m/s，末速度是5.0 m/s，滑雪运动员通过这段斜坡需要多长时间？

【答案】

25 s

 

55．关于公式x＝\(\frac{{{v^2} - v_0^2}}{{2a}}\)，下列说法正确的是（     ）

（A）此公式只适用于匀加速直线运动

（B）此公式适用于匀变速直线运动

（C）此公式只适用于位移为正的情况

（D）此公式不可能出现a、x同时为负值的情况

【答案】

B

【解析】

公式x＝\(\frac{{{v^2} - v_0^2}}{{2a}}\)既适用于匀加速直线运动，也适用于匀减速直线运动，既适用于位移为正的情况，也适用于位移为负的情况，选项B正确，选项A、C错误．当物体做匀加速直线运动，且规定初速度的反方向为正方向时，a、x就会同时为负值，选项D错误。

 

56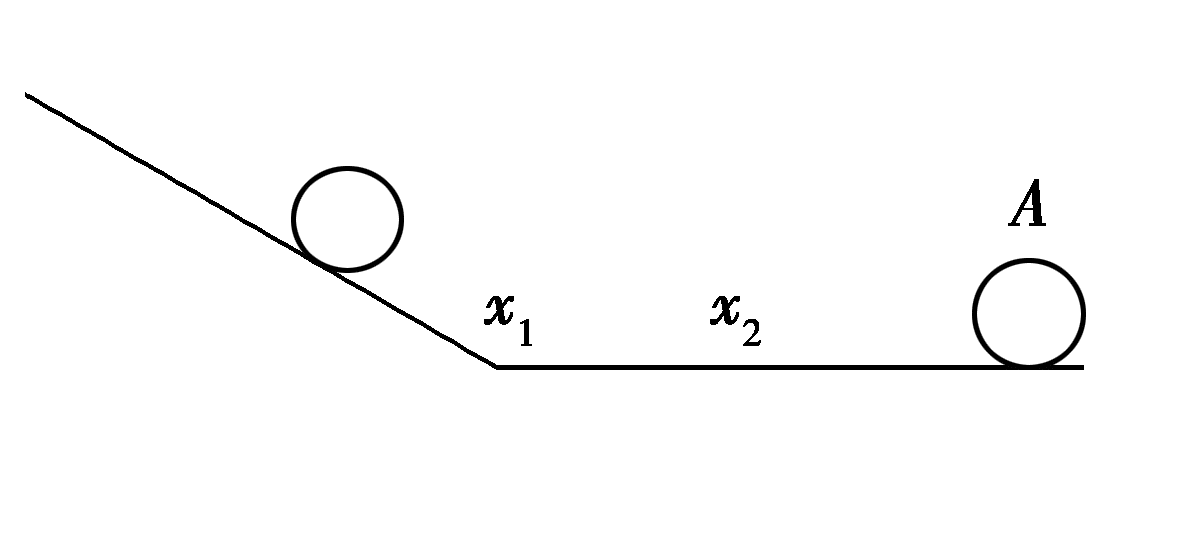．如图所示，物体A在斜面上由静止匀加速滑下x₁后，又匀减速地在平面上滑过x₂后停下，测得x₂＝2x₁，则物体在斜面上的加速度a₁与在平面上的加速度a₂的大小关系为（    ）

（A）a₁＝a₂                （B）a₁＝2a₂

（C）a₁＝\(\frac{1}{2}\)a₂              （D）a₁＝4a₂

【答案】

B

【解析】

物体在斜面上初速度为零，设末速度为v，则有v²－0＝2a₁x₁。同理，在水平面上有v²－0＝2a₂x₂，所以a₁x₁＝a₂x₂，故a₁＝2a₂。

 

57．一辆汽车做匀加速直线运动，初速度为4 m/s，经过4 s速度达到12 m/s，下列说法中不正确的是（     ）

（A）汽车的加速度为2 m/s²

（B）汽车每秒速度的变化量为2 m/s

（C）汽车的平均速度为6 m/s

（D）汽车的位移为32 m

【答案】

C

 

58．汽车刹车后做匀减速直线运动，经3 s后停止运动，那么，在这连续的三个1 s内汽车通过的位移之比为（    ）

（A）1∶3∶5      （B）5∶3∶1

（C）1∶2∶3      （D）3∶2∶1

【答案】

B

【解析】

用逆向思维可以把汽车刹车的运动认为是初速度为零的匀加速直线运动的逆过程，所以这连续的三个1 s内汽车通过的位移之比为5∶3∶1，B项对。

 

59．汽车给人们生活带来极大便利，但随着车辆的增多，交通事故也相应增加。为了安全，在行驶途中，车与车之间必须保持一定的距离，因为从驾驶员看见某一情况到采取制动动作的时间里，汽车仍然要通过一段距离（称为思考距离），而从采取制动动作到车完全静止的时间里，汽车又要通过一段距离（称为制动距离）。下表给出了驾驶员驾驶的汽车在不同速度下的思考距离和制动距离等部分数据。某同学分析这些数据，算出了表格中未给出的数据X、Y，该同学计算正确的是（    ）

速度（m/s）	思考距离（m）	制动距离（m）
10	12	20
15	18	X
20	Y	80
25	30	125

（A）X＝40，Y＝24          （B）X＝45，Y＝24

（C）X＝60，Y＝22          （D）X＝40，Y＝21

【答案】

B

【解析】

汽车做匀速运动，由x＝vt知

t＝\(\frac{x}{v}\)＝1.2 s，

所以Y＝v₁t＝20×1.2 m＝24 m.

制动距离是汽车做匀减速运动的位移，由v²＝2ax知

a＝\(\frac{{{v^2}}}{{2x}}\)＝\(\frac{{100}}{{40}}\) m/s²＝2.5 m/s²，

由v₂²＝2aX，

得X＝\(\frac{{v_2^2}}{{2a}}\)＝\(\frac{{{{15}^2}}}{{2 \times 2.5}}\) m＝45 m

 

60．我国的高速铁路技术不断创出新的纪录，同时旅客的安全工作更引起了人们的广泛关注。假设某次列车在离车站9.5 km处开始制动刹车，此时列车的速度为342 km/h，列车匀减速到站并刚好停住。求：

（1）该列车进站时的加速度多大？

（2）列车减速运动的时间为多少？

【答案】

（1）0.475 m/s²

（2）200 s

 

61．如图所示，木块A、B并排且固定在水平桌面上，A的长度是L，B的长度是2L。一颗子弹沿水平方向以速度v₁射入A，以速度v₂穿出B。子弹可视为质点，其运动视为匀变速直线运动，则子弹穿出A时的速度为（    ）

（A）\(\frac{{2{v_1} + {v_2}}}{3}\)              （B）\(\sqrt {\frac{{2v_1^2 + 2v_2^2}}{3}} \)               （C）\(\sqrt {\frac{{2v_1^2 + v_2^2}}{3}} \)               （D）\(\frac{2}{3}\)v₁

【答案】

C

【解析】

设子弹在木块中的加速度为a，则

v₂²－v₁²＝2a·3L，①

v_A²－v₁²＝2a·L，②

由①②两式得子弹穿出A时的速度

v_A＝\(\sqrt {\frac{{2v_1^2 + v_2^2}}{3}} \) ，选项C正确。

 

62．如图所示，光滑斜面被分成四个长度相等的部分，一个物体由A点静止释放，下面结论中正确的是（    ）

（A）物体到达各点的速度v_B∶v_C∶v_D∶v_E＝1∶\(\sqrt 2 \)∶\(\sqrt 3 \)∶2

（B）物体到达各点所经历的时间t_B∶t_C∶t_D∶t_E＝1∶\(\sqrt 2 \)∶\(\sqrt 3 \)∶2

（C）物体从A到E的平均速度\(\bar v\)＝v_B

（D）通过每一部分时，其速度增量均相等

【答案】

ABC

【解析】

设每一部分的长度为x，根据v²－v₀²＝2ax得v_B²＝2ax，v_C²＝2a·2x，v_D²＝2a·3x，v_E²＝2a·4x，所以v_B∶v_C∶v_D∶v_E＝1∶\(\sqrt 2 \)∶\(\sqrt 3 \)∶2，A正确；根据x＝\(\frac{1}{2}\)at²得t_B＝\(\sqrt {\frac{{2 \cdot x}}{a}} \)，t_C＝\(\sqrt {\frac{{2 \cdot 2x}}{a}} \)，t_D＝\(\sqrt {\frac{{2 \cdot 3x}}{a}} \)，t_E＝\(\sqrt {\frac{{2 \cdot 4x}}{a}} \)，所以t_B∶t_C∶t_D∶t_E＝1∶\(\sqrt 2 \)∶\(\sqrt 3 \)∶2，B正确；从A到E的平均速度等于中间时刻的速度，从A到E的时间为t_E＝\(\sqrt {\frac{{2 \cdot 4x}}{a}} \)，中间时刻为\(\frac{1}{2}\)t_E＝\(\sqrt {\frac{{2 \cdot 4x}}{4a}} \)＝\(\sqrt {\frac{{2 \cdot x}}{a}} \)＝t_B，所以\(\bar v\)＝v_B，C正确；由v_B、v_C、v_D、v_E的大小知每一部分的速度增量不相等，D错误。

 

63．我国的第一艘航空母舰“辽宁号”经过多次海试，正式入役了，各类武器装备已经上舰。固定翼飞行器从航空母舰起飞的方式可以分两种，第一种是飞机弹射器起飞，第二种是斜板滑跳起飞，有专家指出，中国目前也在试验蒸汽弹射技术。某型号航空母舰上装有帮助飞机起飞的弹射系统，已知某型号的飞机在跑道上加速时可能产生的最大加速度为5.0 m/s²，当飞机的速度达到50 m/s时才能离开航空母舰起飞．设航空母舰处于静止状态。问：

（1）若要求该飞机滑行160 m后起飞，弹射系统必须使飞机具有多大的初速度？

（2）若某舰上不装弹射系统，要求该型号飞机仍能在此舰上正常起飞，问该舰身长至少应为多长？

【答案】

（1）30 m/s

（2）250 m

【解析】

（1）设弹射系统帮助该飞机起飞时初速度为v₀，

由运动学公式v²－v₀²＝2ax，

可知v₀＝\(\sqrt {{v^2} - 2ax} \)＝30 m/s

（2）不装弹射系统时，飞机从静止开始做匀加速直线运动．

由公式v²＝2ax，可知该舰身长至少应为x＝\(\frac{{{v^2}}}{{2a}}\)＝250 m

 

64．如图所示，隧道是高速公路上的特殊路段也是事故多发路段之一。某日，一轿车A因故恰停在隧道内离隧道入口d＝50 m的位置。此时另一辆轿车B正以v₀＝90 km/h的速度匀速向隧道口驶来，轿车B的驾驶员在进入隧道口时，才发现停在前方的轿车A并立即采取制动措施．假设该驾驶员反应时间t₁＝0.57 s，轿车制动系统响应时间（开始踏下制动踏板到实际制动）t₂＝0.03 s，轿车制动时产生的加速度为7.5 m/s²。

（1）试通过计算说明该轿车B会不会与停在前面的轿车A相撞？

（2）若会相撞，那么撞前瞬间轿车B速度大小为多少？若不会相撞，那么停止时与轿车A的距离为多少？

【答案】

（1）会相撞

（2）10 m/s

【解析】

（1）轿车实际制动前0.6 s内做匀速直线运动，匀速运动的位移为x₁＝\(\frac{{90}}{{3.6}}\)×0.6 m＝15 m，实际制动中的加速度大小a＝7.5 m/s²，实际制动中当速度减为零时的位移x₂＝\(\frac{{v_0^2}}{{2a}}\)＝\(\frac{{{{(\frac{{90}}{{3.6}})}^2}}}{{2 \times 7.5}}\) m＝\(\frac{{125}}{3}\) m，由于x₁＋x₂＝\(\frac{{170}}{3}\) m＝56.7 m>50 m，故B会与停在前面的轿车A相撞。

（2）设与A相碰时的速度为v，根据运动学公式得：－2×7.5×（50－15） m＝v²－(\(\frac{{90}}{{3.6}}\))²，解得v＝10 m/s。

 

65．一个铁钉和一团棉花同时从同一高处下落，总是铁钉先落地，这是因为（    ）

（A）铁钉比棉花团重

（B）棉花团受到的空气阻力不能忽略

（C）棉花团的加速度比重力加速度小

（D）铁钉的重力加速度比棉花团的重力加速度大

【答案】

BC

【解析】

铁钉受到的空气阻力与其重力相比较小，可以忽略，而棉花受到的空气阻力与其重力相比较大，不能忽略，所以铁钉的下落加速度较大，而它们的重力加速度是相同的，故只有B、C正确。

 

66．关于自由落体运动，下列说法正确的是（     ）

（A）自由落体运动是一种匀变速直线运动

（B）物体刚下落时，速度和加速度都为零

（C）物体的质量越大，下落时加速度就越大

（D）当地重力加速度为9.8 m/s²，则物体在该处自由下落的过程中，每秒速度都增加9.8 m/s

【答案】

AD

【解析】

自由落体运动是初速度为零的匀加速直线运动，A对，B错。所有物体做自由落体运动时，下落的加速度都是重力加速度，C错。由v＝gt知，物体做自由落体运动时每秒速度的增加量都等于重力加速度的大小，D对。

 

67．如图所示，悬挂的直杆AB长为a，在B端以下h处有一长为b的无底圆柱筒CD，若将悬线剪断，问：

（1）直杆下端B穿过圆柱筒的时间是多少？

（2）整个直杆AB穿过圆柱筒的时间是多少？

【答案】

（1）\(\sqrt {\frac{{2(h + b)}}{g}} \)－\(\sqrt {\frac{{2h}}{g}} \)

（2）\(\sqrt {\frac{{2(h + a + b)}}{g}} \)－\(\sqrt {\frac{{2h}}{g}} \)

【解析】

（1）直杆下端B下落到C（下落h）开始进入圆柱筒，当直杆下端B下落到D（下落h＋b）时穿出圆柱筒。

由x＝\(\frac{1}{2}\)gt²得t＝\(\sqrt {\frac{{2x}}{g}} \)

则B下落到C点所需时间为t₁＝\(\sqrt {\frac{{2h}}{g}} \)，

B下落到D点所需时间t₂＝\(\sqrt {\frac{{2(h + b)}}{g}} \)

则直杆下端B穿过圆柱筒的时间是

Δt₁＝t₂－t₁＝\(\sqrt {\frac{{2(h + b)}}{g}} \)－\(\sqrt {\frac{{2h}}{g}} \)

（2）整个直杆AB穿过圆柱筒，从B下落到C点（自由下落h）起到A下落到D点（自由下落h＋a＋b）止。

同理可得整个直杆AB穿过圆柱筒的时间是

Δt₂＝ \(\sqrt {\frac{{2(h + a + b)}}{g}} \)－\(\sqrt {\frac{{2h}}{g}} \)

 

68．关于自由落体运动，下列说法正确的是（     ）

（A）速度变化得越来越快

（B）在开始连续的三个1 s内通过的位移之比是1∶4∶9

（C）第1 s末、第2 s末、第3 s末的速度大小之比是1∶2∶3

（D）物体的质量越大，加速度越大

【答案】

C

【解析】

物体自由落体的加速度为g，大小不变，A、D均错误；由v＝gt可得，v₁∶v₂∶v₃＝1∶2∶3，C正确；从开始运动三个连续1 s内通过的位移之比为1∶3∶5，B错误。

 

69．为了测出楼房的高度，让一石块从楼顶自由落下（不计空气阻力），测出下列哪个 物理量不能算出楼房的高度（    ）

（A）石块下落到地面的总时间

（B）石块经过楼上一个1.8 m高的窗户所用的时间

（C）石块落地前最后一秒的位移

（D）石块通过最后一米位移的时间

【答案】

B

【解析】

由石块的落地时间可以求出楼的高度；由石块通过最后一米位移的时间也可以求出楼的高度；由最后1 s位移，可求得最后1 s的平均速度，此平均速度就是落地前0.5 s的瞬时速度，再求落地速度即可求出楼房高度；所以A、C、D项可以求出楼的高度；知道经过楼上1.8 m高的窗户所用的时间，由v₀t＋\(\frac{1}{2}\)gt²＝h可以求出楼顶到窗户的高度但无法求楼的高度，所以B项不能求楼的高度。

 

70．某物理兴趣小组为获得当地重力加速度值，设计了如下实验，并进行了一系列探究 过程。假设你也是其中一员，请补充完整横线部分内容。

（1）操作过程：

①将打点计时器固定在铁架台上，如图所示；

②将接有重物的纸带沿竖直方向穿过打点计时器的限位孔；

③先____________，再释放纸带；

④获得点迹清晰的几条纸带。

（2）探究过程：其中一条纸带的点迹及数据如图所示。（图中直尺的单位为cm，点O为纸带上记录到的第一点，点A、B、C、D…依次表示点O以后连续的各点，已知打点计时器每隔T＝0.02 s打一个点。

①小组成员量出DF间的距离为3.60 cm，计算出打点计时器打下点E时的速度v_E＝____________m/s；

②小组成员量出FH间的距离为5.20 cm，计算出打点计时器打下点G时的速度v_G＝____________m/s；

③利用a＝得出g＝____________m/s²；

④利用a＝得出g＝____________m/s²。

【答案】

（1）③接通电源

（2）①0.90，②1.30，③10.00，④10.00

 

71．如图所示是用照相机对一小球做自由落体运动频闪拍摄的照片，符合实际的是（     ）

（A）    （B）    （C）    （D）

【答案】

D

【解析】

因频闪拍摄的频率是固定的，因此，小球做自由落体运动，越向下运动，相邻小球之间的距离越大，故D正确。

 

72．在一次利用滴水法测重力加速度的实验中：让水龙头的水一滴一滴地滴在其正下方的盘子里，调整水龙头，让前一滴水滴到盘子而听到声音时，后一滴恰好离开水龙头．从第1次听到水击盘声时开始数“1”并开始计时，数到“n”时听到水击盘声的总时间为T，用刻度尺量出水龙头到盘子的高度差为h，即可算出重力加速度。则  （     ）

（A）每一滴水从水龙头落到盘子的时间为\(\frac{T}{n}\)

（B）每一滴水从水龙头落到盘子的时间为\(\frac{T}{{n - 1}}\)

（C）重力加速度的计算式为\(\frac{{2{n^2}h}}{{{T^2}}}\)

（D）重力加速度的计算式为\(\frac{{2{{(n - 1)}^2}h}}{{{T^2}}}\)

【答案】

BD

【解析】

从第1次听到水击盘声开始计数为“1”，当数到“n”时，共经历了n－1个水滴下落的时间，故每一滴水从水龙头落到盘子的时间为t＝\(\frac{T}{{n - 1}}\)，A错误，B正确；由h＝\(\frac{1}{2}\)gt²，可得：g＝\(\frac{{2{{(n - 1)}^2}h}}{{{T^2}}}\)，C错误，D正确。

 

73．在塔顶上将一物体竖直向上抛出，抛出点为A，物体上升的最大高度为20 m，不计空气阻力，g取10 m/s²，设塔足够高，则物体位移大小为10 m时，物体通过的路程不可能为（    ）

（A）10 m           （B）20 m            （C）30 m            （D）50 m

【答案】

B

【解析】

取竖直向上为正方向，当物体位于抛出点上方时，即x₁＝10 m，其路程可能为：s₁＝x₁＝10 m，故A可能；s₂＝H＋（H－x₁）＝30 m，故C可能；当物体位于抛出点下方时，即x₂＝－10 m，其路程为：

s₂＝2H＋|x₂|＝50 m，

故D可能、B不可能。

 

74．意大利科学家伽利略在研究落体运动的规律时，做了著名的斜面实验，其中应用到的物理思想方法属于（    ）

（A）等效替代                          （B）实验归纳

（C）理想实验                         （D）控制变量

【答案】

C

【解析】

伽利略在研究落体运动的规律时，做了著名的斜面实验，斜面的摩擦力忽略不计，而逐渐增大斜面的倾斜角，当倾角等于90°时物体竖直下落，这种物理思想方法属于理想实验，故选项C正确。

 

75．下列说法正确的是（    ）

（A）亚里士多德认为物体下落的快慢与物体的轻重无关

（B）伽利略认为物体越重，下落得越快

（C）牛顿管实验说明没有空气阻力时，铁块和羽毛下落快慢相同

（D）石头下落比树叶快，是因为树叶受到空气阻力，而石头没有受到空气阻力

【答案】

C

【解析】

亚里士多德认为物体越重，下落越快，而伽利略认为物体下落快慢与物重无关，通过牛顿管实验证明，无空气阻力时，铁块与羽毛下落快慢相同，在实际中虽然石头下落比树叶下落快，但石头仍受阻力，只不过其阻力相对其重力较小。故C正确，A、B、D错。

 

76．关于自由落体运动，下列说法正确的是（    ）

（A）自由落体运动的物体初速度为零

（B）物体从静止开始，竖直下落的运动就是自由落体运动

（C）自由落体运动的物体只受重力作用

（D）自由落体运动是变加速直线运动

【答案】

AC

 

77．关于自由落体加速度g，下列说法正确的是（     ）

（A）重的物体的g值大

（B）g值在任何地方都一样大

（C）g值在赤道处大于南北两极处

（D）同一地点轻重物体的g值一样大

【答案】

D

 

78．一物体做自由落体运动。从下落开始计时，重力加速度g取10 m/s²。则物体在第5 s内的位移为（     ）

（A）10 m           （B）125 m          （C）45 m            （D）80 m

【答案】

C

 

79．某人在高层楼房的阳台外侧边以 30 m/s 的初速度竖直上抛一个石块，空气阻力不计，石块运动到离抛出点 25 m 处所经历的时间可能是（       ）

（A）1 s    （B）3 s    （C）5 s    （D）（3＋\(\sqrt 14 \)）s

【答案】

ACD

【解析】

石块运动到离抛出点25 m处包括两种情况：一种是在抛出点上方25 m处，h＝25 m，一种是在抛出点下方25 m处，h＝－25 m，由h＝v₀t－\(\frac{1}{2}\)gt²可知A、C、D正确。

 

80．设宇航员在某行星上从高32 m处自由释放一重物，测得在下落最后1 s内所通过的距离为14 m，则重物下落的时间是多少？该星球表面的重力加速度为多大？

【答案】

4 s，4 m/s

 

81．如图所示，小球从竖直砖墙某位置静止释放，用频闪照相机在同一底片上多次曝光，得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置，连续两次曝光的时间间隔均为T，每块砖的厚度为d。根据图中的信息，下列判断正确的是（     ）

（A）位置“1”是小球释放的初始位置

（B）小球做匀加速直线运动

（C）小球下落的加速度为\(\frac{d}{{{T^2}}}\)

（D）小球在位置“3”的速度为\(\frac{{7d}}{{2T}}\)

【答案】

BCD

【解析】

由题图可以知道每两个相邻的点之间的距离差是一样的，由Δx＝at²可知，a＝\(\frac{{\Delta x}}{{{T^2}}}\)＝\(\frac{d}{{{T^2}}}\)，所以B、C正确。点3的瞬时速度的大小为2、4之间的平均速度的大小，所以v₃＝\(\frac{{{x_{24}}}}{{2T}}\)＝\(\frac{{7d}}{{2T}}\)，D正确．由于v₃＝v₁＋a·2T，故v₁＝v₃－2aT＝\(\frac{{7d}}{{2T}}\)－2×\(\frac{d}{{{T^2}}}\)×T＝\(\frac{{3d}}{{2T}}\)，故A错误。

 

82．甲、乙两球从同一高度相隔1 s先后自由落下，在下落过程中（    ）

（A）两球的距离始终不变

（B）两球的距离越来越大

（C）两球的速度差始终不变

（D）两球的速度差越来越大

【答案】

BC

 

83．小球从空中h＝20 m处自由下落，与水平地面碰撞后以碰前速度的60%竖直反弹到某一高度。取g＝10 m/s²，不计空气阻力。求：

（1）反弹的高度是多少？

（2）从开始下落到第二次落地，经过多长时间？

【答案】

（1）7.2 m

（2）4.4 s

 

84．气球以5 m/s的速度从地面匀速上升，上升过程中从气球上掉落一个小物体，该物体离开气球后经2 s着地。小物体离开气球后，气球以1 m/s²的加速度匀加速上升。空气对小物体的阻力不计，g取10 m/s²。试求 ：

（1）小物体离开气球时，气球的高度；

（2）小物体着地时的速度大小；

（3）小物体着地时，气球的高度。

【答案】

（1）10 m

（2）15 m/s

（3）22 m

【解析】

（1）设小物体离开气球时，气球离地的高度为h，则

－h＝v₀t－\(\frac{1}{2}\)gt²（取向上为正方向）

所以h＝10 m

（2）小物体着地时的速度大小为

v_t＝v₀－gt＝－15 m/s（“－”表示方向向下）

（3）小物体 着地时，气球的高度

H＝h＋v₀t+\(\frac{1}{2}\)gt²＝22 m

 

85．如图所示，一小物块从静止沿斜面以恒定的加速度下滑，依次通过A、B、C三点，已知AB＝12 m，AC＝32 m，小物块通过AB、BC所用的时间均为2 s，求：

（1）小物块下滑时的加速度；

（2）小物块通过A、B、C三点时的速度分别是多少？

【答案】

（1）2 m/s²

（2）4 m/s，8 m/s，12 m/s

【解析】

法一：（1）设物块下滑的加速度为a，则x_BC－x_AB＝at²，所以a＝\(\frac{{{x_{BC}} - {x_{AB}}}}{{{T^2}}}\)＝\(\frac{{20 - 12}}{{{2^2}}}\) m/s²＝2 m/s².

（2）v_B＝\(\frac{{{x_{AC}}}}{{2T}}\)＝\(\frac{{32}}{{2 \times 2}}\) m/s＝8 m/s

由v＝v₀＋at得v_A＝v_B－at＝（8－2×2） m/s＝4 m/s

v_C＝v_B＋at＝（8＋2×2） m/s＝12 m/s.

法二：由x＝v₀t＋\(\frac{1}{2}\)at²知

AB段：12＝v_A×2＋\(\frac{1}{2}\)a×2²①

AC段：32＝v_A×4＋\(\frac{1}{2}\)a×4²②

①②联立得v_A＝4 m/s，a＝2 m/s²

所以v_B＝v_A＋at＝8 m/s，v_C＝v_A＋a·2t＝12 m/s.

法三：v_B＝\(\frac{{{x_{AC}}}}{{2T}}\)＝8 m/s，由x_BC＝v_Bt＋\(\frac{1}{2}\)at²

即20＝8×2＋\(\frac{1}{2}\)a×2²，得a＝2 m/s²

由v＝v₀＋at知v_A＝v_B－at＝4 m/s，v_C＝v_B＋at＝12 m/s.

 

86． 在某地地震发生后的几天，通向灾区的公路非常难行，一辆救灾汽车由静止开始做匀变速直线运动，刚运动了8 s，由于前方突然有巨石滚在路中央，所以又紧急刹车，经4 s停在巨石前。则关于汽车的运动情况，下列说法正确的是（    ）

（A）加速、减速中的加速度大小之比a₁∶a₂＝1∶2

（B）加速、减速中的加速度大小之比a₁∶a₂＝2∶1

（C）加速、减速中的平均速度之比\({\bar v_1}\)∶\({\bar v_2}\)＝2∶1

（D）加速、减速中的位移之比x₁∶x₂＝1∶1

【答案】

A

 

87．在水平直轨道上距离A点右侧10 m处，一辆小车以4 m/s的速度匀速向右行驶，5 s末，小车的速度立即变为2 m/s匀速向左行驶。设小车做直线运动的位移和运动方向都以水平向左为正方向，

（1）试作出小车在20 s内的v-t图象和x-t图象（写出必要的计算过程，以小车出发点为位移坐标原点）；

（2）根据图象确定小车在20 s末的位置。（用文字表达）

【答案】

（1）如图

（2）处于水平轨道的A点

【解析】

在前5 s内小车运动的位移x₁＝v₁t＝（－4）×5 m＝－20 m，方向水平向右；在后15 s内小车运动的位移x₂＝v₂t₂＝2×15 m＝30 m，方向水平向左；以小车的出发点作为坐标原点，在这20 s内小车的x-t图象和v-t图象如图

由图可知小车在这20 s内的位移x＝10 m，方向水平向左，即第20 s末小车处于水平轨道的A点。

 

88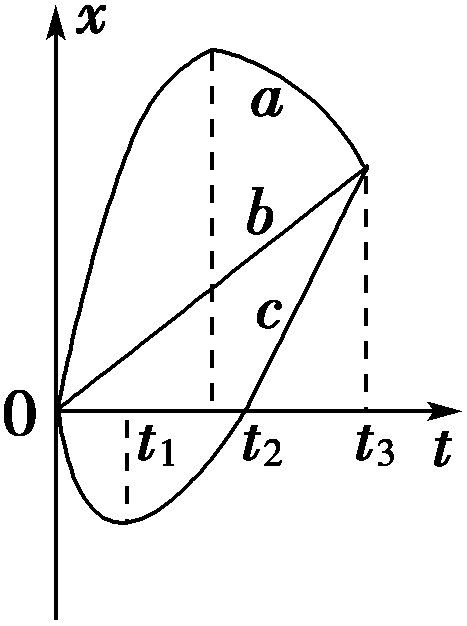．a、b、c三个质点在一条直线上运动，它们的位移-时间图象如图所示，下列说法正确的是（     ）

（A）在0～t₃时间内，三个质点位移相同

（B）在0～t₃时间内，质点c的路程比质点b的路程大

（C）质点a在时刻t₂改变运动方向，质点c在时刻t₁改变运动方向

（D）在t₂～t₃这段时间内，三个质点运动方向相同

【答案】

ABC

【解析】

0～t₃时间内三个质点的初、末位置均相同，但a、c两质点在运动过程中均改变了运动方向，质点a在t₂时刻改变运动方向，质点c在时刻t₁改变了运动方向，质点b的运动方向一直不变，故A、B、C均正确；t₂～t₃时间内，质点a沿－x方向运动，质点b、c均沿＋x方向运动，D错误。

 

89．甲车以加速度3 m/s²由静止开始做匀加速直线运动。乙车落后2 s在同一地点由静止开始，以加速度6 m/s²做匀加速直线运动。两车的运动方向相同，求 ：

（1）在乙车追上甲车之前，两车距离的最大值是多少？

（2）乙车出发后经多长时间可追上甲车？此时它们离出发点多远？

【答案】

（1）12 m

（2）（2＋2\(\sqrt 2 \)） s，70 m

【解析】

（1）两车距离最大时速度相等，设此时乙车已开动t秒，则甲、乙两车的速度分别是

v₁＝3×（t＋2） m/s，v₂＝6×t m/s＝6t m/s，

由v₁＝v₂得：t＝2 s，由x＝\(\frac{1}{2}\)at²知，两车距离的最大值

Δx＝\(\frac{1}{2}\)a_甲（t＋2）²－\(\frac{1}{2}\)a_乙t²

＝\(\frac{1}{2}\)×3×4² m－\(\frac{1}{2}\)×6×2² m

＝12 m

（2）设乙车出发后经t′秒追上甲车，则

x₁＝\(\frac{1}{2}\)a_甲（t′＋2）²＝\(\frac{1}{2}\)×3×（t′＋2）² m，

x₂＝\(\frac{1}{2}\)a_乙t′²＝\(\frac{1}{2}\)×6×t′²m

由x₁＝x₂代入数据，

求得t′＝（2＋2\(\sqrt 2 \)）s

将所求得时间代入位移公式可得x₁＝x₂≈70 m

 

90．如图所示，一辆长为13 m的客车沿平直公路以10 m/s的速度匀速向西行驶，一辆长为18 m的货车由静止开始以2.0 m/s²的加速度由西向东匀加速行驶，已知货车刚起动时两车车头相距200 m，求：

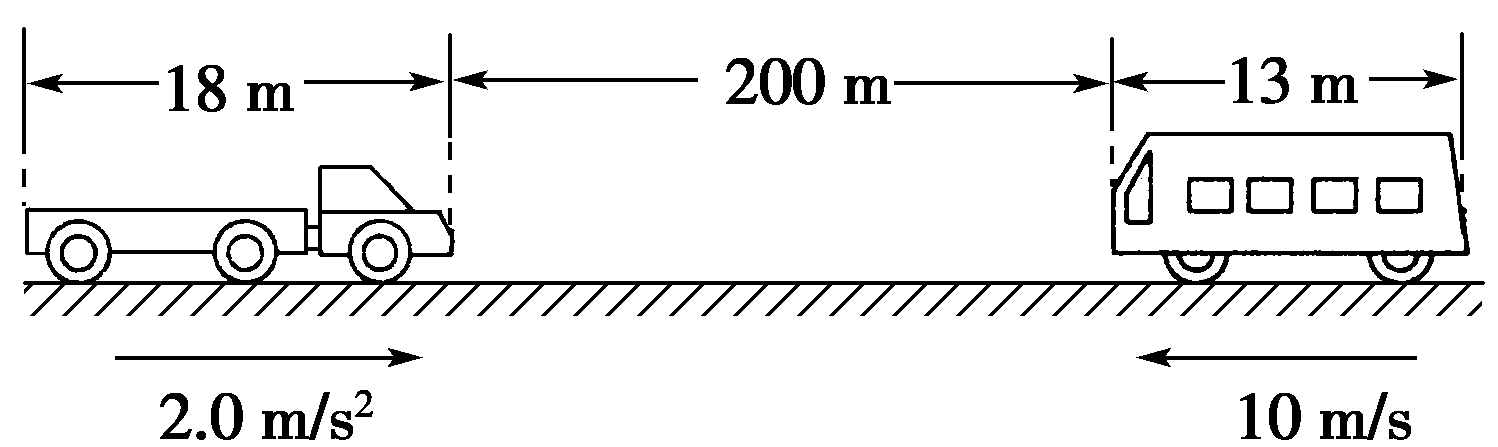
（1）货车起动后经多长时间两车车头相遇？

（2）两车错车（即车头相遇到车尾刚好分开）所用的时间。

【答案】

（1）10 s

（2）1 s

【解析】

（1）设货车起动后经过时间t₁两车相遇，此时货车的位移s₁＝\(\frac{1}{2}\)at₁²，客车的位移s₂＝vt₁，且有s₂＋s₁＝200 m，解得：t₁＝10 s

（2）设货车从开始起动到错车结束所用的时间为t₂，此时货车的位移s₃＝\[\frac{1}{2}\]at₂²，客车的位移s₄＝vt₂，且有s₃＋s₄＝231 m，

解得t₂＝11 s，

所以两车错车的时间为Δt＝t₂－t₁＝1 s

 

91．在做“探究小车速度随时间变化的规律”的实验中，取一段如图所示的纸带研究其运动情况。设O点为计数的起始点，在四个连续的计数点中，相邻计数点间的时间间隔为0.1 s，若物体做理想的匀加速直线运动，则计数点“A”与起始点O之间的距离x₁为________ cm，打计数点“A”时物体的瞬时速度为________ m/s，物体的加速度为________ m/s²。

【答案】

4.00，0.50，2.00

 

92．在做“探究小车速度随时间变化的规律”的实验时，所用交流电源频率为50 Hz，取下一段纸带研究，如图所示，设0点为计数点的起点，每5个点取一个计数点，则第1个计数点与起始点间的距离x₁＝______cm，计算此纸带的加速度大小a＝______m/s²；经过第3个计数点的瞬时速度v₃＝______m/s。

【答案】

3，3，1.05

 

93．物体做匀变速直线运动，已知在时间t内通过的位移为x，则以下说法正确的是（    ）

（A）可求出物体在时间t内的平均速度

（B）可求出物体的加速度

（C）可求出物体在这段时间内中间时刻的瞬时速度

（D）可求出物体通过\(\frac{x}{2}\)时的速度

【答案】

AC

【解析】

已知在时间t内的位移为x，可求出平均速度\(\bar v\)＝\(\frac{x}{t}\)，但不能求出加速度，A正确，B错误；做匀变速直线运动的物体在一段时间内的平均速度等于这段时间中间时刻的瞬时速度，C正确，D错误。

 

94．物体从静止开始做匀加速直线运动，第3 s内通过的位移是3 m，则（     ）

（A）第3 s内的平均速度是3 m/s

（B）物体的加速度是1.2 m/s²

（C）前3 s内的位移是6 m

（D）3 s末的速度是3.6 m/s

【答案】

ABD

 

95．物体做匀加速直线运动，在时间T内通过位移x₁到达A点，接着在时间T内又通过位移x₂到达B点，则物体（    ）

（A）在A点的速度大小为\(\frac{{{x_1} + {x_2}}}{{2T}}\)

（B）在B点的速度大小为\(\frac{{3{x_2} + {x_1}}}{{2T}}\)

（C）运动的加速度为\(\frac{{2{x_1}}}{{{T^2}}}\)

（D）运动的加速度为\(\frac{{{x_1} + {x_2}}}{{{T^2}}}\)

【答案】

A

 

96．甲、乙两物体做自由落体运动，已知甲物体重是乙物体重的2倍，而甲距地面的高度是乙距地面高度的一半，下列说法正确的是（     ）

（A）甲物体的加速度是乙物体加速度的2倍

（B）甲物体着地的速度是乙物体着地的速度的\(\frac{1}{2}\)

（C）甲物体下落的时间是乙物体下落的时间的\(\frac{{\sqrt 2 }}{2}\)

（D）甲、乙两物体的末速度相同

【答案】

C

 

97．两个质点A、B放在同一水平面上，由静止开始从同一位置沿相同方向同时开始做直线运动，其运动的v－t图象如图所示．对A、B运动情况的分析，下列结论正确的是（     ）

（A）A、B加速时的加速度大小之比为2∶1，A、B减速时的加速度大小之比为1∶1

（B）在t＝3t₀时刻，A、B相距最远

（C）在t＝5t₀时刻，A、B相距最远

（D）在t＝6t₀时刻，A、B相遇

【答案】

D

【解析】

由v－t图象，通过斜率可计算加速度大小，加速时A、B的加速度大小之比10∶1，减速时A、B的加速度大小之比为1∶1，所以选项A错误；由A、B运动关系可知，当A、B速度相同时距离最远，所以选项B、C错误；由题意可知A、B是从同一位置同时开始运动的，由速度-时间图象可以算出运动位移，可知6t₀时刻，A、B位移相同，因此在此时刻A、B相遇，所以选项D正确。

 

98．用接在50 Hz交流电源上的打点计时器测定小车做匀加速直线运动的加速度，得到如图5所示的一条纸带，从比较清晰的点开始起，取若干个计数点，分别标上0、1、2、3…（每相邻的两个计数点间有4个打印点未标出），量得0与1两点间的距离x₁＝30 mm，3与4两点间的距离x₄＝48 mm，则小车的加速度为________ m/s²，2与3两点间的距离约为________ mm，打计数点3时的瞬时速度为________m/s。

【答案】

0.6，42，0.45

 

99．在“探究小车速度随时间变化的规律”的实验中，电火花打点计时器使用的交流电源频率为50 Hz，记录小车运动的纸带如图所示，在纸带上选择标为0～6的计数点，相邻两个计数点间还有四个计时点未画出，纸带旁边并排放着毫米刻度尺，零刻度点跟0计数点对齐。

（1）请你根据放大的图片计算出打2和4两个计数点时的速度v₂＝________m/s、v₄＝________m/s（均保留2位有效数字），已知v₁＝0.1 5 m/s，v₃＝0.22 m/s，v₅＝0.39 m/s，请根据数据在图乙上作v-t图。

（2）电源频率低于50 Hz时，若仍按照50 Hz计算，则测出的速度值将比真实值________。（选填“大”或者“小”）

【答案】

在“探究小车速度随时间变化的规律”的实验中，电火花打点计时器使用的交流电源频率为50 Hz，记录小车运动的纸带如图所示，在纸带上选择标为0～6的计数点，相邻两个计数点间还有四个计时点未画出，纸带旁边并排放着毫米刻度尺，零刻度点跟0计数点对齐。

（1）请你根据放大的图片计算出打2和4两个计数点时的速度v₂＝________m/s、v₄＝________m/s（均保留2位有效数字），已知v₁＝0.1 5 m/s，v₃＝0.22 m/s，v₅＝0.39 m/s，请根据数据在图乙上作v-t图。

（2）电源频率低于50 Hz时，若仍按照50 Hz计算，则测出的速度值将比真实值________。（选填“大”或者“小”）

 

100．一枚小火箭携带试验炸弹竖直发射升空，小火箭的加速度a＝10 m/s²，t₁＝20 s后小火箭与试验炸弹分离，预定试验炸弹在最高点爆炸，取g＝10 m/s²，不计空气阻力。

（1）试验炸弹预定爆炸点的高度是多少？

（2）若试验失败，炸弹未爆炸，如果不采取措施，炸弹会在分离后多长时间落地？为了防止危险，在炸弹到达最高点10 s后，以v₀＝400 m/s竖直发射一枚炮弹拦截，拦截点的高度是多少？

【答案】

（1）4 000 m

（2）20（\(\sqrt 2 \)＋1） s，2 555 m